基于时间序列聚类方法的小长假铁路客流规律研究

王炜炜，单杏花

（中国铁道科学研究院 电子计算技术研究所，北京 100081）

基于时间序列聚类方法的小长假铁路客流规律研究

王炜炜，单杏花

（中国铁道科学研究院 电子计算技术研究所，北京 100081）

分析了小长假铁路客流的行成原因，从出行者特征和出行目的两方面总结了客流影响因素。以客票历史数据为依据，从日发送量、乘车里程等级、席别等级等方面分析了小长假铁路客流波动趋势。定义小长假客流波动系数，根据小长假客流的变化趋势特点，提出用基于波动趋势的客流时间序列聚类方法进行小长假客流规律的研究。并对聚类过程中小长假时间序列的构建、表示方法、特征值提取及聚类步骤进行了详细描述。

时间序列；聚类；小长假；客流波动

随着2008年国家节假日改革以来，小长假的次数增多，为人们提供了更多的出行机会，从而形成客流高峰。这就需要对小长假客流波动特征进行研究分析，从而准确预测客流，更好地指导运输组织方案优化以及客票预分。

文献[1]～[2]以客票数据为基础，绘制客流时间序列图，对客流周期性、趋势性进行了分析；文献[3]～[4]利用客票历史数据并通过市场调查，对京津线和京沪线旅客的出行结构、出行时间及特征进行了系统分析；文献[5]采用谱分析方法对南昌站春运40天客流波动进行了周期性分析。

目前铁路客流研究大部分集中在年度总量和春运客流上，而对于小长假期间客流的研究较少，本文研究内容主要面向节假日改革以来的小长假，主要包括“元旦”、“清明”、“五一”、“端午”、“中秋”5个假日。如无特别说明，下文所提小长假均指“3天”小长假。

1 小长假铁路客流特点分析

1.1 小长假铁路客流形成原因和影响因素

1.1.1 小长假铁路客流形成原因

在小长假期间，旅客根据需要选用铁路运输方式，在一定的空间范围内做有目的的移动便形成了铁路小长假客流。近年来，随着经济不断发展，人民对生活质量的要求不断提高，外出旅游已经被越来越多的人所接受。

通过对历史客流状况分析，对客流形成原因归纳总结如下：在出行者心理和生理方面，小长假外出或旅游或探亲，可以让人从工作中解脱出来，缓解压力；在经济基础方面，人们的生活水平提高，为小长假外出提供了经济基础，很大程度上增加了出行次数；在传统文化和社会生活方面，如清明节扫墓等传统文化习俗，促成了小长假期间客流高峰的形成；在国家政策方面，节假日改革以来的多个3天假期，为出行提供了相对充足的时间；在目的地资源方面，不同地区传统文化、旅游景点、气候变化、教育等资源都不尽相同，要体验不同的文化，出行必不可少。

1.1.2 小长假铁路客流影响因素

一般情况下，节假日期间，影响铁路客流的主要因素有：出行者特性因素、出行目的、出行距离、假期时间长短、城市类型等。

出行者个性因素对客流有很大的影响。不同的出行者在家庭背景、教育程度、职业收入等方面有很大差异，这也决定了他们在出行动机、出行选择、出行频次上的差异。其次，出行目的对客流有直接影响。一般在小长假期间，出行者目的大部分都是以聚会、旅游、购物等为目的的私人旅游，如图1所示。不同的小长假对客流的影响不同，这与假期性质、出行目的有直接关系。

图1 节假日铁路客流的形成示意图

出行距离对客流也会产生一定的影响。在3天小长假期间，由于时间局限性，选择长距离外出的旅客相对较少，而选择中、短距离出行的出行者是客流构成的主力。因此，中、短途出行对3天小长假客流影响较大。

综上所述，在小长假期间，出行者特性、出行目的、出行距离都将会影响到客流的变化。此外，城市类型也会影响到出行客流。因本论文选择的均为3天假期，由北京出发的所有客流，因而将不再把假期时间长度及城市类型作为分析考虑的因素。

1.2 小长假铁路客流数据统计分析

1.2.1 数据准备

本文所研究的小长假主要针对3天小长假，即“元旦”、“清明”、“五一”、“端午”、“中秋”5个节日。由上文分析得知，现行小长假自2008年施行以来，放假时间安排表如表1所示。

表1 小长假假期时间安排

由于2009年与2012年中秋节跟国庆节相遇，2014年元旦为周三，根据国家政策并不调休。因此本文选取2008年、2010年、2011年、2013年为研究样本年份。本文选择北京地区（包括北京站、北京西站、北京南站，北京北站，北京东站）的旅客发送数量为研究对象，研究小长假期间，其发出的所有列车的车票数据。研究时间段为各小长假期间及前后一周的客运数据。

根据以上分析，将客票历史数据进行整理、筛选、汇总，建立相应的数据库，以便分析使用。

图2 “五一”期间旅客发送量

1.2.2 日发送量统计分析

本文研究通过对客票历史数据整理，得到了各小长假在研究时段内北京地区的日发送量变化趋势。图2、图3为 “五一”和“端午”客流趋势图。其中Fn（n=1，2，…，7）表示假日前第n天，如“元旦”客流趋势图中的F7表示为“元旦”往前第7天的旅客发送量。

分析各小长假历年发送量数据，可以得到以下规律：

（1）旅客发送量自2008年始，有逐年上升趋势；

（2）节前数据分析。小长假开始前3天发送量开始上升，前2天客流开始明显上升，在小长假前一天客流达到峰值，小长假当天客流为最低值；

（3）节后数据分析。小长假假期最后1天发送量上升，节后第1天开始急剧下降，节后第2天开始缓慢下降，第3天基本稳定，直至回到小长假前的日发送量水平。

图3 “端午”期间旅客发送量

1.2.3 按乘车里程等级分析

对研究样本数据进行分析，得到研究时间段内最大发送里程为4 064 km，以100 km为里程间距，即乘车里程大于0并且小于等于100为第1个距离等级，以此类推，选取2013年“五一”小长假及其前后一周为研究时间段，得到不同距离等级的发送人数变化趋势图。分析数据发现里程大于1 500 km的发送量在小长假前后相差较小，4月22日～ 4月26日，5月3日 ～ 5月8日期间旅客发送量基本没有变化，因此选择100 km～1 500 km范围内，4月26日～5月3日之间的发送量，进一步研究分析，得到按乘车距离旅客发送量变化趋势如图4所示。

图4 按乘车距离旅客发送量

分析图4变化趋势，可以得到以下规律：

（1）在日期范围的每一天内，里程等级大于1 300 km（含1 300 km）的客流量随里程数的增加，客流量减少；在每个节假日的日客流量变化曲线中，里程等级为1 000 km的客流量既小于800 km的客流量，又小于1 300 km的客流量。

（2）里程等级为200 km的旅客数量最大，次之是里程等级为500 km和1 300 km的客流量。

（3）里程等级为200 km和500 km时，节假日第1天的日客流量均高于其他的日客流量；而里程等级为1 300 km时，客流量在小长假前1天达到最大值。

1.2.4 按席别等级分析

样本数据包含有14种不同席别，其中包厢硬卧、一人软包、混编软卧、混编硬座4种席别日发送量最大不超过100，略去不做分析，以2011年为研究对象，得到“清明”和“端午”分席别发送量变化趋势如图5和图6所示。

图5 “清明”期间分席别旅客发送量

图6 “端午”期间分席别旅客发送量

分析各小长假分席别发送量变化趋势得到以下规律：

（1）小长假席别变化趋势最大的是无座，这说明小长假运能不足；其次是动车二等座与硬座，变化最小的是硬卧，其他席别无明显变化。

（2）对于变化明显的席别，变化趋势与总发送量基本一致：小长假最后1天发送量上升，节后第1天开始急剧下降，节后第2天开始缓慢下降，节后第3天基本平衡，直至回到小长假前的日发送量水平。

2 小长假客流时间序列的构建

2.1 小长假客流波动系数提出

目前，客流波动系数比较多的应用在对春运期间客流规律的研究中，而对小长假期间的研究甚少。本文研究将小长假客流波动系数定义为：在小长假期间，假期当天旅客发送量与全年非节假日期间旅客日均发送量之比，设α为小长假客流波动系数，则可表示为：

2.2 客流时间序列构建

通过上文分析得知，小长假对平日客流的影响周期是节前4天～节后3天，本文根据小长假期间每天的客流波动系数来构建时间序列，则小长假客流时间序列可表示为：

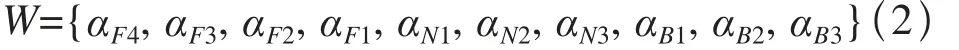
显然，小长假客流时间序列是一个步长较短的离散序列，序列中的每个对象都表示该点的波动系数，对象间的距离均为1，前后点的差表示变化趋势，整个序列体现了小长假期间的客流变化趋势。综上分析，本文考虑用差分来表示该序列的动态变化趋势。

2.3 客流变化趋势序列构建

由2.2小节分析，需要构建小长假客流动态变化趋势序列，该序列要求能表述客流时间序列内相邻两个元素之间的变化大小幅度。本文选择用差分方法，通过客流时间序列内相邻两个元素的差分来构建小长假客流动态变化趋势序列进行聚类分析。

依次计算出序列中任意相邻两天的差分值，并按照客流时间序列进行顺序组合，就得到了小长假客流变化趋势序列，如公式（4）。

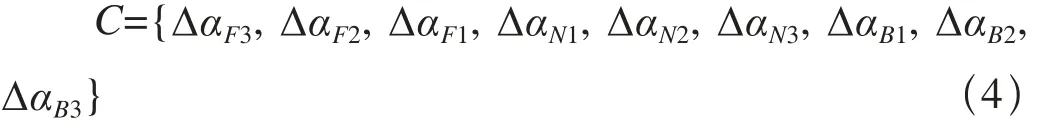
2.4 小长假客流时间序列的表示方法

本文选用逐段线性化方法来对小长假客流时间序列进行聚类分析，可以直观地反映时间序列的变化形态。

2.5 小长假客流时间序列的聚类

聚类的方法很多，系统聚类过程可形成聚类谱系图，便于观察。因此本文选取系统聚类来实现小长假客流时间序列聚类分析，步骤如下：

（1）确定聚类指标和建立样本矩阵

根据文分析，聚类指标确定如下：

设聚类指标为p，则有p=10，设样本数为 n，得到样本矩阵为：

（2）数据标准化

数据标准化方法众多，包括标准差、均差、协方差、极差等，本文选用Z-Score标准化方法，计算公式为：

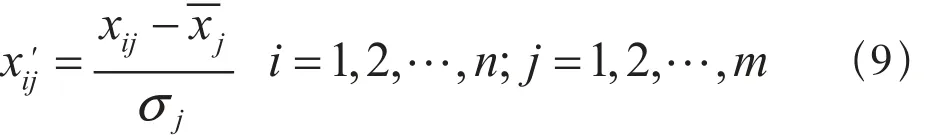
式（9）中：

（3）距离矩阵

序列的聚类可以转化为点聚类。本文以小长假时间序列作为样本，聚类指标为p=10, n个样本就组成了10维空间中的n个点。用表示两个样本间的距离，采用欧式距离作为聚类距离的度量，则表示为：

（4）选择聚类方法

本文选用离合平和方法作为层次聚类方法，即两类合并所产生的离差平方和的增量作为两类的距离。

（5）聚类结果的实现

聚类基本步骤为：

a.将n个时间序列各自编成1类，即将样本编为n类；

b.寻找n类中类间距离最小的两类，并将其合并为1类，则样本空间此时共有n–1类；

c.寻找n–1类中类间距离最小的两类，再次合并得到n–2类；

d. 重复以上过程，直到样本归为1类；最后生成聚类谱系图。

运用以上聚类分析方法，可以针对某城市、某条高速铁路或者某车站进行小长假客流波动规律的研究。将分析结果（如不同节假日每一类客流的波动系数变化特征及具有同类别客流波动特征的不同OD区间的相关资料、客流波动系数等）全部记录存库，建立一个客流波动规律数据库，用于后续的节假日客流预测和运输组织优化。

3 结束语

本文以3天小长假为研究对象分析了小长假铁路客流的形成因素和影响因素，基于客票历史数据，对不同小长假假日期间旅客发送量分别从总发送量、按乘车里程等级、按席别等级3个角度进行了分析对比，总结出小长假客流波动规律；定义了小长假客流波动系数，并提出用基于波动趋势的客流时间序列聚类方法来进行小长假客流规律研究的方法，最后给出了该方法的具体步骤。运用该方法得到的客流波动规律数据，对于节假日铁路客流预测、临客开行方案制定，具有重要指导意义。

[1] 马彦祥，高 篙.铁路短期客流时序规律分析[J].铁道运输与经济，2010，32（2）：87-90.

[2] 马彦祥.基于客流激发能级模型的铁路客流短期预测研究[D].北京：北京交通大学，2008.

[3] 张 敏，张 超.京津城际高速铁路客流结构和出行特征分析[J].中国储运，2010（6）：88-89.

[4] 甄 静.京沪线路客流规律分析[J].中国铁道科学，2002，23（2）：122-126.

[5] 廖智君.南吕客运站春运客流分析及对策研究[D].成都：西南交通大学，2003.

[6] 夏 青. 节假日铁路客流波动规律分析及其在客流预测中的应用研究[D].北京：北京交通大学 ，2011.

责任编辑 方 圆

Study on regular pattern of railway passener fl ow in three-daw holiday based on clustering method of time series

WANG Weiwei, SHAN Xinghua
( Institute of Computing Technologies, China Academy of Railway Sciences, Beijing 100081, China )

The paper analyzed the causes of the railway passenger flow in the three-day holiday, summarized the factors of the railway passenger flow from the characteristics about passengers and travel purposes, based on the historical tickets data, analyzed the fl uctuation characteristics of passenger fl ow in three-day holiday from transport volume, the grade of the board distance, the grade of the seat type, etc, def i ned the three-day holiday passenger fl ow fl uctuation coeff i cient and based on a small holiday passenger trends, proposed a clustering method of time series to study the regular pattern of passenger fl ow in the three-day holiday and made detailed descriptions about the building of time series of the three-day holiday and its representations, eigenvalue extraction and clustering step.

time series; clustering; three-day holiday; fl uctuation characteristics of passenger fl ow

U293.2∶TP39

A

1005-8451（2015）04-0023-05

2014-09-23

王炜炜，副研究员；单杏花 ，研究员。