GPS水准中三种曲面拟合模型的对比分析

崔卫磊(贵阳市测绘院,贵州贵阳 550002)

GPS水准中三种曲面拟合模型的对比分析

崔卫磊∗
(贵阳市测绘院,贵州贵阳 550002)

摘 要:在详细论述了GPS水准中平面相关、曲面样条、多面函数三种曲面拟合方法之上,编写了GPS高程拟合系统软件。最后利用四川省某地区的实测数据,对以上几种拟合方法进行比较和分析,得到了一些有用的结论,对类似测量项目有一定的借鉴意义。

关键词:GPS;水准;多面函数;平面相关;曲面样条;对比分析

1　引 言

GPS是近些年发展起来的先进导航定位技术,但在使用GPS进行控制测量时GPS的平面坐标可以达到毫米级,而高程精度却由于常常无法满足施工的需要而只能采取其他方法获取,这使得GPS测量技术的优势大打折扣。究其原因是GPS所测高程为以参考椭球面为基准的大地高,传统测量却是以似大地水准面为基准的正常高。因此寻求求解大地高于正常高之间的差异,即高程异常的方法就变得尤为重要。求解高程异常的方法有重力法、GPS水准法、GPS三角高程方法、联合平差法、转换参数法、神经网络法等方法。其中GPS水准方法是普遍,也是最容易实现的采用的一种方法。

2　GPS水准方法

GPS水准方法是眼下正常高的求取中最常用的一种方法,具体做法为:利用测区内已知高程异常的已知点,采用比较适宜的模型对该测区的似大地水准面进行拟合,然后求出待定点的高程异常值,进而确定整个测区的正常高。它的优点是算法相对来讲还算简单,不受中、长波项及高程系统差异等的影响,无须地球重力场方面的专门知识或数据。缺点是在山区精度会严重受损。

目前,比较常用的GPS水准方法除了绘等直线图法以外主要分为曲线拟合法和曲面拟合法。曲线拟合法主要有,多项式曲线、三次样条曲线、阿克玛法等方法。曲面拟合法有相关平面、斜平面、多项式曲面、多面函数、曲面样条、移动曲面等。本文将详细论述相关平面法,多面函数法以及曲面样条拟合法,并应用实测数据对这三种方法进行对比分析。

2.1平面相关拟合法

这种拟合法也称为四参数曲面拟合法。基本表达式为:

f(x,y)= a0+a1x+a2y+a3xy

此方程式的关键就是求未知参数ai(i = 0,1,2, 3),所需公共点最少为4个。此方法的适用条件为:地形起伏不大的地区,这些地区的似大地水准面非常的缓和,大致可以用一个平面表示。

2.2曲面样条拟合法

曲面样条拟合法与其他拟合法相比,具有以下优点:就用于曲面样条函数拟合的原始数据而言,它们不必按规则排列;采取自然边界条件而不需边界导数的信息,就可以得到任意阶可微的光滑曲面:拟合后的光滑曲面通过每个已知原始数据点;用于曲面拟合的原始数据点数≥3即可。下面介绍曲面样条函数的原理。

曲面样条拟合法是基于无限大平板小挠度方程的数学模型,设点的坐标x、y存在如下样条关系:

式中:

xi,yi为已知点的坐标,x、y为未知点的平面坐标。式(2)中,δ为平滑因子,一般取值为1。

由式(1)可知,当有m个已知的GPS水准联测点时,则有m+3个未知参数,即(α1,α2,α3,F1,F2,…, Fm),而方程的个数也为m+3个,因此求解此方程组求出这些参数。当GPS水准联测点有n个时,n＞m,可按最小二乘法求解这出这m+3个未知数,进而求出所有待定点的高程异常值。

对于式(1)的求解,最少要知道3个已知点。

2.3多面函数法

在用平面拟合法对测区进行拟合时,测区地形不能有太大的起伏,而且测区面积不能太大。如果想要得到精度较高的结果,除上述条件以外,还要求公共点分布均匀。一旦测区比增大,如果仅仅采用平面拟合法,效果就很不好。如果拿二次曲面和平面拟合法进行比较的话,二次曲面所得结果要比平面拟合法精度要高,但它也存在弊端。二次曲面为单峰曲面,无法描述整个测区。如果此时用多于两次的曲面拟合法进行拟合,则一方面需要更多的公共点,另一方面,曲面也容易发生抖动,其结果精度也不是很高。特别是当遇到带状分布,且跨区较长时,如果单纯地用一个面来表示,效果就很不好。此时,就可以考虑另外一种拟合方法,多面函数法。

1971年,美国的Hardy教授提出了多面函数拟合法。1976年,多面函数拟合法在测量领域开始逐步推广,多面函数最初的提出,是为了解决由数据点组成的数学曲面这方面的难题。它的基本思想为“任何一个圆滑的数学表面总是可以用一系列有规则的数学表面的总和,以任意的精度逼近”。具体步骤为,将每一个未知点,与全部的已知点分别建立函数关系,最终处理和叠加多面函数的值,将未知点给求出来。

设待定参数为βj;平面坐标的核函数设为F(x,y, xj,yj);多面函数的函数关系式如下:

常用的F(x,y,xj,yj)的函数式为:

上式中,δ2通常被称为光滑因子,它的取值为任意常数;k的取值有多种,通常k为±1/2。当k为1/2时为正双曲面函数,k=-1/2时为倒双曲面函数。

设有n个已知点(xi,yi)(i=1,2,…,n),选其中m (m≤n)个点(xj,yj)(j=1,2,…,m)为核函数的核心,并令Qij=F(xi,yi,xj,yj),则式(3)转变为:

由此可列误差方程式:

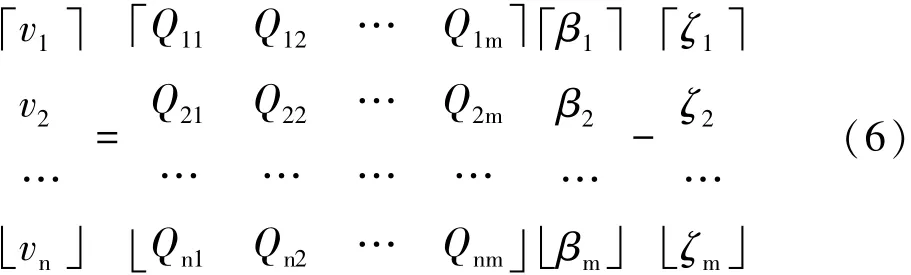
表示成向量的形式:

在最小二乘法的原则下,可求得:

从而求出多面函数的方程式。

多面函数法进行曲面拟合时,以下几个问题是难点:

(1)选用什么样的核函数。它是非常重要的,直接关系着最终结果的好和坏。通常情况下,都是取正双曲面函数,函数式如下:

F(x,y,xj,yj)= [(x-xj)2+(y-yj)2+δ2]1/2

(2)光滑因子的确定也是一个难点,它没有理论指导,只能不断进行尝试和改进。而由文献[4][8],光滑因子可以做如下尝试:

设x、y为已知点坐标,xi、yi为未知点的坐标,则任意两者之间的距离为:

dij=[(x-xi)2+(y-yi)2]

设已知点数据集为A,未知点的集合为B,两者之间距离的平方的集合为dij(A,B),则取δ=max{dij(A, B)}或更大时,一般都能够取得比较好的精度。

(3)如何选择核心点。多面函数的核心点有一定的要求,必须要高程异常显著,如测区的最高点或者最低点,或者是坡度变化处。

多而函数拟合法理论是非常严密的,但是具体实践起来却有一定的难度。

3　三种曲面拟合模型的对比分析

为了对GPS水准中三种曲面拟合模型进行分析,本文利用VB,并结合Matrix VB控件编制了GPS高程拟合系统软件。本软件主要的模块分为读入起算点、读入待拟合点、选择检核点、计算四部分。计算后文件小,操作方便。其中读入起算点是将所有已知点都要输入,而读入待拟合点是将需要进行拟合的数据点进行输入。选择检核点,是对拟合点和检核点进行区分的阶段。如图1、图2所示:

图1　高程拟合系统主界面

图2　高程拟合计算结果图

3.1数据来源

数据来源于四川省成都市下辖某地区控制网数据的一部分。该地区为成都市东部主城区,交通便利。所选的整个测区呈面状分布,暂将该地区命名为A测区,测区长约25 km,宽约8 km,总面积有160.4 km2,海拔在500 m左右,地势起伏不大,高差在50 m左右。整个测区共布设D级GPS控制点30个,并且全部用三等水准进行联测。每点的间距在6 km左右。

3.2方案1对比分析

方案1:以整个A测区为研究对象均匀选取12个控制点参加拟合,剩下的18个点作为检核点,分布图如图3所示,拟合点之间的点位间距平均在6 km左右。分别采用平面相关拟合法、多面函数法、曲面样条拟合法对测区控制点进行拟合。

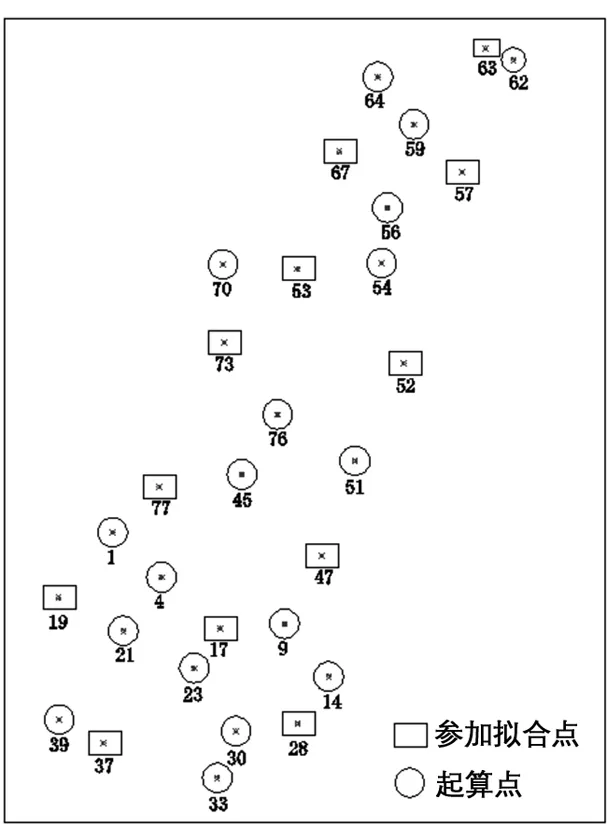
图3　方案1拟合点分布图

经过拟合,18个检核点采用三种拟合方法所得的拟合结果的残差图如图4所示,各个检核点的残差结果如表1所示。

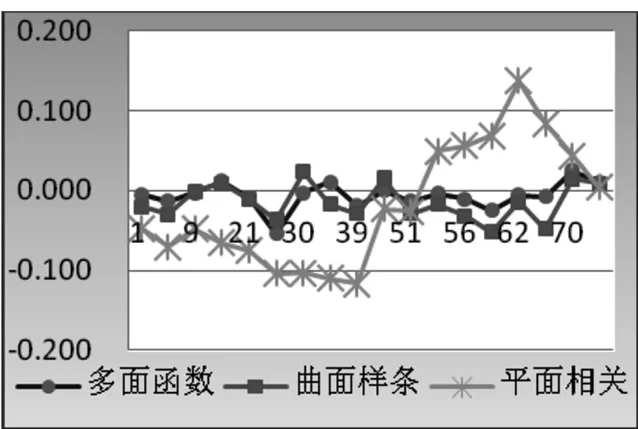
图4　方案1检核点残差图(单位/ m)

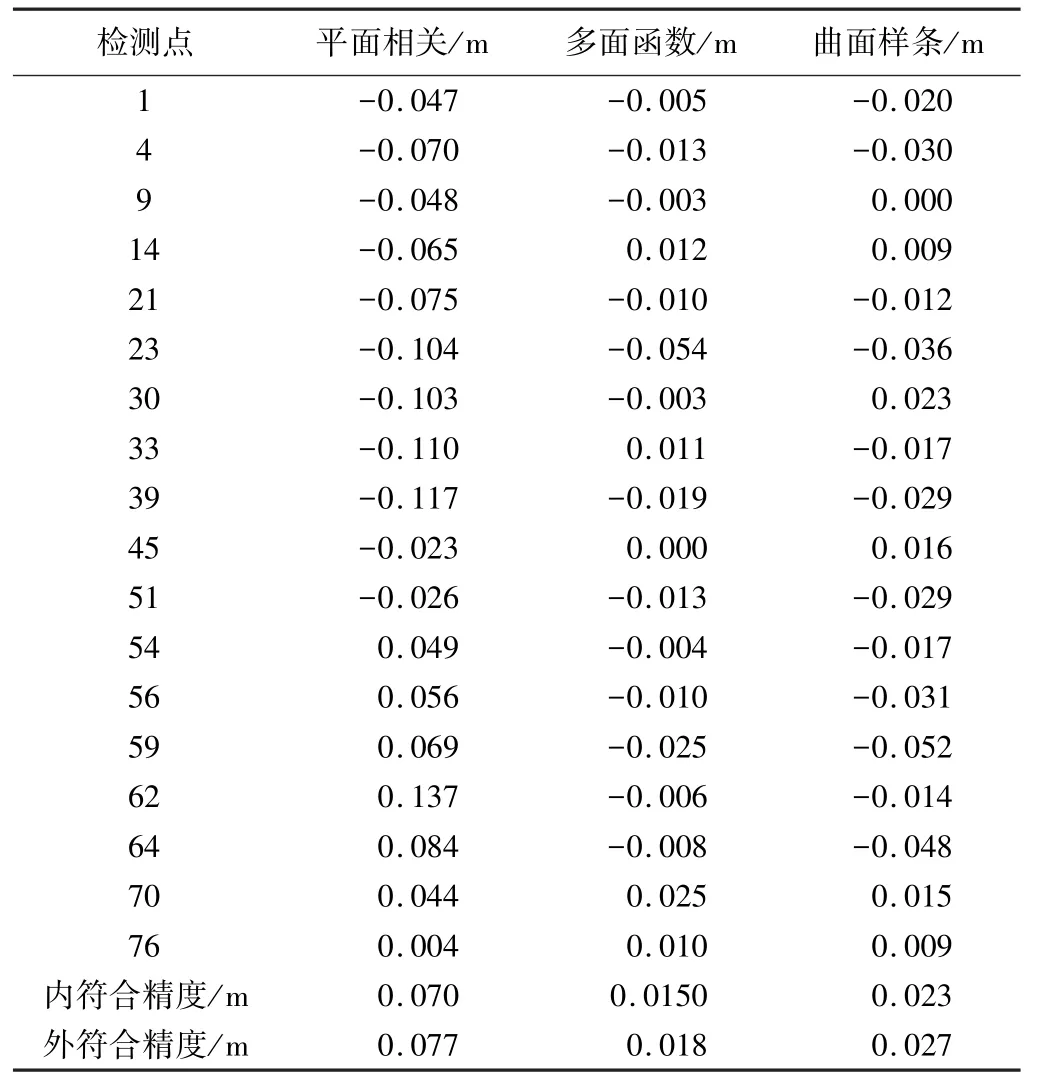
方案1检核点残差表 表1

由表1及图4可以看出:多面函数拟合法和曲面样条拟合法拟合精度比较高,平面相关拟合法精度比较低,三者中多面函数的精度最高。说明在地势比较起伏不大的地区, 160 km2以下的区域,只要控制点分布均匀合理,多面函数和曲面样条都可以满足精度要求,但平面相关拟合法在面积比较大的情况之下,所受影响比较大。

但是平面相关拟合法相比另外两种拟合方法来说,建模比较简单,程序更容易实现。因此做出以下探讨。缩小测区的范围,分别采用多面函数和平面相关进行拟合。

3.3方案2对比分析

方案2:从整个测区中选出一部分,命名为B测区,总体面积约有80 km2,所选测区总共30个点,选择7个进行拟合,其余23个进行检测,分布图如图5,采用平面相关法和多面函数法进行拟合。拟合结果的残差图如图6所示,各检核点的残差如表2所示。

由表2及图6可以看出:随着面积的减小(实验数据由160 km2变为80 km2,密度保持基本不变),平面相关拟合的精度有了很大提高(大部分小于0.4 cm),跟多面函数拟合出来的结果相差不是特别的大。因此可以说在精度要求不太高的测绘项目之中,在与实验地形条件类似的情况下,这种拟合方式可以应用。

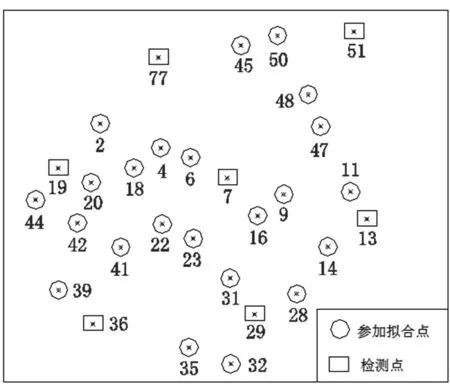
图5　方案2拟合点分布图

方案2检测点残差表 表2

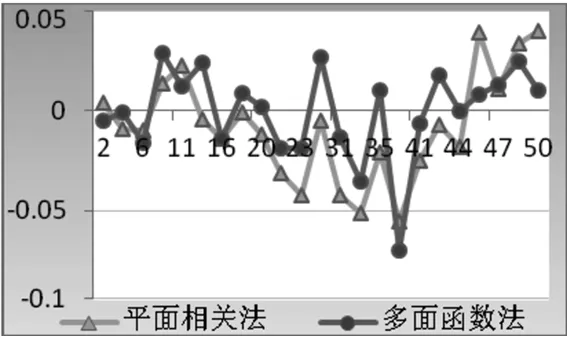
图6　方案2检测点残差图(单位/ m)

4　结 论

在测区起伏不大,且面积较小时,多面函数、平面相关法都能够达到比较好的拟合结果。但是随着测区面积的增大,平面相关拟合法效果要远低于多面函数和曲面样条拟合法,甚至达不到精度要求。对三种曲面拟合方法来讲,面积是一个比较重要的因素。但是面积对平面相关拟合法的影响要远远大于对多面函数和曲面样条拟合法的影响。

进行高程拟合时,如果能够选用合适的拟合模型,就能够达到满足施工需求的精度。但是这种高程点能够用于一般的施工控制测量,但是不能用于高等级的控制点。另外,在高程拟合的时候,为了便于发现错误,可以将拟合数据与实验数据互相检查。

参考文献

[1] 徐绍铨,张华海,杨志强等.GPS测量原理及应用[M].武汉:武汉测绘科技大学出版社,1998.

[2] 陶本藻.GPS水准似大地水准面拟合和正常高计算[J].测绘通报,1992(4).

[3] 李晓恒.GPS水准拟合模型的优选[J].测绘通报,2003 (7):11～13.

[4] 徐绍铨,李振洪,吴云孙.GPS高程拟合系统的研究[J].武汉测绘科技大学学报,1999(4):336～339.

[5] 赵生金,孙德厚.采用移动拟合法进行GPS网高程拟合的探讨[J].城市勘测,2007(2):23～25.

[6] 钟波,罗志才,呼旭.两种GPS水准综合模型的比较研究[J].测绘信息与工程,2007,32(2):14～16.

[7] 马洪宾,董仲宇.多面函数GPS水准高程拟合中光滑因子求定方法[J].东北大学学报·自然科学版,2008(8): 1176～1191.

[8] 崔卫磊.GPS高程拟合模型的研究及应用[D].成都理工大学,2013.

[9] 杨江波,李为乐,余代俊等.GPS高程拟合方法的实验研究[J].测绘科学,2009(5):54～56.

Comparison and Analysis on Three Kinds of Curved Surface Fitting Model of GPS Leveling

Cui Weilei
(Guiyang Surveying and Mapping Institute,Guiyang 550002,China)

Abstract:This paper discussed in detail three kinds of surface fitting method,that was plane related,surface spline, polyhedral function of GPS leveling,And then edited the software of GPS elevation fitting system.Finally,it used the actual data of a region of Sichuan Province by close comparison and analytic study obtaining some useful conclusions,what had some reference significance to similar measurement project.

Key words:GPS;leveling;plane related;surface spline;polyhedral function;comparative analysis

文章编号:1672-8262(2015)01-85-04中图分类号:P228

文献标识码:A

收稿日期:∗2014—10—12

作者简介:崔卫磊(1985—),男,硕士,主要从事测绘技术工作。