改进GM(1,1)在高铁隧道沉降变形预测中的对比应用

陈玲菊(玉环县城建测量队,浙江玉环 317600)

改进GM(1,1)在高铁隧道沉降变形预测中的对比应用

陈玲菊∗
(玉环县城建测量队,浙江玉环 317600)

摘 要:针对传统GM(1,1)模型在高铁隧道沉降变形分析与预测中精度不理想状况,本文在传统GM(1,1)模型基础上,建立自适应GM(1,1)模型与残差修正GM(1,1)模型并讨论两种改进模型各自优点。利用传统GM(1,1)模型、自适应GM(1,1)模型以及残差修正GM(1,1)模型对某高铁隧道监测点作沉降分析与预测。通过对比,得出自适应GM (1,1)模型与残差修正GM(1,1)模型对原模型的预测曲线相关性和预测精度有一定程度提高;残差修正GM(1,1)模型对于沉降曲线波动较大处仍有较好的拟合与预测效果,其预测效果优于自适应GM(1,1)模型。

关键词:传统GM(1,1);自适应GM(1,1);残差修正;高铁隧道;变形预测

1　引 言

高铁由于运行速度快,要求线路具有高平顺和稳定性,因而对沿线工程地质条件提出了很高要求,隧道作为其中一部分,其稳定性更显重要;但受自然或人为因素以及列车的高速运行及其震动等因素影响,高铁隧道不可避免会发生沉降变形。因此,对高铁隧道沉降进行有效监测是其运营维护的重要工作内容之一。然而其沉降变化存在较大的随机性和模糊性,所以沉降过程是一种灰色过程。灰色GM(1,1)模型[1]以其显著的优势被广泛应用于高速铁路隧道沉降变形评估与预测中,但由于模型的局限性,在应用过程中遇到了预测精度不理想的情况。为此,本文依据新建贵广高铁某隧道的沉降变形实测资料,改进传统灰色GM(1,1)模型,建立自适应GM(1,1)模型与残差修正GM(1,1)模型,并对原始沉降监测数据进行形变分析与预测结果的对比分析。

2　传统GM(1,1)模型

灰色系统就是指既含有未知的或非确知的又含有已知的信息系统[2]。它是通过对非确定或反映系统行为特征较少的信息作变换来建立灰色模型,借此来推导系统运行的实际行为和发展规律。GM(1,1)模型是只需一个适用于变形预测分析的灰色数列模型,其建立过程如下[2～5]:

设x(0)为某监测点各期等时间间隔监测非负初始数据序列:

式中n为序列长度,k=1,2,…,n。对初始序列进行一次性累加,则生成数列(记x(1)= AGOx(0)):

对式(2)中求时间偏导,建立GM(1,1)一阶线性灰微分方程,则可得到GM(1,1)模型的白化方程:

式中a用于控制系统发展态势大小,称为发展系数;b用于反映数据的变化关系,称为灰色作用量。对方程(3)求一重积分,得到GM(1,1)白化方程的时间响应式:通过累减生成GM(1,1)预测模型:

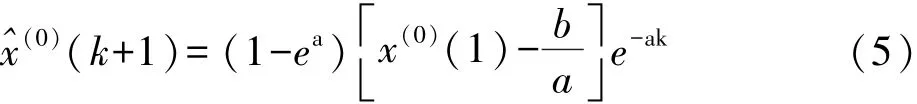
3　自适应GM(1,1)模型

传统GM(1,1)模型是采用现实状态t=n为止的过去数据进行建模的,一些随机干扰因素将随时间推移进入预测系统,对后期预测产生影响。针对此缺陷,为能准确预测隧道沉降状况,对变形量作动态分析,同时考虑t＞n的未来因素,即在GM(1,1)模型的原始序列中输送一系列新的数据,建立新的GM(1,1)预测模型。

自适应GM(1,1)模型的建模原理是依据初始序列x(0)= [x(0)(1),x(0)(2),…x(0)(n)]建立GM(1,1)模型,通过该模型可求得预测值x(0)(n+1),它是t=n+ 1时刻的变形预测值,将该预测值加入到初始序列,同时舍去初始序列中x(0)(1),得到新的数据序列x(0)1=[x(0)(2),x(0)(3),…x(0)(n+1)],并以此重新建立模型,这就是自适应GM(1,1)模型。

4　残差修正GM(1,1)模型

在传统GM(1,1)模型预测精度不符合要求时,可通过残差数列建立残差修正GM(1,1)模型[6],可使模型预测精度得到提高。设原模型的残差序列为:q(0)= {q(0)(1),q(0)(2),…,q(0)(n)},其中q(k)= x0(k)-^x0(k)。若存在k0满足∀k≥k0,q(0)(k)的符号一致且n -k0≥4,则称{ | q(0)(k0) |,| q(0)(k0+1) |,…,| q(0)(n) |}为可建模残差尾段;如果残差序列为异号时,需对数据进行平移处理,将残差序列转化为同号,建立残差GM(1,1)模型,最后做平移还原处理,修正原模型,建立残差修正GM(1,1)模型。

依据可建模残差尾段序列q(0)(k),建立GM(1,1)模型,结合GM(1,1)模型的时间响应式(4)与还原GM (1,1)预测模型式(5),最后可得残差GM(1,1)模型:

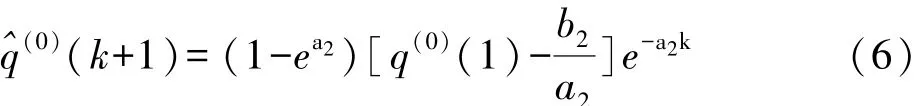
将残差GM(1,1)模型,式(6)加入原模型中可得残差修正GM(1,1)模型:2

5　模型精度评定

本文采用后验差检验法[7]判定模型的预测精度。设初始数据求得的方差为s21,由残差数据得到的方差为s22,其求解公式为:

小误差概率为:P=P{ |q(k)-q¯|＜0. 6745s1}后验差比值为:C=s2

s1

参考P和C两指标值,可对模型精度进行综合评定,其等级划分如表1所示。

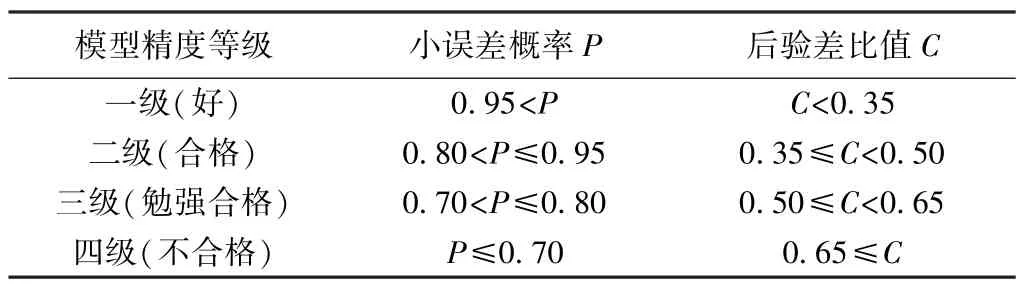
后验差检验法精度等级表 表1

6　实例分析

新建某高铁隧道的沉降变形监测,按二等水准要求,使用天宝DiNi03数字电子水准仪每7天进行一期观测。该实例利用某监测点连续13期监测观测数据,用自适应和残差修正两种GM(1,1)模型分析与预测其沉降变形。

首先利用前9期观测数据建立9维传统GM(1, 1)模型,然后预测后4期,结果如表2、图1所示;利用传统GM(1,1)模型的第1期预测值替换初始序列第10期数据建立自适应GM(1,1)模型,并舍去初始序列的第1期数据,构成新9维建模序列,再按传统GM (1,1)模型构建方法生成自适应GM(1,1)模型,依次循环,可得到后几期的预测值;依据传统GM(1,1)模型的残差序列,本文以后8期的残差序列建立残差修正GM(1,1)模型,由于残差序列异号,对其进平移处理,将残差序列转化为同号。

改进后两种模型与传统GM(1,1)模型的对比结果表2,图1,图2所示。

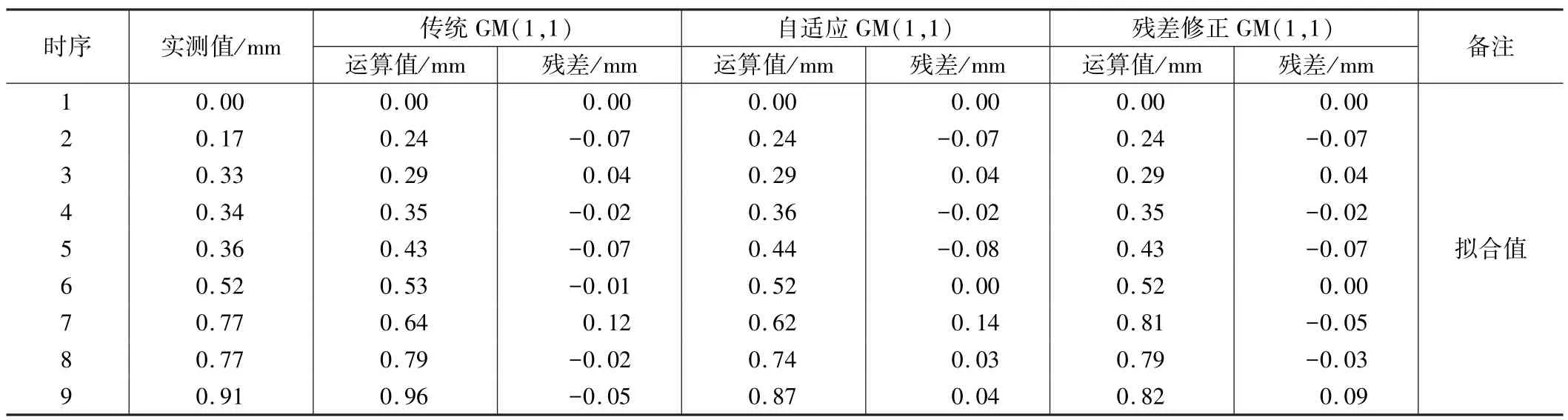
三种模型的预测值与实测值对比表 表2

续表2

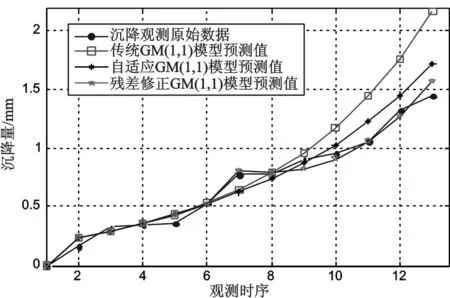
图1　原始值与三种模型预测值对比

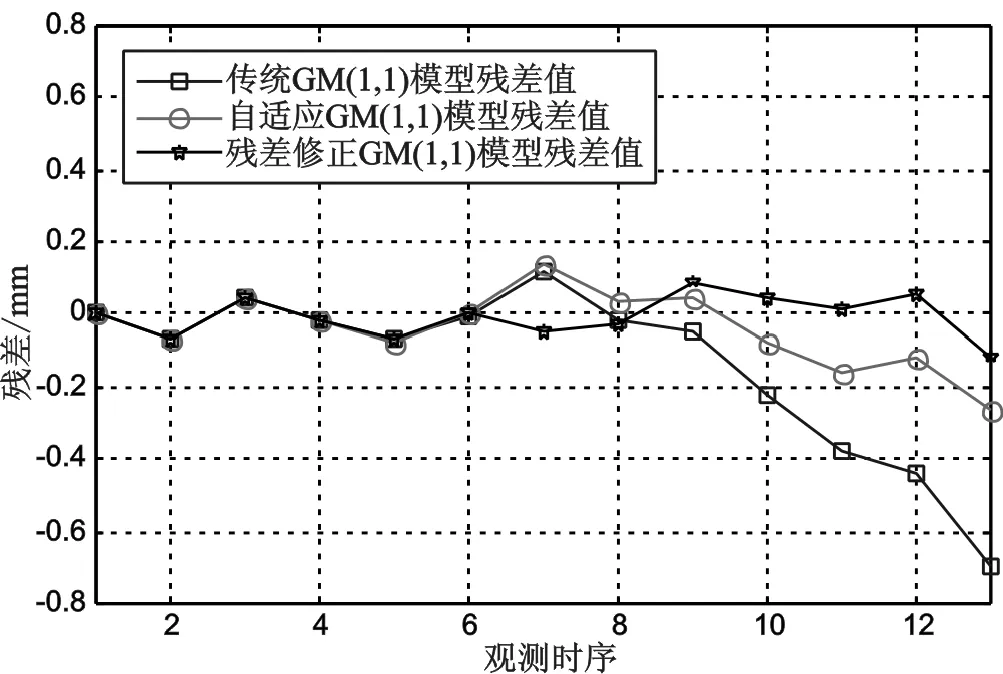
图2　模型残差曲线对比

通过以上图表可知,前6期三种模型的残差几乎一致,第6期以后传统GM(1,1)模型的残差随时间有递增趋势,且预测曲线逐渐偏离实测曲线;自适应GM (1,1)模型预测曲线与实测曲线较吻合,相对于传统GM(1,1)模型其预测精度有所提高;预测曲线与实测曲线几乎一致的是残差修正GM(1,1)模型,它较好地预测了后几期的变形量,且残差没有递增的趋势;实测曲线中第7期波动较大,残差修正GM(1,1)模型可以很好地修正原模型,使第7期的拟合值与实测值非常接近。

采用后验差检验法对以上三种模型进行精度评定,三种模型的综合精度等级、小误差概率P及后验差比值C如表3所示。

对三种模型的预测曲线进行线性相关性分析,结果如表4所示。

三种模型的模型精度比对表 表3

由表3、表4可知,改进后的GM(1,1)模型的精度等级均由二级提升到一级;较传统GM(1,1)模型,自适应GM(1,1)模型与残差修正GM(1,1)模型的预测曲线与实测沉降曲线的相关系数均有所提高,且残差修正GM(1,1)模型的相关系数最高。

7　结 论

针对高铁隧道沉降监测的分析与预测,本文采用实测数据,利用传统GM(1,1)模型和改进GM(1,1)模型对其进行分析与预测,通过对比分析,结论如下:

(1)在建模时,传统GM(1,1)模型保留了序列初期沉降信息,由于一些未来的噪声干扰随着时间的推移加入灰色系统,使得预测值随着时间推移越来越偏离实测值,这是因为传统GM(1,1)模型没有考虑未来噪声对预测的影响。

(2)自适应GM(1,1)模型由于能及时舍去建模序列中的初期信息,并不断加入近期实际信息,保证模型是一个递补动态预测模型,能及时有效修正模型误差,使预测精度得到提高。

(3)残差修正GM(1,1)模型对随机噪声进行了有用信息再次提取,起到精度补偿的作用,故该模型对于曲线波动较大处仍有较好的拟合与预测效果。

(4)改进的两种模型的预测精度均高于传统GM (1,1)模型,且三种模型中残差修正GM(1,1)模型的预测精度与准确度为最高。

参考文献

[1] 陈伟清,田海涛,陈佳佳.工程建筑物变形分析的灰色模型探讨[J].广西大学学报·自然科学版,2011,36(1): 64～70.

[2] 彭正明,王腾军,曹冬冬等.GM(1,1)模型的改进及其在变形预测中的应用[J].地球科学与环境学报,2012,34 (4):102～106.

[3] 何君,杨国东.灰色预测理论在建筑物沉降中的应用研究[J].测绘通报,2012(3):63～64.

[4] Erdal Kayacan,Baris Ulutas,Okyay Kaynak.Grey system theory-based models in time series prediction[J].Expert Systems with Applications,2010,37(2):1784～1789.

[5] 张清华,隋立芬,牟忠凯等.利用改进灰色模型的钟差预报算法及其精度分析[J].测绘科学,2012,37(1):51～53.

[6] 张健雄,蒋金豹,张建霞.高层建筑沉降监测与灰色预测[J].测绘科学,2007,32(4):56～59.

[7] 张军.灰色预测模型的改进及其应用[D].西安理工大学,2008.

[8] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉大学出版社,2009.

Comparison and Application of Improved GM(1,1) in High-speed Railway Tunnel Settlement Deformation Prediction

Chen Lingju
(Urban construction surveying group of YuHuan county,Yuhuan 317600,China)

Abstract:Aiming at the situation of the precision of traditional GM(1,1) in high-speed railway tunnel settlement deformation analysis and prediction is not ideal.This paper which is based on traditional GM(1,1) model has established self-adaptive GM(1,1) model and residual error correction GM(1,1) model and discussed their respective advantages.Using traditional GM (1,1) model, self-adaptive GM(1,1) model and residual error correction GM(1,1) model to analyze and predict a High-speed Rail tunnel monitoring points settlement deformation.Through comparing and analyzing, it is concluded that self-adaptive GM (1,1) model and residual error GM (1,1) model improve the prediction precision of original model and the correlation of prediction curve in a certain extent;residual error correction GM(1, 1) model has a better fitting and prediction effect for the settlement curve with bigger fluctuations, its prediction effect is superior to the self-adaptive GM (1, 1) model.

Key words:traditional GM(1,1);self-adaptive GM(1,1);residual error correction;high-speed railway tunnel; deformation prediction

文章编号:1672-8262(2015)01-142-04中图分类号:P258,TU196

文献标识码:B

收稿日期:∗2014—06—03

作者简介:陈玲菊(1978—),女,工程师,主要从事测绘生产工作。