ArcGIS和分形理论在制图综合评价中的应用
2015-07-04谭忠厚李炜61243部队新疆乌鲁木齐830006
谭忠厚,李炜(61243部队,新疆乌鲁木齐 830006)
ArcGIS和分形理论在制图综合评价中的应用
谭忠厚∗,李炜
(61243部队,新疆乌鲁木齐 830006)
摘 要:以地形图中的居民地和交通路网为研究对象,以分形理论为基础,借助ArcGIS技术,运用居民地的聚集维数模型和交通路网的长度-半径维数模型,分别测算了天山北坡伊-霍经济区1∶25万、1∶50万和1∶100万地形图中居民地和交通路网的加权分形维数,对两大要素的空间分布特征进行定量分析,结果表明:第一,该经济区内居民地和交通路网的空间结构具有明显的分形特征;第二,在中小比例尺地形图中,同一制图区域内随比例尺变化居民地和交通路网的分形维数基本保持不变,分形维数能为制图综合评价、地图质量评价提供一个量化的评价指标。
关键词:分形理论;ArcGIS;聚集维数;交通路网;长度-半径维数;制图综合评价
1 引 言
分形理论[1]最初由美国数学家曼德尔布罗特(B.B.Mandelbrot)于1970年代中期创立,初见于其1967年发表的著名论文《英国海岸线有多长》,文中指出在不同比例尺的地图上度量海岸线会得出迥然不同的结果,应该用分形维数来度量。该理论的一个重要概念是自相似性,即每一个局部放大后与整体一样,整体缩小后与各个局部相同,但这并非数学上的自相似性,因而很难用通常的数学尺度进行度量,描述这种自相似程度的主要参数是分维数。由于分维数的尺度不变性和人们的视觉感知较为一致,分形理论在城镇体系和交通路网分布研究中得到了较为广泛的应用[2~9],其研究范式不断丰富,呈现出多视角、多尺度的研究体系,研究方法也从理论研究发展到理论联系实际、定性研究发展到定性与定量相结合。
运用分形理论对城镇体系和交通路网的研究方法已经很成熟,刘继生、陈彦光等提出并总结出一套城镇体系的等级结构和空间结构的分形维数的测算方法[10~12],石陪基对西北干旱区城镇体系空间结构及其分形进行了研究[13],刘承良对中国四大都市圈的城乡道路网分形进行多尺度比较分析[14,15],刘继生总结了交通路网空间结构分形特征的三种分形维数[16]。由于测绘界只有少数人关注分形理论的发展,其在测绘和数字制图领域中的研究相对较少[17,18],鉴于此,本文以天山北坡伊-霍经济区为例,借助ArcGIS技术通过测算同一制图区域内不同比例尺的地形图的居民地的聚集维数和交通路网的长度-半径维数,研究不同比例尺地形图中居民地和交通要素的分形维数与制图综合评价、地图质量评价的关系,以期为制图综合和图幅质量评价提供一个量化的评价指标。
2 研究区概况
伊-霍经济区位于新疆天山山脉西端,地处亚欧大陆腹地,西与哈萨克斯坦接壤,属中温带半干旱荒漠区,是天山北坡经济带的重要组成部分,主要包括伊宁市、伊宁县、霍城县和察布查尔锡伯自治县。由于地处伊犁河谷地带之中,相对封闭的地形为其城镇体系演化发展提供了相对封闭的地域单元,主要城镇均分布在山间河谷盆地之中,居民地和交通路网的空间分布结构受地形的影响较大。
3 居民地聚集维数的测算
3.1研究模型
聚集维数反映的是制图区域内居民地空间分布的均衡性,较好地揭示了自测算中心向外围居民地的空间分布密度变化。以中心聚落(处于制图区域几何中心位置的最大聚落)或首位聚落(影响力最大,不一定位于区域的几何中心位置)为圆心,以r为半径作圆,统计该范围内居民地的个数N(r),改变半径r,可得到不同的N(r)。
一定区域内,居民地有多种类型,如首都首府、重要城市、一般城市、城镇和村庄等,它们对整个区域的贡献不同,依据重要程度分别赋予不同的权重,设其权重依次为P1,P2…Pn,组成向量P(r)= [P1,P2…Pn]T, 设n种类型的居民地个数分别为L1,L2…Ln,组成向量L(r)= [L1,L2…Ln]T,因此在该区域内,半径为r的范围内加权居民地个数N(r)为:
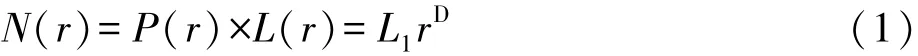
当r由小变大时,N(r)不断增加,在某一范围内(无标度区),N(r)与r满足如下关系:

这是一个分形模型[10,15],即某区域内加权居民地个数与距测算中心的距离r成幂律分布,其中幂指数D即为分形维数,对式(1)两边取对数,将其转化为:

式中,C为待定常数,D为加权聚集维数。
3.2地理意义
聚集维数表示的是以中心聚落或首位聚落为中心,其周边居民地分布密度变化的一种平均情况,反映了区域内居民地分布的均衡性,具有实际应用的价值。正常情况下,0<D<2,D值越大表明区域内居民地的空间分布越均衡,反之则越集中;当D→0时,说明区域内居民地联系紧密,分布高度集中于一地,这种情况现实中一般不存在;当D→2时,表明区域内居民地沿半径方向完全均匀分布,这是一种理想化的状态;当D>2 时,表明随着距测算中心距离加大,居民地呈离散状态分布,显然若测算中心是该区域首位城市,这是一种不正常的居民地空间分布形态,需要进行空间结构优化[19]。
3.3聚集维数的测算及结论
考虑到一般图幅都是矩形,本次研究将聚集维数模型中以r为半径的同心圆换成圆的外接矩形(同心矩阵),本文以制图区域的几何中心伊宁市作为测算中心,分别统计该区域1∶25万、1∶50万和1∶100万地形图中不同半径范围内的加权居民地个数,得到点对序列(r,N(r))。分别以lnr为横坐标,lnN(r)为纵坐标,绘制双对数坐标图(图1),发现存在无标度区,进行线性拟合,得到三种比例尺地形图中基于同一测算中心的居民地加权聚集维数。
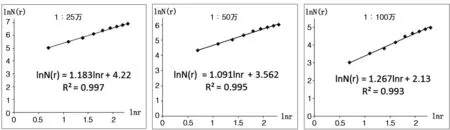
图1 不同比例尺地形图中居民地聚集维数双对数坐标图
结果表明:1∶25万地形图中居民地的聚集维数为1.183,说明该区域内居民地空间分布基本均衡,相关系数R2为0.997,相关性很好,说明居民地空间分布具有明显的分形特征;分维值小于2,说明制图区域内由中心向四周居民地呈逐渐衰减的趋势;分维值比较接近1,通过资料分析发现大部分居民地分布在G218和G312国道沿线一带,具有明显的交通指向性,说明当聚集维数D→1时,可以判断出居民地是沿某一条地理线(如国道、河流)呈带状分布的。
1∶50万和1∶100万地形图中居民地的聚集维数分别为1.091和1.267,相关系数R2均大于0.99, 与1∶25万的分维值相比,变化率分别为7.8%和7.1%,说明1∶50万、1∶100万地形图与1∶25万地形图中居民地空间分布具有相似的分形特征,表明在由1∶25万地形图制作1∶50万或1∶100万地形图中采集居民地要素时,保持了原始数据资料的基本特征,符合综合取舍的基本原则。
4 交通路网长度-半径维数的测算
4.1研究模型
长度-半径维数反映的是区域内交通路网自中心向周边的密度分布的均衡性,假设一定区域内的交通路网由测算中心沿半径向周边以某种自相似规则呈凝聚态分布,则可借助几何测算关系确定半径为r的圆内交通路网总长度L(r)与r的关系,有:

在半径为r的圆内,可能存在n种类型的道路,如铁路、高速、国道、省道、县道、大车路、小路等,它们对整个交通路网的贡献不同,分别赋予不同的权重值,设n种类型道路的权重依次为P1,P2…Pn,组成权重向量:P(r)= [P1,P2…Pn]T,设n种类型道路的长度分别为L1,L2…Ln,组成长度向量:L(r)= [L1,L2…Ln]T,因此,在半径为r的圆内,加权公路总长度LSUM(r)为[15]:
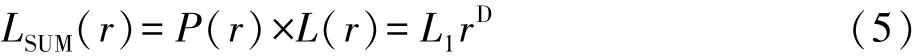
对式(5)两边取对数,将其转化为:

式中,C为待定常数,D为加权长度-半径维数。
4.2 地理意义
正常情况下,长度-半径维数取值范围介于[0~2]之间,D值越高,表明交通路网密度从测算中心向周边地区下降的速率越慢。当D→0时,所有的路网集中于一点,这种情况在现实中一般不会出现;当D→2 时,表明区域内交通从测算中心向周边地带均匀分布,意味着交通路网的发育已经相当完善,但在现实中由于区域间经济发展的不均衡,D值一般不会超过理想值(1.7~1.8);当D→1时,表明大部分道路沿一条地理线分布;若D>2,说明交通路网分布密度自测算中心向周边递增,显然若测算中心是交通枢纽,这种分布是不合理的,理论上需要进行优化[19]。
4.3 长度-半径维数的测算及结论
类似于测算聚集维数的方法,分别统计制图区域1∶25万、1∶50万和1∶100万地形图中不同半径范围内的加权公路总长度,得到点对序列(r,L(r))。分别以lnr为横坐标,lnL(r)为纵坐标,在双对数坐标中获得坐标图(图2),分析图表发现存在无标度区,进行线性拟合,得到三种比例尺地形图中基于同一测算中心的交通路网加权长度-半径维数。
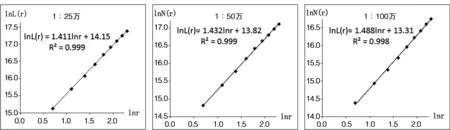
图2 不同比例尺地形图中交通路网长度-半径维数双对数坐标图
结果表明:1∶25万地形图中交通路网的长度-半径维数为1.411,相关系数R2为0.999,说明该制图区域的交通路网具有明显的分形特征;分维值小于2,说明制图区域内由中心向四周交通路网呈现衰减的趋势;若以交通路网长度-半径维数(1.7~1.8)作为判断交通路网空间分布与形态成熟的指标,说明该制图区域内交通路网的空间结构和功能还有较大的发展空间。
1∶50万和1∶100万地形图中交通路网的长度-半径维数分别为1.432和1.488,相关系数R2均大于0.99,同1∶25万的分维值比较,变化率分别为1.5% 和5.5%,说明1∶50万和1∶100万地形图在采集交通要素时,虽然经过制图综合,简化了道路信息,但分形维数基本保持不变,这印证了交通路网分形特征的客观存在性,同时也说明1∶50万、1∶100万地形图与1∶25万地形图的交通路网具有相似的分形特征。表明在由1∶25万地形图制作1∶50万或1∶100万地图中采集交通要素时,较好地保留了原始资料的特征,符合综合取舍的基本原则。
5 结 语
本文运用分形理论,借助ArcGIS技术分析并测算了三种比例尺(1∶25万、1∶50万和1∶100万)地形图中居民地和交通路网的分形维数,初步得到以下结论:第一,伊-霍经济区内居民地和交通路网空间分布均具有明显的分形特征,但由于受山地河谷地形等因素的影响,居民地沿国道呈带状分布,交通路网发育水平较低,空间相互作用较弱,具有较大的发展空间;第二,虽然不同比例尺的地形图经过制图综合,居民地要素和交通路网要素信息量有所简化,但分形维数基本保持不变,表明在由1∶25万地形图制作1∶50万或1∶100万地图中采集居民地和交通要素时,较好地保留了原始数据资料的特征,符合综合取舍的基本原则。说明在中小比例尺地形图中,分形维数以其尺度不变性能为制图综合和地图质量评价提供一个量化的指标。
对未来工作的展望:刻画居民地空间分布形态的分维数还有网格维数、关联维数等,测算交通路网分维值的模型还有计盒维数、节点关联维数等,这些都是地理学分形研究中不可或缺的分形维数的测算模型,在今后的研究中可尝试使用不同分形维数来检查地形图要素采集的合理性。
参考文献
[1] 张济忠.分形[M].北京:清华大学出版社,1995(6):1~15.
[2] 岳文泽,徐建华.甘肃城镇体系结构及其分形模型研究[J].区域研究与开发,2004,23(1):16~23.
[3] 强海洋,张小雷.基于分形理论的新疆干旱区绿洲城镇体系研究[J].干旱区地理,2010,33(5):802~808.
[4] 焦世泰,王世金.基于分形理论的城市区域空间结构优化研究—以兰州-白银城市区域为例[J].西北师范大学学报·自然科学版,2011,47(3):103~109.
[5] 王新涛.基于分形理论的跨省域经济区城镇体系整合发展研究—以中原经济区为例[J].长春理工大学学报, 2012,7(6):50~51.
[6] 朱兵,张小雷.西部欠发达地区城镇体系分形研究—以兰州-西宁城镇密集区为例[J].干旱区研究,2011,27 (3):458~466.
[7] 苏海宽,刘兆德.基于分形理论的鲁南经济带城镇体系分布研究[J].国土与自然资源研究,2011(2):76~78.
[8] 陈杰,马素媛.顾及尺度全国主要省市道路网分形维数的研究[J].测绘与空间地理信息,2012,35(8):145~147.
[9] 陈斌峰,吴志峰.基于分形理论与GIS的城区交通路网复杂性分析—以广州市城区为例[J].热带地理,2011, 31(1):46~51.
[10] 刘继生,陈彦光.城镇体系等级结构的分形维数及其测算方法[J].地理研究,1998,17(1):82~89.
[11] 刘继生,陈彦光.河南省城镇体系空间结构的分形特征及其与水系分布的关系探讨[J].地理科学,2003,23 (6):713~720.
[12] 刘继生,陈彦光.城市地理学的分型研究的回顾与前瞻[J].地理科学,2000,23(2):166~171.
[13] 石陪基,刘海龙.西北干旱区城镇体系空间结构及其分形—以酒泉为例讨[J].经济地理,2007,27(6):918~921.
[14] 刘承良,段德忠.中国四大都市圈城乡路网分形的多尺度比较分析[J].经济地理,2013,33(3):52~58.
[15] 刘承良,段德忠.武汉城市圈城乡路网空间生长的分形研究[J].交通运输系统工程与信息,2013,13(5):185 ~193.
[16] 刘继生,陈彦光.交通网络空间结构的分形维数及其测算方法探讨[J].地理学报,1999,54(5):471~478.
[17] 廖祥春.分形理论及其在测绘和其他领域中的应用[J].测绘科技通讯,1994,17(4):26~30.
[18] 向飞,杨海峰.分形在快速测绘保障中的应用[J].解放军测绘学院学报,1996,13(3):224~227.
[19] 林涛,孙婷婷.长江三角地区高速公路网络与城镇体系空间结构的分形研究[J].人文地理,2012,128(6):43 ~49.
The Application of ArcGIS and Fractal Theory in Cartography Generalization Evaluation
Tan Zhonghou,Li Wei
(PLA 61243 Troops,Urumqi 830006,China)
Abstract:Taking resident and traffic network(RTN) of topographic map as an example,based on the Fractal Theory and ArcGIS technology,this paper establishes two fractal model including aggregationdimension of resident and length-radius dimension of traffic network,so as to measure the weighted fractal dimension of Yining and Huocheng economic areas in 1∶250 000、1∶500 000 and 1∶1 000 000 scale respectively and explore the spatial distribution characteristics of RTN by means of quantitative analysis.The results show that:firstly,the RTN spatial structure has fractal characteristicsin drawing region,which are in line with the qualitative analysis;Secondly,in the same drawing region,when changing the map scale,it does little effect on fractal dimension in middle and small scale topographic map;Finally,it puts forward a conclusion:the fractal dimensioncan provide a quantitative index for cartography generalizationevaluation and map quality evaluation.
Key words:the fractal theory;ArcGIS;aggregation dimension;transport network;length-radius dimension;cartography generalization evaluation
文章编号:1672-8262(2015)01-56-04中图分类号:P208,F209
文献标识码:B
收稿日期:∗2014—07—03
作者简介:谭忠厚(1985—),男,硕士,主要从事遥感与地理信息系统。
