大区域非解析空间数据坐标无缝转换技术研究
2015-07-04张涛劳洁英常永青王庆南京市规划局江苏南京009滁州学院地理信息与旅游学院安徽滁州9000南京市测绘勘察研究院有限公司江苏南京009
张涛,劳洁英,常永青,王庆(.南京市规划局,江苏南京 009; .滁州学院地理信息与旅游学院,安徽滁州 9000; .南京市测绘勘察研究院有限公司,江苏南京 009)
大区域非解析空间数据坐标无缝转换技术研究
张涛1∗,劳洁英2,常永青1,王庆3
(1.南京市规划局,江苏南京 210029; 2.滁州学院地理信息与旅游学院,安徽滁州 239000; 3.南京市测绘勘察研究院有限公司,江苏南京 210019)
摘 要:剖析现有大区域非解析空间数据坐标转换方法主要缺陷的基础上,研究建立了以地理经纬网线为基本约束,以大地线长度为权重因子的分区无缝空间数据坐标转换模型。实验测试表明,基于不同大小的经纬网格约束,该模型不仅能满足不同尺度空间数据坐标转换精度,而且避免了在不同转换区域边界处的空间数据二次接边,具有较好的实用性。
关键词:坐标转换;经纬网约束;空间数据;大区域
1 引 言
在以信息技术为代表的当代新技术革命中,人们用前所未有的能力去获取关于地球和人类社会的巨量信息,例如数字地球、数字国家、数字城市等建设。在这个过程中,大区域的自然资源与地理空间数据库的建设与管理,已成为各个地方空间基础设施建设的主要任务。因此,实际应用中会经常面临大量的空间坐标转换工作,且他们之间没有严密的数学解析关系,这使得空间数据的坐标转换已成为多源空间数据集成和测绘生产等过程中经常发生的基本操作。
目前,建立解析变换和非解析变换[1~10]方法获得国内外众多学者的关注,研究重点是非解析变换模型。现有的坐标转换方法仍然存在两个比较突出的问题:一是当前的研究大多数集中在小区域坐标转换,在大区域坐标转换的过程中,传统的投影分带方法将大区域投影到平面上产生的变形太大,转换精度不能有效保证。二是利用图幅网格约束的球面坐标转换能够解决投影变形问题,但是会带来相邻图幅二次接边过程。如将整个大区域数据当成一个图幅来处理,整个图幅变换后不会出现边界不一致需要拼接的问题,但是很显然图幅内部转换精度达不到要求;如果将大区域内的每个图幅单独进行坐标变换,各个图幅的转换精度能够达到要求,但是每个图幅的图廓边界将面临不重合,图幅间需要重新拼接。
针对传统的方法不能完成大区域非解析空间坐标的无缝转换问题,本文借鉴逐格网转换思想,构建以球面为基准,以图幅网格为约束,以球面距离为加权因子的大区域非解析空间坐标快速转换新方法,以期实现大区域空间坐标全覆盖、无重叠、无缝隙、高精度、高效率的转换。
2 图幅格网约束坐标转换原理
逐图幅格网约束的空间坐标转换的基本思想是,首先是在整个大区域内,依据不同比例尺要求,按照一定的图幅间隔,将整个大区域数据划分为小的图幅格网单元,然后对空间数据进行逐经图幅网纠正。对具体的任意数据点来说,以该点所在图幅格网的格网点作为控制点,采用球面距离加权的方法进行加权求和转换。所谓球面距离加权是以数据点和图幅网交点构成的区域的两条边线长度为加权因子,分别将对应格网点的权重和改正量相乘再求和,则为数据点的改正量。具体实现如图1所示:

图1 基于经纬网约束的空间数据坐标变换示意图
对于图幅格网内任意一个点P(B,L)或P(X,Y),其改正量(△B,△L)或(△X,△Y)应该与四个格网点改正量以及权重相关。每个格网点对应的权重为P点的坐标与格网点构成的区域边线长度相乘。假设D1、D2、D3、D4为其边线长。
改正量(△B,△L)有如下计算公式:
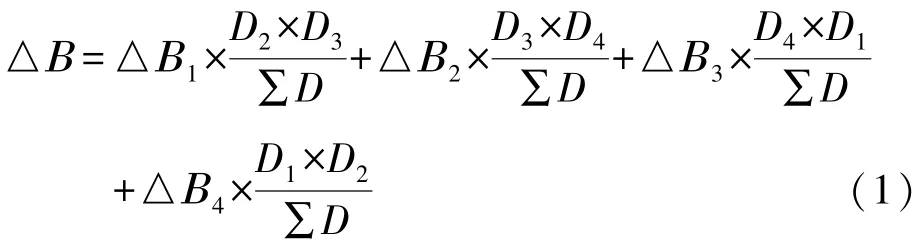
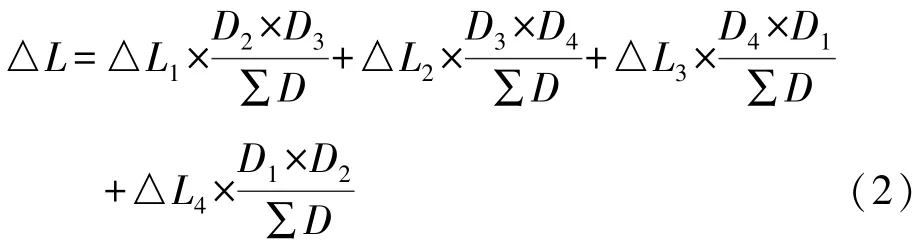
其中:∑D=D1×D2+D2×D3+D3×D4+D4×D1。
当点P位于经纬(图幅)格网点P2上时,D1= 0, D2= 0,△B=△B2,△L=△L2。所以,点P位于格网点Pi时,改正量只与该点有关;
当点P位于经纬(图幅)格网线P2P3上时,则D2= 0,因此:
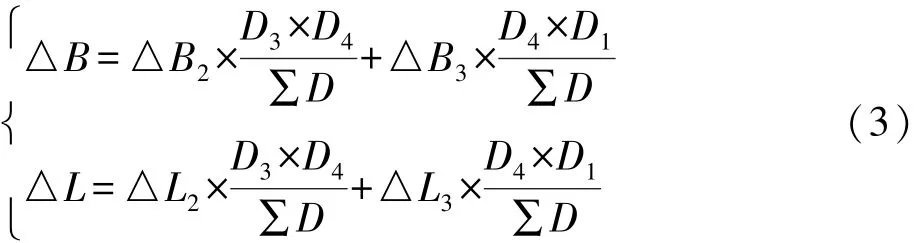
那么改正量(△B,△L)就受该线上两个格网点P2,P3所控制,其权重比值可简化为D3:D1。因此,对于相邻经纬(图幅)格网来说,其格网的变换不受其他要素所影响,变换之后能够保证格网完全重合。
3 逐图幅格网转换实现过程
(1)图幅网的布设。在不同的比例尺下,按照图幅(一定的经差和纬差)完成图幅网的布设,每个格网点记录当前坐标值和待转换目标坐标值。这样,格网点的变换改正值就为待转换目标坐标值与当前坐标值之差。
(2)坐标变换计算。读取待转换数据坐标点P (B,L),先按照格网索引快速定位到所在格网,然后计算P点到图廓边线的距离D1、D2、D3、D4和图廓点的权重W1、W2、W3、W4,最后利用第二部分的公式计算得到坐标变换值。其中涉及的计算有:
①格网行列号的计算:如图2所示,设经纬网左下角的坐标为P0(B0,L0),P点坐标为(B,L),则P点的行列号(i,j)计算公式为:
i=(int)(L-L0) /2,j=(int)(B-B0) /3(6)
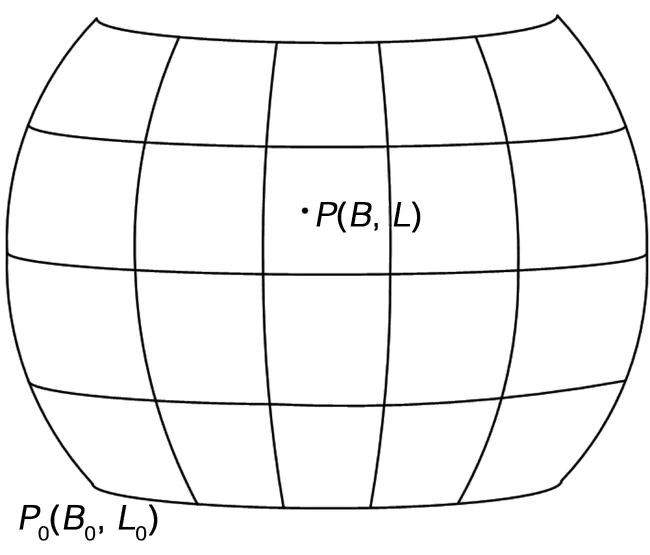
图2 行列号计算
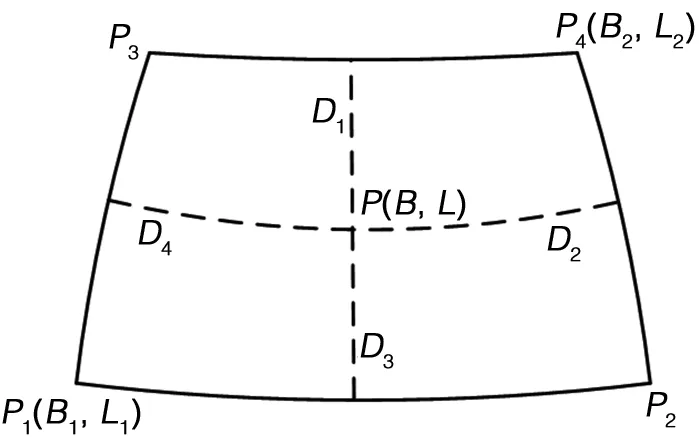
图3 球面距离计算
②球面距离的计算:如图3所示根据P点的行列号可计算出P1(B1,L1)和P2(B2,L2)的坐标,B1=B0+ (j∗3),L1=L0+(i∗2),B2=B1+3,L2=L1+2。则P到经纬格网四边的距离D1、D2、D3、D4分别为:π
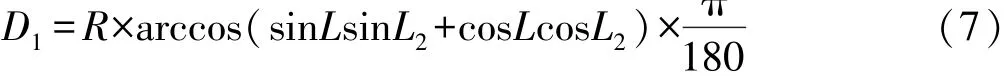


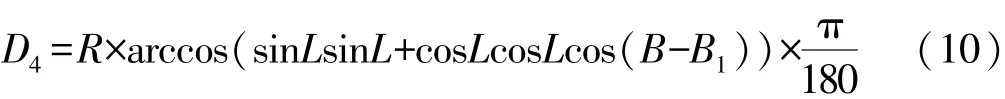
③格网点权重的计算:P1的权重为W1= D1×D2/ ∑D,P2的权重为W2=D1×D4/∑D,P3的权重为W3= D2×D3/∑D,P4的权重为W4=D3×D4/∑D,其中

④代入坐标转换的公式计算P点的改正值(△B, △L)。
(3)应用实践
该方法用在南京市市域92南京地方系向2008南京地方坐标系成果转换的项目中,成果经过外业检测,成果质量满足技术设计要求,并通过南京市规划局组织的专家验收,达到了项目预定的目标。
4 结论与展望
(1)研究表明,该模型在精度、效率及转换结果等方面,均能较好满足不具有严密数学解析关系的大区域空间数据坐标得要求。尤其当前我国在不断完善和发展空间坐标系统,对实现高精度、高效率的空间坐标转换具有良好的应用性。
(2)由于一些坐标系下的控制点坐标信息具有保密性,这使得许多基层单位不能规范完成。该模型不需要提供高度保密的控制点坐标信息,避免了保密和公共服务的矛盾。
(3)本文中构建的模型是基于标准地形图进行分幅,其每个图幅是面积不等的规则图形。如果进行面积相等或图形不规则区域的空间坐标转换该模型是否适用,值得深入研究。
参考文献
[1] 郭充,吕志平,于兴超等.基于Bursa加权模型的格网坐标转换[J].测绘科学技术学报,2009(2).
[2] 王解先,王军,陆彩萍.WGS-84与北京54坐标的转换问题[J].大地测量与地球动力学,2003(3).
[3] COLLIER P A,LEAHYFJ,ARGESEANU V S.Transition to the Geodetic Datum 2000[J].Times of Geographical Survey Institute,2001,97:31~57.
[4] 于彩霞,黄文骞,攀沛.Bursa的3参数模型与7参数模型的适应性研究[J].测绘科学,2008(2).
[5] 丁士俊,张忠明.几种不同坐标变换方法问题的研究[J].四川测绘,2005(1).
[6] 李宏.空间直角坐标至大地坐标的直接严密变换[J].测绘与空间地理信息,2007(6).
[7] Krarup T.A contribution to the mathematical foundation of physical geodesy[R].Copenhagen: Danish Geodetic Institute,1969.
[8] 吕志平,乔书波.大地测量学基础[M].北京,解放军出版社,2005.
[9] 乔连军,韩雪培.1954北京坐标与1980西安坐标转换方法研究[J].测绘与空间地理信息,2006(1).
[10] 王建弟,张伟.用二次多项式实现54坐标到80坐标的转换[J].矿山测量,2005,9(3).
Research on Seamless Conversion Technology of Large Area Non Analytic Spatial Data
Zhang Tao1,Lao Jieying2,ChangYongqing1,Wang Qing3
(1.Nanjing Planning Bureau,Nanjing 210029,China; 2.College of Chuzhou Geographic Information and Tourism College,Chuzhou 239000,China; 3.Nanjing Institute of Surveying,Mapping &Geotechnical Investigation,Co.,Ltd.,Nanjing 210019,China)
Abstract:Based on the analysis of the main defects of the existing large area non analytical spatial data coordinate transformation method,the paper studies the spatial data conversion model based on the geographic latitude and longitude as the weight factor.Experiments show that the model can not only satisfy the conversion accuracy of different scale spatial data,but also avoid the spatial data of two times,which has good practicability.
Key words:coordinate transformation;the network constraint;spatial data;large area
文章编号:1672-8262(2015)06-66-03中图分类号:P226+.3
文献标识码:B
收稿日期:∗2015—09—07
作者简介:张涛(1963—),男,高级工程师,主要从事测绘管理、沉降监测方面的研究。
基金项目:国家自然科学基金(41174002 )
