数值模拟盾构不同角度穿越砌体结构房屋

吴海峰,魏纲(1．杭州市勘测设计研究院,浙江杭州 31001; ．浙江大学城市学院土木工程系,浙江杭州 310015)

数值模拟盾构不同角度穿越砌体结构房屋

吴海峰1∗,魏纲2
(1．杭州市勘测设计研究院,浙江杭州 310012; 2．浙江大学城市学院土木工程系,浙江杭州 310015)

摘 要:盾构法隧道施工会对周围土体产生扰动,进而引起地面沉降,导致邻近建筑物倾斜、开裂乃至坍塌等一系列问题。对于如杭州这样的建筑方位不规整城市,在地铁施工中经常会遇到隧道以一定角度从建筑物下方或邻近穿越的工况,将引起建筑物的永久性扭曲变形[1],产生较大危害。本文采用三维MIDAS/ GTS软件,模拟盾构隧道以0°、22．5°、45°、67．5°、90°穿越引起的建筑物附加沉降及墙体受力,分析盾构不同角度穿越砌体结构房屋规律。

关键词:盾构;砌体结构;沉降

1 前 言

目前关于盾构法隧道施工对建筑物影响的研究方法主要有:解析方法[1～2]、和有限元方法[3～7]等。其中有限元方法应用最多,研究发现:①对框架结构建筑物的研究较多[3～6]。对砖混结构建筑物的研究较少[7],虽然采用了三维模拟,但都比较简单,存在不足:如没有详细研究随盾构机开挖面穿越前后,建筑物的受力与变形规律;盾构施工模拟中没有考虑正面附加推力、盾壳摩擦力和注浆影响,不够精细;没有考虑土质条件、建筑物层数、隧道与建筑物水平及垂直位置改变等影响因素;②绝大多数都是研究隧道平行或垂直穿越建筑物的工况[3～7],仅文献[7]对隧道斜穿建筑物工况进行研究,但该文在研究中将建筑物简化为等效荷载,存在不足。综上所述,目前对盾构隧道不同角度穿越砖混结构建筑物工况的研究还不多,需要深入研究盾构以什么角度穿越建筑物比较合理。

2 邻近建筑物工况的盾构隧道施工三维有限元模拟

2．1模型建立及参数取值

盾构隧道外直径为6．3 m,隧道轴线埋深为12 m,盾构机身长8 m,盾壳厚7 cm。衬砌每环宽1 m,厚0．35 m,采用C50混凝土。建筑物墙体为砖混结构,地上2层,每层高3 m,横向为3开间,纵向为2开间,墙轴线间距均为4．3 m,墙体厚0．3 m,外轮廓为13．2 m×8．9 m。墙上开门及窗,门的大小为2 m×1 m,窗为1．5 m×1 m,窗下沿距地面1 m,门与窗均位于两堵墙的中间位置。为建模方便和尽量减少单元数,在有限元模拟中采用荷载代替楼板的自重与活载,在墙顶面上施加均布荷载30 kPa。基础为条形基础,采用C20混凝土,埋深1．5 m,宽0．6 m,外轮廓为13．5 m×9．2 m。整个模型在横向取80 m,竖向取40 m,纵向取70 m。

假定土体为均质土层,本构模型采用莫尔-库伦模型。衬砌、墙体和基础均采用线弹性模型。盾壳和衬砌采用板单元,墙体、基础和土体均采用实体单元。通过对墙体材料弹性模量进行折减,来考虑砖混墙体为非连续介质及其随时间的损耗和房屋破损。模型计算参数如表1所示。

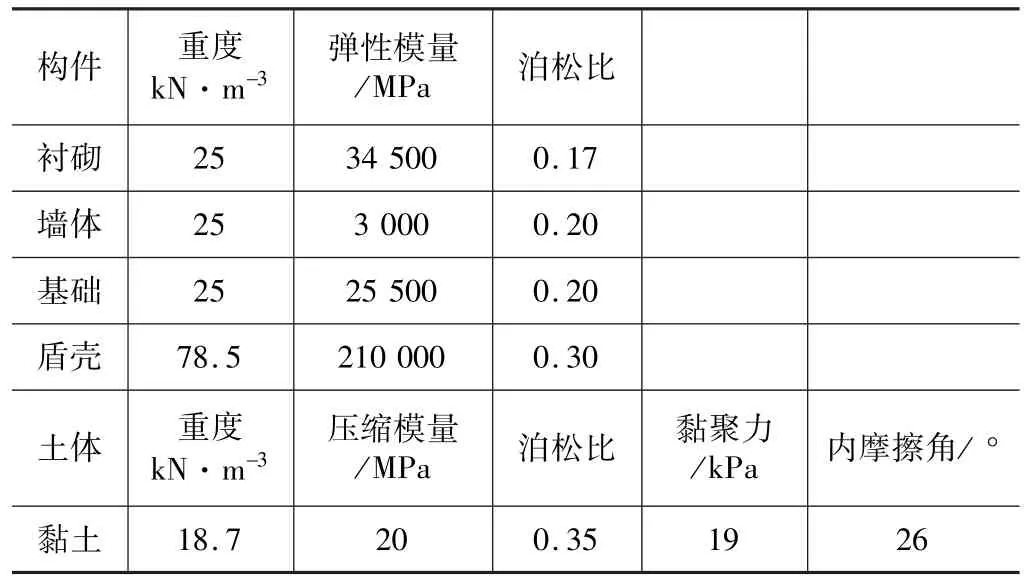
材料物理力学参数 表1

如图1所示,为便于比较,模拟时盾构隧道轴线均通过建筑物中心点即两条轴线交叉处),令隧道开挖面与建筑物横墙的夹角为α,分别取α= 0°、α= 22．5°、α=45°、α=67．5°、α=90°。令纵墙命名为A、B、C、D,横墙命名为Ⅰ、Ⅱ、Ⅲ。隧道掘进方向采用y坐标表示,令开挖面到达建筑物中心点时掘进距离y=0,掘进距离y到达前定义为负值,通过后定义为正值。网格划分如图2所示。

图1　建筑物与隧道俯视图(单位/ m)

图2　网格划分图

2．2有限元模拟步骤

模拟时假定:①忽略地下水的渗透作用,土体本身变形与时间无关;②墙体与基础,基础与土体采用变形协调计算的方法;③隧道开挖前地面沉降为零,即不考虑建造建筑物引起的地面沉降。

有限元模拟步骤包括:①模拟土体生成,考虑土体自重,位移清零,只保留应力;②模拟建筑物生成,考虑建筑物自重和顶部荷载,位移清零,只保留应力;③采用“刚度迁移法”模拟盾构推进过程,盾构机每向前推进一步作相应变化:杀死该开挖步处的土体单元,土体释放应力,在开挖面处施加支护力,激活盾壳单元,施加摩擦力;将最后面一段原盾壳单元修改单元属性,变为衬砌单元,去掉摩擦力,施加注浆压力。实际工程中每环衬砌宽1 m,为减少计算量,每个开挖步杀死2 m的土体单元。盾壳与土体之间的摩擦力和开挖面支护力均假定为均布力,摩擦力和正面附加推力分别取45 kPa和20 kPa[8]。采用等效均布力来模拟盾尾同步注浆,取值为37 kPa[3]。

3 有限元计算结果分析

3．1位移分析

经过计算,如果不考虑建筑物,盾构施工引起的地面沉降曲线呈正态分布,与Peck公式预测值很吻合,最大地面沉降量为11．41 mm,地面沉降槽宽度系数i=kh =0．48×12=5．76 m,土体损失率为0．53%,表明有限元模拟的可靠性。限于篇幅,本文仅研究部分数据。

图3中的中心点为建筑物的几何中心(见图1)。如图所示:①在开挖面通过前,基础先产生微小的隆起,随后产生急剧沉降;当开挖面刚通过基础(y=12 m)时,沉降达到最大值;当开挖面远离建筑物后,沉降值趋于稳定;②当y<8 m之前,不同角度穿越引起的中心点竖向变形曲线数值很接近,几乎一致; (3)当y＞8 m后开始分散,并随角度的增大而增大, 67．5°与90°之间仍保持一致并且数值很接近。

图3　中心点不同角度基底沉降比较

图4为y=44 m盾构不同角度穿越时横墙I基础顶面沉降曲线,此时建筑物沉降已稳定。由图可知:①当隧道轴线与墙体垂直时墙体的沉降曲线呈现中间大两边小;②22．5°、45°、67．5°穿越时变化规律基本相同,呈现单调减小。并且22．5°的沉降量<45°的沉降量<67．5°的沉降量;③当隧道轴线与墙体平行时沉降曲线基本成一条水平直线。

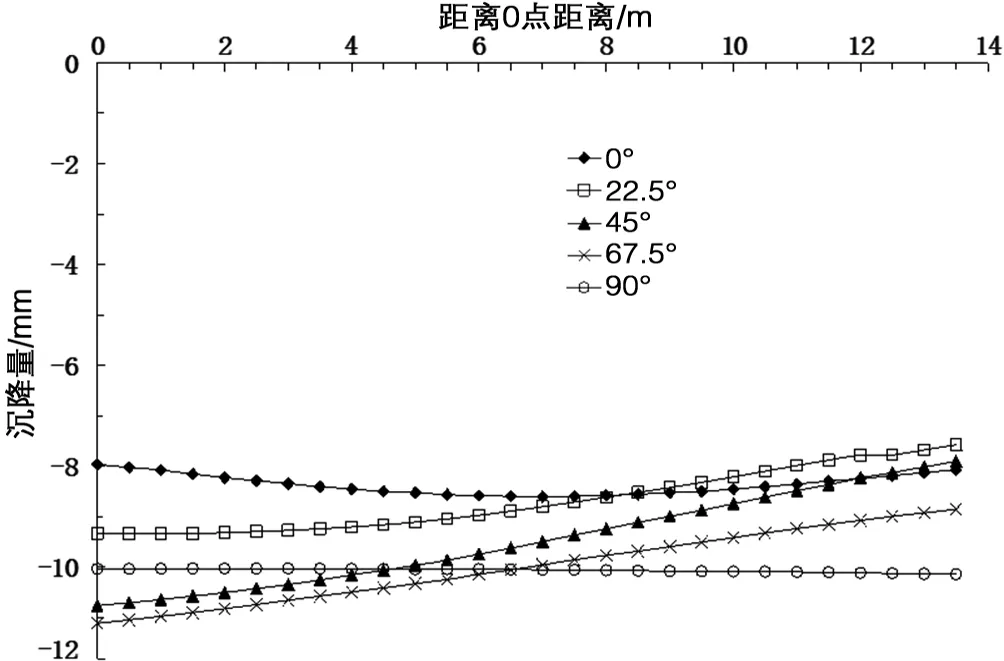
图4　不同角度时横墙I基础顶面沉降比较(y=44 m)

图5为不同角度穿越时横墙I的首尾沉降差比较。如图所示:①沉降差除0°穿越外均呈现先增大后减小的特点;当开挖面到达建筑物中心点(y=0)时,沉降差均达到峰值;0°时隧道与横墙I垂直,此时横墙Ⅰ的沉降曲线呈对称分布(如图5所示),故首尾沉降差几乎为零;②在各角度穿越过程中,67．5°穿越时在开挖面到达建筑物中心点时沉降差最大(此时墙体与隧道轴线成22．5°时),表明此时墙体比较危险;③90°穿越时的首尾沉降差变化最大,0°穿越的首尾沉降差变化最小。

图5　不同角度穿越时横墙I首尾沉降差比较

图6为盾构掘进过程中最大纵向水平位移变化比较,纵向水平位移以图1中y方向为正。由图可知:①不同角度穿越引起的变化曲线比较相似;②当开挖面到达建筑物中心轴时,各角度穿越时的最大纵向水平位移均达到最大值,45°穿越时值最大。

图6　盾构掘进过程最大纵向水平位移变化比较

图7为α= 45°,y =44 m时放大后的建筑物竖向变形示意图(向图内为掘进方向),当隧道斜穿建筑物工况时,由于隧道施工引起的地面横向沉降槽呈正态分布,导致靠近隧道轴线侧的建筑物沉降要比远离隧道轴线侧的大,使建筑物产生永久的双向不均匀沉降,此时建筑物受扭。

图7　放大后的建筑物变形(α=45°,y=44 m)

3．2应力分析

砖混结构的裂缝或破坏一般由剪应变或拉应变超过其允许值引起[9]。最开始的裂缝是由剪切变形导致的,如图8所示:①随着盾构掘进距离增大,墙体最大剪应变先略微减小,原因是由于基础产生微小隆起;随后逐渐增大,最后趋于稳定;②各角度穿越均在y=4 m ～12 m之间时达到剪应变最大(墙体开裂程度最大),而最大差异沉降位置发生在y=0 m时,所以说明墙体差异沉降大小与最大剪应变不存在直接关系,不能单以差异沉降量来判断砖混结构建筑物的安全性。当y ＞22 m后,剪应变基本趋于稳定且大于初始值,原因在于建筑物产生永久的扭曲变形;③从剪应变曲线可以看出,随着角度增加隧道开挖对建筑物产生的永久扭曲变形减小,0°产生的墙体最大剪应变最大,其次是22．5°、45°、67．5°、90°,67．5°与90°比较接近。

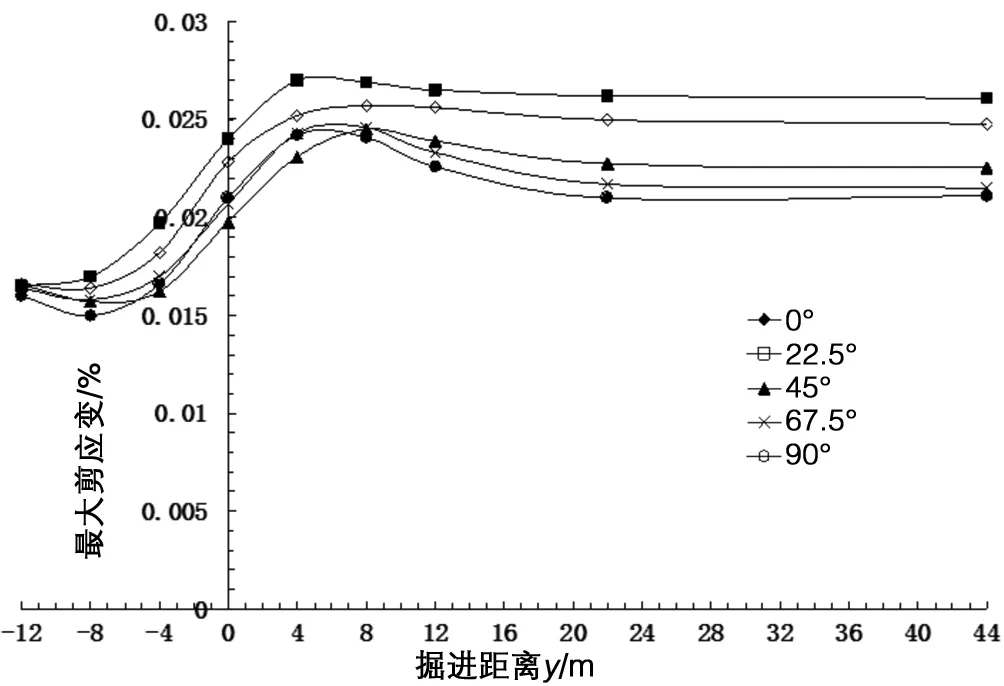
图8　最大剪应变曲线比较

4 结 论

(1)建筑物基底沉降量变化趋势基本相同,均是迅速增大达到最大值(y=12 m)后有所回弹,然后趋于稳定。中心点则呈现随角度增加而增大的现象。

(2)建筑物沉降稳定时,隧道轴线与墙体垂直时墙体的沉降曲线呈现中间大两边小,22．5°、45°、67．5°穿越时变化规律基本相同,呈现单调减小,并且22．5°的沉降量<45°的沉降量<67．5°的沉降量。当隧道轴线与墙体平行时沉降曲线基本成一条水平直线。

(3)随着盾构掘进距离增大,墙体最大剪应变先略微减小,随后逐渐增大,最后趋于稳定且大于初始值。随着角度增加,隧道开挖对建筑物产生的永久扭曲变形减小,0°产生的墙体最大剪应变最大,其次是22．5°、45°、67．5°、90°,67．5°与90°比较接近。

参考文献

[1] 韩煊,Jamie R Standing,李宁．地铁施工引起的建筑物扭曲变形分析[J]．土木工程学报,2010,43(1):82～88．

[2] CHUNGSIK Y,JAE-HOON K．A web-based tunneling- induced building/ utility damage assessment system: TURISK [J]．Tunnelling and Underground Space Technology,2003, 18(5):497～511．

[3] 丁智．盾构隧道施工与邻近建筑物相互影响研究[D]．杭州:浙江大学,2007．

[4] 彭畅,伋雨林,骆汉宾等．双线盾构施工对邻近建筑物影响的数值分析[J]．岩石力学与工程学报,2008,27(S2): 3868～3874．

[5] 李浩,王涛,徐日庆．隧道施工对框架结构及地表位移影响的数值分析[J]．铁道工程学报,2008,(9):58～61．

[6] MROUEH H,SHAHROUR I．A full 3-D finite element analysis of tunneling - adjacent structures interaction [ J]．Computers and Geotechnics,2003,30:245～253．

[7] 苏卜坤,石玉华,张洪彬．地铁盾构施工对上部房屋的影响及加固效果分析[J]．珠江现代建设,2009(6):30～33．

[8] 魏纲,张世民,齐静静等．盾构隧道施工引起的地面变形计算方法研究[J]．岩石力学与工程学报,2006,25(S1): 3317～3323．

[9] Boscardin M D,Cording E J．Building response to excavation -induced settlement[J]．Journal of Geotechnical Engineering,1989,115(1):1～21．

Numerical Simulation of Shield Through the Masonry Structure at Different Angles

Wu Haifeng1,Wei Gang2
(1．Hangzhou Geotechnical Engineering and Surveying Research Institute,Hangzhou 310012,China; 2．Department of Civil Engineering,Zhejiang University City College,Hangzhou 310015,China)

Abstract:Shield Construction will result in disturbances to the surrounding soil,thus causing ground settlement, leading to adjacent structures a series of problems such as tilt,crack and even collapse．Subway tunnel construction always crosses through with a certain angle at the bottom of adjacent building inHangzhou,which will cause permanent distortion to buildings．By using three-dimensional MIDAS/ GTS software,shield crossed the building with 0 degree,22．5 degrees,45 degrees,67．5 degrees,90 degrees was simulated,and the additional settlement of building and wall stress were also analyzed．Analysis of different angles crossing the masonry structure building．

Key words:shield;building;settlement

文章编号:1672-8262(2015)06-158-04中图分类号:TU91

文献标识码:A

收稿日期:∗2015—05—13

作者简介:吴海峰(1988—),男,助理工程师,主要从事岩土工程设计等技术工作。