光学扫描法测金属杆直径

2015-07-03李美莹李金环

大学物理实验 2015年4期

李美莹，刘凯，李金环

(东北师范大学，吉林长春 130024)

光学无损检测已经在食品、农业、医疗等行业得到了广泛的应用［1］，在测量行业也具有长足的发展，根据D=Kλ/S可以方便的计算出细丝直径［2］，并有办法在理论上将相对测量误差控制在0．4%［3］。但是这种办法测量的范围很有限，大概在0．05 mm～0．5 mm。本文介绍一种方法，测量范围在0．5 cm～2 cm级别依然适用。当平行光照射到金属杆上时，经过金属杆边缘的光会发生菲涅尔直边衍射，利用光电池与检流计构成的系统可以测定光强与位置坐标之间的关系。根据理论推导可知，光强为最大光强1/4的位置为几何阴影边缘，进而可以确定金属杆的直径。

1 菲涅尔直边衍射理论

根据菲涅尔-基尔霍夫衍射公式［4］:

其中A是常数，r是光源指向衍射孔的向量，s是衍射孔指向光源的向量，n是衍射波传播的方向向量。如果P0和P两点距离屏的距离比孔的尺寸大很多，则因［cos(n，r)－cos(n，r)］在整个孔上变化不明显，可用2cosδ来代替，δ是直线和P0O与0P屏法线的夹角。设(ζ，η)为孔上某点Q的坐标，则方程可化为:

在菲涅尔直边衍射的情况下可写成:

强度函数:

由矢量图解法(利用考纽螺线)从理论上得到的光强分布如图所示［5］。从图中可以看出，无论在几何阴影内部还是外部，光强均没有发生突变。

图1 直边衍射光强分布曲线

2 实验测量

2．1 实验装置

实验室用氦氖激光器出射的光束能量集中，直径比较小，为了使被测金属杆两侧能同时形成直边衍射现象，需要将光束扩展为照射范围较大的平行光源。实验中使用一组凸透镜的望远系统可以简便地完成光源的扩束。当平行光入射，在金属杆边缘形成菲涅尔直边衍射，用光电池检测每一位置对应的光强，画出光强-位置曲线。实验中采用的光源为JD-I型氦氖激光电源，测量光强的装置为硅光电池串联AC15直流复射式检流计，分度值为2．2×A/div。实验装置如下图所示。将激光器，透镜组，金属杆，硅光电池依次摆放在光具座上，将硅光电池安放在可垂直光具座方向移动的支架上，并连接AC15直流复射式检流计。硅光电池由底座固定在光具座一端，通过旋钮可以移动它的位置，并且可以读出位置的坐标。

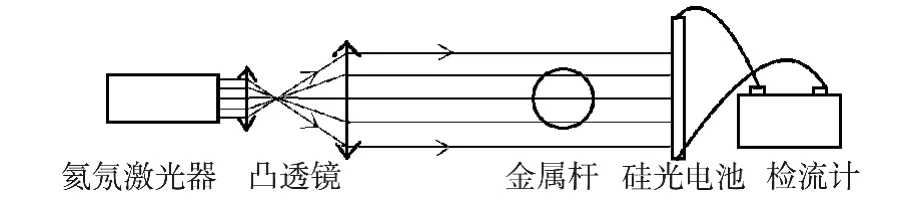
图2 装置图

2．2 平行光的获得

实验用氦氖激光器发射光束直径约为2 mm，可以通过两只焦距为10 cm的凸透镜组成扩束镜来完成扩束。将透镜组移动至距光源10 cm左右处，调节两凸透镜之间的距离，取光屏置于透镜组与金属杆之间，当光屏位置前后移动而光斑大小不变时，则认为出射光为平行光，将此时两透镜的位置固定。

为了方便与金属杆的衍射图样进行对比，首先测试了没有金属杆遮挡情况下的光强分布曲线。实验需在黑暗环境下进行。先将光标调到刻度盘最左侧，取×1档位即可。移动水平螺钮，使硅光电池狭缝暴露在光强稳定区，此时检流计光标会向右偏转，快速将光电池从扩展光束处移过，观察检流计光标，若光强最大处光标超过最右侧刻度，说明光电池狭缝过大，调小狭缝重新测量。适当调节狭缝宽度使光标偏转始终在最大量程的90%以内，确保在激光器功率不稳定的情况下不超量程。每0．1 mm移动一次硅光电池的位置，同时读取光的强度，单位为div。测量结果如图3所示。

图3 无被测物体时平行光的光强分布

从图中可以看出，由于透镜组口径的限制，光束大概能被扩展成直径25 mm的平行光。由于激光器发射不稳定性、硅光电池的灵敏性、透镜曲率精度及所用元件的表面清洁程度等影响，在平行光区，光强的分布不够均匀。但是通过该光强分布曲线，大概判断被测金属杆在光路中应该放置的位置，确保被测金属杆两侧的光强在衍射发生前尽可能一致。待测金属杆直径为1．00 cm，因此选择将其放在左侧2 mm处，金属杆两侧的光强大约都是78div。

2．3 直径测量

将待测金属杆放到检流计前，并移动到中心位置在左侧2 mm的位置。当平行光入射时，金属杆的两侧边缘都会发生菲涅尔直边衍射，衍射条纹会对称分布在几何阴影两侧。

调好初始状态后将光电池移动到一端，开始进行数据的测量。在衍射区外，可以每移动0．1 mm测一个数据，在靠近金属杆边缘的衍射区内每移动0．05mm测量一个数据，保证测量数据的准确性及曲线的平滑度。然后利用计算机进行数据处理，绘制成I(光强)-X(位置)曲线，所得结果如图4所示。

图4 放入被测金属杆后的衍射图样光强分布

图4 可以看出，左侧衍射区的光强应为80div，几何边缘处的光强应为20div，因此得到金属杆左侧几何阴影位置坐标为－6．70 mm，同样算出右侧几何阴影边缘位置为3．72 mm，则本次测量金属杆的直径为10．42 mm．使用螺旋测微器再次对金属杆进行测量，3次测量的平均值为10．462 mm。

由于激光器发射功率不稳定、外界光源对光电池造成干扰、平行光不严格平行等原因，该测量方法也会产生一定的误差。多次测量求平均值可以减小随机误差。按照上述方法对同一根金属棒进行6次测量，结果如表1所示。

表1 扫描法多次测量金属杆直径结果

多次测量的平均值

用螺旋测微器进行验证性测量，多次测量的平均值为10．442，以此数值为对照，用光学扫描法测得金属杆直径的相对误差为

2．4 误差分析

该实验测量存在偶然误差和系统误差。系统误差主要体现在激光器发射功率不稳定，检流计偏转不敏感及凸透镜的球差与像差等三个方面，在实际操作中无法避免，可以通过使用更高性能的实验器材来缩小。偶然误差主要体现在检流计读数误差及平行光的调节不准确等两个方面。下面对平行光调节不准对实验结果的影响情况进行讨论。

图5 微发散光束下直径测量光路图

在实验中，我们是通过人眼识别近处(距扩束镜2 cm)光斑和远处(距扩束镜2 m)光斑直径大小一致判定平行光的。在测量光斑大小的过程中使用了精度为1 mm的刻度尺。由于扩束镜边缘会发生衍射现象，且外界环境黑暗，光斑直径的测量有一定误差．我们认为，当近处光斑与远处光斑直径大小相差小于1 mm时，即判定为平行光调节完毕．这样一来，平行光模型即为微发散光或微会聚光的近似．以发散为例，如图5所示光路:

近处光斑直径为d=25 mm，远处光斑直径D=26 mm，透镜组与远处光斑距离l=2000 mm，则的距离为3 cm，则由发散角引起的误差约为Δx=0．25 mrad ×0．03 m=0．007 5 mm。

微汇聚光束下的情况相似，对直径测量的误差影响也在0．001 mm数量级上。我们发现，为了得到更精确的测量结果，缩短金属杆与硅光电池的距离是最有效最简便的方法。