三势阱玻色爱因斯坦凝聚体三体复合效应的数值研究
2015-07-03穆爱霞朱天荣
穆爱霞,朱天荣
(平凉医学高等专科学校,甘肃平凉 744000)
玻色-爱因斯坦凝聚(Bose Einstein condensates,简称BEC)是一全新的超低温量子物态,是物质的一种奇特的状态,是一种宏观的量子简并现象,被称为物质的第五态,具有强相干性[1-2]。它不仅对基础研究有重要意义,而且在芯片技术、精密测量和纳米技术等领域,也都有很好的应用前景[3-4]。但其性质的研究需要多学科的参与,同时,BEC的各种性质需要实验与理论的结合,因此,在研究难度上有很大挑战[5]。文章中在国内外基础理论研究基础上,建立如下模型:即有三体复合效应时,讨论三势阱玻色爱因斯坦凝聚体系统隧穿动力学性质,采用了三模近似的方法,且在此基础上,结合数值分析的方法,期望研究结果可以引入更为丰富的动力学特性,为玻色-爱因斯坦凝聚体的基础性质探索奠定基础。
1 含三体复合项的三模近似
在这里的分析中,考虑三体复合的作用,即原子的损失主要来自非弹性三体复合-三个原子碰撞形成一个分子束缚态和另一个原子,粒子末态的动能使得它们从磁阱中逃逸出去。从而,凝聚体的粒子数减少。通常,这种非弹性三体复合损失导致在GP方程中包含与虚系数相乘的五次方项。因此,在GP方程中必须包含一个假设的三体项来描述复合耗散,通过调节s-波散射长度的值可影响三体复合率,三体复合率随a4增长。同样,对于一固定的填充项,从定态到周期的振荡态的转变可通过a的值来实现。
三势阱中有三体复合耗散及原子填充项存在时的GP方程被修改为如下形式,
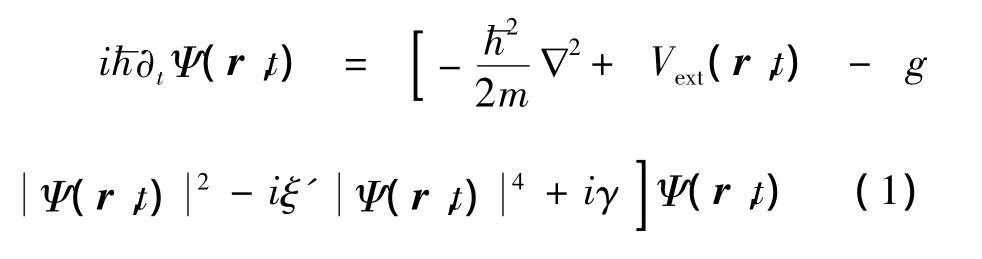
采用三模近似的方法来寻找方程(1)的解,

所以将方程(2)代入(1)后可达到下面的三个非线性方程
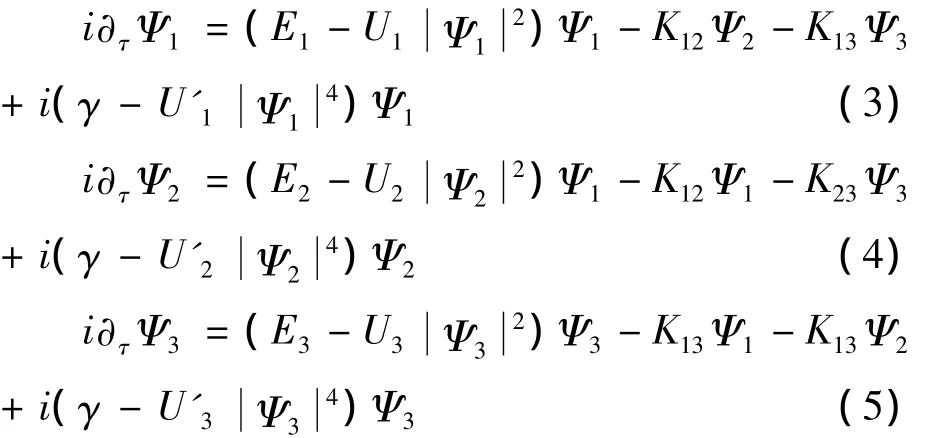
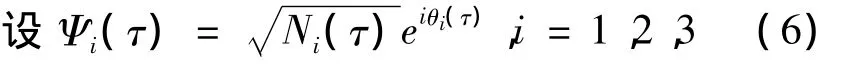
Ni(τ)是第 i阱中的粒子数,θi(τ)是 Ψi态的相,归一化的条件是N1+N2+N3=N,N是具有相同单位的三体凝聚体的粒子数。由以上条件,将方程(6)代入方程(3)-(5),其中Φ1=θ2-θ1,Φ2=θ3-θ1。为了了解三势阱中三体玻色-爱因斯坦凝聚体相互作用的新现象,仅考虑理想情况:即完全对称的情况。所以,令
U1=U2=U3=U,E1=E2=E3,阱1和阱2之间的粒子数差和阱2、3之间的相同,即N1-N2=N3-N2,且忽略1、3阱之间的作用,考虑第1、2阱之间的隧穿率等于第2、3阱之间的隧穿率,Φ1=Φ2=Φ,K12=K23=K,则上面的方程变为

2 零相位模式时三势阱凝聚体隧穿特性数值结果
使用数值分析的方法来研究宏观量子自俘获及三势阱中BEC在零相位时的振荡,众所周知,对于有相互吸引作用的85Rb,其散射长度满足a=-100a0,这里a0是玻尔半径。在目前的数值结果中,取as=-100a0,且通过改变A的值来改变散射长度a=Aas,在实验允许的范围内选取初始条件和物理参数为:N(0)=29,Z(0)=10,U=0.7A,K=3.9,γ =1.6 × 10-4,U'=0.05 ×10-4A4。
对于π =0,散射长度A逐渐减少时,方程(7)-(9)的数值结果展示于图1中。
在图1(a)中,A=3,非零的相对粒子数布局意味着系统处于宏观量子自囚禁态,这个现象在时间τ=3.5之前可以观察得到,展示在图1(a)的内部,随时间增大,相对粒子数Z在一个很小的负常数之间周期的振荡,这些现象也可以在0.63<A<3之间被观测到。在这个区域,Z最终会趋于一个负常数且系统会进入自俘获态。在图1(b)中,A=0.62,Z在一个负常数-10附近振荡。同时发现Z振荡时出现了量子拍现象,见图1(b)。平均相对粒子数仅在一个非零常数间跳跃意味着系统处于自俘获态,这种现象同样可以在区域0.585<A<0.62之间观察到,而当A<0.585时,系统展示了许多新特征。对于A<0.55,见图1(c),粒子数Z的幅度随时间递减,并且最终Z趋于一个负常数,但该负常数的绝对值递增,系统进入了很强的自俘获态,类似的现象也可以在区域0.505<A<0.55观测到,但是随A值减小,凝聚体进入完全自俘获态的时间被推迟,量子拍现象仍然会出现在这一区域,见插图1(c)。当继续减小A,如图1(d)所示,对于A=0.49,系统又周期的振荡于Z≈-10之间,这时阱之间的量子隧穿现象和量子拍现象同样出现了。图1展示了三阱中有原子填充和耗散时凝聚体的许多有趣特性,这意味着可通过Feshbach共振调节相互作用参数去控制系统在周期运动和定态间转化。

图1 π=0时不同A值下两阱中相对粒子数随时间变化
3 结 论
分析了在三势阱中三体复合耗散和原子云填充对耦合凝聚体的影响。在分析中,采用的是一种很简单的三模近似。通过这种方法,研究了修正的GP方程,并在对称阱的情况下得到了三个微分方程(7)-(9)。从理论上和数值上研究了这些方程,讨论了系统的定态和非定态特征。从数值上展示了三势阱间原子的非定态隧穿和一个阱中的自俘获。研究结果表明,随散射长度A的减小,势阱间原子的隧穿展示了高度的不对称特性且相对粒子数布居揭示了量子拍现象和共振特征。
众所周知,自俘获现象是由于原子间的非线性相互作用引起。不对称双势阱凝聚体中的原子分布展示了高度不对称,好像原子完全囚禁于一个势阱中。但对于三势阱中凝聚体的原子可以囚禁于任意一个阱中且最终达到自俘获态。最后,在自俘获和量子隧穿的过程中发现了量子拍现象和共振特征,但是这些现象在双阱中没有出现。
[1] Sadhan K.Adhikari.Coupled Bose-Einstein Condensate:Collapse for Attractive Interaction[J].Phys.Rev.A,2001,63:043611:1-5.
[2] E.Braaten,and H.W.Hammer.Three-body Recombination into Deep Bound States in a Bose Gas with Larger Scattering Length[J].Phys.Rev.A,2001,87(16):160407.
[3] Guan-Fang Wang,Li-Bin Fu,Jie Liu.Periodic Modulation Effect on Self-Trapping of Two Weakly Coupled Bose-Einstein Condensates[J].Phys.Rev.A.,2006,73:013619.
[4] Ju-Kui Xue,Ai-Xia Zhang,Jie Liu.Self-Trapping of Bose-Einstein Condensates in an Optical Lattice:the Effect of the System Dimension[J].Phys.Rev.A.,2008,77:013602.
[5] K.Nemoto,C.A.Holmes,G.J.Milburn,Quantum Dynamics of Three Coupled Phys.Rev.A,Atomic Bose-Einstein Condensates[J].2000,63:013604.
