基于MATLAB的麦弗逊悬架的优化

马网俊++张金伟

摘 要：本文建立了汽车振动和路面输入的数学模型，通过频域分析法研究了悬架刚度和阻尼对车身加速度、车轮相对动载荷和悬架动挠度的影响，综合安全性和舒适性考虑，利用MATLAB确定了麦弗逊悬架的最佳刚度和阻尼，从而确定了最佳的阻尼比。

关键词：麦弗逊悬架；MATLAB；阻尼比；优化

0 引言

汽车的振动是非常复杂的，对振动的研究中常常对其进行简化。

当悬挂质量分配系数接近1时，前后悬挂系统的垂直振动几乎是独立的[1]，所以可将模型进一步简化成车身与车轮两个自由系统的振动模型。

1 悬架系统数学模型

车身加速度、悬架弹簧动挠度fd和动载Fd/G相对于地面输入幅频特性。

取系统的平衡位置为坐标原点，设车身与车轮的垂直位移的坐标分别为z1和z2，麦弗逊悬架弹簧的刚度是K，阻尼是C，轮胎的刚度是Kt，汽车悬挂质量为m2，非悬挂质量是m1，可得运动方程：

（1）

（2）

通过以上的分析可以得到所建立的模型的车身对路面激励的幅频响应函数是：

（3）

式中：质量比；刚度比；阻尼比；频率比；w是此双质量系统的频率；wt是簧下质量系统的固有频率，；w0是只簧上质量振动时系统的固有率，；

。

车身加速度相对于地面的幅频特性是：

（4）

相对动载对的幅频特性是：

（5）

悬架动挠度fd对的幅频特性是：

（6）

2 麦弗逊悬架系统最佳阻尼匹配研究

由上述数学模型可知，对于悬架优化，簧上质量，非悬挂质量，轮胎刚度这几个参数是不会发生改变的。所以，我们以悬架弹簧刚度和阻尼系数为设计变量，对于悬架参数进行优化。

研究的悬架模型的簧上质量m2=400kg，非悬挂质量m1=40kg，轮胎刚度为kt=200kN/m。

（7）

同理可得：

假设路面为B级，车速为40m/s的条件下，根据公式（15）编写MATLAB的程序，可视化后可得图1。由图1可以清晰的看到车身加速度随弹簧刚度增大是不断减小的，随阻尼系数增大而减小，在阻尼系数最小值，刚度最大值时，车身加速度最小。换句话说，就是在此条件下，乘坐舒适性最好。

同理，在相同的条件下，根据（16）可以得到图4。由图4可以清晰的看到车轮动载荷随弹簧刚度增大是不断增大的，随阻尼系数增大也是不断增大的，在阻尼系数最小值，刚度最小值时，车轮动载荷最小。而车轮动载荷与汽车的行驶安全性有很大关系。

综合车轮动载荷和车身加速度两种情况，我们可以阻尼系数偏小，对于汽车的平顺性较好，对于弹簧刚度，可以通过优化来实现弹簧刚度的确定。

设计变量为弹簧刚度k2。

目标函数为兼顾路面车轮动载荷和车身加速度两者处在较佳情况，即目标函数为

式中为图3车身加速度中的最小值，Fd1为图4车轮动载荷中的最小值。

约束条件为15≤k2≤35

通过优化可得k2=25KN/m，从而可以得到阻尼比为ζ为0.25 。

3 阻尼比对车身加速度、车身动载荷和悬架动挠

度的影响

在其他条件不变的情况下，阻尼比的变化会对车身加速度、车身动载荷和悬架的动挠度产生影响，从而会影响汽车的平顺性和行驶安全性。下面保持质量比μ和刚度比γ不变，研究改变阻尼比ζ时，汽车车身加速度、车身动载荷和悬架动挠度的影响 ，以验证优化结果是否可信。

（1）阻尼比对于车轮相对动载荷的影响。设ζ=0.1、0.25、0.5，

在这三种情况下，根据公式（10），利用matlab计算，得到图3 。当阻尼比ζ变小时，车辆相对动载荷对于路面激励速度的幅频特性曲线相对剧烈，峰值都变大；阻尼比ζ变大时，曲线趋于平缓，但在低频和中频之间值最大，影响汽车安全性。

（2）阻尼比对于悬架动挠度的影响。由图4可以看出，在

高频区，阻尼比对于悬架动挠度的影响较小，且有明显下降，高阻尼对于悬架动挠度有利。

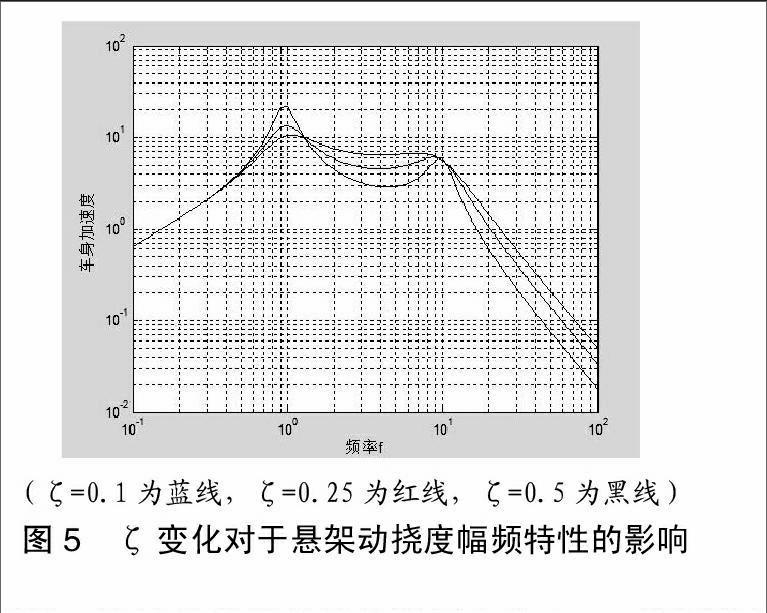
（3）阻尼比对于车身加速度的影响。由图5可以看出，在

高频区，阻尼比越大，车身加速度越大；而在低频区，三者变化很小，趋于一致；中频区域内，阻尼比增大，车身加速度有所上升。综合考虑，阻尼比0.25较好。

综上所述，该悬架模型的最佳阻尼比为0.25，重要结构参数k2=25KN/m，c=1500Ns/m 。

4 结语

本文从汽车平顺性入手，研究了悬架动挠度fd对于的幅频特性等几个幅频特性的特性，利用MATLAB的优化函数fmincon函数进行了优化寻优，得到了基于安全性和舒适性的最佳阻尼比，对于汽车研制和生产，有一定的价值。

参考文献：

[1]余志生.汽车理论[M].北京：机械工业出版社，2012.

[2]张志勇.精通MATLAB[M].北京：北京航空航天大学出版社，2012.

[3]耿雪霄，王昊君，郝凯明.基于MATLAB软件的麦弗逊悬架系统的阻尼匹配优化研究[J].湖南农机，2014，41（05）：56-58.endprint