堆石坝坝肩岸坡段防渗墙地震反应规律

董园林++邓锐敏++陈书燕

摘 要：以某堆石坝工程为背景，采用基于子模型法的三维非线性有限元对其右岸岸坡段防渗墙进行地震反应规律研究，采用薄层单元模拟各种接触面，坝体材料及覆盖层采用Hardin-Drnevich本构模型，分析得到岸坡段防渗墙与坝基防渗墙地震动力反应规律有较大差异。设计地震对岸坡段防渗墙的运行状态影响较大，考虑岸坡段防渗墙的抗震安全性是非常必要的。

关键词：岸坡段防渗墙 堆石坝 动力反应 子模型法

混凝土防渗墙是深厚覆盖层坝基上比较有效和经济的垂直防渗设施，诸多学者对坝基防渗墙的应力变形状态进行了深入探讨，但对岸坡段防渗墙应力变形状态研究较少。岸坡段防渗墙是对两岸坝肩覆盖层进行防渗处理的主要措施，其结构形式与坝基防渗墙差别较大，导致两者应力变形分布规律有较大差异。

某沥青混凝土心墙堆石坝最大坝高91.5m，坝址处河道基本顺直，河谷呈较为对称的“V”型。在坝轴线附近，现代河床位于河谷右岸，覆盖层厚35m～85m；左岸坝轴线处基岩裸露，右岸坡面局部见基岩出露，其余坡面则被第四系崩、坡积及泥石流混合堆积块、碎石夹粘土所覆盖，厚度18m～50m。场地地震基本烈度为7度。本文采用子模型技术对该沥青堆石坝岸坡段防渗墙进行了精细模拟，在三维非线性静力分析基础上，基于时程法对岸坡段防渗墙进行了地震动力计算分析，以揭示岸坡段防渗墙的静动力特性，从而对抗震安全性作出正确评价并为同类工程提供参考。

计算模型

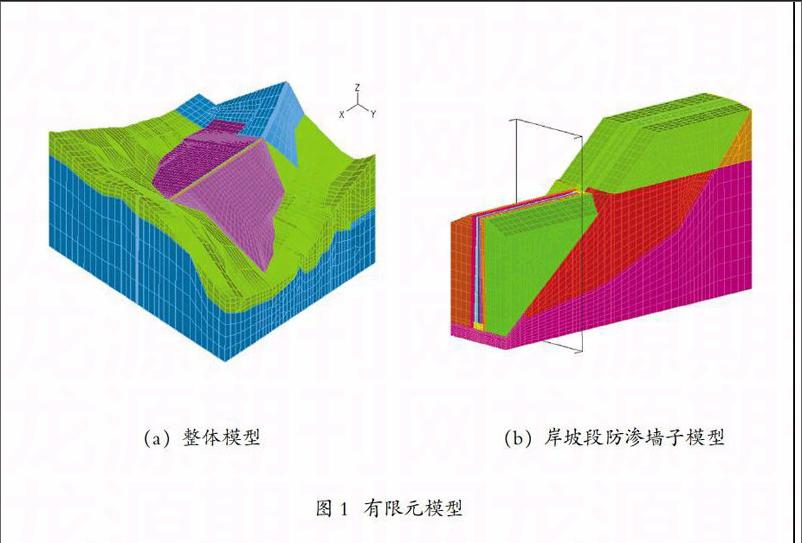
堆石坝岸坡段防渗墙、防渗墙上下游接触以及防渗墙与心墙之间的接头等多个细部构造与大坝整体结构尺寸相差十分悬殊，将其与大坝整体同时进行有限元计算分析具有一定的难度。因此有必要采用子模型技术以降低整体建模的难度以及提高关心部位结构的计算精度。图1为大坝有限元整体模型及岸坡段防渗系统子模型。其中有限元整体模型规模为39884个结点、38754个单元。岸坡段子模型中包括岸坡段防渗墙、部分防渗墙心墙以及防渗墙与心墙的接头等细部。该子模型由30425个结点、29348个单元组成。

基岩和混凝土均采用线弹性本构模型，且动弹模在静弹模的基础上提高30%，采用无质量地基。静力计算中基岩弹模取10GPa，泊松比0.3；岸坡段防渗墙及其接头弹模均取2.5GPa，泊松比0.167，密度2400 kg/m3。土石料和沥青混凝土的静力本构关系采用Duncan双曲线E-B模型，动力本构关系采用Hardin-Drnevich模型，防渗墙上下游侧的泥皮以及墙底残渣等各种接触面采用有厚度的动力薄层单元来模拟。

综合考虑坝址地区地质构造、潜在震源震级及震中距等因素，动力计算中选取Taft三向地震波进行分析。工程区地震动峰值加速度为0.15g，震动反应谱特征周期为0.45 s。

计算结果分析

1、岸坡段防渗墙加速度反应

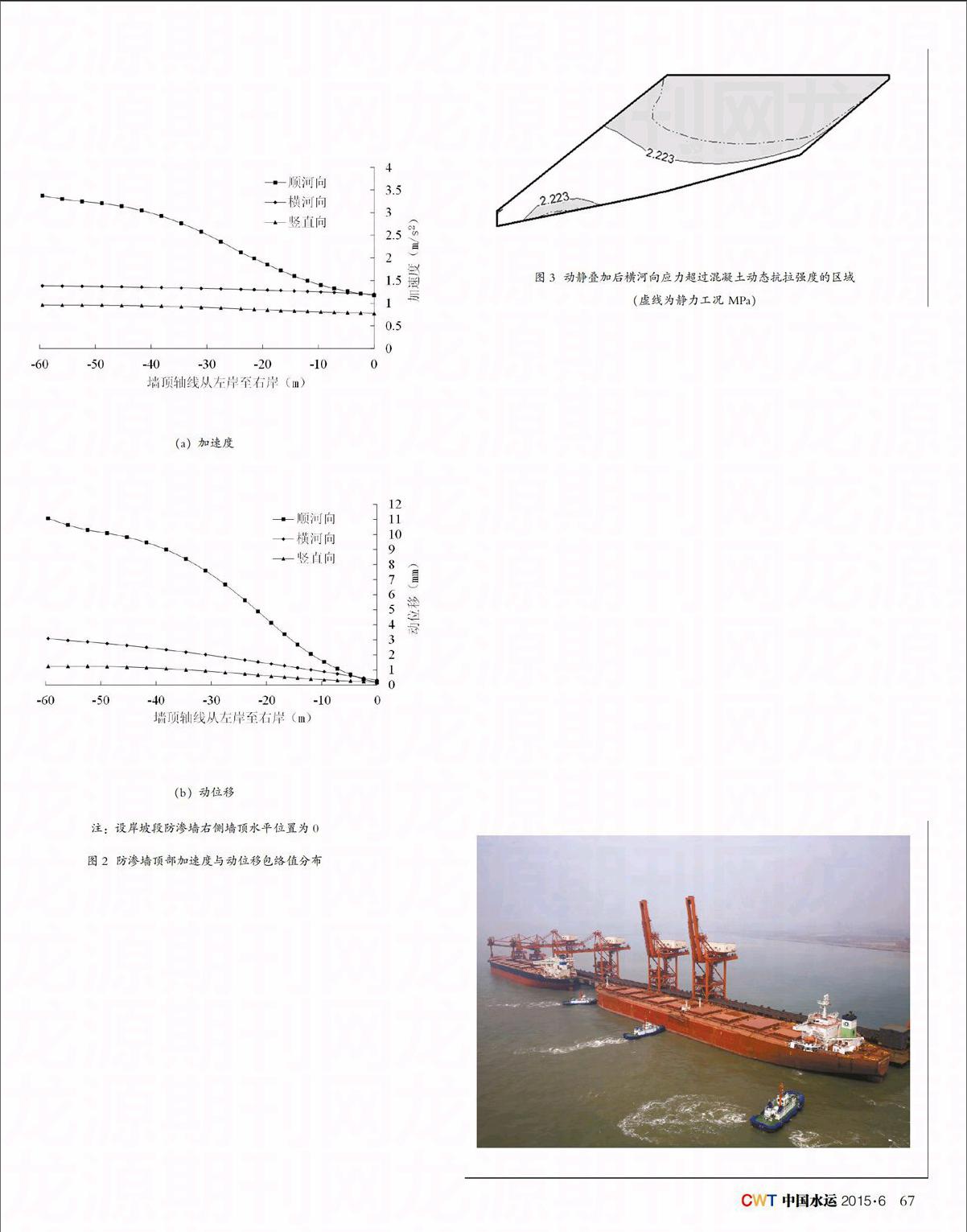
图2（a）为岸坡段防渗墙顶部加速度包络值分布曲线。在Taft波作用下，三个方向加速度反应由右侧向左侧逐渐增大，由于岸坡段防渗墙位置较坝基防渗墙高，但其位于右岸坝肩覆盖层中，故加速度反应较坝基防渗墙大且较沥青混凝土心墙小。

2、岸坡段防渗墙动力变形

图2（b）为岸坡段防渗墙顶部动位移包络值分布；由图可知，动位移反应由墙右侧到左侧逐渐增大，在防渗墙左侧墙顶附近动位移反应最大；由于河床中央坝体的沉降变形，将岸坡段防渗墙向河床中央拖拽，使得防渗墙整体有向左岸变形的趋势。

3、岸坡段防渗墙地震动应力

在Taft波的作用下，岸坡段防渗墙因为位于坝肩顶部，动应力反应较大。动静叠加后，防渗墙最大横河向正应力表现为全断面基本受拉，拉应力区域扩大，横河向最大拉应力由静力工况下的4.07 MPa增加为6.13 MPa，增幅达50.6%，出现在防渗墙右岸墙顶。图3为经动静叠加后防渗墙中心纵剖面横河向正应力超过C40混凝土动态抗拉强度2.223 MPa的区域。

结论

堆石坝岸坡段防渗墙位于右岸坝肩，动力反应较坝基防渗墙大。在Taft地震波作用下，加速度反应由防渗墙右侧向左侧逐渐增大，这与坝基防渗墙动力反应在河床中央最大的规律不同。

由于河床中央坝体的沉降变形，将岸坡段防渗墙向河床中央拖拽，使得防渗墙整体有向左岸变形的趋势，与坝基防渗墙横河向位移向河床中央收缩变形的规律不同。

动静叠加后，本工程案例中岸坡段防渗墙横河向拉应力超过C40混凝土抗拉强度的区域相对于静力工况增大，横河向最大拉应力较静力工况增幅达50.6%，局部区域增幅可达146%，因此应加强岸坡段防渗墙上部的配筋，并预埋灌浆管，以便于裂缝发生后进行灌浆封堵。

参考文献：

[1] 万彪，何蕴龙，熊堃.有厚度节理单元的开发与应用[J].水电能源科学，2008，26（4）：63-66.

（作者单位：四川省港航开发有限责任公司）endprint