抗滑桩计算理论及变刚度抗滑桩的应用

封露　蒋建平

摘 要：作为一种有效的工程措施，抗滑桩在边坡的加固工程、滑坡地质灾害防治中得到了广泛应用。然而，由于问题的复杂性，关于抗滑桩的工作机理、桩-土相互作用规律等问题并没有很好地解决，其设计理论与计算方法，还处于半经验半理论的不成熟阶段，目前对于单纯的抗滑桩加固边坡的研究已经无法满足可持续发展的要求，因此，抗滑桩的优化设计已是抗滑桩研究领域的一个新课题。该文主要从变刚度角度入手分析变刚度抗滑桩的应用，运用大型有限元分析软件ABAQUS分析变刚度抗滑桩加固边坡的作用机理。

关键词：变刚度抗滑桩 抗滑机理 ABAQUS 边坡加固

中图分类号：U41 文献标识码：A 文章编号：1672-3791（2015）02（a）-0199-02

滑坡的当前状态及其变化趋势的判断是滑坡防治方案选择中的关键问题之一。关于抗滑桩的计算理论，张永[1]曾提出三种常用的滑坡稳定性计算方法。第一，极限平衡法是在某种失稳模型条件下，假定滑坡为刚性体，对失穩分离面受力状态以及有效强度的研究，根据极限平衡原理，计算滑坡的稳定系数，并以此表征滑坡的稳定性[1]。第二，应力应变分析法与前者不同，它能充分考虑岩土的特性，也不对滑坡失稳分离面做任何假定，而是用计算所得的应力、应变分析失稳分离面的特征，识别滑坡变形破坏机制[1]。第三，模型试验方法是在工程地质勘探调查的基础上建立的滑坡物理地质模型及岩土体的力学模型，通过光弹、相似材料等试验，直观形象地再现滑坡变形破坏的发生和发展过程，但是要做到模型的几何、材料和力学等的全相似还存在一定的难度。

1 抗滑桩的计算方法

桩的内力分析计算可以分为以下2类。

1.1 弹性理论法

该法假定桩埋置于各向同性半无限弹性体中，并假定土的弹性系数为常数或随深度按某种规律变化。计算时将直径为d，长度为1的桩分为若干微段，根据半无限体中承受水平力并发生位移的Mindlin方程估算微段中心处的桩周土位移，另外根据细长杆（桩）的挠曲方程求得桩的位移，并用有限差分式表达。

1.2 极限地基反力法（极限平衡法）

极限地基反力法假定土处于极限状态，且地基反力的分布是事先假定好的分布形式。一般假定地基反力q仅为y的线性函数q=q（y），而与桩的挠度x无关。然后按照桩处于极限平衡状态下的平衡条件，计算出桩的最小锚固深度，进而按照地基反力的分布假定计算出桩的内力，再进行桩的设计。

2 抗滑桩抗滑机理及模型建立

2.1 抗滑机理

抗滑桩的抗滑机理是通过桩土之间的土拱、桩身反力、桩侧的摩阻力来抵抗滑坡推力[2]。该文建立了简单的三维桩土模型，研究了抗滑桩与边坡之间的土拱效应的形成机理和土拱效应沿桩身的变化情况。

2.2 ABAQUS有限元模型的建立[3]

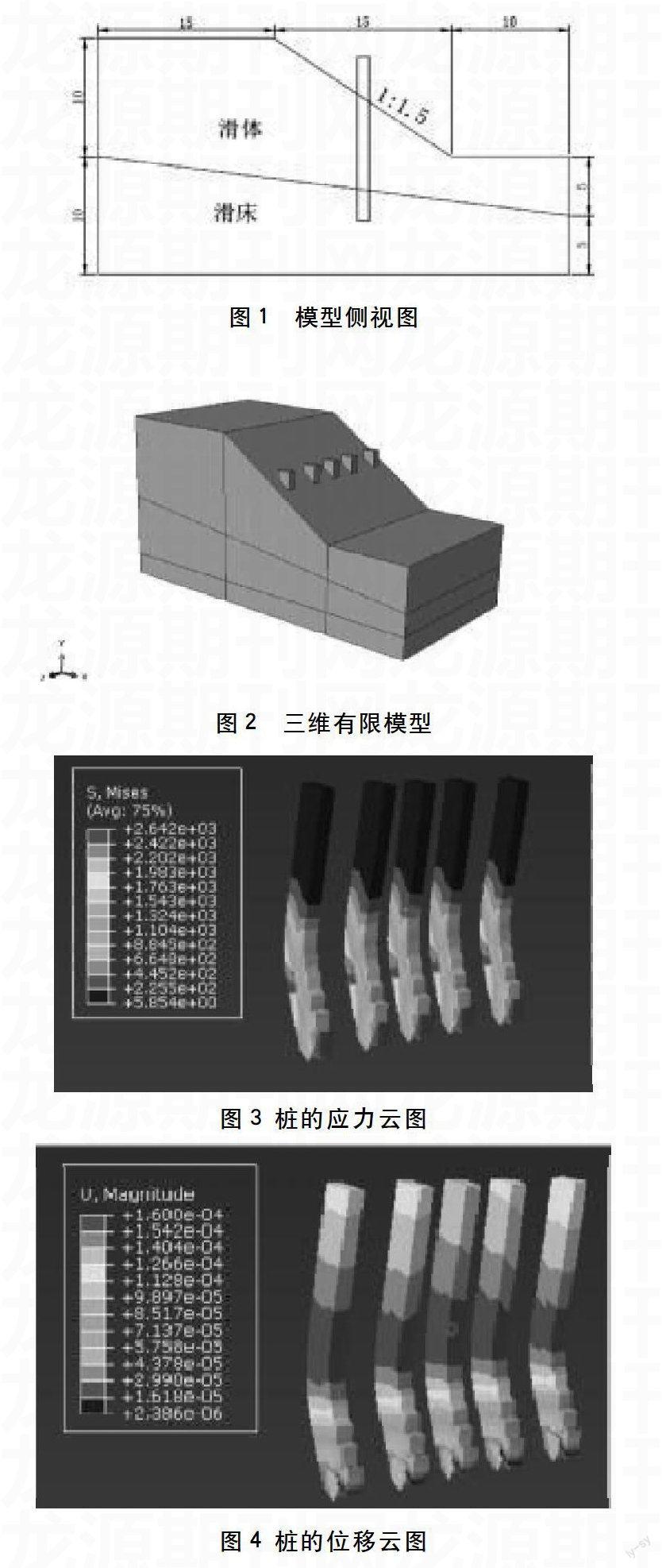
基于ABAQUS软件的三维有限元计算模型如图1所示。采用形状简单的边坡模型，坡高为10 m，坡度为1：1.5，坡顶距边坡后沿的水平距离为15 m，边坡后沿的上顶点距下顶点的垂直距离为20 m，边坡的宽度为20 m。选用矩形截面桩，长边为1.5 m，短边为1 m，桩长为14 m，抗滑桩加固在边坡的中部，桩心距坡脚的水平距离为7.5 m，桩底距模型底部2.5 m，桩和土均采用C3D8R实体单元。桩端与土采用绑定约束，桩土接触后不允许分离；桩侧与土采用面面接触。桩网格为0.5，土的网格为1。

3 计算结果分析

见图3、图4。

4 结语

以前对抗滑桩加固土坡的研究很少考虑滑坡推力空间分布的不均匀性，本文考虑滑坡的空间分布特征，即中间主滑面处的滑体要比两侧厚，主滑面的滑坡推力也明显大于两侧的滑坡推力。根据滑体厚度和滑坡推理空间分布的不均匀性，对抗滑桩进行变刚度布置。建立非等间距布桩加固边坡的三维模型，分析了上述布桩方式加固边坡的合理性。

参考文献

[1] 孙勇，张广栋.双排抗滑桩的机理及工程应用研究[J].矿业研究与开发，2008（5）：23-26.

[2] 张友良，冯夏庭.范建海，等抗滑桩与滑坡体相互作用研究[J].岩土力学与工程学报，2002，21（6）：839-842.

[3] 唐晓松，刘明维，叶海林.基于ABAQUS的抗滑桩三维有限元分析[J].地下空间与工程学报，2010（S2）：1614-1618.

[4] 费康，张建伟.ABAQUS在岩土工程中的应用[M].北京：中国水利水电出版社，2010.

[5] 蒋建平，张家得.抗滑桩合理桩间距的探讨[J].科技资讯，2014（1）.