下垫面变化条件下合河流域设计洪水修订

姚 成，孙如飞，李致家，刘开磊，张梦婕

(河海大学水文与水资源学院，江苏南京210098)

下垫面变化条件下合河流域设计洪水修订

姚 成，孙如飞，李致家，刘开磊，张梦婕

(河海大学水文与水资源学院，江苏南京210098)

基于新安江-海河模型，选取合河流域为研究对象，开展下垫面变化对设计洪水影响的研究。将合河流域的洪水系列分为1980年前、后两个部分，针对两个系列分别率定模型参数；再根据1980年后的参数来重新模拟1980年前的洪水，通过模拟出的次洪径流深和洪峰的变化幅度来反映下垫面变化对设计洪水的影响；同时，利用径流深的模拟结果修订设计洪水，并计算设计洪水的变化幅度。结果表明，合河流域的自由水蓄水容量和河网水消退系数均变大，流域的调蓄能力变大，设计洪水的洪峰值在减小；地下水过度开采与水利工程的建设是导致该流域设计洪水减小的主要因素。

新安江-海河模型；洪水模拟；下垫面变化；设计洪水修订；频率计算

随着经济社会发展，自然环境越来越频繁地受到人类活动的影响。1980年以来，海河流域受到人类活动的影响不断增强，流域下垫面发生了明显的变化，对水文资料的一致性产生较大的影响。在进行设计洪水频率计算时，对水文资料的可靠性、一致性和代表性有很高的要求，而下垫面的变化破坏了水文资料的“一致性”和“同分布性”。如何更加准确地对设计洪水进行一致性修订成为水文研究的一个重要内容，也是本文研究的重点。

设计洪水常用的修订方法包括常规分析法修订、水文模型[1]方法修订与经验公式法修订。与常规分析法相比，水文模型能够更好地模拟流域产汇流过程及考虑下垫面变化的影响。相比经验方法，模型方法的针对性与适用性更好，因而可得到较好的应用效果。本文选用新安江-海河模型模拟合河流域洪水过程，通过模型参数反映流域下垫面的变化情况；同时，利用模拟结果对合河流域设计洪水进行修订，并计算设计洪水的变化幅度，对修订成果进行了分析。

1 新安江-海河模型及流域概况

合河流域位于漳卫河流域上游，属于干旱半干旱地区，其流域控制面积为4 016 km2，多年平均降水量约600 mm。新安江模型在此流域的模拟效果较差，因此做了改进，得到新安江-海河模型。该模型在紫荆关以及阜平流域模拟结果[2]较好，说明模型可以应用到北方干旱半干旱地区。新安江-海河模型[3]包括蒸散发、产流、分水源和汇流4个模块，其中蒸散发和产流模块与新安江模型[4- 7]相同。分水源模块考虑地下水漏斗对降水产流的影响，在三水源划分模块中增加自由水补给深层地下水的部分(这部分由参数S0和F0来控制。其中，F0为补给深层地下水的渗漏率；S0为深层地下水的最大补给量)，从而分出4种水源。

整个海河流域秋冬季降雨较少，而工业、农业和生活用水量较多；北方用水来源又主要靠地下水的开采，当地下水开采量大于补给量时，就会造成地下水位下降。当严重超采时，就会造成地下水位的大幅度下降，形成地下漏斗。在产流计算时必须考虑到地下漏斗对径流过程的影响。这也是新安江-海河模型针对北方地下水特点做出的改进：当汛期来临时，地下水埋深较深，径流过程中地表水不断渗漏，补充地下水，抬升地下水位。新安江-海河模型将这样的情况概化成一个地下拦蓄水库，利用地下水库的调蓄作用来模拟这种现象。

2 模型应用及结果分析

新安江-海河模型的主要输入有降雨与蒸发两个部分，其中蒸发资料统一使用合河站的蒸发资料。面平均降雨量使用算术平均法计算，简单快捷而且精度也较高。

2.1 参数率定

将1958年～2011年合河流域的整个实测资料系列输入到新安江-海河模型中，对模型参数进行率定，实时观察模拟结果。在率定的过程中发现，1980年前后模型对洪水模拟的精度差异明显。结合对合河流域的累积降雨P与累积径流深R的关系曲线的研究，以及关于海河流域下垫面变化的研究成果[2]，选择1980年作为分界点，对合河流域1958年～2011年的实测资料进行分段研究，探求其模拟结果有明显差异的原因。在1958年～1980年期间选择了18场洪水；在1981年～2011年期间选择了28场洪水，利用新安江-海河模型分别对不同时间段的洪水进行模拟分析。

根据合河流域的自然特征，设定参数初始值，并保持非敏感参数不变，在参数率定的过程中调整敏感参数值。根据合河流域实地调研，不考虑气候变化的因素，并参考海河流域相关研究成果[8- 14]，本文着重研究下垫面变化条件下流域自由水蓄水容量SM以及河网退水系数CS的变化情况，参数的率定结果见表1。

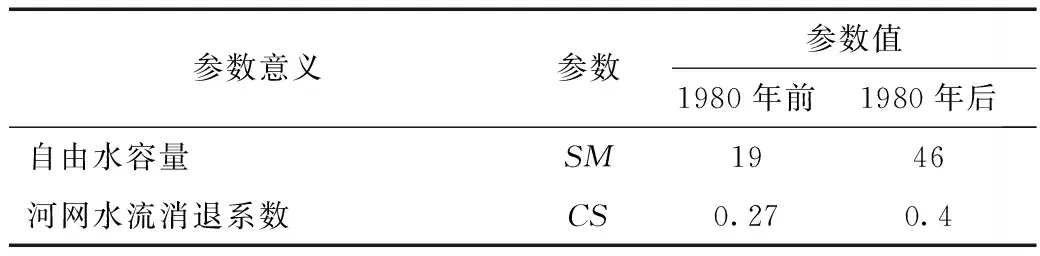
表1 合河流域1980年前后新安江-海河模型参数率定结果

表1的结果表明：在其他参数不变的情况下，流域自由水蓄水容量SM和河网退水系数CS都在变大，说明合河流域下垫面条件变化后，流域的调蓄能力在变大。结合合河流域20世纪80年代以后的发展状况以及相关实测资料，可以分析其发生变化的原因：①1980年后的流域的地下水开采量不断地增大，超过了地下水的补给量，导致地下水位下降，部分地区形成地下漏斗，而且这些地下漏斗有逐年扩大的趋势，进而引起整个流域渗漏量急剧增加；②流域内修建的大中小型水库变多，各类塘坝数量也在增多，地表的填洼量增大，导致流域的调蓄能力增强，参数SM和CS变大。

2.2 模型合理性检验

利用确定性系数作为洪水过程与实测过程之间的吻合程度的指标，来检验新安江-海河在合河流域适用的合理性。即

(4)

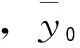
表2 确定性系数DC计算结果

由表2结果知，确定性系数DC=0.88。根据洪水预报精度评定等级标准[17]，当0.9>DC>0.70时，项目预报等级达到乙级标准，说明新安江-海河模型在合河流域具有很好的适用性。

2.3 结果分析

对1958年～2011年的模拟结果进行误差统计分析[16]，得到1980年前后径流深R和洪峰Q误差统计结果(见表4)。

表3 新安江-海河模型径流模拟过程 mm

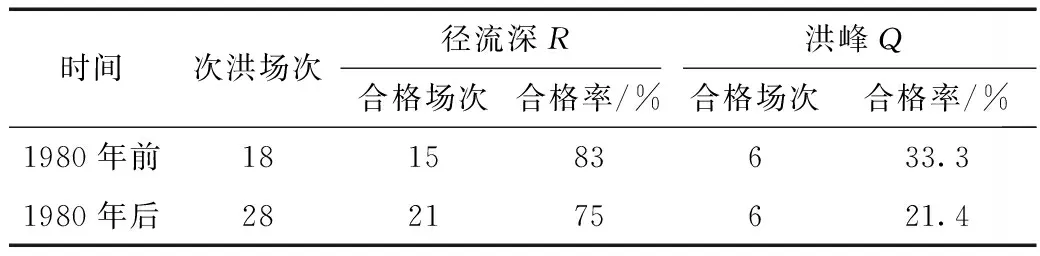
表4 合河流域洪水模拟误差统计

表4结果显示，径流深R的模拟结果较好，而洪峰流量Q的模拟结果较差。1980年前后径流深R的合格率平均达到了80%，远远高于洪峰流量Q。径流深R的合格率超过了70%，达到了乙级标准[17]，模型参数率定的精度较高。洪峰的模拟结果较差的原因分析：由于所选的洪水中包括较多场次的小洪水，小洪水其过程的比较复杂，洪水过程难以模拟，与大洪水一起模拟时导致整体的洪峰模拟精度下降，合格率不高。在以后的研究中，将针对大中小不同类型洪水，展开更深入的研究。

3 设计洪水修订与频率计算

1980年前后合河流域下垫面条件发生了明显的变化，水文资料的一致性被破坏。为了推求设计洪水，需要对整个洪水系列进行一致性修订。考虑到径流深R的模拟结果较好，平均合格率较高，选择R的模拟结果来对洪水的一致性进行修订。

合河流域的洪水修订主要是针对洪峰流量Q、5日洪量W5、15日洪量W15和30日洪量W30。本文以利用径流深R的模拟结果修订设计洪水洪峰Q为例，探究设计洪水的修订方法选择。

3.1R～Q相关关系分析

选择合河流域1958年～2011年的实测径流深R以及实测洪峰流量Q资料，分析R与Q的相关关系(见图1)。

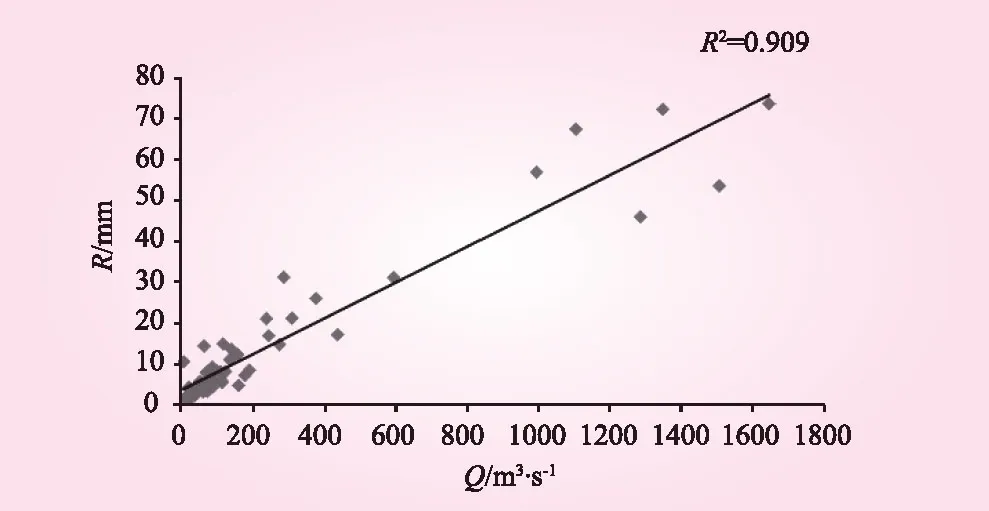
图1 实测径流深R与实测洪峰流量Q相关关系曲线

由图1可分析得出，实测径流深R与实测洪峰流量Q存在线性相关关系，计算其相关系数R2=0.909。通常情况下，|R2|>0.8时，认为两个物理量存在很强的线性相关关系。结果表明：在合河流域径流深R与洪峰流量Q存在很好的线性相关关系，利用径流深的预报结果来修订洪峰是合理可行的。

3.2 归一化法

归一化方法有两种形式，一种是把有量纲表达式变为无量纲表达式，一种是把数变为(0，1)之间的形式。前一种形式是归一化的基本核心概念，后一种是为了计算的方便而提出来的。

本文同时应用了归一化方法的两种形式，分别将R与Q归一化到(0，1)区间，然后进行设计洪水的修订计算。

3.2.1 归一化方法应用

利用归一化方法将径流深R无量纲化，具体的过程如下：

(1)将1980年后的参数代入到1980前进行模拟计算，得到新的一组模拟结果；将两组模拟结果进行比较计算，得到每一场洪水的径流深预报值RP的相对变化幅度

Φ=(RY2-RY1) /RY1

(5)

式中，RY1为1980年前参数模拟的径流深预报值，mm；RY2为1980年后参数模拟的径流深预报值，mm。

(2)列出1980年前实测径流深R的系列值，找出其中最大值RMAX，将每一个系列值归一化，即求出每一场洪水的实测径流深R的相对值

α=R/RMAX

(6)

(3)归一化后的相对修订幅度Φ与相对实测径流深α的取值区间都是(0，1)，在直角坐标系上点出所有坐标点(Φ，α)，并做出一条相关关系曲线，图2为Φ-α的相关关系曲线。

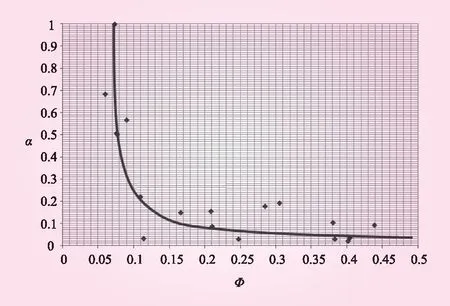
图2 相对修订幅度Φ与相对实测径流深α相关关系曲线

3.2.2 曲线拟合程度分析

为了表征图2中相关关系曲线对离散点的拟合程度，本文计算对应的点到相关关系曲线的最短距离L，其中负值表示点在曲线的左下方，正值表示点在曲线的右上方，零代表点在曲线上。统计结果见表5。

表5 离散点统计结果

由表5可计算得：离散点距离相关关系曲线的最短距离L的平均值为LAV=0.033。18个离散点中有4个位于曲线上，7个点位于曲线的下方，7个点位于曲线的上方，从离散点的分布情况看，相关关系曲线进过离散点点群中心。再从定量层次分析，代入符号计算最短距离L的平均值LAV1=0.004 8。由图2可知，相对修订幅度Φ的读数精度为0.005，即LAV1<0.005。这说明逼近曲线与离散点的平均偏离程度是小于相对修订幅度Φ的精度，因此图2中相关关系曲线对离散点的拟合程度是满足精度的。

3.3 设计洪水修订计算

合河流域洪水修订时间为1953年～1980年，为求洪峰流量Q的修订幅度μ，需将Q归一化。即

β=Q/QMAX

(6)

式中，β为相对洪峰流量值，β=0～1；QMAX为洪峰流量最大值，m3/s。

归一化后的相对洪峰流量值β对应于图2中的纵坐标相对径流深α，根据计算出的β系列值，在曲线上找到每一个对应点的横坐标值，即为所求的μ值，并利用式(7)计算出Q的修订值

Q修=Q×( 1-μ)

(7)

合河流域1953年～1980年的洪峰修订成果见表6。表6的结果表明：①1980年前的洪水修订幅度最大值为50%，最小值为7%；②洪水的修订幅度大小与洪水大小成负相关关系，即大洪水的修订幅度小，小洪水的修订幅度大。分析发现，对于大洪水年份，下垫面变化对洪水的影响效果不明显，汛期开始初期，地下水得到迅速补给。补给量大于了开采量，使得地下水位上升；同样地，地表的水库、塘坝、沟壑也得到迅速的补给，因而流域的调蓄能力只能在初期起作用，后期基本不起调蓄作用。所以，大洪水年份的Q修订幅度都比较小；而对于小洪水年份，来水较少，地下水和地表水的补给速度没有那么迅速，整个汛期的流域调蓄作用一直起着较大作用。因此当下垫面发生变化后，对小水年份的影响非常明显，洪峰Q的修订幅度较大。

表6 洪峰流量Q修订成果

3.4 设计洪水频率计算

根据得到的1980年前洪峰修订值Q修，与1980年后的洪峰值Q组成完整的洪峰新系列(1953年～2011年)，分别对修订前以及修订后的洪水系列进行频率计算，并列出不同频率下的洪峰流量以及对应的特征参数(见表7)。

表7 合河流域设计洪水修订成果

由表7中结果得，合河流域1980年后，由于下垫面的变化导致其设计洪水洪峰值减小，减小的平均幅度为5%左右，减小幅度随着设计频率的增大而增大。根据表7的结果，百年一遇的洪水洪峰减小幅度为3.5%，由原来的2 308 m3/s减少到2 227 m3/s，十年一遇的洪水减小幅度为6.5%，洪峰值相由798 m3/s减少到746 m3/s。根据GB/T 22482—2008《水文情报预报规范》中的标准，表7中设计洪水洪峰的减少幅度属于正常情况，不会对流域造成安全隐患。

4 结 语

20世纪80年代以后，海河流域由于受到剧烈的人类活动影响，导致1980年前后合河流域的下垫面发生了明显的变化。为了研究下垫面变化对设计洪水[18]的影响，在洪水模拟的过程中将实测资料分成1958年～1980年和1981年～2011年两个时间段，分别对这两个部分进行参数率定。 将率定好的1980年后的参数代入1980年前重新模拟，得到新的模拟报结果，然后利用归一化方法对洪水的一致性进行修订，最后进行设计洪水频率计算。

由修订结果可以看出：①大洪水的修订幅度小，小洪水的修订幅度大；②固定频率下的设计洪水，修订后比修订前的值要小，减小幅度为5%左右，并且随着设计频率的增大而减小。分析显示，合河流域下垫面条件在1980年前后发生了明显变化，引起了设计洪水洪峰值的减小。对于大洪水而言，下垫面变化对设计洪水的洪峰影响效果并不明显；但是对小洪水的影响效果就相当明显，小洪水洪峰的减小幅度达到了50%。

[1]陈红刚， 李致家， 李锐， 等. 新安江模型， TOPMODEL和萨克拉门托模型的应用比较[J]. 水力发电， 2009， 35(3)： 14- 18．

[2]李致家， 于莎莎， 戴建男， 等. 利用水文模型研究下垫面变化对洪水的影响[J]. 人民黄河， 2012， 34(7)： 17- 19．

[3]李致家， 黄鹏年， 张建中， 等. 新安江-海河模型的构建与应用[J]. 河海大学学报： 自然科学版， 2013， 43(3)： 189- 195．

[4]赵人俊. 流域水文模拟新安江模型和陕北模型[M]. 北京： 水利电力出版社， 1984．

[5]李致家. 水文模型应用与研究[M]. 南京： 河海大学出版社， 2008．

[6]芮孝芳. 水文学原理[M]. 北京： 中国水利水电出版社， 2004．

[7]何长高， 董增川， 陈卫宾. 流域水文模型研究综述[J]. 江西水利科技， 2008， 34(1)： 21- 25．

[8]李致家， 周赛， 姚玉梅， 等. 经验方法研究下垫面变化对洪水的影响[J]. 湖泊科学， 2012， 24(4)： 637- 642．

[9]邬龙， 何长宽， 徐世宾， 等. 大清河流域下垫面变化对设计洪水的影响[J]. 华北水利水电学院学报， 2011， 32(3)： 1- 3．

[10]KUMAR S， MERWADE V. Impact of watershed subdivision and soil data resolution on SWAT model calibration and parameter uncertainty1[J]. JAWRA Journal of the American Water Resources Association， 2009， 45(5)： 1179- 1196．

[11]TRIPATHI M P， RAGHUWANSHI N S， RAO G P. Effect of watershed subdivision on simulation of water balance components[J]. Hydrological processes， 2006， 20(5)： 1137- 1156．

[12]水利部海河水利委员会. 海河流域下垫面变化对洪水影响研究[R]. 天津： 水利部海河水利委员会， 2009．

[13]韩瑞光. 大清河山丘区下垫面变化对洪水径流影响问题的研究[D]. 天津： 天津大学， 2009．

[14]李建柱， 冯平. 紫荆关流域下垫面变化对洪水的影响[J]. 地理研究， 2011(5)： 921- 930．

[15]董国强， 杨志勇， 于赢东. 下垫面变化对流域产汇流影响研究进展[J]. 南水北调与水利科技， 2013， 11(3)： 111- 117．

[16]李致家， 菅瑞卿， 薛清敏， 等. 洪水预报误差置信限与误差评定方法研究[J]. 河海大学学报： 自然科学版， 2005， 33(1)： 32- 35．

[17]包为民. 水文预报[M]. 北京： 中国水利水电出版社， 2009．

[18]李致家， 董增川， 梁忠民， 等. 大流域洪水预报与洪水调度管理方法研究[J]. 水力发电， 2004， 30(1)： 12- 15．

(责任编辑 陈 萍)

Study of the Effect of Underlying Surface Change on Design Floods of Hehe River Basin

YAO Cheng, SUN Rufei, LI Zhijia, LIU Kailei, ZHANG Mengjie

(College of Hydrology and Water Resources, Hohai Univercity, Nanjing 210098, Jiangsu, China)

The Xinanjiang-Haihe model is applied to assess the effect of underlying surface change on the design floods of Hehe River Basin. The flood events are separated into two periods bounded by the year of 1980. The parameters of Xinanjiang-Haihe model are calibrated for these two split periods respectively. Then, the flood events before 1980 are simulated again by using the parameter values for the period after 1980. The runoff and peak simulations are analyzed to evaluate the influence of underlying surface change on design floods. Additionally, the simulated runoff results are used to revise the design floods. The variation ranges of design floods are also calculated as well. The results indicate that the values of free water capacity and recession constant for the latter period are larger than that for the former period, the capability of flood storage of Hehe River Basin has increased after 1980, and the design flood peaks have decreased after 1980. The major reasons may be the over-exploitation of groundwater and hydraulic engineering construction．

Xinanjiang-Haihe model; flood simulation; underlying surface change; revision of design flood; frequency calculation

2015- 02- 10

国家自然科学基金(41130639，41101017，51179045，41201028)；水利部公益性行业科研专项经费项目(201401034)

姚成(1982—)，男，江苏扬州人，副教授，博士，主要从事水文预报研究．

TV122

A

0559- 9342(2015)11- 0009- 05