分形几何在致密砂岩储层微观孔隙结构研究中的应用——以苏里格气田东南部上石盒子组盒8段为例

杨 海，孙 卫，明红霞，霍 磊

(1.大陆动力学国家重点实验室，陕西西安 710069；2.西北大学地质学系)

分形几何在致密砂岩储层微观孔隙结构研究中的应用
——以苏里格气田东南部上石盒子组盒8段为例

杨 海1，2，孙 卫1，2，明红霞1，2，霍 磊1，2

(1.大陆动力学国家重点实验室，陕西西安 710069；2.西北大学地质学系)

致密砂岩储层孔隙结构在一定尺度内具有统计自相似和分形特征。利用分形几何原理，结合压汞测试，建立了毛管压力曲线求取分形维数的方法，探讨了致密砂岩孔隙结构的分形特征,分析了储层物性及孔隙结构各类参数和分形维数之间的关系，进一步明确了孔隙结构分形维数可综合反映孔隙空间复杂程度的地质意义。结果表明,只有当孔隙半径大于趋势线拐点所对应的孔隙半径时，致密砂岩孔隙结构才具有分形特征，分形维数介于2.0～2.3。分形维数越大，致密砂岩孔隙结构复杂程度越高，非均质性越强。

苏里格气田；盒8段；致密储层；孔隙结构；分形维数；毛细管压力

分形是对那些没有特征长度但又具有自相似性的图形、构造及现象的总称，分形理论即是利用分形元，从整体上研究在任何尺度下都具有精细分形结构的性质和规律[1]。前人研究认为多种地质现象都具有分形特征，并利用分形理论研究了地表形态和含油气构造的分布、断层体系和沉积相带的划分、矿产分布与储量的表征等方面[2-3]。

储层微观孔隙结构的研究包括对孔喉大小、分布及形态不均一性的表征和描述[4-5]。目前已经提出诸如孔隙度、渗透率、孔喉比、孔喉半径平均值、孔喉配位数等多种孔隙结构参数，定性描述了孔隙结构的分布特征，并建立了储层各种物性参数的关系，但还有诸多不足[6-7]。砂岩作为一种分形结构，其孔隙结构在一定的尺度范围内具有分形性质[8]，因此分形维数成为定量描述微观孔隙规律性结构与组合特征的重要参数，并可定量评价储层微观非均质性[9-11]。

本文根据高压压汞资料，利用分形几何理论及岩石孔隙分布的分形几何模型，测定了孔隙结构的分形维数，并建立出储层孔隙结构参数与分形维数的定量关系，从地质学角度解释了分形维数的意义。

1 孔隙大小分布的分形模型

分形几何的研究对象是不规则几何形态中具有某种统计自相似性的现象，分形维数是分形空间内最基本的特征量[12]。

天然多孔岩石孔隙与喉道的分布具有统计自相似性，因此可利用Mandlbrot的几何维数方法进行孔隙结构的分形描述，孔隙大小分布函数与孔隙分布分形维数的关系如下[13]：

(1)

式中，N是分形集合体中孔隙半径大于和等于r的孔隙数目；P(r)是孔隙半径分布密度函数；D是孔隙分布分形维数;α是比例常数。

光滑三维孔隙空间类似于一个线度为r、覆盖个数为n的球体，其体积V的计算公式为：

V=nr3=mr3-D

(2)

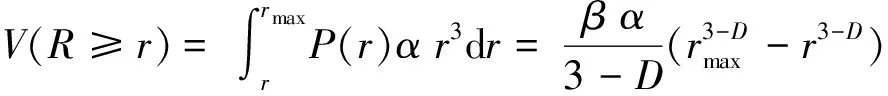
(3)

则储层的总孔隙体积为：

(4)

将(3)、(4)代入孔径大于r的孔隙累积体积频率S′中得：

(5)

对于微观孔隙非均质性强的储层，rmin≪rmax，因此孔径小于r的孔隙累积体积百分数S的表达式为：

(6)

式(6)即为储层孔隙大小分布的分形模型。二维平面内D为0～2，三维空间内D为0～3[14]。

2 利用毛管压力曲线测定孔隙结构的分形维数

对于三维空间孔隙结构的分形维数的计算，需要借助一种能够进入孔隙空间的结构元素，通过统计不同半径孔隙中元素的数目，来得到分形维数[15-16]。

在压汞实验中，水银进入不同半径孔隙的难易程度可以通过毛细管压力的大小来反映，由此得到的毛细管压力曲线可以作为计算三维空间孔隙结构分形维数的基础数据。与储层微观性质相关的全部参数，诸如孔隙度、渗透率、孔隙喉道大小分布、孔喉比等，都可以利用毛管压力资料获得。

由压汞测试的过程可知，在某一压力下进入岩样的汞的体积等于该压力对应的连通孔隙和喉道体积之和。据此原理推导分形维数的计算过程如下[17-18]：

假设以r为测量尺度对某储层岩石样品进行测度，所测出的半径为r的孔隙数量为N(r)，两者之间关系如下：

N(r)∝r-D

(7)

毛细管模型中：

N(r)=VHg/(πr2l)

(8)

式中，l为毛细管的长度，VHg为水银流经半径为r的毛细管时所对应的累计体积。

由式(7)、式(8)可得：

VHg/(πr2l)∝r-D

(9)

VHg∝r2-D

(10)

将毛管压力计算公式Pc=(2σcosθ)/r代入式(10)得：

VHg∝PcD-2

(11)

式中，Pc为毛细管压力；σ为界面张力；θ为接触角。

将岩样中汞饱和度的计算公式SHg=VHg/Vp代入式(11)中得：

SHg=αPcD-2

(12)

式中，SHg为汞饱和度；Vp为样品孔隙总体积；α为常数。

对式(12)两边取对数得：

lnSHg=(D-2)lnPc+lnα

(13)

式(13)说明如果储层岩样的三维孔隙结构具有分形性质，则汞饱和度与毛管压力在双对数坐标中呈线性关系，根据直线的斜率即可求得分形维数D。

需要说明的是J函数也可求取孔隙结构的分形维数。

3 苏里格气田东南部上石盒子组盒8段储层孔隙结构的分形特征

砂岩孔隙结构是控制储层物性及含油性的主要因素，由岩心和压汞资料统计分析可知，只有当r小于某一孔隙半径时，储层岩样的孔隙才具有分形结构，孔隙结构表现为统计自相似性特征[12]。三维欧氏空间内孔隙结构分形维数应介于2～3，如果分形维数大于3，则说明该孔隙在该尺寸范围内不具有分形结构[19-20]。

苏里格气田东南部上石盒子组盒8段为典型的低孔低渗致密储层。统计研究区15口井18个样品的压汞资料，忽略实测压汞曲线中不能反映岩石孔隙结构的初始段，利用上述方法分别作出lnSHg～lnPc的拟合关系，并计算了每个样品的分形维数。结果表明，并不是所有范围内lnSHg～lnPc都具有线性分形特征，即不是所有尺度的岩石孔隙都具有分形结构，分形结构的尺度存在下限。以J42-21井为例(图1)，开始出现直线段时的孔隙半径为1.022 μm，对应的毛细管压力0.719 MPa，累计进汞饱和度4.7%，在孔隙半径为0.406 μm时出现拐点，拐点之下尽管lnSHg～lnPc也呈直线关系，但分形维数大于3，因此该尺度范围内孔隙不具备分形结构特征，只有当孔隙半径大于趋势线拐点所对应的孔隙半径时，孔隙结构才具有分形特征。这是因为毛管压力或汞饱和度的大小受孔隙大小的控制，孔隙半径越小，毛管压力值越大，汞饱和度越低，小孔隙的分形维数大，孔隙结构复杂，分形特征明显或不具备分形特征。

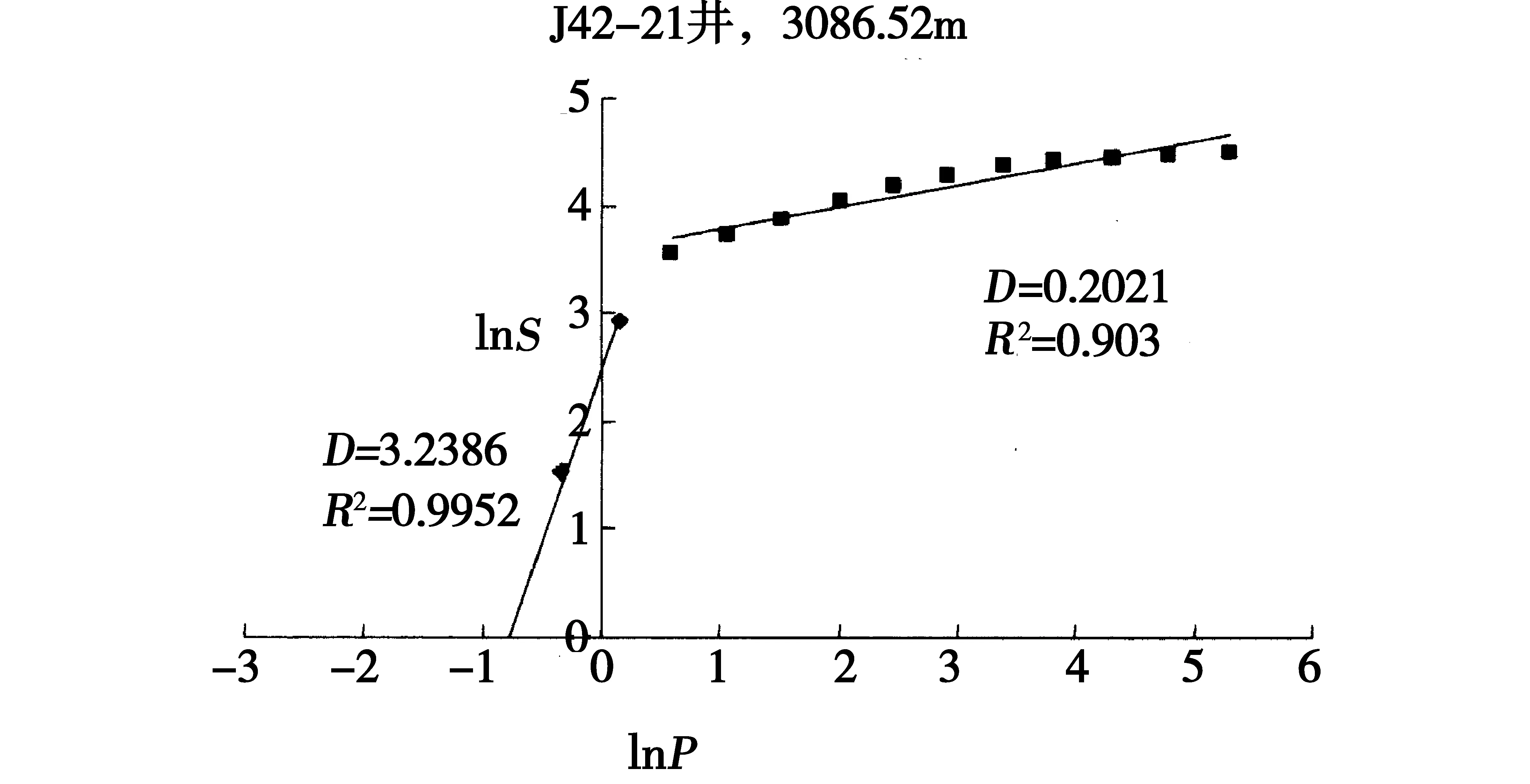
图1 毛管压力曲线求取分形维数

研究区目的层分形维数值介于2.0～2.3(表1)，相关系数均大于0.8，其结果是可信的。

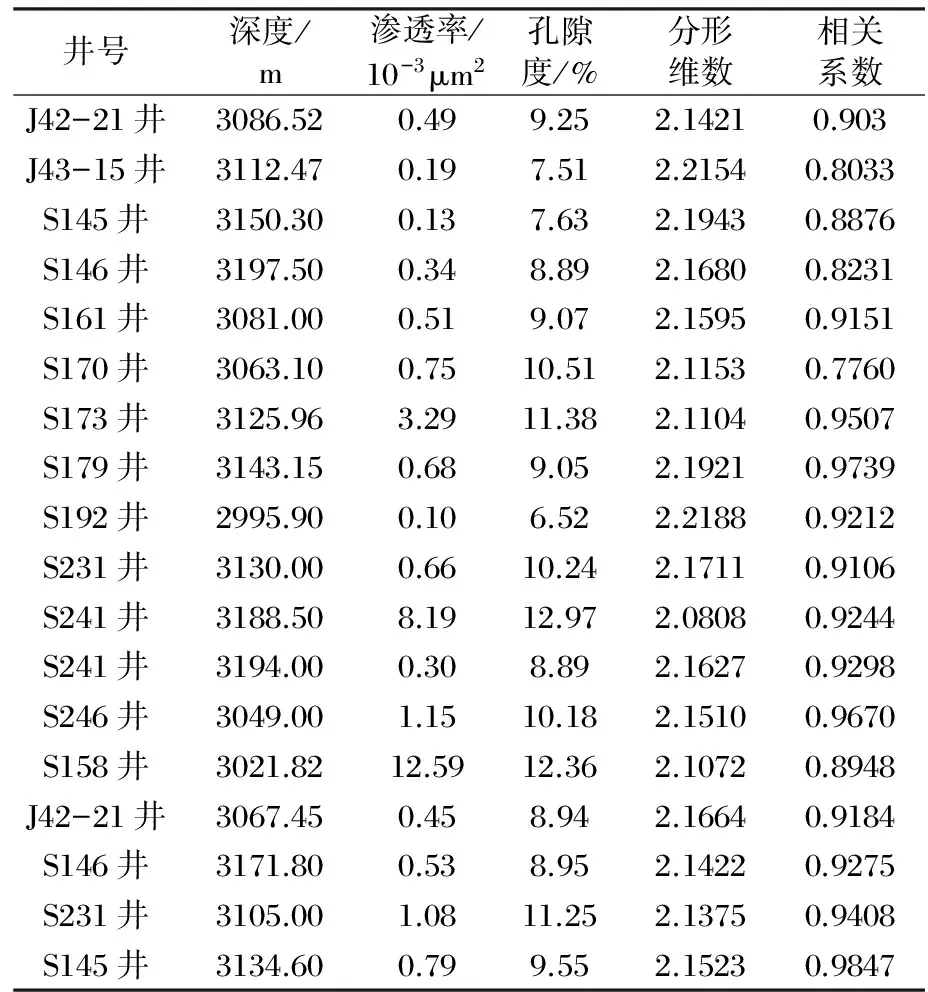
表1 研究区盒8段储层岩样物性参数与分形维数

4 孔隙结构分形维数的地质意义

数学上分形维数能反映所研究对象的空间复杂性，推断地质上分形维数能定量表征孔隙结构的复杂程度，进而体现储层物性、渗流性及含油性特征[21]。

4.1 储层物性与分形维数

储层物性除与岩石本身性质有关外，还受孔隙结构复杂程度的影响，包括孔隙表面粗糙程度、分布、形状及连通性等[22-23]。由图2可知,分形维数与孔隙度、渗透率整体上呈负相关：分形维数越小，孔隙喉道表面越光滑，孔隙分布越均匀，连通程度越高，孔隙度、渗透率越大，储层储集性能和渗流能力越好；随着分形维数的增大，储层非均质性逐渐增强，孔隙度、渗透率降低，储层储集性能和渗流能力变差。

4.2 孔隙结构参数与分形维数

4.2.1 孔喉大小参数与分形维数的关系

(1)排驱压力和中值压力。排驱压力是指非润湿相开始进入岩样最大喉道时所需要的最低压力，中值压力则指非润湿相饱和度为50%时所对应的毛管压力值。二者大小与储层物性(特别是渗透率)密切相关，是评价储层储集能力和渗滤性能的重要参数之一。排驱压力小，说明非润湿相进入岩样最大连通孔喉时所需要的启动压力小，储层物性好；反之，储层物性差。研究区分形维数与排驱压力、中值压力都呈正相关关系(图3、图4)。排驱压力和中值压力越小，分形维数越小，对应的储层物性相对较好，相同地质条件下岩石的渗滤能力强；小孔隙内，由于排驱压力高，溶蚀流体难以进入，分形维数大。与前述结果分析一致。

图2 储层物性与分形维数的关系

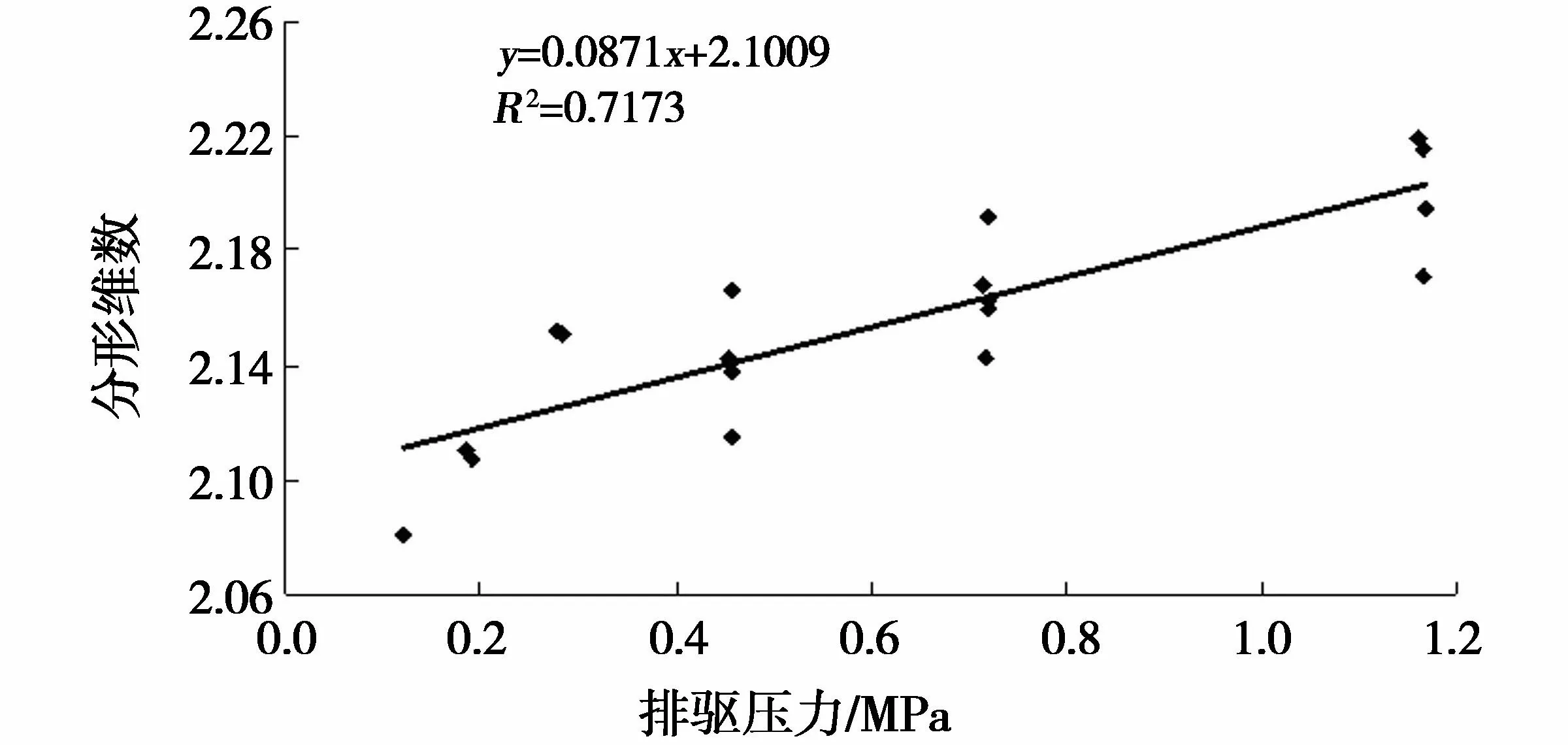
图3 排驱压力与分形维数的关系

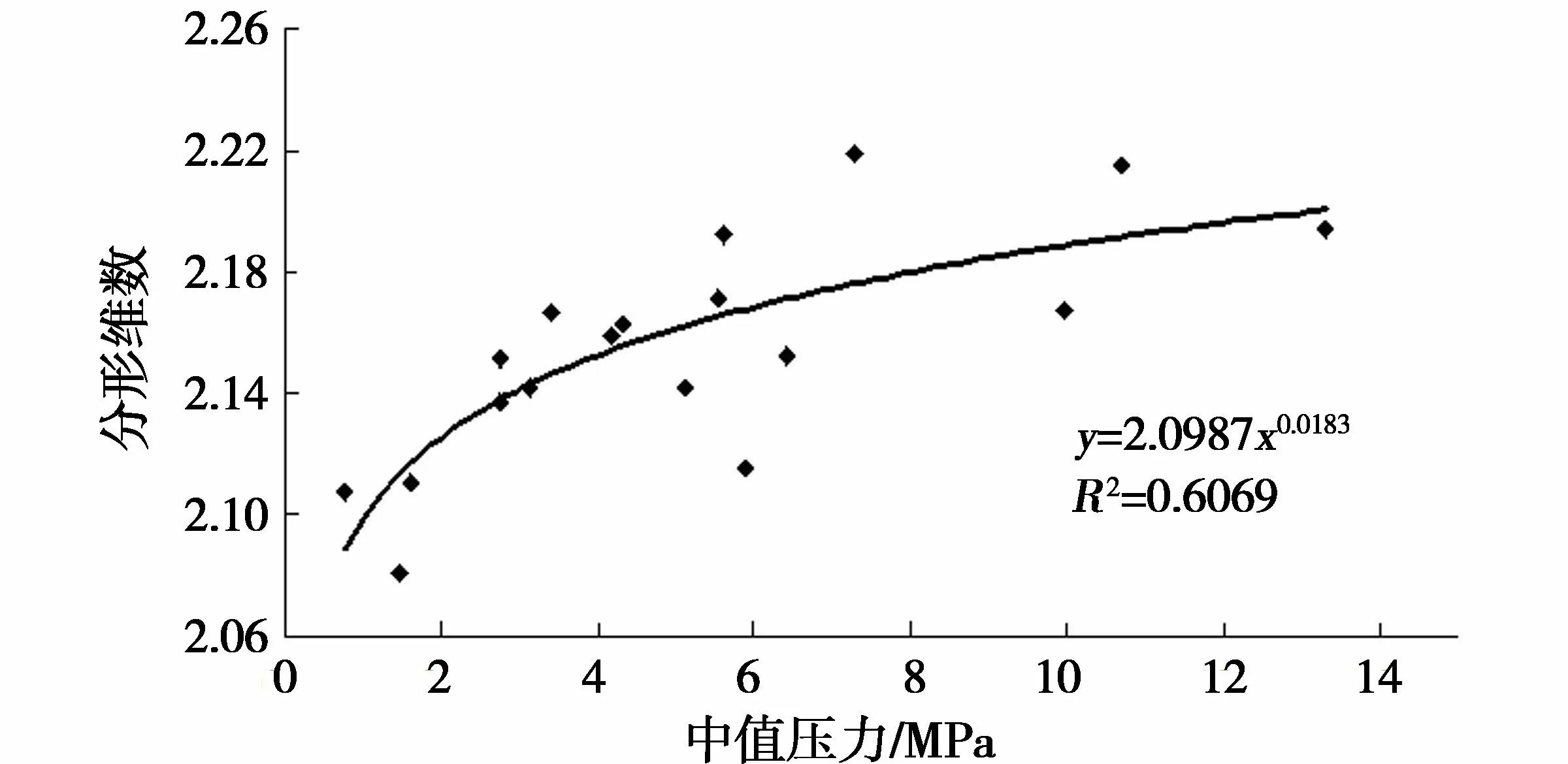
图4 中值压力与分形维数的关系

(2)中值半径和最大连通孔喉半径。中值半径指非润湿相饱和度为50%时所对应的孔喉半径，它是孔隙喉道大小分布趋势的量度。排驱压力所对应的孔喉半径即为最大连通孔喉半径。整体上二者与分形维数呈负相关(图5、图6)，分形维数越小，最大连通孔喉半径和中值半径越大，岩石中大孔隙越多，流体越容易流动。结合岩心资料和铸体薄片分析，大孔隙内溶蚀作用明显，岩石储集性能好。

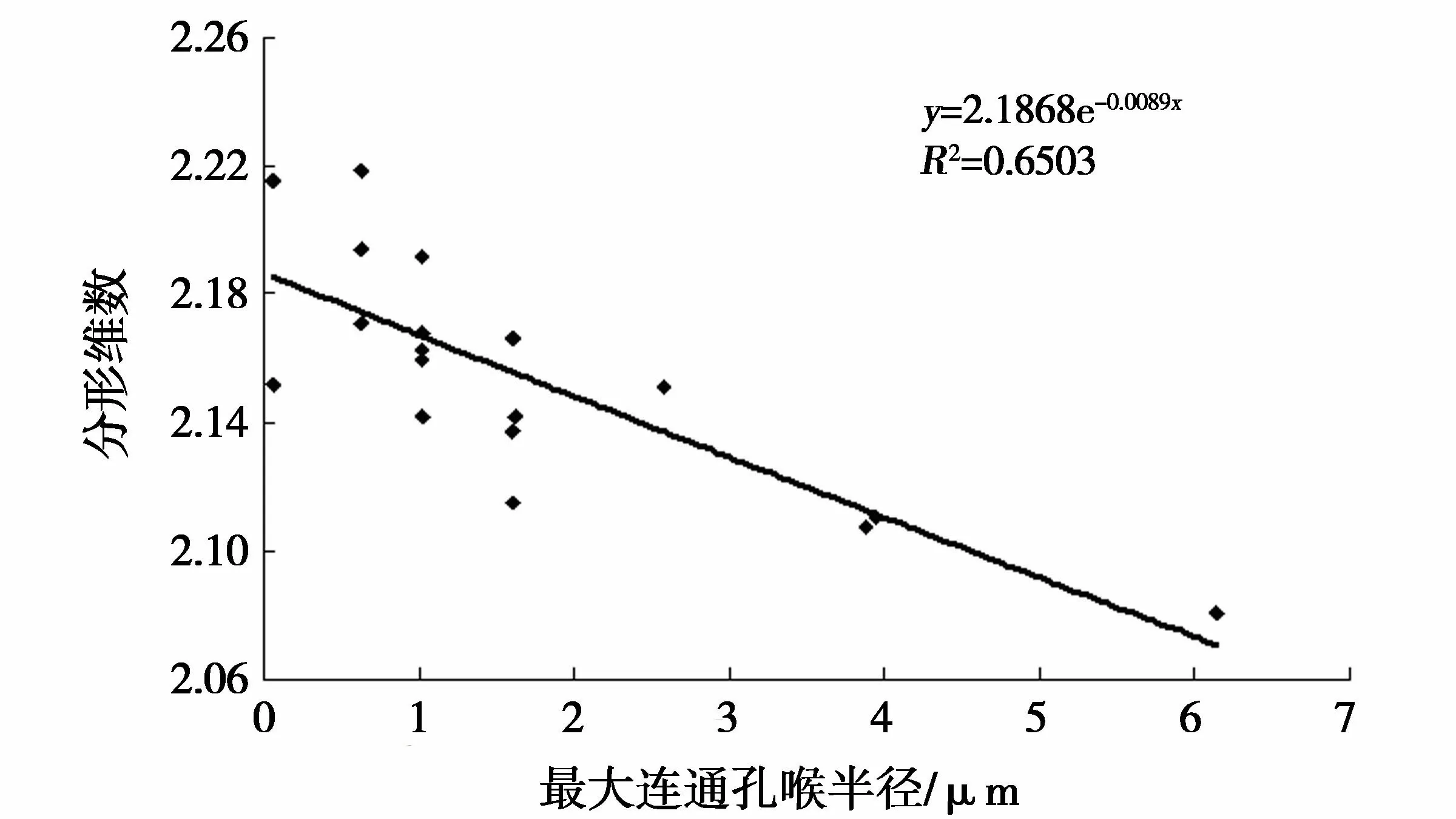
图5 最大连通孔喉半径与分形维数的关系

图6 中值半径与分形维数的关系

4.2.2 孔喉分布与分形维数的关系

变异系数和均值系数一定程度上都能反映孔喉分布，所不同的是，变异系数是反映孔喉大小相对均匀程度的参数，均值系数则反映孔隙介质中每个喉道半径与最大喉道的偏离程度。变异系数越小，均值系数越大，孔隙表面越光滑，孔喉分布越均匀，均质性越强。由图7、图8可以看到，均值系数与分形维数呈良好的正相关性，分形维数大，均值系数大，说明分形维数可用于定量表征储层微观孔喉分布非均质性。变异系数与分形维数整体上呈负相关，但相关性较差，分析认为这与所选样品的数量或参数自身有关。因为变异系数是根据岩样孔喉部分特征点数据计算出的结果，并不能反映整体孔喉分布的结构特征，不同孔隙结构的变异系数可能相同，而分形维数与孔喉分布的非均质性有关，因而更能合理地定量描述微观孔喉分布的结构特征。

4.2.3 孔喉连通性与分形维数的关系

孔隙系统的渗流能力除与孔喉大小及分布有关外，还受孔喉连通性及孔喉配置关系的控制，孔喉比即是反映这种特征的重要参数之一。研究区分形维数与孔喉比呈明显的正相关性(图9)，分形维数愈大，孔喉比值愈高，孔隙连通性愈差，岩石的渗滤能力愈低，非润湿相流体在孔隙空间系统内残留的愈多，油田采收率愈低。

图7 变异系数与分形维数的关系

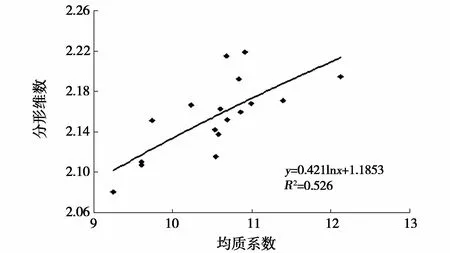
图8 均质系数与分形维数的关系

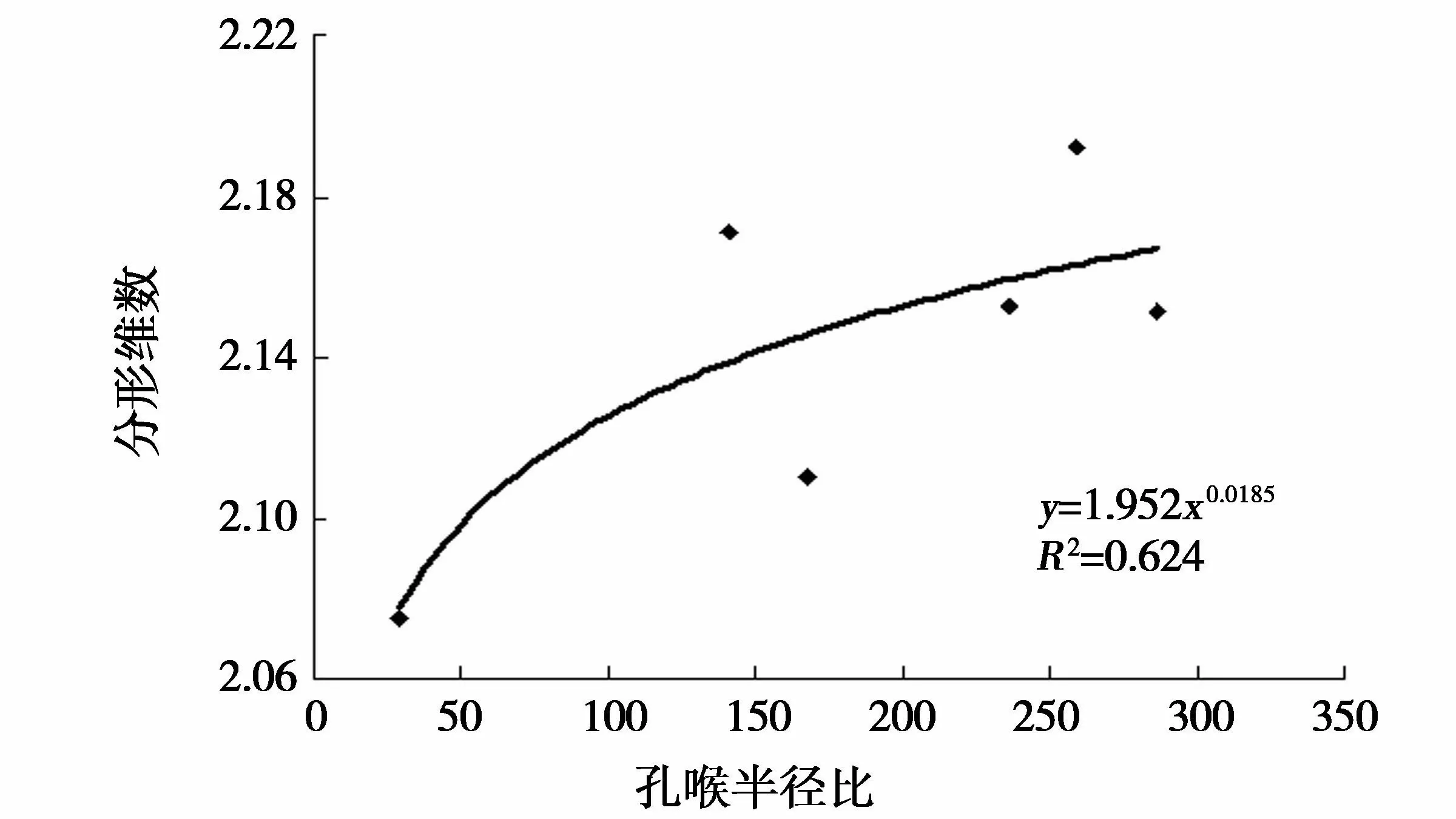
图9 孔喉半径比与分形维数的关系

5 结论

(1)致密砂岩储层孔隙结构具有统计自相似和分形特征，其分形维数可根据分形几何理论，结合压汞资料中的毛管压力曲线求取。

(2)致密储层孔隙结构的分形维数为2.0～2.3，且只有当孔隙半径大于趋势线拐点所对应的孔隙半径时，孔隙结构才具有分形特征。

(3)孔隙结构的分形维数与储层物性及孔隙结构各类参数的相关性良好，分形维数越小，孔隙喉道表面越光滑，孔隙分布越均匀，连通程度越高，储层微观非均质性越弱，储集性能和渗流能力越强。孔隙结构分形维数可综合反映孔隙空间复杂程度和非均质性的地质意义，使微观孔隙结构研究从传统的定性描述向定量化发展。

[1] 杜伯仁.分形理论及在地学中的应用简介[J].地质科技情报，1991,10(1)：69-72.

[2] 高永璋，张寿庭，孙社良，等.新疆塔什库尔干-莎车一带断裂体系的分形特征及找矿预测[J].现代地质，2011,25(1)：101-107.

[3] Torcotte D L.A fractal approach to the relationship between one grade and tonnage[J].Economic Geology，1996,81：1528-1532.

[4] 张志强，郑卫军.低渗透油气资源勘探开发技术进展[J].地球科学进展，2009,24(8)：854-864.

[5] 师调调，孙卫，何生平，等.低渗透储层微观孔隙结构与可动流体饱和度关系研究[J].地质科技情报，2012,31(4)：81-85.

[6] 姜洪福，陈发景，张云春，等.松辽盆地三肇地区扶、杨油层储集层孔隙结构及评价[J].现代地质，2006,20(3)：465-472.

[7] 何文祥，杨乐，马超亚，等.特低渗透储层微观孔隙结构参数对渗流行为的影响[J].天然气地球科学，2011，22(3)：477-481.

[8] Kalz A J, Thompson A H. Fractal sandstone pore: [J].地球科学进展，2009,24(8)：854-864.

[9] 李留仁，赵艳艳，李忠兴，等.多孔介质孔隙结构分形特征及分形系数的意义[J].石油大学学报(自然科学版)，2004，28(3)：105-114.

[10] 马立民，林承焰.基于微观孔隙结构分形特征的定量储层分类与评价[J].石油天然气学报，2012，34(5)：15-19.

[11] 张婷，徐守余，杨柯.储层微观孔隙结构分形维数应用[J].大庆石油学院学报，2010，34(3)：44-47.

[12] 张宸恺，沈金松，樊震.应用分形理论研究鄂尔多斯MHM油田低孔渗储层孔隙结构[J].石油与天然气地质，2007，28(1)：110-115.

[13] 李艳松，张捍民，孟凡刚，等.分形理论在多孔介质渗透性能的研究[J].过滤与分离，2006，16(1)：14-17.

[14] 杨庆红，谭吕，蔡建超，等.储层微观非均质性定量表征的分形模型[J].地球物理学进展，2012，27(2)：603-609.

[15] 李留仁，袁士义，胡永乐.分形多孔介质渗透率与孔隙度理论关系模型[J].西安石油大学学报(自然科学版)，2010，25(3)：49-52.

[16] 周江羽，袁艳斌，李星.地学分形研究中值得注意的几个问题[J].地质科技情报，1999，18(2)：93-96.

[17] 贺伟，钟孚勋，贺承祖，等.储层岩石孔隙的分形结构研究和应用[J].天然气工业，2000，20(2)：67-70.

[18] 陈程，孙义梅.砂岩孔隙结构分维及其应用[J].沉积学报，1996，14(4)：108-113.

[19] 马新仿，张士诚，郎兆新.孔隙结构特征参数的分形表征[J].油气地质与采收率，2005，12(6)：34-36.

[20] 岳新建，刘顺生.克拉玛依油田三叠系砾岩储层孔隙结构分形特征[J].新疆石油地质，1996，17(4)：391-395.

[21] 徐守余，王淑萍.砂岩储层微观孔隙分形特征研究[J].天然气地球科学，2013，24(5)：886-893.

[22] 李中锋，何顺利，杨文新，等.微观物理模拟水驱油实验及残余油分布分形特征研究[J].中国石油大学学报(自然科学版)，2006，30(3)：67-76.

[23] 陈亮，谭凯旋，刘江. 新疆某砂岩铀矿含矿层孔隙结构的分形特征[J].中山大学学报(自然科学版)，2012，51(6)：139-144.

编辑：李金华

1673-8217(2015)06-0103-05

2015-06-17

杨海,1988年生，2011年毕业于西北大学，油气田开发工程专业在读硕士研究生，现主要从事油气田开发地质与储层研究工作。

国家科技重大专项“大型油气田及煤层气开发”(2011ZX05044)。

TE319

A