三线摆测量转动惯量方法的改进及不确定度分析

娄航宇,王 威,孙维民

(沈阳工业大学,辽宁沈阳 110870)

三线摆测量转动惯量方法的改进及不确定度分析

娄航宇,王 威∗,孙维民

(沈阳工业大学,辽宁沈阳 110870)

不确定度是评估测量结果准确性的重要参数。文中在测量刚体转动惯量的新方法“相对测量法”的基础上,给出其不确定度计算公式。新方法通过数学变换,省去了对上悬盘r及上下悬盘距离H的测量,可有效地减小误差。结果表明,公式改进后的计算结果较传统法相对误差降低0.84%,并且随着转角θ的增加,相对误差也随之增大,实验结果与理论分析一致。

三线摆;转动惯量;相对测量法;不确定度

转动惯量是表征刚体转动惯性大小的物理量,其大小与刚体的总质量,质量分布和转轴的位置均有关。目前刚体转动惯量的测量方法众多,如拉伸法、扭摆法、动力学法以及三线摆法[1]。其中三线摆法具有仪器简单、操作方便、精度较高等优点,因此在实践中得到广泛应用[2]。但由于数据处理不当或在实验时调试仪器方法欠缺等因素,经常会出现实验结果与理论数值误差较大的现象。因此引入不确定度可以对比不同的测量结果,评估测量结果的准确性[3-4]。文献[5]中提到了测量转动惯量的新方法,即采用相对测量法,得到精度较高的测量结果,但未对新公式进行不确定度的计算和分析。因而,本文基于改进后的转动惯量计算公式,推导出三线摆测量转动惯量的不确定度,并与传统法计算的误差进行了比较。

1 刚体转动惯量测量公式推导与改进

1.1 刚体转动惯量测量公式的推导

设上下悬盘点间距分别为r,R;上下悬盘间距离为H,下悬盘质量为 m0。在转角θ为8°左右时,下悬盘的运动可近似为简谐运动。当下悬盘离开平衡位置距离最远时,下悬盘质心上升h。若忽略阻力不计,则根据机械能守恒定律得:

即

由(2)(3)可得

(T0下盘空载时的周期)。若在下盘放置质量为 m1的物体,那么

根据(4)(5)可得

1.2 刚体转动惯量测量公式的改进

若采用上述方法测量,则需要测量m0,m1,r, R,H,T0,T17个物理量,在测量中造成偶然误差会很多。故利用数学方法将公式进行变换处理,在减少测量量的同时,也降低了产生偶然误差的机会,进而提高了测量结果的精度。

将(4)(5)式相除得:

2 不确定度分析及公式

分别对上下悬盘点间距r,R;上下悬盘的距离H;待测圆柱直径 D柱;下悬盘质量 m0及圆柱质量 m1进行测量。用光电门与毫秒计时器分别记录下悬盘空载和载物状态下周期 T0,T1。在转角θ为8°时测量3次,每次测量40组数据取平均值,记录数据如表1和表2所示。

根据不确定度的计算公式分别对 m0,m1,r, R,H,T0,T1等物理量进行A类、B类及合成不确定度计算,结果如表3所示。

表1 质量及周期的测定

表2 上下盘几何参数及圆柱体直径的测量结果

表3 各物理量的不确定度计算结果

通过推导得出传统法不确定度的计算公式为:

相对测量法不确定度的计算公式为:

3 实验结果及讨论

3.1 传统法数据处理结果

(1)圆柱转动惯量的理论值:

(2)将测量结果代入公式求得圆柱的转动惯量: =1.327×10-5kg·m2

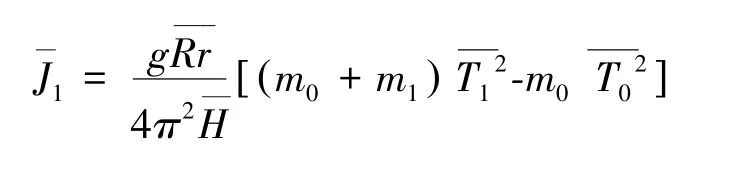
(3)不确定度计算:

将表2、3中的数据代入公式⑼中得到:

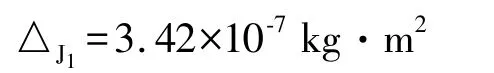
(4)测量值结果为: ×100%= 2.2%

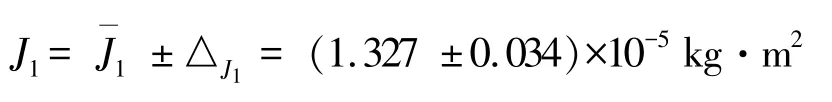
3.2 改进法数据处理结果

(1)将测量结果代入公式求得圆柱的转动惯量:

(2)不确定度计算:

将表2、3中的数据代入公式⑽中得到:

(3)测量值结果为:

经上文测量计算结果比较可知,改进后的公式相对误差较传统公式相对误差降低了0.84%,可见公式改进后的“相对测量法”相比于“传统测量法”测量精度提高很多。

3.3 扭转角度对测量结果的影响

在相对测量法中,测量量有 m0,m1,R,T0, T1等5个物理量,而周期 T0,T1的不确定度是决定总不确定度的重要因素,转角θ决定周期的大小[6-7]。因此本文研究了不同转角下对应的相对误差。所得结果见表4,转角θ与相对误差的关系曲线如图1所示。

表4 不同转角θ下对应的相对误差

图1 转动惯量的相对误差与转角θ关系

图2

当转角θ为10°时,相对误差为3.62%。故表4结果与文献[8-10]中所述一致,当转角θ不超过8°时不会对实验结果造成较大影响。

4 结 论

三线摆测量转动惯量是一种常用的方法。本文中测量刚体转动惯量不确定度的新公式具有表达简洁、计算精度较高等优点,基本可取代传统的计算公式。新的实验数据处理方法采用了新的计算公式,以下悬盘的转动惯量为标准进行度量,可以显著减小相对误差。在实际操作中实验误差是在所难免的,如仪器转动会受到空气阻力所带来的影响,扭转的最大角位移及操作误差都会带来实验误差[9-10]。故在实验中应采取适当的措施进行改进,最大限度的减小实验误差。

[1] 孙维民,宋大毅,姜源,等.物理实验教程[M].北京:科学出版社,2011:82-84.

[2] 夏雪琴.“比较测量法”在三线摆实验中的应用[J].大学物理实验,2011,24(5):47-50.

[3] 强蕊.三线摆法测刚体转动惯量的不确定度分析[J].西安科技大学学报,2011,31(5):631-635.

[4] 毛爱华.三线摆测量物体转动惯量的不确定度计算[J].阴山学刊,2005,19(2):23-24.

[5] 张勇.三线摆测量刚体转动惯量实验数据处理的新方法[J].内肛科技,2011(8):95-99.

[6] 万志龙.三线摆测量刚体转动惯量实验的不确定度分析[J].长春师范学院学报,2010,29(5):28-31.

[7] 药树栋.三线摆测刚体转动惯量的误差分析[J].内蒙古电大学刊,2006(5):105-106.

[8] 毕江林,沈一铭,王威.三线摆测量刚体转动惯量及其误差分析[J].科教文汇,2013(256):86-87.

[9] 赵敏福.三线摆测量转动惯量的误差分析[J].科技信息,2009(2):408-409.

[10]庞通,黄艺荣,等.三线摆实验中摆角偏大产生误差及修正方法[J].大学物理实验,2015(1):33-35.

Im provement and Uncertainty Analysis of Tri-linear Pendulum M oment of Inertia of Rigid M ethods

LOU Hang-yu,WANGWei,SUNWei-min
(Shenyang University of Technology,Liaoning Shenyang 110870)

Uncertainty is an important parameter to assess the accuracy of themeasurement results.On the basis of the article"relativemeasurement"of the new method ofmeasuring rigid bodymoment of inertia,the formula of the uncertainty has been given.The new method through mathematical transform,eliminating themeasurement of suspended plate r and the upper and lower hanging plate distance H,can significantly reduce the error.The results show that the relative error calculated by the improved formula is reduced by 0.84%compared with the traditionalmethod.Moreover,with the increase of the angle,the relative error increases,the experimental results are consistentwith the theoretical analysis.

tri-linear pendulum;moment of inertia;relativemeasuringmethod;uncertainty

O 4-34

A

10.14139/j.cnki.cn22-1228.2015.006.030

1007-2934(2015)06-0102-04

2015-07-13

辽宁省普通高等学校本科实验教学示范中心建设项目(S201144);沈阳工业大学教育教学改革重点项目(2011-35)

∗通讯联系人