耦合映像格子模型时空混沌的控制
2015-07-01谷开慧孙晓冰刑淑芝
刘 璐,谷开慧,孙晓冰,刑淑芝,孟 瑜
(长春理工大学,吉林长春 130000)
耦合映像格子模型时空混沌的控制
刘 璐,谷开慧,孙晓冰,刑淑芝,孟 瑜
(长春理工大学,吉林长春 130000)
采用非线性反馈方法研究耦合电光双稳映像格子混沌系统的控制。画出空间振幅变化图。数值模拟的结构表明:在一定的相空间压缩参数区域内,控制时空混沌到均匀稳定状态时,控制结果与控制参数之间存在关系。同时利用计算机模拟了相应参数下的时序图,格点处于稳定状态,从而证明常数偏移法的有效性。
电光双稳系统;时空混沌;控制
自Ott等[1]提出混沌控制理论(OGY)以来,混沌控制及其应用引起人们广泛关注[2-6]。近年来,研究人员已提出多种混沌控制理论方法,如连续变量反馈控制法、自适应控制法及参数微扰法[7-8]等。时间混沌的研究发展的越来越快,混沌控制的方法也越来越多,但是对于时空混沌来说研究的相对较少,而且时空混沌比时间混沌更复杂,保密性更高,更适于保密通信。文章中采用常数偏移法和非线性反馈的方法对耦合映像电光双稳系统映像格子进行研究,取不同的参数值,数值模拟该模型的时序图,从而证明了该方法有效。
1 电光双稳系统混沌模型
图1为电光双稳系统装置图。

图1 电光双稳系统装置图
文章中以耦合电光双稳映像格子模型为研究的对象,研究混沌的同步问题,基于Lyapunov稳定性理论,通过选择适当的驱动函数,实现时空混沌的完全同步,为了验证此种方法的有效性,采用了数值仿真的方法对其系统进行研究。
采用的动力学方程为:

其中f(xn(i))表示局域动力学函数,取电光双稳系统模型,n表示离散的时间变量,i表示映象格子的空间坐标,i=1,2Λ,L,L是系统的尺寸,格点间的耦合强度用ε表示,xn为系统的状态变量。(1)式为一维耦合电光双稳映象格子模型,取随机的初始条件,边界条件取xn(0)=xn(L+1) =0。
2 非线性反馈的方法实现时空混沌的控制
一维耦合电光双稳映像格子模型,其动力学方程(1)在计算机数值模拟中,当I=6.1、ε=0.1、K=0.8时,系统为完全发展湍流模式。对于这个模型,采用下面的非线性局部反馈控制的方法,即
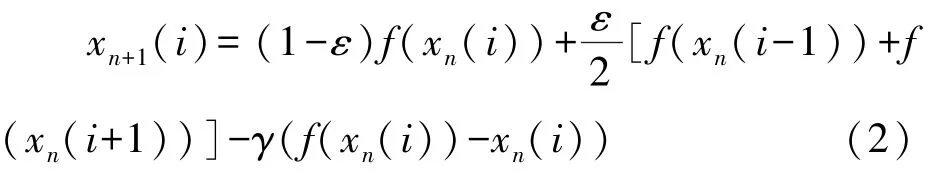
γ是反馈系数。
2.1 空间振幅变化图
通过选取不同的反馈系数γ,方程处于不同的时空模式,取x(1)=x(100)=0如图所示,反馈系数不同时,系统的空间振幅变化图也不同,下面分别讨论γ=0.1、0.3、0.5、0.85、0.9时受控系统的时空行为,见图2~图6。
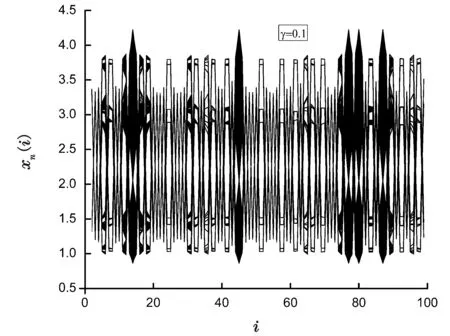
图2 反馈系数为0.1时,空间振幅变化图

图3 反馈系数为0.3时,空间振幅变化图

图4 反馈系数为0.5时,空间振幅变化图

图5 反馈系数为0.85时,空间振幅变化图

图6 反馈系数为0.9时,空间振幅变化图
由图2可以看出,当反馈系数取0.1时,电光双稳时空模型是图案选择模式,具有团选择模式的特点,部分格点处于周期态,大多数格点处于混沌态,随着反馈系数的增加,系统的模式区域稳定,呈冻结化随机图案模式,格点均处于二周期态,进一步增大反馈系数,此时反馈系数为0.5,除了L=1和L=100附近的几个格点以外,其他格点均处于不稳定不定点的位置,并且保持稳定,不随时间变化,但是继续增大反馈系数时,边缘区域处于非不稳定平衡点位置的格点增多,稳定的范围变小,处于单周期态的格点变少,L=1和L= 100附近的不稳定格点的数目增加,直至所有格点都不处于周期态而是处于2点周期,每个格点的周期态都不相同。
2.2 时序图
为了验证上述方法的有效性,取反馈系数0.5,第50个格点的时间序列和未对系统施加控制时的时间序列。当系统运行到N=10 000时,开始采用上面提出的方法对系统的每个格点进行控制,从图7、图8中可以看出,当系统反映9 000多步迭代时,第50个格点处于四周期态,并且一直处于四周期稳定态,若在迭代到10 000步时,对系统施加有效的控制,此格点瞬间被控制到单周期不稳定不动点,因此,这种控制的方法具有一定的高效性和准确性。

图7 第50个格点在10 000步迭代受控时的时序图

图8 第50个格点的时序图
当γ=0.1时,系统的空间振幅变化图是图案选择模式,某些特定的格点处于倍周期状态;当γ =0.3时,此时,处于冻结化随机图案模式,每个格点均处于倍周期状态,随着反馈系数的增加,此种方法可以将大多数的个点控制在不稳定平衡点的位置,反馈系数继续增加,边缘区域处于非不稳定平衡点位置的格点增多,稳定的范围变小,因此,可以选择不同的反馈系数来控制系统的格点的状态。
3 结 论
根据系数对耦合映像格子模型时空混沌的影响提出非线性反馈的方法对其进行控制,同时画出了空间振幅变化图和响应的时序图,数值模拟的结果表明了该方法的有效性,由于时空混沌信号的复杂性较高,所以具有更广泛的应用前景。
[1] Ott E,Grebogi C,Yorker JA.Controlling Chaos[J]. Phys.Rev.Lett.1190,64(11):1196-1199.
[2] L.M.Peeora.Chaosineorn Nunieations[J].Proe. SPIE.1993:2038-2044P
[3] H.Dedieu,M.P.Kennedy,M.Hasler.Chaos Shift Keying:Modulation and Demodulation ofa Chaotic Carrier Using Self-synchronizing Chua’s Circuits[J].IEEE Transaction on Circuits and SystemsⅡ,1993,40(2): 634-642.
[4] M.Sushchik,L.S.Tsimring,A.R.Volkovskii.Performance Analysis of Correlation-based Communication Schemes Utilizing Chaos[J].IEEE Transaction on Circuits and Systems I,2001,48(12):1684-1691.
[5] A.Abel,W.Schwatz,M.Gotz.Noise Performance of Chaotic Communication Systems[J].IEEE Transaction on Circuits and Systems I,2000,47(12):1726-1732.
[6] M.P.Kennedy,G.Kolumban,G.Kis etal.Performance Evaluation of FM-DCSK Modulation in Multipath Environments[J].IEEE Transaction on Circuits and Systems I,2001,48(12):1702-1717.
[7] T Yang.Recovery of Digital Signals From Chaoticswitching[J].Circuit Theory Appl.1995,23(6): 611-615
[8] Kuang-You Lian,Chian-Song Chiu,Tung-Sheng Chiang,Peter Liu.LMI-based Fuzzy Chaotic Synchronization and Communication[J].IEEE Transaction on Fuzzy Systems,2001,9(4):539-553.
Controlling Spatiotem poral Chaos in Coupled M ap Lattice System
LIU Lu,GU Kai-hui,SUN Xiao-bing,XING Shu-zhi,MENG Yu
(Changchun University of Science and Technology,Jilin Changchun 130000)
Spatiotemporalmodes of a coupledmap lattice chaotic electrical-optical bistable system were studied by means of the nonlinear feedback method and constant diviation method.We have draw space-amplitude plot.Numerical simulation results show that there is a definite functional relationship between the control results and control parameters in a certain region of compressed phase space,when we control the spatiotemporal chaos to homogeneous stable state。The state was very steading by sequence diagram.We would prove that the constant diviation method was effective.
electrical-optical bistable;spatiotemporal chaos;control
O 4-34
A
10.14139/j.cnki.cn22-1228.2015.006.004
1007-2934(2015)06-0011-03
2015-08-06
