毕竟正则半群上的模糊群同余

杨 燕，李 超，乔希民，刘晓民

(商洛学院数学与计算机应用学院,陕西商洛 726000)

毕竟正则半群上的模糊群同余

杨 燕，李 超，乔希民，刘晓民

(商洛学院数学与计算机应用学院,陕西商洛 726000)

毕竟正则半群是一类重要的广义正则半群,利用半群模糊同余的概念,获得了毕竟正则半群上群同余的一些新刻画,并给出了毕竟纯整半群上一个模糊同余为模糊群同余的充要条件.

毕竟正则半群;模糊同余;模糊群同余;毕竟纯整半群

0 引言

半群同余理论的研究一直是半群研究的热点问题,近些年来,半群研究不但朝着广义正则半群发展,而且各类半群上模糊同余的研究也引起了许多国内外学者的关注.自Samhan[1]定义和研究了半群的模糊同余关系之后,Al-Thukair[2]引入了逆半群上模糊核、模糊迹的概念，并用模糊核-迹的方法给出了逆半群上模糊同余的刻画.谢祥云[3]研究了半群上模糊同余的扩张，给出了其同态性质.李勇华等[4]引入了半群的模糊半正规子半群的概念，并利用它研究了半群上的模糊群同余；证明了正则半群上的每个模糊同余是由它的模糊三元组惟一确定的[5].李春华等[6-8]对几类广义正则半群，如适当半群、型A半群、富足半群上的模糊好同余作了研究,同时也研究了Clifford半群[9]和严格π-正则半群[10]上模糊同余的性质和特征,得到了很好的结论.

本文利用半群模糊同余的概念和元素的“弱逆”,研究毕竟正则半群上的群同余，给出模糊群同余的新刻画,并讨论毕竟纯整半群上一个模糊同余为模糊群同余的几个充要条件.文中未给出的定义和记号参见文献[11-13].

1 预备知识

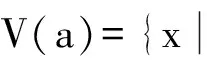
定义1[13]令μ,v为半群S上的两个模糊关系,对∀x,y∈S,定义

μ⊆v⟺∀x,y∈S,μ(x,y)≤v(x,y);

μ∘v(a,b)=∨x∈S{μ(a,x)∧v(x,b)}.

定义2[13]称半群S上的模糊关系μ为S上的模糊等价关系,如果对任意的a,b∈S,满足：μ(a,a)=1,μ(a,b)=μ(b,a),μ∘μ⊆μ.

定义3[12]称半群S上的模糊关系μ在S上关于乘法是相容的,如果对任意的a,b,x∈S,满足：μ(ax,bx)≥μ(a,b),μ(xa,xb)≥μ(a,b).

若半群S上的模糊等价关系μ关于乘法是相容的,则称μ是S上的模糊同余.对a∈S,用μa表示S中所有与a具有模糊等价关系μ的模糊子集,即μa(x)=μ(a,x),∀x∈S.用Cρ表示半群S上的二元关系ρ的特征函数,即对∀a,b∈S，有

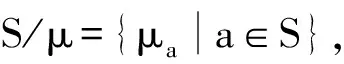
引理1[13]设μ为半群S上的模糊同余,a,b∈S,则下列结论成立：

(1)μa=μb⟺μ(a,b)=1;

2 主要结果

定理1的证明与文献[10]中定理2的证明类似,这里不再赘述,但需注意的是证明时要用(an)′∈W(an)替换原来证明中出现的(an)′∈V(an),因为定理1中使用的是满的、弱自共轭的子半群H.

推论1 设μ为毕竟纯整半群S上的模糊同余,则

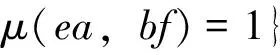
为S上的群同余.

证明 显然,E(S)是S的子半群,且是满的.又对∀e,f∈E(S),∀a∈S,∀(an)′∈W(an),由于an-1(an)′a,e∈E(S)且E(S)是子半群,所以

即有aean-1(an)′∈E(S).同理可得an-1(an)′fa∈E(S),因此E(S)是弱自共轭的,由定理1知,结论成立. 】

下面利用模糊同余给出μH的一些等价刻画.

定理2 设μ为毕竟正则半群S上的模糊同余,H是S满的、弱自共轭的子半群,μH的定义如定理1所示,对∀a,b∈S,设n,m分别为a,b的正则指数,则下列结论等价:

(1)aμHb;

(2)∃x,y∈H，使得μ(ax,yb)=1;

(3)对∀(bm)′∈W(bm),∃x,y∈H，使得μ(axbm-1(bm)′,y)=1;

(4)对∀(bm)′∈W(bm),∃x,y∈H，使得μ(bm-1(bm)′xa,y)=1;

(5)∃x1,x2,y1,y2∈H，使得μ(x1ax2,y1by2)=1;

(6)对∀(an)′∈W(an),∃x,y∈H，使得μ(bxan-1(an)′,y)=1;

(7)对∀(an)′∈W(an),∃x,y∈H，使得μ(an-1(an)′xb,y)=1.

证明 (1)⟹(2).设a,b∈S,aμHb,则存在x,y∈H使得μ(xa,by)=1.由引理1中的(1)可知μxa=μby,给此等式左乘μan(an)′,右乘μbm-1(bm)′b,其中n,m分别为a,b的正则指数,(an)′∈W(an),(bm)′∈W(bm),则有

于是μ(aan-1(an)′xabm-1(bm)′b,an(an)′bybm-1(bm)′b)=1.令

因为H为S的满的、弱自共轭的子半群,所以an-1(an)′xa,bybm-1(bm)′∈H,bm-1(bm)′b,an(an)′∈E(S)⊆H.故x1,y1∈H,从而μ(ax1,y1b)=1.

(2)⟹(1).设存在x,y∈H,使得μ(ax,yb)=1,则由引理1中的(1)可知μax=μyb.给此等式左乘μbm(bm)′,右乘μan-1(an)′a,其中n,m分别为a,b的正则指数,(an)′∈W(an),(bm)′∈W(bm),则有

于是μ(bm(bm)′axan-1(an)′a,bbm-1(bm)′yban-1(an)′a)=1.令

因为H为S的满的、弱自共轭的子半群,所以x2,y2∈H,且满足μ(x2a,by2)=1.进而aμHb.

(2)⟹(3).设存在x,y∈H,使得μ(ax,yb)=1,则由引理1中的(1)可知μax=μyb.对任意的(bm)′∈W(bm),给此等式两端同时右乘μbm-1(bm)′,得

令y1=ybbm-1(bm)′,则y1∈H，进而μaxbm-1(bm)′=μy1.故存在x,y1∈H,使得μ(axbm-1(bm)′,y1)=1.

(3)⟹(2).设对任意的(bm)′∈W(bm),存在x,y∈H,使得μ(axbm-1(bm)′,y)=1.则μaxbm-1(bm)′=μy,右乘μb,得μaxbm-1(bm)′·b=μyb.令xbm-1(bm)′·b=x1,由于x∈H,bm-1(bm)′b∈E(S)⊆H,所以x1∈H.故存在x1,y∈H,使得μax1=μyb,即μ(ax1,yb)=1.

类似可证(1)与(4)等价,于是(1)～(4)各款等价.

(2)⟹(5).设存在x,y∈H,使得μ(ax,yb)=1,则μax=μyb.给等式两端左乘μx,右乘μy,得μx*μax*μy=μx*μyb*μy,即μxaxy=μxyby.因为x,y∈H,xy=x1=y1∈H,所以存在x,x1,y,y1∈H,使得μxax1=μy1by,即μ(xax1,y1by)=1.

(5)⟹(2).设存在x1,x2,y1,y2∈H,使得μ(x1ax2,y1by2)=1，则μx1ax2=μy1by2.给该等式两端同时左乘μan(an)′,右乘μbm-1(bm)′b,得

即

令

因为H是S的满的、弱自共轭的子半群,所以an-1(an)′x1a∈H,bm-1(bm)′b∈E(S)⊆H,故x∈H.又an(an)′∈E(S)⊆H,by2bm-1(bm)′∈H,故y∈H.因此存在x,y∈H,使得μax=μyb,即μ(ax,yb)=1.

(1)⟹(7).设a,b∈S,aμHb.由定理1知μH是对称的,所以bμHa.根据定理1中μH的定义可知,存在x,y∈H,使得μ(xb,ay)=1,于是μxb=μay.对∀(an)′∈W(an),等式两边同时左乘μan-1(an)′,得

令an-1(an)′ay=y1,则y1∈H.故存在x,y1∈H,使得μan-1(an)′xb=μy1,即μ(an-1(an)′xb,y1)=1.

(7)⟹(1).设对任意的(an)′∈W(an),存在x,y∈H,使得μ(an-1(an)′xb,y)=1.于是有μan-1(an)′xb=μy,给等式两边同时左乘μa得μaan-1(an)′xb=μay,其中x1=aan-1(an)′x∈H.故存在x1,y∈H,使得μx1b=μay,进而(b,a)∈μH.由定理1知μH是对称的,所以aμHb.

同理可证(2)与(6)等价.

综上,结论(1)～(7)等价. 】

定理3 设μ为毕竟正则半群S上的模糊同余,H是S的满的、弱自共轭的子半群,则有

(1)CμH为S上的模糊群同余；

(2)若CμH⊆μ，则μ为S上的模糊群同余.

证明 (1) 由于ρ为S上的同余等价于ρ的特征函数Cρ为S上的模糊同余,由定理1知μH为S上的群同余,所以CμH为S上的模糊群同余.

(2)由(1)可知S/CμH是群,所以对任意的e,f∈E(S),有(CμH)e=(CμH)f,根据引理1中的(1)可知CμH(e,f)=1.另一方面，对任意a∈S,e∈E(S),由CμH为模糊群同余,有

所以CμH(ae,a)=1,CμH(ea,a)=1.根据定义1知CμH⊆μ当且仅当∀x,y∈S,CμH(x,y)≤μ(x,y).因为CμH⊆μ,所以对任意的e,f∈E(S),a∈S,有μ(e,f)=1,μ(ae,a)=1,μ(ea,a)=1.根据引理1中的(1),μe=μf,μae=μa=μea,即μa*μe=μa=μe*μa.所以μe为S/μ的单位元.

对任意μa∈S/μ,设a′∈W(a),则aa′,a′a∈E(S),从而μa*μa′=μaa′=μe,μa′*μa=μa′a=μe.所以μa′是μa在S/μ中的逆.

综上所述,S/μ是群,即μ为S上的模糊群同余. 】

定理4 设μ为毕竟纯整半群S上的模糊同余，则下列结论等价:

(1)μ为S上的模糊群同余;

(2)CμE(S)⊆μ;

(3)μE(S)⊆μ-1.

证明 (1)⟹(2).设μ为S上的模糊群同余,分两种情形：(i) 若对任意a,b∈S,(a,b)∉μE(S),则CμE(S)(a,b)=0≤μ(a,b),根据定义1知CμE(S)⊆μ；(ii) 若对任意a,b∈S,(a,b)∈μE(S),则CμE(S)(a,b)=1且存在e,f∈E(S),使得μ(ea,bf)=1,即μea=μbf.又因为e,f均为幂等元,μ为S上的模糊群同余,所以μe=μf.于是μa=μea=μbf=μb,所以μ(a,b)=1,即CμE(S)⊆μ.综上,CμE(S)⊆μ .

(2)⟹(3).由定理3知μ为S上的模糊群同余.设a,b∈S,(a,b)∈μE(S),则由推论1知,存在e,f∈E(S),使得μ(ea,bf)=1,即μea=μbf.因为μ是S上的模糊群同余,所以μe=μf,从而μa=μe*μa=μea=μbf=μb*μf=μb,于是μ(a,b)=1.根据引理1中的(2),(a,b)∈μ-1,故μE(S)⊆μ-1.

(3)⟹(1).设μE(S)⊆μ-1，因为μE(S)为S上的群同余，所以对任意e,f∈E(S),eμE(S)=fμE(S),即(e,f)∈μE(S).由于μE(S)⊆μ-1,所以(e,f)∈μ-1，即μ(e,f)=1，根据引理1中的(1)可知μe=μf.对任意a∈S,e∈E(S)，因为μE(S)为群同余，所以(ae,a)∈μE(S),(a,ea)∈μE(S).又因为μE(S)⊆μ-1,所以(ae,a)∈μ-1,(a,ea)∈μ-1.根据引理1中的(2),μ(ae,a)=1,μ(a,ea)=1，从而μae=μa=μea,即μa*μe=μa=μe*μa,故μe为S/μ的单位元.又因为对任意a∈S,a′∈W(a),有μa*μa′=μaa′=μe=μa′a=μa′*μa,所以μa′是μa在S/μ中的逆.故S/μ是群,即μ为S上的模糊群同余. 】

[1] SAMHAN M.Fuzzy congruence on semigroups[J].InformSci,1993,74:165-175.

[2] AL-THUKAIR F A.Fuzzy congruence pairs of inverse semigroup[J].FuzzySetsandSystem,1993,56:117-122.

[3] XIE Xiang-yun.Fuzzy congruence extensions in semigroups[J].AdvancesinMathematics,2001,30(3):218-230.

[4] LI Yong-hua,XU Cheng-xian.Fuzzy group congruence on a semigroup[J].FuzzySystemsandMathematics,2002,16(4):57-62.

[5] 李勇华,徐成贤.正则半群的模糊同余三元组[J].西安交通大学学报,2002,36(4):418-421.

[6] 李春华.适当半群上的模糊好同余[J].南昌大学学报:理科版,2007,31(1):35-37.

[7] 李春华.型A-半群上的fuzzy好同余[J].山东大学学报:理学版,2008,43(2):40-43.

[8] 李春华,徐宝根.富足半群上的F-好同余[J].模糊系统与数学,2008,22(4):39-42.

[9] 李春华,徐宝根,黄华伟.关于Clifford半群上的fuzzy同余[J].模糊系统与数学,2011,25(3):37-40.

[10] 李春华,刘二根.严格π-正则半群上的fuzzy同余[J].中山大学学报:自然科学版,2011,50(5):11-14.

[11] HOIWE J M.FundamentalsofSemigroupTheory[M].Oxford:Clarendon Press,1995.

[12] 谢祥云,吴明芬.半群的模糊理论[M].北京：科学出版社,2005.

[13] JOHN N M,DAVENDER S M,NOBUAKI K.FuzzySemigroup[M].New York:Springer,2003.

(责任编辑 马宇鸿)

Fuzzy group congruences on eventually regular semigroups

YANG Yan,LI Chao,QIAO Xi-min,LIU Xiao-min

(School of Mathematics and Computer Application,Shangluo University,Shangluo 726000,Shaanxi，China)

Eventually regular semigroup is a class of important generalized regular semigroups.In this paper,some new characterizations of the group congruence on such semigroup by means of the notion of a fuzzy congruence on semigroups are obtained.Finally,sufficient and necessary conditions for a fuzzy congruence on an eventually orthodox semigroup to be a fuzzy group congruence are given.

eventually regular semigroup;fuzzy congruence;fuzzy group congruence;eventually orthodox semigroup

2013-11-30;修改稿收到日期:2014-06-21

商洛学院科研基金资助项目(13SKY014)

杨燕(1986—),女，甘肃舟曲人，讲师，硕士.主要研究方向为半群代数理论. E-mail:yanyangtianhao@163.com

O 152.7

A

1001-988Ⅹ(2015)04-0010-04