非均质地基的判定标准研究
2015-07-01孔滔
孔 滔
(新疆维吾尔自治区交通规划勘察设计研究院,新疆 乌鲁木齐 830006)
非均质地基的判定标准研究
孔 滔
(新疆维吾尔自治区交通规划勘察设计研究院,新疆 乌鲁木齐 830006)
非均质地基作为一种常见的地基,对于修建于其上的建筑物的安全稳定性具有较大的影响。对地基的非均质性目前尚无定量的判定方法。文章根据大量典型场地的剪切波速和岩体力学特性实测资料,提出了非均质地基的定量判定标准,并利用有限元软件ABAQUS建立了简化的二维模型,以地基的极限承载力作为衡量地基非均质性的指标,对模拟场地的极限承载力进行计算,同时根据计算结果对提出的判定标准进行了验证和调整。
非均质地基;定量;判定标准;ABAQUS
0 引言
地基的均质性广义上是指地基岩土的岩性、物理力学特性是否一致或接近,工程上的地基均质性可扩展到地基在外部荷载作用下是否会发生过大的沉降或出现较大沉降差。在非均质地基上修建建筑物时建筑物的安全性如何保证是一个很重要的问题,在设计中取多大的安全度也在很大程度上考验着设计者。鉴于此,判定场地是否为非均质地基就显得十分重要。但是,目前国内外关于非均质地基的确定方法研究还很少,实际中非均质地基的确定都是依靠工程技术人员的经验。
在国内对于岩石非均质地基的研究较少,现有的研究主要以定性评判为主,而以定量方法确定地基非均质性的研究几乎没有,如何解决定性评价已成为很多研究学者探讨的问题。《核电厂岩土工程勘察规范》意见征求稿[1]对于地基的均质性评判主要从地基岩性、岩性分布、岩石风化程度、地层产状、 岩土力学特性等方面考虑,当岩性相同或岩土物理力学特性一致或相近时,认为这种地基是均质的。但这种均质性地基在
现实中是很少的。工程中评价地基非均质性时应结合地基基础所受的荷载条件、基础的平面尺寸、基础埋置深度、地基承载力及变形等物理力学特性综合考虑。《高层建筑岩土工程勘察规程JGJ72-2004》[2]提出了3种非均质地基的判别标准,但是这些标准在实际应用中只实用于土层,因为岩层具有多变的岩性、差异的风化状态以及复杂的构造情况,所以《高层建筑岩土工程勘察规程JGJ72-2004》提出的分析方法并不适用于岩层。姬亦工[3]根据刚性路面力学模型,提出了层状非均质地基与多块板相互作用力的计算方法,提出了一种简化的粘弹性Kelvin地基,以及在这种粘弹性Kelvin地基上多块板的计算方法。屠晟[4]运用研究发展的安定性分析原理及计算方法,在考虑非均质地基的成层分布及粘结力沿深度的非均质变化模式下,确定了成层地基的安定载荷,然后根据数值计算结果对其系统进行了分析和讨论。彭彬[5]以广西右江白色水利枢纽工程修建在非均质地基上的消力池为典型例子,根据其基岩岩体软硬相间、物理力学性质差别大,存在高变模比、高承载力比、低抗冲性、风化深度空间变异性大的特殊地质条件,采用三维非线性有限元方法,对修建在非均质地基上的消力池的受力和变形特征进行了详尽分析,尽可能真实地模拟了消力池地基的岩层分布、节理及材料差异。M.M.格里申[6]将均质地基上坝的强度和抗剪设计理论引申到非均质地基中,考虑了坝底直接置于不同刚度的岩体或破裂构造区时坝的设计问题。唐良琴等[7]在大量实验研究以及总结前人研究成果的基础上,全面分析了物质组成、结构特征等因素对软弱夹层地基抗剪强度的影响。刘彬等[8]研究了软硬相间层状复杂的河湖相沉积岩的综合变形模量,包含了砾岩、砂岩、粉砂岩和泥岩等多种岩性岩体并通过原位试验获得这种复杂组合岩体的综合变形模量。
目前,国内外尚无非均质地基的定量判定标准,相关的研究成果也很鲜见,因此,对非均质地基的定量判定标准进行研究十分必要,也具有较大的工程意义。本文根据大量典型场地的勘察资料,获得场地剪切波速、岩体力学特性与场地非均质性之间的关系,确定了非均质场地的定量判定标准,并利用有限元软件对提出的非均质地基判定标准进行了验证和修正。
1 非均质地基的判定方法
1.1 剪切波速判定地基的均质性
根据收集的诸多场地的勘察资料,特别是地球物理勘探与地质钻探结果,发现剪切波速的差异与地基均质性之间存在着较高的相关关系。在统计一些场地的资料后发现,若场地中某一地层的剪切波速小于场地的平均剪切波速,则该层岩石质量较差,场地可以判定为非均质地基。
从收集的资料来看,场地的剪切波速平均值一般应>750 m/s,部分成岩时代较晚的沉积岩波速也应>700 m/s。如果岩体的剪切波速值较平均值小得多,则认为其质量较差[9]。对比分析一些场地剪切波速和场地的实际条件,当地基影响范围内的剪切波速值小于0.8倍的波速平均值的岩石段长度大于总深度的8%时,该场地可以判定为非均质,判定公式如式(1)所示。
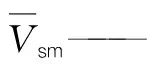
1.2 岩体力学特性判断地基的均质性
在沉积岩地区,往往是多种岩性共生,或者是以一种或两种岩性为主,伴生有其他岩性,诸多岩性形成互层、夹层等地层,接触形式也多种多样。基底平面范围内有时会由几种岩性组成,每种岩性的物理力学性状存在差异,导致地基的受力不均匀,在建筑物基础上容易产生应力集中,对上部建筑物的安全不利。因此,由力学性质差异较大的两种或几种岩石构成的地基是一种典型的非均质地基。
一般认为,当两种岩性的力学指标单轴饱和抗压强度平均值的差值>20%时,就认为两种岩性存在明显差异,并且定义单轴饱和抗压强度较低的岩层相对于单轴饱和抗压强度较高的岩层为次要岩性。对比分析大量场地岩层的单轴饱和抗压强度和场地的实际条件,发现场地中次要岩体体量占总体量的比例与场地的均质性之间存在一定的关系,如果当场地的次要岩性体量超过总体量的8%时,该场地应判定为非均质地基。
2 判定方法的有限元验证
为验证上述非均质地基的判定方法,选择有限元分析软件ABAQUS对上述两种非均质地基的判定方法进行验证,以数值分析的结果验证上述判定标准的合理性[10]。
在利用有限元进行数值计算中,以地基极限承载力作为衡量场地均质性的指标,并通过计算地基极限承载力的变化来判定地基的非均质性[11]。为此我们建立了一个二维有限元模型,设定材料为各相同性的弹塑性体,为简化建模,假设地基由两层地层组成。通过控制低剪切波速岩石段长度占总深度的比例和次要岩体体量占总体量的比例,寻找地基极限承载力发生较大变化时的低剪切波速岩石段长度占总深度的比例和软弱岩体体量占总体量的比例,该比例可以作为判定非均质地基的标准。由于建立的模型是二维的,因此, 低剪切波速岩石段长度占总深度的比例和软弱岩体体量占总体量的比例由低剪切波速岩层和软弱岩层的厚度控制。
2.1 剪切波速判识标准验证
2.1.1 参数选取和模型建立
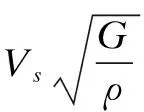
数值分析中建立的二维有限元模型如图1所示,模型中的地层分为上中下三层,其中中层地层模拟的是软弱夹层,剪切波速为Vs1,厚度为H1,上下地层为同种岩层,剪切波速为Vs2,厚度之和为H2,整个模拟地层的总厚度为H,满足H=H1+H2。
在模型的上表面中部(图中红点)处施加荷载,并在这一点处监测地表的实时沉降量,根据监测的实时数据绘制荷载沉降曲线,用于确定地基的极限承载力。

图1 二维有限元模型图
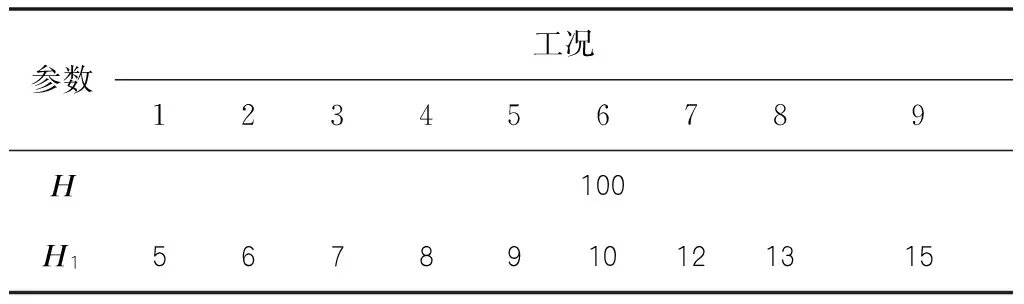
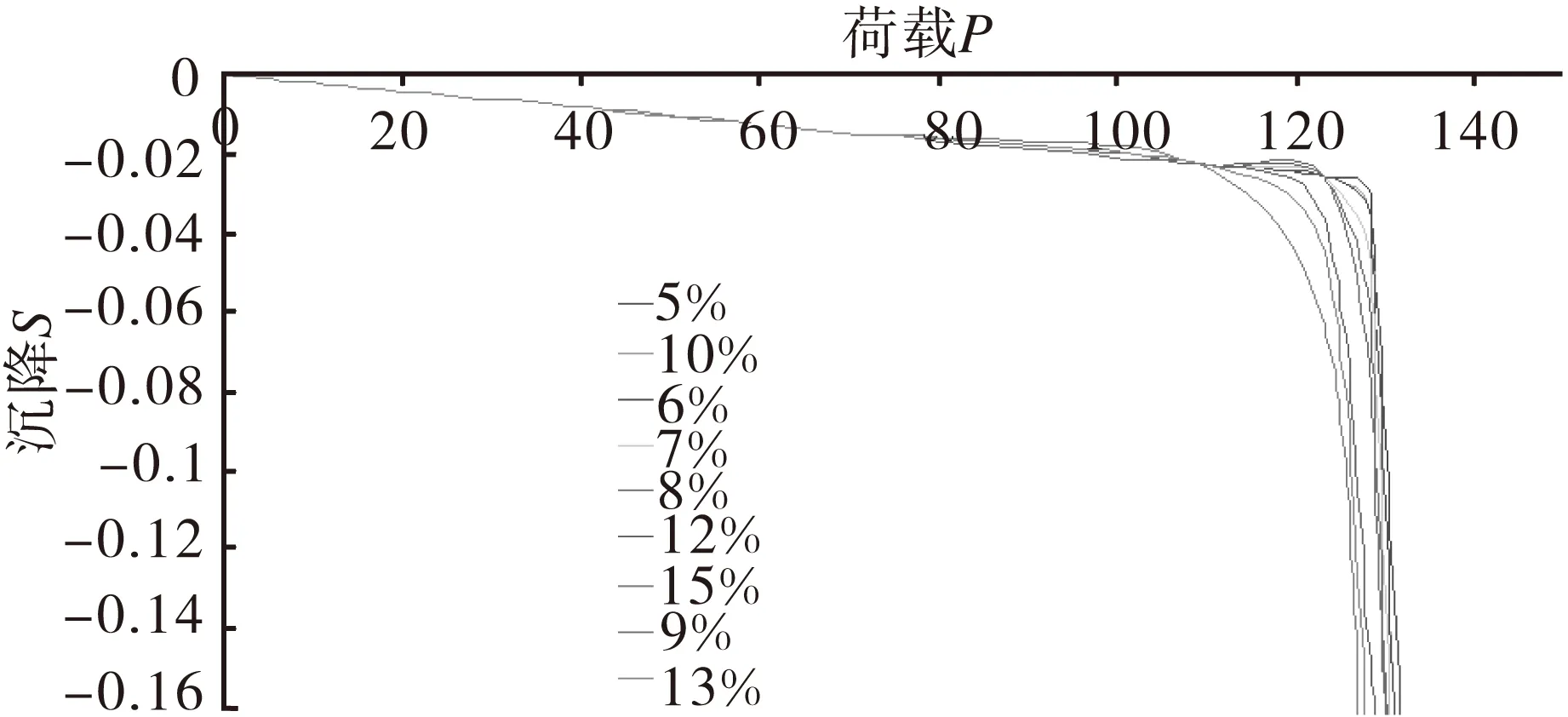
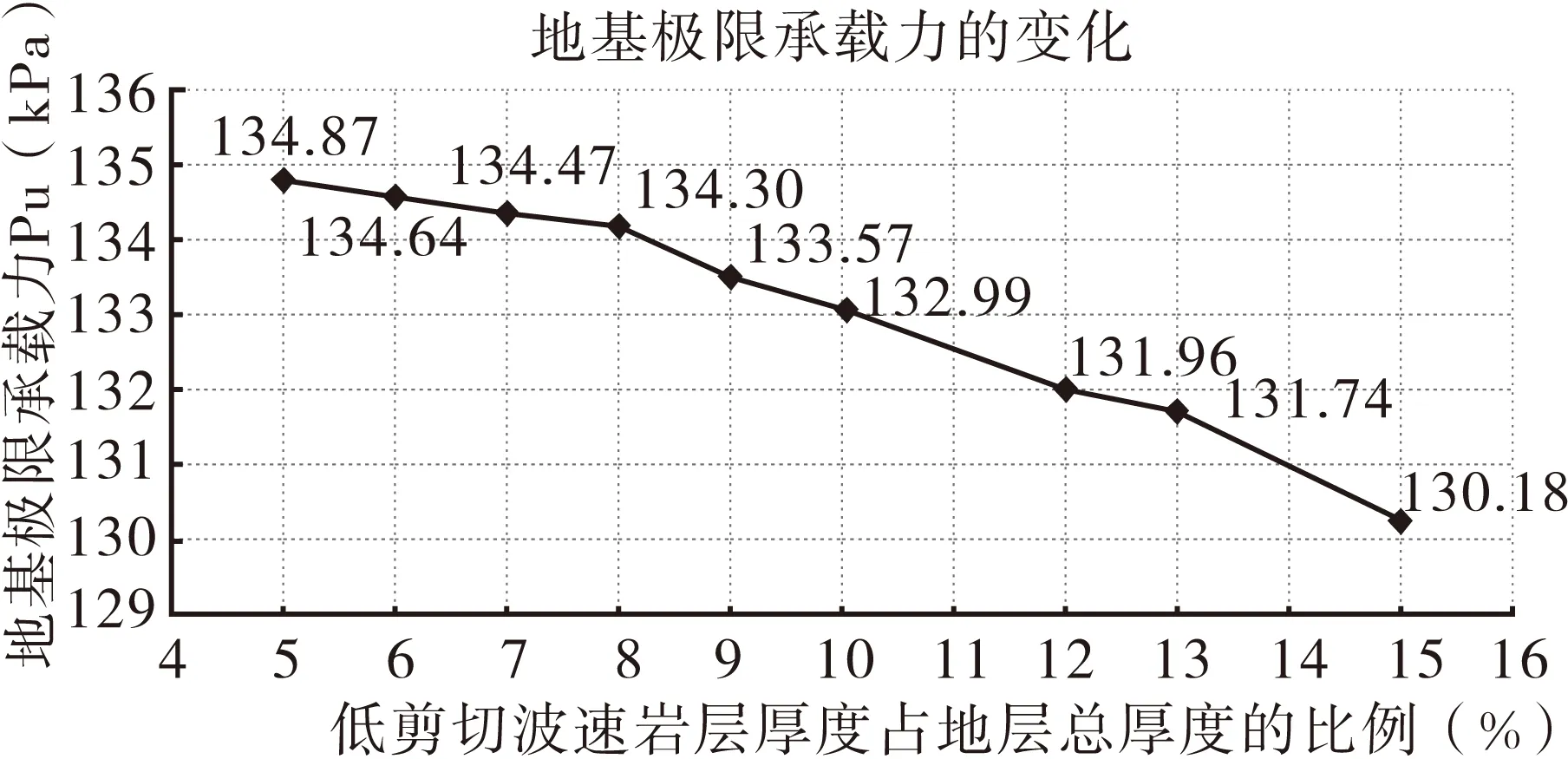
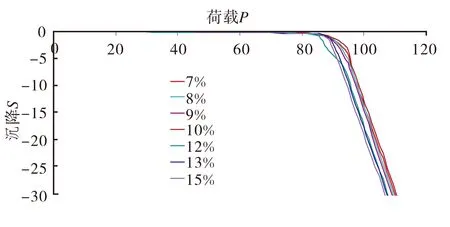
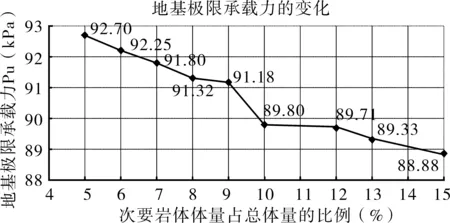
分析中假定中部地层材料模拟的是软弱夹层,即假设Vs1 (3) 得到3Vs1<2Vs1 (4) 将式(2)带入(4),可以得到: 8E1ρ2<4E2ρ1 (5) 为使ρ和E的取值满足式(5),取ρ1=2 000 kg/m3,ρ2=2 200kg/m3,E1=500kPa,E2=1 250 kPa。在数值模拟的过程中取μ=0.3。 2.1.2 计算工况 将地基影响深度范围内剪切波速值<0.8倍的平均值的岩石段长度之和占总深度的比例作为研究的对象,并将这一比例选为模型的计算工况,研究这一比例取不同的值时地基的极限承载力的变化,数值分析中选取的计算工况如表1所示。 表1 计算工况表 2.1.3 数值分析结果 利用ABAQUS计算得到的地基荷载沉降曲线如图2所示。 图2 荷载沉降曲线图 根据图2所示的荷载沉降曲线,做出地基的极限承载力随地基影响深度范围内剪切波速值<0.8倍的平均值的岩石段长度之和(H1)占总深度(H)的比例的变化曲线,如图3所示。 图3 地基极限承载力的变化规律曲线图 从图3可以看出,曲线斜率在低剪切波速层厚度占地层总厚度的比例为8%时发生了变化,当这个比例为5%~8%时,地基承载力的变化十分小,平均变化比例为1.427%,而当这一比例从8%变为9%时,承载力发生了较大的变化,变化比例为5.37%,并且从此之后随着这一比例的增大,地基的极限承载力按照5%左右的比例降低。 根据以上的数值分析结果,可以得出这样的结论:地基影响深度范围内剪切波速值<0.8倍的平均值的岩石段长度之和大于总深度的8%时地基的极限承载力将发生较大的变化,满足这一条件的场地可以判定为非均质地基。 2.2 岩体力学特性判定标准验证 2.2.1 参数选取和模型建立 本文选择单轴抗压强度Rc作为判定岩性是否存在明显差异的衡量指标。但是,在利用ABAQUS进行有限元模拟时,无法直接给材料赋予单轴抗压强度Rc进行计算,需要将Rc转换为其他参数。已有的统计结果表明岩体的单轴抗压强度和弹性模量E之间存在模糊的正相关关系,在数值分析的过程中,通过将Rc转换为E并将E赋给岩层材料进行计算。 何鹏等[12]统计了300余个沉积岩试件的测试数据,得到了不同岩性、不同构造的岩体单轴抗压强度和弹性模量之间的关系,本文选择拟合相关性系数最高、统计样本最多的统计关系式作为Rc和E之间的转换关系,这个转换关系为: E=0.092 4Rc1.133 9(R2=0.926 9,N=52) (6) 式(6)是对层理裂隙不发育的泥岩试件测试数据统计得到的,式中R代表相关性系数,N代表统计样本个数。 根据四川南充电厂泥岩的勘察数据,对于软岩层,Rc1=7 000kPa,对于较硬岩层,Rc2=10 000kPa,两者满足强度差值>20%,将Rc1、Rc2带入式(6)可得: E1=839.3kPa,E2=1 257.7kPa 数值分析中建立的二维有限元模型如上页图1所示,模型中的地层分为上中下三层,其中中层地层模拟的是软弱岩层,弹性模量为E1,厚度为H1,上下地层为同种岩层,弹性模量为E2,厚度之和为H2,整个模拟地层的总厚度为H,满足H=H1+H2。 在模型的上表面中部(图中红点)处施加荷载,并在这一点处监测地表的实时沉降量,根据监测的实时数据绘制荷载沉降曲线,进而确定地基的极限承载力。 2.2.2 计算工况 将地基平面范围内次要岩性体量之和占总体量的比例作为研究对象,研究在不同比例时地基的极限承载力的变化。针对本文建立的二维有限元模型,地基平面范围内次要岩性体量之和占总体量的比例表现为软弱岩层占模型总厚度的比例,分析中的计算工况如上页表1所示。 2.2.3 数值分析结果 利用ABAQUS计算得到的地基荷载沉降曲线如图4所示。 图4 荷载沉降曲线图 根据以上荷载沉降曲线得到地基的极限承载力,做出地基的极限承载力随地基平面范围内次要岩体体量之和占总体量的比例的变化曲线如图5所示。 图5 地基极限承载力的变化规律曲线图 从图5中可以看出,地基的极限承载力在次要岩体体量占总体量的比例为5%~9%时变化的比例较小,平均变化比例为0.412 1%;当次要岩体体量占总体量的比例达到10%时,地基的极限承载力发生了较大的变化,变化比例为1.515 6%,可以认为此时地基体现出了非均质特性,即当地基平面范围内次要岩性体量之和占总体量的比例>9%时,便可以判定该场地为非均质地基。数值计算的结果与上文提出的判定标准有1%的差异,出现这一差异的原因既可能是因为在数值计算时用E代替了Rc,而E和Rc的关系是基于大量的统计数据得到的;也可能是因为用岩体的单轴抗压强度代替了岩体的单轴饱和抗压强度。结合上文对比分析场地岩层的单轴饱和抗压强度和场地的实际条件提出的非均质地基判识方法,可以得出这样的结论:当场地一般次要岩性体量超过总体量的8%~9%时,该场地应判定为非均质地基。 根据以上分析,可以得到以下结论: (1)当地基影响深度范围内剪切波速值<0.8倍的平均值的岩石段长度之和大于总深度的8%时,场地可以判定为非均质地基。 (2)当场地一般次要岩体体量超过总体量的8%~9%时,该场地应判定为非均质地基。 本文提出了非均质地基的定量判定方法,为非均质地基的判定提供了定量的方法,具有较大的工程适用价值。 [1]GB51041-2014,核电厂岩土工程勘察规范[S]. [2]JGJ72-2004,高层建筑岩土工程勘察规程[S]. [3]姬亦工.层状非均质地基及其与多块板相互作用和反分析研究[D].大连:大连理工大学, 2000. [4]屠 晟.变值载荷作用下非均质地基的安定分析及其应用[D].大连:大连理工大学,2001. [5]彭 彬.消力池位移与应力三维有限元分析[J].广西水利水电,2004(增刊):22-26. [6]M.M.格里申.岩基中地质构造的特性对坝的强度和稳定的影响[J].华水科技情报,1981(1):27-33. [7]唐良琴,聂德新,刘东燕,余先华.软弱夹层强度参数的主要影响因素分析[J].工程地质学报,2012,20(2):289-295. [8]刘 彬,聂德新,张 勇,等.软硬相间层状复杂岩体综合变形模量原位试验研究[J].工程地质学报,2010,18(4):538-542. [9]王广军.层状地基剪切波速的统计关系[J].工程勘察,1982(2):26-29. [10]石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006. [11]张 威,李 丽,徐则民.昔格达组地层承载力综合试验研究[J].路基工程,2012(4):23-26. [12]何 鹏,刘长武,王 探,等.沉积岩单轴抗压强度与弹性模量关系研究[J]. 四川大学学报(工程科学版),2011,43(4):7-12. Research on Determination Criteria of Heterogeneous Foundation KONG Tao (Xinjiang Transportation Planning Surveying and Design Institute,Urumqi,Xinjiang,830006) Heterogeneous foundation is a common foundation,which has a greater impact on the safety and stability of buildings thereon.For the heterogeneity of foundation,there is currently no quantitative determination method.Based on a number of shear wave velocity and rock mechanics properties and other actual measurement data of typical fields,this article proposed the quantitative determination criteria of heteroge-neous foundation,and established the simplified two-dimensional model by using the ABAQUS finite element software,then with the ultimate bearing capacity as the measurement index of foundation heterogeneity,it calculated the ultimate bearing capacity of simulation fields,while according to calculation results,the pro-posed determination criteria were validated and adjusted. Heterogeneous foundation;Quantitative;Determination criteria;ABAQUS U416.1 A 10.13282/j.cnki.wccst.2015.06.008 1673-4874(2015)06-0031-04 2015-05-03 孔 滔,硕士,主要从事公路勘察方面的工作和研究。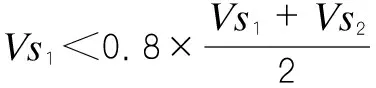
3 结语
