半刚性路面Top-Down裂缝及其应力强度因子分析

莫仕步，黄 松，王秋敏

(1.广西长长路桥建设有限公司，广西 南宁 530011；2.广西道路结构与材料重点实验室，广西 南宁 530007；3.广西交通科学研究院，广西 南宁 530007)

半刚性路面Top-Down裂缝及其应力强度因子分析

莫仕步1，黄 松2,3，王秋敏2,3

(1.广西长长路桥建设有限公司，广西 南宁 530011；2.广西道路结构与材料重点实验室，广西 南宁 530007；3.广西交通科学研究院，广西 南宁 530007)

为了研究荷载应力和温度应力对半刚性沥青路面Top-Down裂缝扩展的影响，文章基于断裂力学理论，运用有限元方法，建立弹性层状连续的二维路面结构模型，分析高温状况荷载的超载比例、既有裂缝长度和低温状况既有裂缝长度对裂缝尖端应力强度因子的影响，计算时考虑了路面非均匀温度场和温度与沥青混合料弹性模量关系。结果表明超载比例增加、既有裂缝长度增加都会导致裂缝尖端的应力强度因子线性增加，低温状况温度应力作用比高温状况荷载应力作用更易加速Top-Down裂缝的扩展。

Top-Down裂缝；路面温度场；应力强度因子；荷载应力；温度应力

0 引言

路面表面直接承受车辆荷载和环境的作用，荷载应力和温度应力使得路面表面长期处于反复受剪和受拉状况，同时路表在环境的直接作用下易老化，其老化后的抗疲劳能力变差，容易导致路面表面产生疲劳开裂，即Top-down裂缝。此外，裂缝呈上宽下

窄的V型发育，雨水易积留在裂缝尖端进一步加快Top-down裂缝的扩展速度。

半刚性基层沥青路面Top-down裂缝的影响因素众多，许多学者的研究结论也不一致，其中主要包括：重载造成的荷载应力、温度应力、沥青的老化、施工离析等。文献1[1]运用有限元方法对Top-down裂缝开裂原因进行研究，认为荷载应力是导致Top-down产生的主要原因，而环境变化只是加速了Top-down裂缝的扩展。文献2[2]通过对裂缝开裂机理的研究，认为低温状况下沥青层的温度应力是导致Top-down裂缝产生的主因。文献3[3]采用有限元分析方法对不同路面结构进行力学分析，认为高温状况下的荷载应力和低温状况下的温度应力是导致Top-down裂缝产生的主要原因。文献4[4]利用有限元方法和断裂力学理论，计算Top-down裂缝尖端的应力强度因子，结果表明荷载引起的剪应力是造成路表裂缝扩展的主因。文献5[5]认为路表沥青混合料的老化程度、铺面离析程度、局部轮载的集中作用和温缩应力对裂缝的产生和扩展有显著影响。文献6[6]认为Top-down裂缝是表面层结构内部存在的微裂缝在拉应力作用下扩展形成的，同时荷载大小和荷载位置对裂缝扩展作用很大，温度应力和老化作用对裂缝的扩展作用也很大。综上所述，影响Top-down裂缝断裂和扩展的因素主要有荷载应力和温度应力，荷载应力主要是高温状况局部轮载引起的剪应力，而温度应力则是低温状况的温缩应力，而且不同温况沥青混合料的弹性模量差异较大。因此，在进行荷载应力和温度应力计算时应考虑温度对沥青层模量的影响。

实际路面温度场是一个非均匀的温度场，距路表越近其受环境影响越大，即沿路面深度方向存在温度梯度，所以非均匀温度场变化较均匀温度场变化引起的温度应力更接近实际情况。此外，沥青混合料是一种温度敏感性材料，弹性模量随温度变化较大，在进行路面结构计算时应结合温度场的分布对其弹性模量进行修正。因此，本文采用有限元方法和断裂力学理论，根据气象参数确定路面非均布温度场，结合沥青混合料弹性模量与温度的关系，分析车辆荷载和温度作用对Top-down裂缝尖端应力强度因子的影响规律。

1 路面温度场分析

为了模拟高温状况轮载作用下的剪应力和低温状况温度应力对Top-down裂缝尖端应力强度因子的影响，本文根据极限状态设计方法，分别模拟了最不利高温、低温状况路面温度场的分布及其日变化规律。关于半刚性路面结构层的热特性参数参考文献7[7]，且不考虑温度对各热特性参数的影响。根据中国气象数据网的统计资料，拟定最不利高温、低温状况的气象参数见表1。

表1 最不利温况的气象参数表

本文运用限元通用计算软件ABAQUS建立路面二维平面模型，模型尺寸为(3×6)m，即路面深度为3 m，宽为6 m，选用DC2D8八节点四边形单元进行单元网格划分，通过ABAQUS用户子程序FILM和DFLUX实现太阳辐射、对流交换等热边界条件。为了确保初始温度场的准确性，建立两个24 h的瞬态热传导分析步，时间增量步均为0.5 h，其中第一个分析步的最后一个增量步温度场计算结果作为第二个瞬态分析步的初始条件。高温、低温状况路面结构沥青层的温度场及其日变化规律见图1和图2。

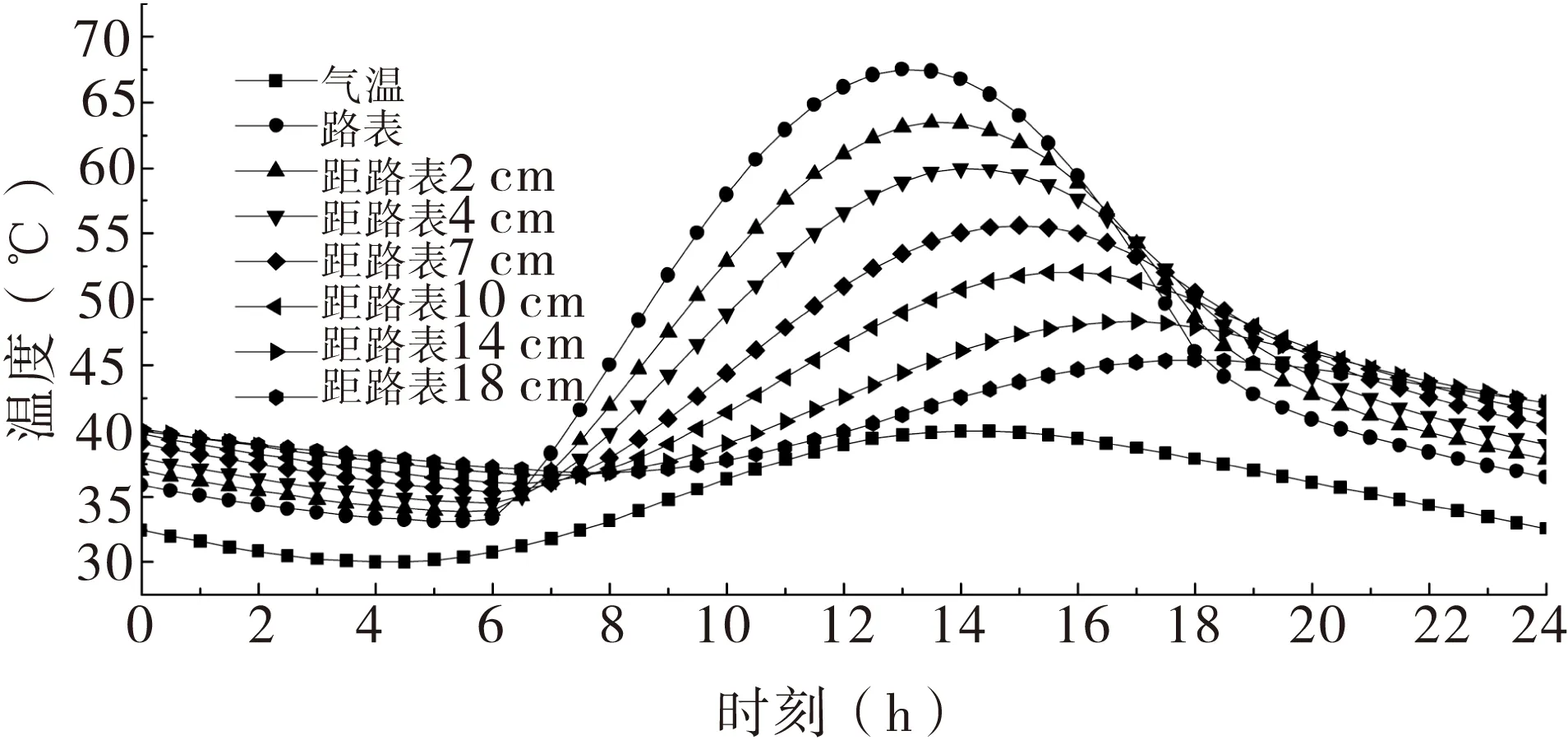
图1 高温状况沥青层不同深度处温度的日变化规律曲线图

从图1的计算结果可知，高温状况路面各深度处温度均随气温呈周期性变化，路表日最高温度达67.5 ℃，出现的时刻为13：00，其日最大变温幅度为34.4 ℃，比气温的日最大变温幅度大了24.4 ℃，这主要是因为太阳辐射的作用太强，路表吸收热量多。沥青层厚度对温度具有削减作用，即随着深度增加，沥青层各时刻的温度不断减小，并在13：00左右温度梯度达到最大，沥青层各时刻的温度均高于气温。

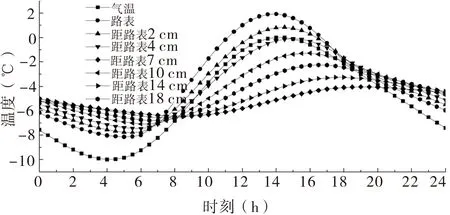
图2 低温状况沥青层不同深度处温度的日变化规律曲线图

从上页图2的计算结果可知，低温状况路面各深度处温度均随气温呈周期性变化，路表日最高温度为1.9 ℃，出现的时刻为14：00，其日最大变温幅度为10.1 ℃，和气温的日最大变温幅度接近，这是因为低温状况太阳辐射作用弱，路表吸收的热量较少。与高温状况一致，随着沥青层深度增加，温度不断降低，并在14：00时刻温度梯度最大，气温在夜间都低于沥青层的温度，这也是因为正午是太阳辐射最强的时候，而夜间太阳辐射基本为零。

2 沥青混合料弹性模量温度修正

温度是导致路表Top-down裂缝不断扩展不可忽略的因素。从前文计算结果可知，不同温况和同一温况不同时刻下路面的温度场都是不一样的，因此，在温度变化过程中不仅会导致路面结构沿厚度方向变形不协调而产生温度应力，同时沥青混合料是一种温度敏感性材料，其弹性模量随温度的变化较大，特别在不同温况下，弹性模量的变化将使路面应力发生重分布。所以，有必要根据沥青层不同深度处的即时温度，对该处混合料的模量进行修正。

文献8[8]提出BELLS沥青层模量修正模型，结果表明该计算结果与室内动态模量试验结果非常接近，同时文献9[9]等人根据实测结果证明该结果的稳定性，BELLS沥青层模量修正模型的公式如式(1)所示，因此，本文采用该式进行低温状况沥青层模量的修正。

ET=E20×100.018(20-T)(1)

式中：ET——T℃时沥青层的反算模量；E20——20 ℃时沥青层的参考模量；T——温度(℃)

本文假设20 ℃时沥青层的参考模量为1 400MPa，则其他温度状况下，沥青层的弹性模量见图3。从图3中沥青混合料随温度的变化规律可知，温度从-10 ℃升高至70 ℃，沥青混合料的弹性模量则从4 854MPa降低至176MPa，相差约27.6倍，说明了对沥青路面进行结构力学计算，温度是非常关键的因素。

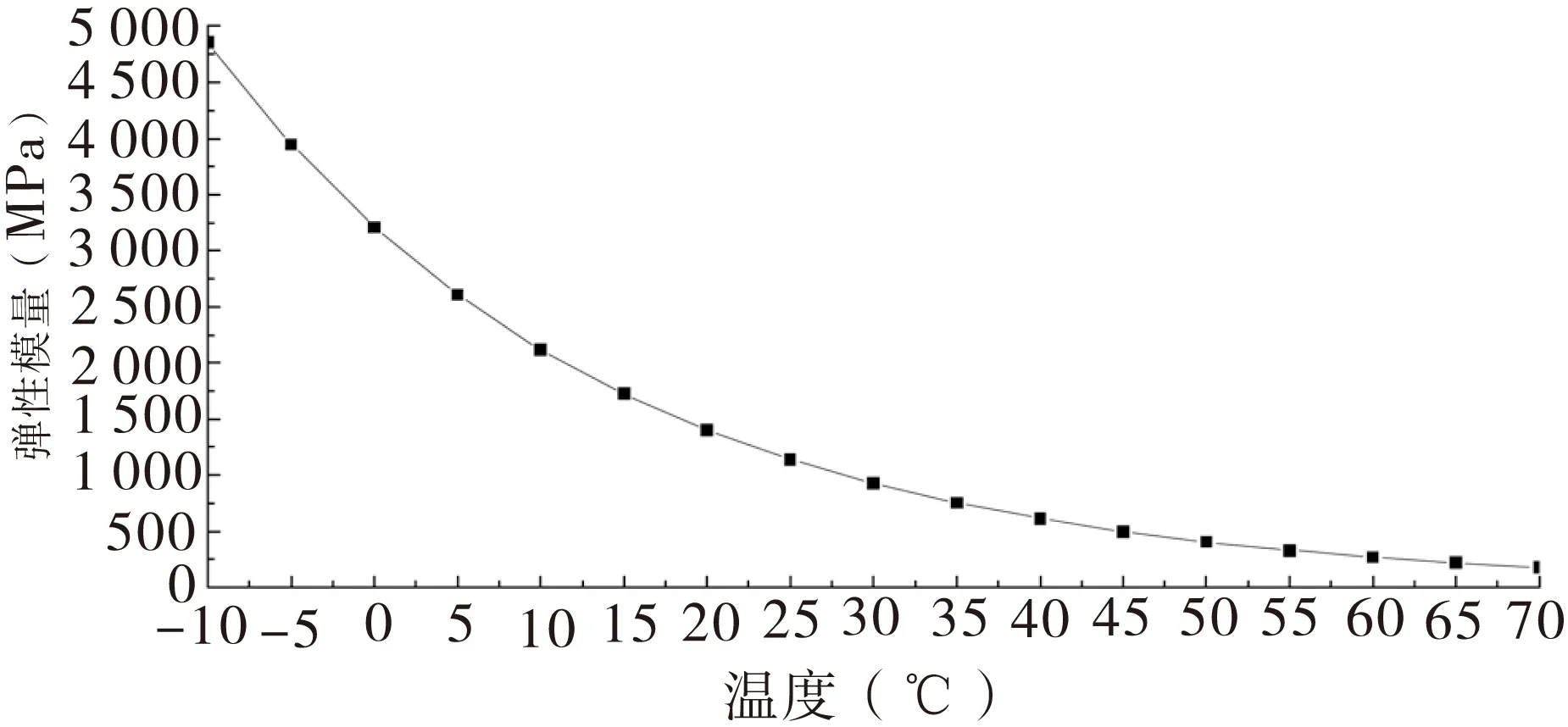
图3 不同温度状况下沥青层的弹性模量变化规律曲线图

因此，本文在计算荷载应力和温度应力时将计算时刻的路面温度场作为预定义场倒入计算模型，将沥青层材料属性的弹性模量定义为如式(1)的温度模量函数，软件将根据温度对模量进行赋值。

3 荷载应力对Top-down裂缝的影响

裂缝尖端的应力场是奇异场，即只要荷载存在，应力就趋于无穷大，利用有限元方法进行裂缝尖端的力学分析时，裂缝尖端处的应力将不收敛于网格尺寸，即网格尺寸越小，计算应力值越大，说明采用应力作为控制指标所建立的强度判据，不能反映含裂缝路面结构的实际承载能力。

应力强度因子作为裂纹尖端附近应力奇异性程度的表征参量，是衡量裂纹尖端应力场强度的重要指标，它是以数值来表示不同裂缝尖端趋向开裂的程度，应力强度因子越大，裂缝越可能出现失稳扩展，裂缝疲劳扩展速度也就越快，导致其疲劳寿命越短。因此，在断裂力学中，它被用来作为衡量裂缝是否发生失稳扩展的标准。

本文采用二维有限元模型作为路面结构的计算模型，其模型参数见表2。边界条件为模型两侧水平约束，模型底部全约束。为了提高计算精度对裂缝尖端进行网格细化，并对裂缝尖端进行奇异网格划分，见图4，其单元类型为CPE8(八节点二次平面应变单元)。

表2 路面结构和材料参数表

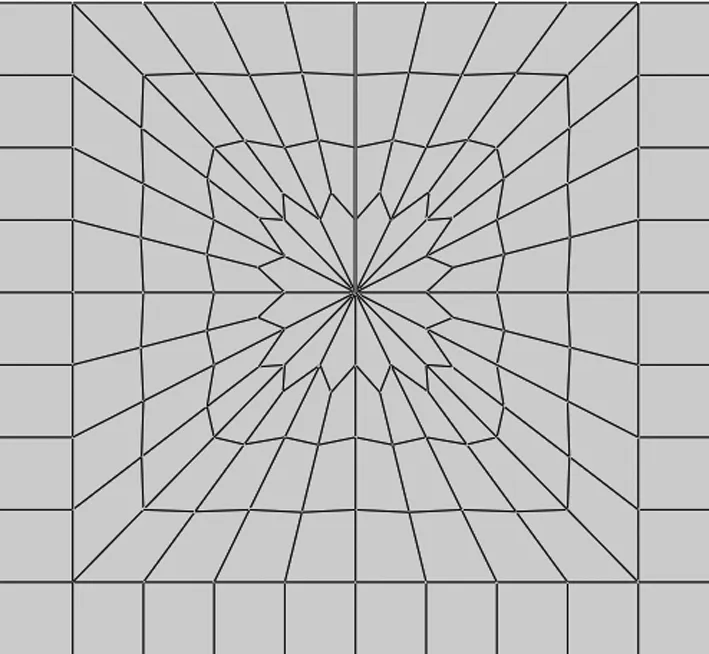
图4 裂缝尖端的奇异网格划分图

经计算，裂缝尖端在对称荷载作用下，KⅠ<0，KⅡ=0，裂缝尖端受压，属于闭合状态，说明对称荷载对于裂缝的扩展没有任何贡献。而裂缝尖端在偏载作用下，如图5所示，KⅠ<0，KⅡ>0，裂缝尖端虽然不会产生张开型裂缝，但是由于荷载作用于裂缝的一侧，裂缝的两侧面将有相对滑移趋势，因此偏载作用将使裂缝发生剪切型扩展，而且轮载经过一道裂缝会产生两次方向相反的剪切作用。因此，本本采用偏载作为不利荷位。

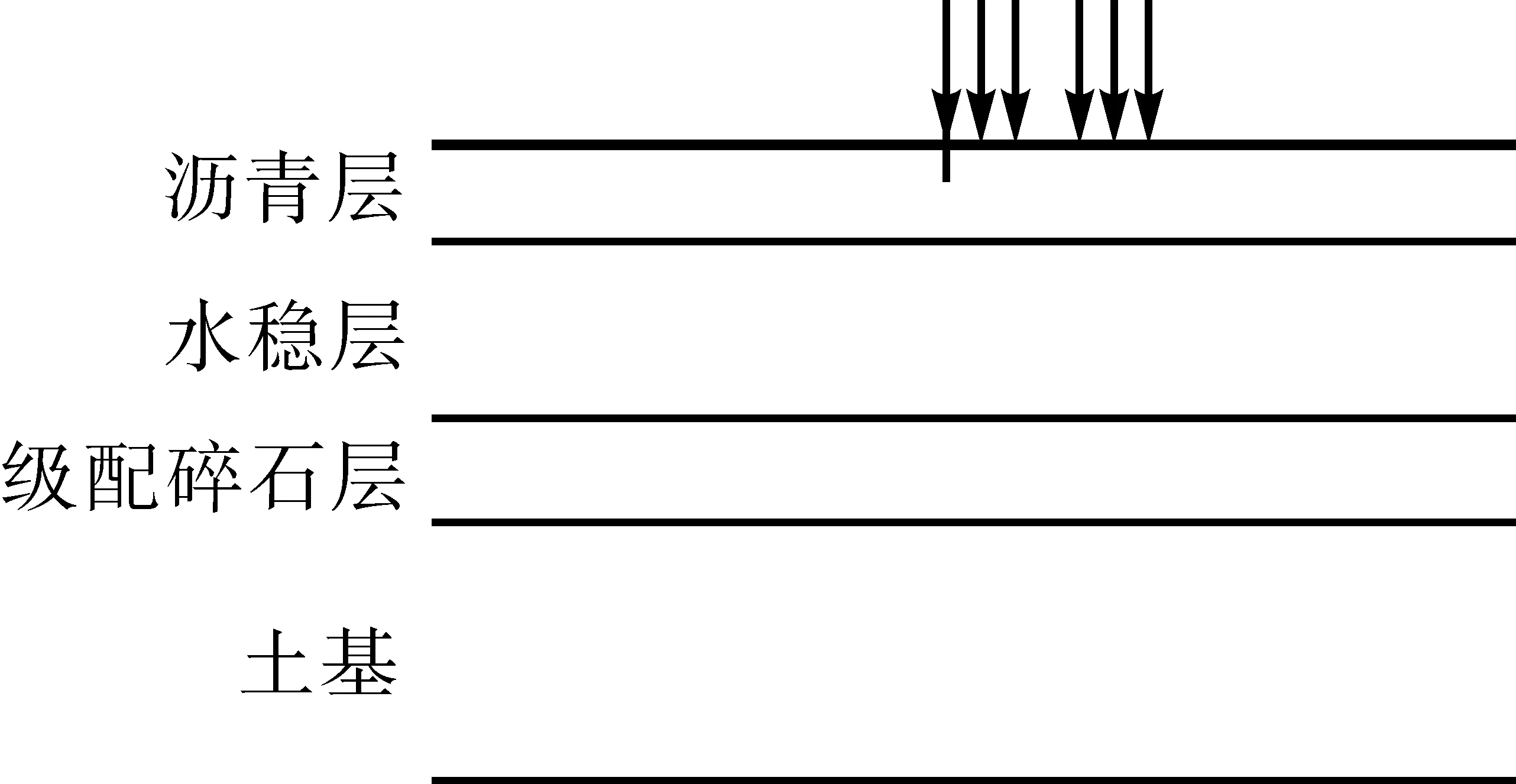
图5 偏载作用示意图

为了进一步研究荷载应力作用对裂缝扩展的影响，本文计算了不同超载比例条件下裂缝尖端的剪切型应力强度因子KⅡ，超载比例包括25%、50%、75%和100%，同时还计算了各超载比例作用下不同的Top-down裂缝长度的KⅡ的变化规律，裂缝长度包括2cm、4cm、7cm、10cm和14cm，计算结果见图6。

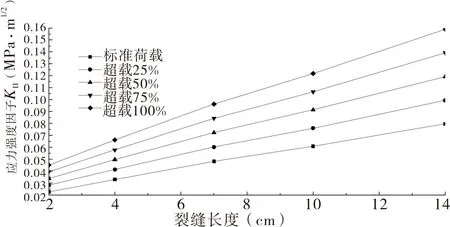
图6 不同超载条件下KⅡ随裂缝长度的变化规律示意图

从图6的计算结果可知，高温状况不同荷载作用下，Top-down裂缝尖端的应力强度因子KⅡ均随着该裂缝的长度基本呈线性增长，裂缝长度由2cm扩展至14cm，标准荷载作用下KⅡ由0.022 6MPa·m1/2增大至0.079 6MPa·m1/2，增大了0.057MPa·m1/2，超载100%作用下KⅡ由0.045 2MPa·m1/2增大至0.159 1MPa·m1/2，增大了0.113 9MPa·m1/2。 可见裂缝长度由2cm扩展至14cm，KⅡ增大了2.52倍；荷载由标准轴载增大至超载100%，KⅡ增大了约2倍。说明高温状况下Top-down裂缝长度和荷载的超载比例对裂缝的进一步扩展影响较大，因为裂缝长度越长，裂缝两侧的传荷能力越差，偏载作用下裂缝两侧相对滑移的趋势越大，所以裂缝尖端剪应力集中程度越高；荷载越大，偏载作用使裂缝两侧的竖向位移变形相差越大，同样裂缝尖端受到的上下剪切作用越强。

4 温度应力对Top-down裂缝的影响

从前文可知，气温在不同时刻一直都在变化，由于热传导的时效性和结构层对温度的削减作用，路面沿深度方向的变温幅度不一致，距路表越近其变温幅度越大。此外，沥青层的线膨胀系数是水稳基层和级配垫层的约2倍。因此，在降温作用下，路面上层的收缩变形量将大于下层，对于层间连续状态的路面结构，下层的小变形将约束上层的大变形，上层的收缩变形受到约束，从而产生了温度应力。对于升温阶段，沥青层由于膨胀受到约束，属于受压状态，所以不考虑其温度应力。

温度应力属于水平力，不会对裂缝尖端产生剪切作用，只有拉伸作用，因此只会使裂缝发生张开型扩展。本文将依据极限状态设计方法，计算低温状况降温条件下带Top-down裂缝路面结构的张开型应力强度因子KⅠ，即以路表日最高温度时刻路面温度场为计算起点，并假设此刻温度应力为零，然后以路表日最低温时刻路面温度场为计算终点，计算这两个时刻的降温作用引起的温度应力。因为低温状况沥青混合料的弹性模量高，呈脆性材料，应力松弛能力弱，所以不考虑应力松弛作用。同时根据前文低温状况路面结构温度场和温度与沥青混合料模量的函数关系式，对低温状况下的沥青材料进行模量赋值。因为高温状况沥青混合料的弹性模量比低温状况低了20多倍，且高温状况沥青混合料有较强的应力松弛能力，尽管高温状况路面变温幅度大，但其温度应力小，且能被沥青面层松弛掉，所以，不考虑高温状况的温度应力。

计算低温状况温度应力时，沥青层、水稳层、级配碎石层和土基的线膨胀系数分别为2.0×10-5℃-1、1.0×10-5℃-1、0.5×10-5℃-1和0.5×10-5℃-1。其计算结果见图7。

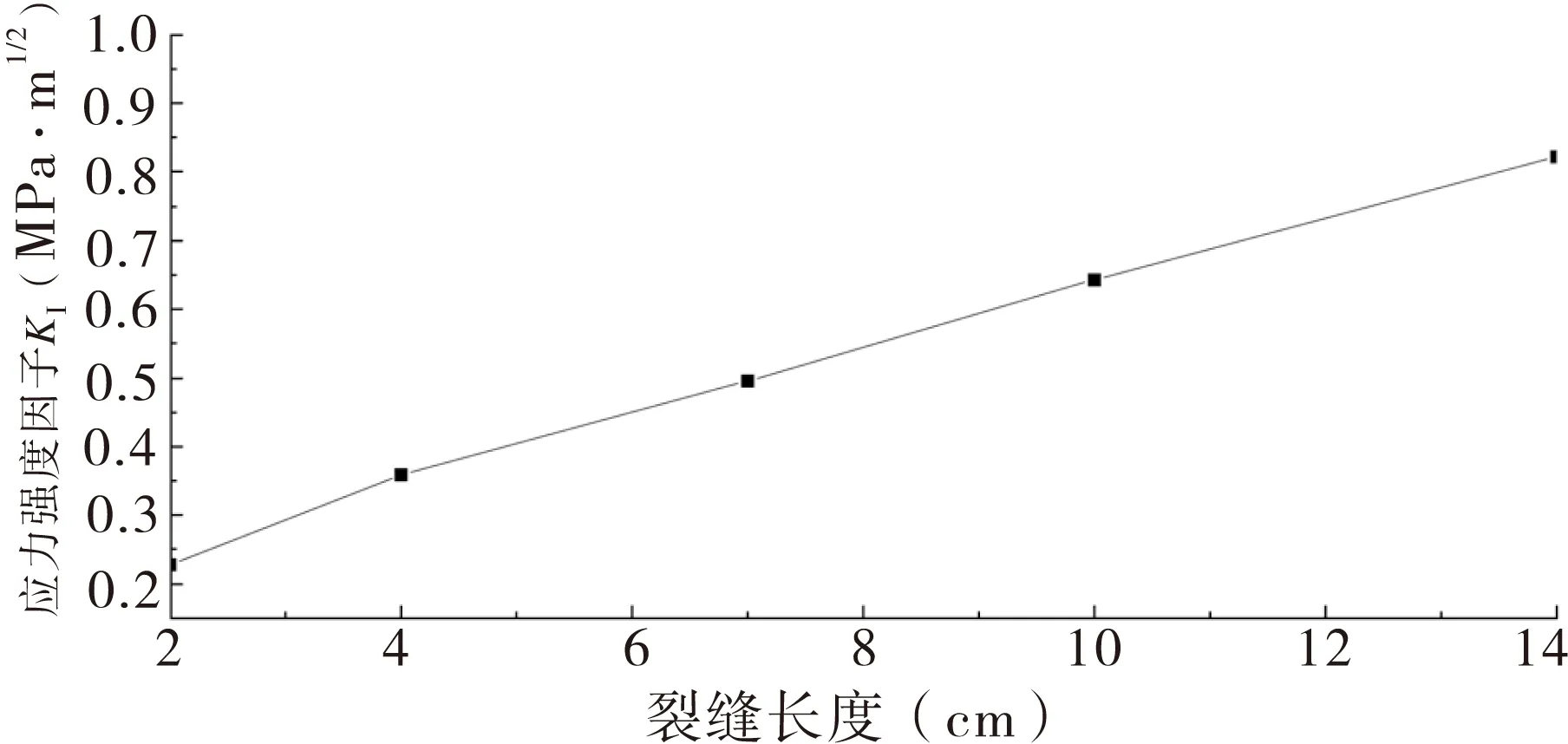
图7 温度应力作用下KⅠ对不同裂缝长度的影响规律示意图

从图7的计算结果可知，在温度应力作用下，Top-down裂缝尖端的张开型应力强度因子随着裂缝深度的增加而线性增大，说明裂缝向下扩展的速度将越来越快。当裂缝长度从2cm扩展至14cm时，KⅠ值从0.227MPa·m1/2增大至0.821 9MPa·m1/2，增大了约2.6倍。

综合比较荷载应力和温度应力计算结果可知，荷载应力主要导致Top-down裂缝发生剪切型扩展，而温度应力则导致Top-down裂缝发生张开型裂缝。两种应力作用下，裂缝尖端的应力强度因子均随裂缝的扩展长度而线性增大，说明随着裂缝的不断扩展，其扩展的速度将不断加快。从计算结果可知，低温状况温度应力作用下裂缝尖端的值要远大于高温状况荷载应力作用下裂缝尖端的KⅡ值，说明低温状况的温度应力更容易加速裂缝的扩展。

5 结语

(1) 路面各深度处温度均随气温呈周期性变化，高温状况路表日最高温度达67.5 ℃，低温状况路表日最高温度为1.9 ℃，随着沥青层深度增加，温度不断降低，并在高温时刻温度梯度最大。

(2) 温度从-10 ℃升高至70 ℃，沥青混合料的弹性模量则从485 4MPa降低至176MPa，相差约27.6倍，计算含裂缝沥青路面结构力学时，应根据路面结构温度场的分布情况，结合沥青混合料弹性模量和温度的函数关系，对路面沥青结构层进行弹性模量赋值。

(3) 高温状况荷载应力作用下，主要导致Top-down裂缝发生剪切型扩展，剪切型应力强度因子KⅡ随着裂缝深度增加而线性增大，同时也随超载比例增加而不断增大，在裂缝长度为14cm，超载比例为100%时，KⅡ值为0.159 1MPa·m1/2。

(4) 低温状况温度应力作用下，主要导致Top-down裂缝发生张开型扩展，张开型应力强度因子KⅠ随着裂缝深度的增加而线性增大，当裂缝长度为14cm时，KⅠ值为0.821 9MPa·m1/2，该值远大于高温状况荷载应力作用下裂缝尖端的KⅡ值，说明低温状况的温度应力更容易加速裂缝的扩展。

[1]Gerritsen.A.H，etal[J].PredictionandPreventionofSurfaceCrackinginAsphalticPavements，Proceedingofthe6thInternationalConferenceonAsphaltPavement，AnnArbor，1987，378-391.

[2]WangLB.MicromechanicsStudyonTop-DownCracking[J].TransportationResearchRecord，2003(1853):121-133.

[3]MYERSL，RROQUE.Top-DownCrackPropagationinBituminousPavementsandImplicationsforPavementmanagement[J].ProceedingsoftheAssociationofAsphaltPavingTechnologists，2002，71:651-670.

[4]易 昕.三维有限元方法分析沥青路面自上而下裂缝的扩展[D].长沙：湖南大学，2006.

[5]李 峰，孙立军.沥青路面Top-Down开裂成因的有限元分析[J]. 公路交通科技，2006(6):1-4.

[6]徐鸥明，郝培文.厚沥青路面Top-down裂缝分析及对路面设计的启示[J]. 中外公路，2006(5):133-137.

[7]李 辉.沥青路面车辙形成规律与温度场关系研究[D].南京：东南大学，2007.

[8]Dong-YeobPark.EffectofTemperatureandLoadingTimeontheStiffness，DoctoralDissertation[D].MichiganStateUniversity，2000.

[9]王月峰，王传沛，庄传仪.沥青混合料动态模量温度修正研究[J]. 中外公路，2012(2):210-214.

Analysis on Top-Down Cracks and Its Stress Intensity Factor of Semi-rigid Pavement

MO Shi-bu1，HUANG Song2,3，WANG Qiu-min2,3

(1.Guangxi Changchang Road and Bridge Construction Co.，Ltd.，Nanning，Guangxi，530011；2.Guangxi Key Laboratory of Road Structure and Materials，Nanning，Guangxi，530007；3.Guangxi Transportation Research Institute，Nanning，Guangxi，530007)

In order to study the impact of load stress and temperature stress on the Top-Down cracking de-velopment of semi-rigid asphalt pavement，then based on fracture mechanics theory，and by using the finite element method，this article established the continuous two-dimensional pavement structure model of elastic layers，and analyzed the influence of overloading ratio of loads under high temperature conditions，length of existing cracks，and length of existing cracks under low-temperature conditions on stress intensity factor at crack tip，and during the calculation it considered the relationship between non-uniform temperature field and temperature of pavement with the elastic modulus of asphalt mixtures.The results showed that，the increase of overload ratio and the increase of existing crack length will all lead to the linear increase of stress intensity factor at crack tip，and the temperatures stress impact under low temperature conditions more easily accel-erates the extension of Top-Down cracks than the load stress impact under high temperature conditions.

Top-Down cracks；Pavement temperature field；Stress intensity factor；Load stress；Temperature stress

U

A

10.13282/j.cnki.wccst.2015.06.006

1673-4874(2015)06-0022-05

2015-05-05

莫仕步，工程师，主要从事路桥施工管理工作。