一种改进的GPS 接收机弱信号捕获算法
2015-07-01马经纬王延东
马经纬,王延东,江 晟
(中国科学院长春光学精密机械与物理研究所,长春 130033)
GPS 是目前世界范围内发展最为完善,运行最为稳定,应用范围最广的卫星导航系统。近年来,随着GPS 产品的飞速发展和广泛应用,人们对GPS 的使用环境要求也越来越高,包括在高楼林立的城市街道、室内、停车场等卫星信号微弱的环境。因此,在弱信号环境下GPS 的卫星信号捕获问题成为了近年来的研究热点[1]。
信号捕获的主要任务是在空间中存在的众多电磁波信号中准确地识别捕获到GPS 卫星广播的信号,确定卫星信号的多普勒频移和伪码的初始相位,实现接收机本地生成的载波信号和伪码与接收到的卫星信号的粗同步,为接收机后续的信号跟踪和导航结算打下基础[2]。捕获灵敏度是指接收机能够捕获到的卫星信号的最低信噪比(SNR),是反映接收机性能的重要指标。
在弱信号捕获方面,加长相干积分时间是最有效的方法,但导航数据跳变位的存在限制了相干积分时间的加长[3]。在不知道导航数据跳变位置的情况下,相干积分时间通常不超过10ms[4]。因此,估计导航数据跳变的位置就成了弱信号捕获的关键。文献[5]中介绍了一种全比特的弱信号捕获算法,但这种算法计算量巨大,不利于工程实现。文献[6]中介绍了半比特捕获算法,并将块累加思想运用到算法中,但这种算法中采用的非相干积分累加方法会造成平方损失,不利于积分增益的提高。文献[3]中介绍了一种避免平方损失的差分累加的方法,但相干积分时间仍然限制在10 ms。
本研究对GPS 接收机的信号捕获算法进行了研究,同时在半比特捕获算法的基础上提出了一种改进的弱信号捕获算法,提高了GPS 接收机的捕获灵敏度。
1 传统的GPS 接收机捕获算法
传统的GPS 信号捕获算法主要有串行时域捕获算法和并行频域捕获算法2 种,其中,串行时域捕获算法主要应用在传统的GPS 硬件接收机中,而并行频域捕获算法主要应用于软件接收机中。由于串行时域捕获算法对卫星信号的多普勒频移和码相位进行二维搜索,搜索区间大,耗时长,因此本文主要介绍频域的并行码相位捕获算法。
并行码相位捕获算法可将码相位的搜索过程通过傅里叶变换一次性完成,因此只需要在频率范围内进行搜索即可。这种算法将与本地载波信号进行混频后的中频信号和本地C/A 码信号分别进行傅里叶变换之后共轭相乘,然后再进行傅里叶反变换,得到信号相关累积后的模值与门限值进行比较,若高于门限值则捕获成功,否则在下一频段继续捕获。其原理图如图1 所示[7]。

图1 并行码相位捕获算法原理框图
对于2 个长为N 点的周期性序列x(n)和y(n),它们的相关值z(n)为
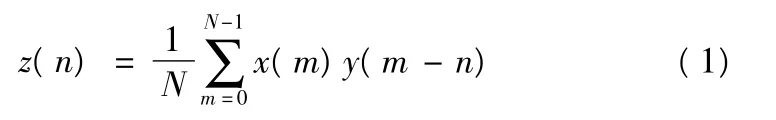
对上述相关值z(n)进行离散傅里叶变换,得到离散傅里叶变换结果如下
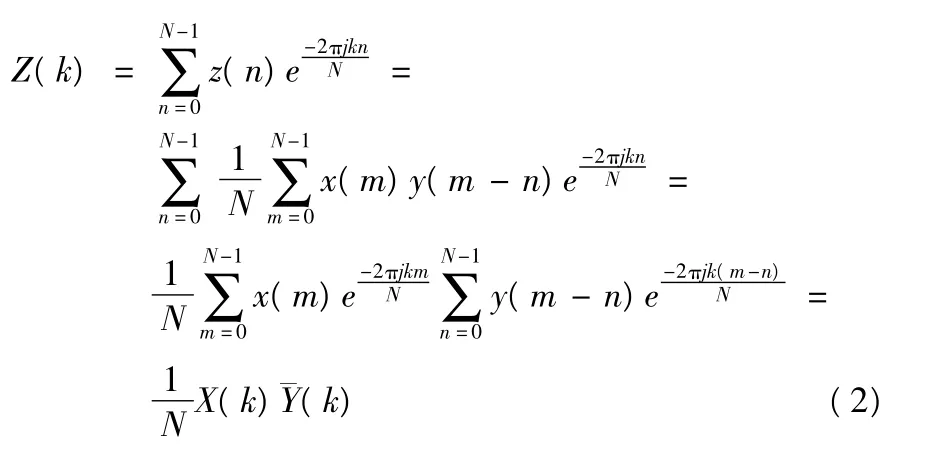
其中:X(k)和Y(k)分别为x(n)和y(n)的离散傅里叶变换;¯Y(k)表示变换结果Y(k)的共轭。若x(n)和y(n)分别代表输入的卫星信号和本地产生的伪码序列,则由式(2)可以得知,2 个序列在时域内做相关运算相当于它们的离散傅里叶变换在频域内做共轭乘积运算,因此,频域内乘积的傅里叶反变换也正代表了时域内各个码相位处的相关值。
2 改进的弱信号捕获算法
2.1 累加方法
在正常情况下接收机通常利用1 ms 的卫星信号数据便可成功的捕获到信号,即一个C/A 码的周期,无论是采用时域捕获算法或频域捕获算法均可,但在弱信号的环境下,由于有用信号的功率比较低,捕获的判决量往往达不到门限值,造成捕获的失败。因此,在这种情况下,接收机在捕获的过程中需要对几十毫秒甚至几百毫秒的卫星数据通过一定方法进行处理以得到可靠的捕获判决量。一般采用对多个C/A 码周期的相关结果进行一定的累加方式以提高微弱信号的信噪比。常用的累加方法有相干累加、非相干累加和差分累加方法[8-10],相干累加方法对信噪比提升最为明显,但其累加时间受到导航数据比特跳变和损耗因子的限制;非相干累加虽然克服了导航数据比特的跳变,但其引入了平方损失,信噪比提升有限; 差分累加的信噪比提升介于相干累加和非相干累加之间,由于其不受导航数据为跳变的影响,所以在弱信号处理过程中是一个比较好的选择。在高灵敏度接收机设计中,为了尽可能兼顾实时性,获取更高的信噪比,通常采取将这几种累积算法相结合的算法。
2.2 改进的弱信号捕获算法
半比特方法是弱信号捕获中较常用的一种算法。由于导航数据比特的宽度为20 ms,因此半比特方法将读入的卫星信号每20 ms 分成两段,前后各10 ms,这样导航数据比特的跳变肯定会落在2 个10 ms 数据块中的一个里面,从而导致含有导航跳变的数据块相干累加结果变小。对前后10 ms的数据进行相干累加,奇数段(数据段1,3,5,…)的相干结果进行非相干累加,偶数段(数据段2,4,6,…)的相干结果进行非相干累加,然后比较2 个非相干累加结果的大小。由于数据比特的宽度为20 ms,因此跳变位置只可能存在于奇数块中或者偶数块中而绝不可能同时存在于奇数块和偶数块中。因此,比较奇数块和偶数块非相干累加结果后便可以成功的避免导航数据比特跳变的影响,利用不含有导航跳变的一组数据进行捕获判决,完成卫星信号的捕获。但半比特方法有2 个明显的缺点:首先半比特方法中相干累加的时间只有10 ms,数据利用率低。其次该算法采用了非相干累加方法,捕获过程中会引入平方损耗,降低了信噪比增益。
本研究提出的弱信号捕获算法对半比特方法的2 个缺点进行改进。首先通过精确判断导航数据比特跳变位置提高其相干累加时间,同时避免导航数据比特跳变的影响; 其次利用差分累加方式代替非相干累加来避免非相干累加引入的平方损失,提高信噪比。
由于半比特方法只是确定导航数据跳变存在于哪个10 ms 的数据块当中,因此在进行捕获的过程中最长只能进行10 ms 的相干累加,而与其相邻的存在导航数据跳变的10 ms数据则只能舍弃。针对这一问题,本研究将对导航数据跳变的位置进行进一步确定,将读入的卫星数据中的每个10 ms数据再进行分块,分成2 个5 ms 的数据块,通过相干积分之后的比较进一步确定导航数据跳变位置存在于哪个5 ms 的数据之中,从而使可用于相干积分的数据长度变为15 ms,提高捕获的灵敏度。新的捕获算法数据分块图如图2 所示。
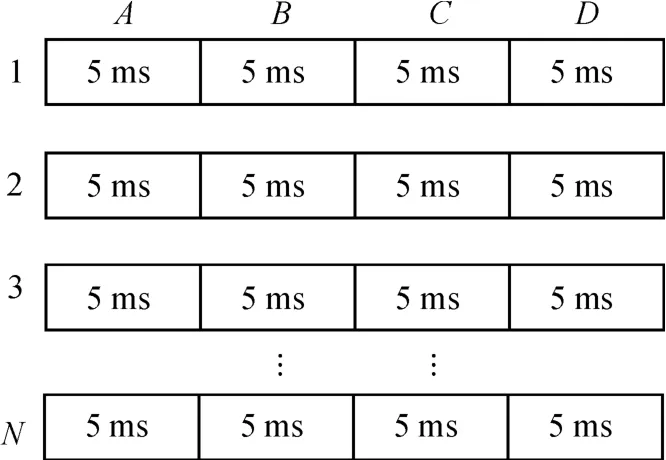
图2 改进算法数据分块
由图2 可知,改进的弱信号捕获方法读入N ×20 ms 的卫星数据,将卫星数据每20 ms 为一组,共分成N 组;接下来每一组20 ms 数据以5 ms 为单位分为4 块,分别标记为A、B、C、D。将每一个5 ms 数据块以1 ms 为单位进行数据累加,累加后的数据进行相干积分得到RAn,RBn,RCn,RDn(n =1 ~N)。由于每组数据相差时间为20 ms,即一个导航数据跳变周期,导航数据比特跳变将会发生在每组数据的相同位置的数据块内。将N 组数据中的相同位置数据块的相干累加结果进行平方相加得到4 组累加结果:
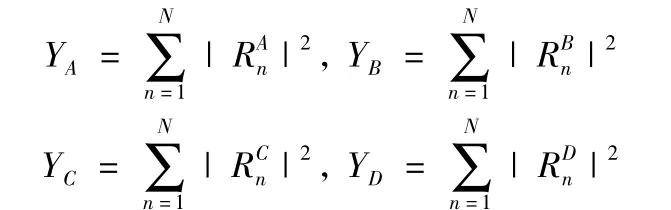
比较4 组累加结果(YA,YB,YC,YD)的大小,其中累加结果最小的一组内含有导航数据比特的跳变,因此便确定了含有导航数据比特跳变的5 ms 数据块的位置。以这个位置为边界,将处在2 个导航数据跳变位置之间的3 个数据块的相干累加结果进行相干累加。由于处在2 个导航数据跳变位置之间的数据块数据码没有跳变,即符号相同,因此得到的累加结果便相当于15 ms 的相干累加结果。接下来对每个15 ms 的相干累加结果进行差分累加,最终得到捕获检测量。下面举例说明。
若导航数据比特跳变位置发生在A 位置,则不含导航数据比特跳变的数据块累加结果依次为
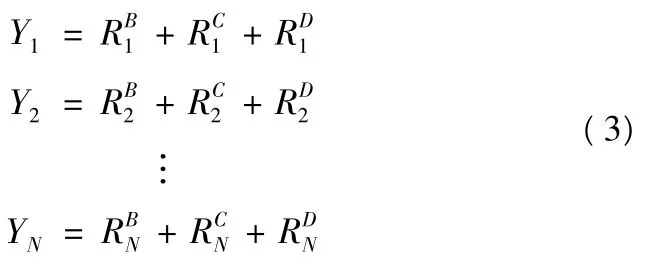
则检测统计量为

若导航数据比特跳变发生在B 位置,则不含导航数据比特跳变的数据块累加结果依次为

则检测统计量为
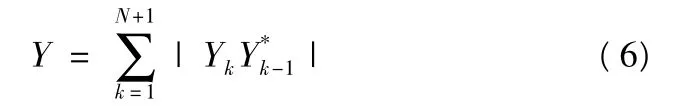
由于每组数据分为4 块,所以导航数据跳变位置为C 和D 的情况分别与跳变位置为B 位置和A 位置相同,这里不再赘述。
综上所述,结合并行码相位FFT 捕获方法,可以得到改进的弱信号捕获算法的具体流程图如图3 所示。
改进后的弱信号捕获算法具体流程如下:
1)读入N×20 ms 卫星信号数据,在当前搜索的频点上进行中频信号与载波的混频。
2)将读入的数据以20 ms 为单位分组,每组再以5 ms为单位进行数据分块,分块形式见图2。
3)分别对每个5 ms 数据块进行数据累加,得到1 ms 的累加数据,并对累加后的1 ms 数据进行FFT 操作,与本地C/A码的共轭FFT 相乘,对相乘结果进行FFT 逆变换,这样便得到了4 ×N 组累加数据块的相干积分结果。分别每组数据相同位置的相干积分结果进行平方累加,得到4 组累加结果。
4)比较4 组累加结果,结果最小的一组对应的数据块位置中存在导航数据比特跳变。
5)以存在导航数据比特跳变的数据块为边界,将2 个边界之间的相邻3 组数据块的相干积分结果进行累加,得到相当于15 ms 的相干累加结果。
6)再对这些相干积分结果取模后进行差分累加,累加后的结果与门限值比较,若大于门限值则捕获成功,否则继续在下一频段搜索。
由以上分析可知,在改进的弱信号捕获方法中,导航数据跳变位置被更加精确地确定在了5 ms 的数据中,这样每20 ms 的数据便可以进行15 ms 的相干累加,结合差分累加,捕获的信噪比增益较传统半比特方法将大大提升。同时,采取先累加后相关的方法减小捕获过程中的计算量,算法的执行速度得以提升。
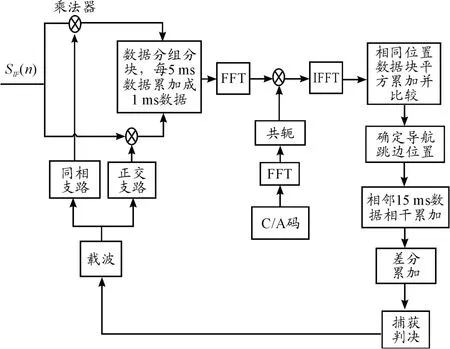
图3 改进的弱信号捕获算法流程
3 仿真分析
为了验证改进的弱信号捕获算法的有效性,在Matlab 环境下对弱信号捕获算法进行了仿真。设置仿真参数:采样频率: fs=8.184 MHz;中频频率: fi=4.309 MHz。采用恒虚警门限法,虚警率设为10-2。
首先对改进的弱信号捕获算法与传统的半比特方法在捕获概率上进行比较。每种方法读入100 ms 的卫星数据,分别在不同信噪比下进行信号捕获,每个信噪比下面进行100 次捕获,最终计算其捕获概率,得到的结果图如图4所示。

图4 改进算法与传统算法性能对比
由图4 可知,相比于传统的半比特方法,改进的弱信号捕获方法在捕获灵敏度提升上效果较好。在相同的捕获概率下,改进的算法比传统半比特算法灵敏度提高了2 ~3 dB。
在正常的室内弱信号环境下,GPS 信号的信噪比SNR 大约在-34 dB 左右,此时采用改进的弱信号捕获算法进行信号的捕获,使用100 ms 的卫星信号数据,结果如图5 所示。
由图5 可知,在正常的室内弱信号环境下,改进的捕获算法可以很好地捕获到卫星信号,捕获过程中噪声干扰小,在捕获点处相关值突出,捕获效果好。
为了验证改进捕获算法的捕获灵敏度,继续降低卫星信号的信噪比,卫星信号长度依旧为100 ms,当信噪比SNR 达到-40 dB 时,改进捕获算法的捕获效果图和传统算法的捕获效果图分别如图6 和图7 所示。

图5 SNR= -34 dB 100 ms 数据改进算法捕获图
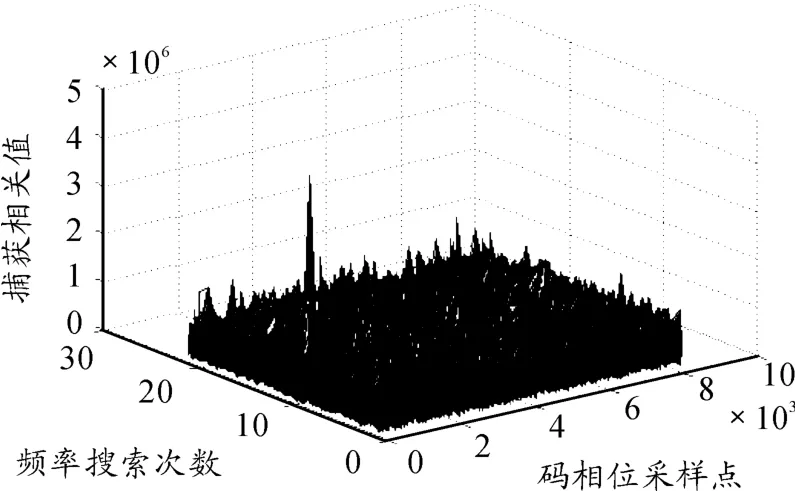
图6 SNR= -40 dB 改进算法捕获图
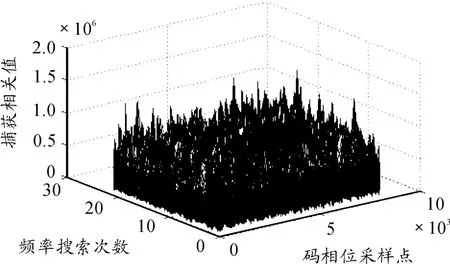
图7 SNR= -40 dB 传统算法捕获图
由图6 可知,当卫星信号的信噪比降低到-40 dB 时,改进的捕获算法依然能够捕获到卫星信号,但捕获过程中噪声干扰比较大,捕获点处相关值依然比较突出; 而由图7 可知传统算法在此信噪比下已经无法捕获到卫星信号。继续降低卫星信号的信噪比,改进捕获算法依然可以捕获到卫星信号,但噪声干扰变大,捕获效果变差,所以认为其捕获灵敏度可以达到-40 dB。
4 结论
本研究介绍了一种新的弱信号捕获算法,在半比特算法的基础上进行了改进,将相干积分时间提高到了15 ms,并采用了新的累加方法提高信噪比。通过仿真分析,本研究的弱信号捕获算法可以成功的捕获到相当于室内弱信号的信噪比-40 dB 的卫星信号,比传统的半比特捕获算法捕获灵敏度提高了2 ~3 dB,使GPS 软件接收机在弱信号环境下也能快速地实现信号的捕获。
[1]Oleksiy V Korniyenko,Mohammad S Sharawi.GPS software receiver implementations[J]. IEEE Potentials Magazine,2007 (26):42-46.
[2]方科.高动态扩频信号捕获的多普勒补偿[J].四川兵工学报,2013,34(7):122-124.
[3]Yang Liu,Tian Jin.Analysis and compare of weak GPS signal acquisition algorithms[C]//IET International Communication Conference on Wireless Mobile and Computing.Shanghai,China,2009.
[4]O’Driscoll C,Petovello M G,Lachapelle G. Software receiver strategies for the acquisition and re-acquisition of weak GPS signals[C]//Proceedings of National Technical Meeting.California,USA,2008.
[5]Mao Wei-Lung,Chen An-Bang.New code delay compensation algorithm for weak GPS signal acquisition[J].AEU-International Journal of Electronics and Communications,2009,63(8):665-677.
[6]李寅寅,徐晓苏,刘锡祥.基于半比特交替和FFT 组合的GPS 软件接收机弱信号捕获算法[J].中国惯性技术学报,2012,20(1):46-50.
[7]谢刚.GPS 原理与接收机设计[M].北京:电子工业出版社,2009.
[8]唐康华. GPS/MIMU 嵌入式组合导航关键技术研究[D].长沙:国防科技大学,2008.
[9]马若飞.GPS 弱信号捕获算法研究及其在软件接收机上的实现[D].哈尔滨:哈尔滨工业大学,2010.
[10]文立,刘建业,李荣冰.面向深组合导航技术的GPS 软件接收机捕获算法[J].弹箭与制导学报,2009,29(1):31-34.
