底盘测功机内部损耗功率补偿曲线的拟合
2015-07-01安相璧焦宇飞
郭 正,安相璧,焦宇飞,王 龙,王 虎
(1.军事交通学院军用车辆系,天津 300161; 2. 72641 部队,济南 250300)
底盘测功机是车辆动力性检测的常用检测设备,在进行驱动输出功率的测量时,由底盘测功机内部转动惯件(支撑轴承、联轴器、升速器等)存在的机械阻力造成的内阻消耗是测量误差的主要来源。为保证检测的准确性,应对该内部损耗功率进行补偿[1]。
底盘测功机内部机械阻力的大小主要由传动系的结构和制造工艺水平决定,一般为定值F,由生产厂家给出以便进行内部损耗功率的补偿。利用反拖法进行内部损耗功率补偿的具体方法是: ①使用加装在底盘测功机上的反拖电机将底盘测功机滚筒的表面线速度提至96 km/h 并进行滑行测试;②对滑行测试中规定的每段滚筒线速度间隔所耗时间进行记录;③计算每段线速度间隔中名义速度下的内部损耗功率;④根据计算结果进行“内部损耗功率-速度”补偿曲线的拟合,并根据拟合的曲线通过底盘测功机的控制系统进行补偿。
内部损耗功率的补偿曲线通常采用最小二乘法进行拟合,已有的研究未对补偿精度和适用性进行讨论。本研究为使补偿曲线可以更好地反映底盘测功机的内部损耗功率的变化过程,将从拟合精度及拟合曲线的延伸性两方面考虑,以选取最优的最小二乘拟合方法。
1 内部损耗功率数据的采集
1.1 底盘测功机反拖滑行测试
使用反拖电机反拖底盘测功机运转,至其滚筒表面线速度到达96 km/h 后,使底盘测功机空转滑行,对滑行过程中规定的名义速度下的速度间隔区间及相应耗时进行记录,数据如表1 所示。

表1 底盘测功机反拖滑行测试数据记录
1.2 内部损耗功率的计算方法
在底盘测功机进行反拖滑行测试时,其内部损耗功率可以表示为

式中:P 为底盘测功机内部损耗功率(W); F 为底盘测功机内部转动惯件的机械阻力(N);v 为滚筒表面线速度(m/s);DIW 为底盘测功机的转动部件的当量惯量(kg); dv/dt 为滚筒表面的减速度(m/s2)。
对式(1)进行积分可得

式中:v2、v1分别为速度间隔区间; Δti为相应速度间隔的滑行时间。
由于每段速度间隔的速度差值(v2-v1)为定值8 km/h,设速度间隔区间中的名义速度为vi,(v2+v1)即为2vi,则名义速度点下的内部损耗功率P(vi)可表示为

将式(3)中的变量换算为本测试中所采用的单位(即功率的单位为kW,速度的单位为km/h),则式(3)可表示为

可以计算出如表2 所示的底盘测功机运行速率计算值。

表2 底盘测功机运行速率计算值
2 内部损耗功率曲线的拟合
为了完成控制系统对底盘测功机内部损耗功率的补偿,需要根据底盘测功机反拖滑行测试所得的数据结果,进行底盘测功机“损失功率——速度曲线”的拟合。拟合一般采用最小二乘的方法。所谓最小二乘法,是一种经典的数据拟合方法,通过最小化误差的平方和以寻找数据的最佳函数匹配。用此方法拟合P(vi)后,可对应每一速度点求出其内部损耗功率大小[2-3]。
以10 个名义速度点的数据作为拟合的原始数据,用最小二乘法结合Matlab 软件拟合P(vi)曲线,拟合曲线的次数分别为1 ~5 次,选取其中最理想的曲线参数作为拟合参数。图1、图2 分别为根据表1 所示数据所拟合得到的“损失功率——速度曲线”。
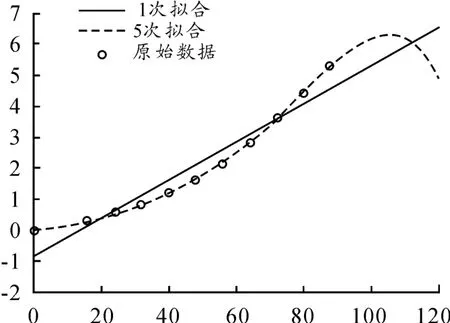
图1 1 次、5 次拟合曲线

图2 2 次、3 次、4 次拟合曲线
从图1 可以看出,1 次拟合曲线为一条直线,无法准确地反映反拖滑行试验的数据结果;而5 次拟合曲线在速度值达到100 左右时,就出现拐点,与实际不相符,因此1 次拟合及5 次拟合曲线均不能作为P(vi)的曲线。而2 次、3 次和4 次拟合曲线在速度值小于120 的范围内均不会出现拐点[4],且曲线都可较为准确地反映反托滑行试验的数据结果,可作为P(vi)曲线。
根据底盘测功机操作规范,测量时最低测试点车速必须大于直接档最低稳定车速的2 倍以上,最高测试点车速应小于车辆标称最高车速的4/5[5-8]。为了提高补偿曲线适用性,下面进一步分析这3 种拟合的精度和曲线延伸性,从中选择最优的曲线作为P(vi)曲线。将2 次、3 次、4 次的拟合曲线分别向正向(速度值大于100)进行延伸,得到如图3 所示的延伸曲线。

图3 正向延伸曲线
从图3 可以看出,当速度值超过120 后,4 次拟合曲线在速度为130 左右时会出现拐点继而下滑,即代表内部损耗功率下降,与实际情况是不相符的,由此得出,4 次拟合曲线的正向延伸效果较差,而2 次、3 次拟合曲线的正向延伸效果则较好。
衡量最小二乘拟合法精度的参数通常为相关系数和剩余平方和,相关系数的值越高、剩余平方和的值越小,则拟合曲线的精度则越高。为此,分别对2 次、3 次、4 次的拟合曲线的相关系数及剩余平方和进行计算,其结果如表3 所示。从表3 中可以看出,3 种拟合方法得到的拟合曲线的精度都比较高,相对而言,4 次拟合曲线的精度最好,3 次拟合次之,2 次拟合效果最差。

表3 拟合曲线的相关系数及剩余平方和
根据以上的分析,可以看出:5 种拟合的方法得出的“损失功率——速度曲线”中,1 次拟合及5 次拟合曲线与实际情况严重不符,2 次拟合曲线的延伸性较好但精度一般,4 次拟合曲线的精度高但延伸性较差,而3 次拟合曲线无论是精度还是延伸性都较好,更加适用于对底盘测功机内部损耗功率的补偿。
3 结论
为了补偿底盘测功机的内部损耗功率,本研究在进行底盘测功机反拖滑行试验的基础上,根据试验所得结果,采用最小二乘的方法,对所需的“内部损耗功率-速度”补偿曲线分别进行1 次到5 次的拟合,通过对其拟合精度和拟合延伸性的分析,得出:采用最小二乘的3 次拟合法拟合出的“内部损耗功率-速度”补偿曲线更为准确。
[1]安相璧.汽车检测诊断技术[M].2 版.北京:北京理工大学出版社,2009.
[2]JT/T445—2008,底盘测功机[S].
[3]董改花.零秒电阻最小二乘曲线拟合函数选择的探讨[J].微电机,2012(11):75-77.
[4]刘平.基于测功机的汽车动力性评价误差分析[J].公路与汽运,2003,2(4):8-9.
[5]李大伟. 多轴驱动车辆底盘测功机系统研究与仿真[D].天津:军事交通学院,2011.
[6]王娜.HYCG-10A 型底盘测功机测试性能改进[D].哈尔滨:哈尔滨工程大学,2007.
[7]李世伟.汽车底盘测功机测控系统的设计与实现[D].西安:西北工业大学2003.
[8]赵鑫.汽车动力性台架试验及评价方法研究[D].西安:长安大学,2012.
