船舶阻力换算中形状因子的计算研究

江 杰，李彦强

(海军装备技术研究所动力技术研究室，北京 102400)

船模阻力试验换算方法最早由傅汝德提出，该方法将船体总阻力分成摩擦阻力Rf和剩余阻力Rr，并认为摩擦阻力仅与雷诺数Re 有关，剩余阻力仅与傅汝德数Fr 有关，且两者互不干扰。在此基础上，休斯提出了三因次换算方法，引入形状因子1 +k 来表达船体粘性阻力和相当平板摩擦阻力之间的关系。引入形状因子的三因次法较二因次法合理，其中形状因子可由低速拖曳或叠模试验确定。目前，三因次换算方法被广泛应用于各大水池阻力试验中，但是休斯提出的1 +k 为常数的假定是否正确有待进一步探讨［1］。

有关尺度效应的试验研究有几何相似船模组试验，通过几何相似船模组试验不仅可以比较不同换算方法的合理性，还能分析形状因子及推进效率中各种成分的尺度效应等问题。但是船模试验往往受到各种限制，几何相似船模组试验亦不能给出实船雷诺数下的信息。随着现代船舶流体力学的发展，有关船模实船阻力换算中尺度效应的计算和验证方面的研究不断增多。欧洲几大水池合作的VIRTUE［2］，EFFORT 等项目均包含实船数据测量及全尺度外推技术和尺度效应相关的研究。Raven［3］等对HTC 船模进行了模型和实尺雷诺数下的数值计算，计算结果表明实尺雷诺数下形状因子比模型雷诺数下大7%。倪崇本［4］采用k -ε 湍流模型计算了S60 船模在傅汝德数在0.1 到0.2 各航速下形状因子，计算结果表明形状因子1 +k 随航速的增加而增大。

船模实船阻力换算常常通过低速时船模阻力数据或者低速时叠模计算来求得船体的形状因子。但是本文计算表明雷诺数及航行姿态对某些船型的形状因子产生显著的影响，若采用正浮姿态下船模尺度的叠模计算求取形状因子将导致较大的误差。本文基于数值计算比较了航速，姿态，实船雷诺数对DTMB5415 及KCS 船模形状因子的影响。计算表明:对DTMB5415 船型，考虑航速、姿态、实船雷诺数的影响，在Fr=0.41 时实船雷诺数下的形状因子比Fr=0.1 模型雷诺数下形状因子大44%。对KCS 船型，考虑航速，实船雷诺数的影响，其在Fr =0.271 下实船形状因子比其在Fr =0.086 下船模形状因子大7%。基于低速下叠模计算或者拖曳试验得到的形状因子必然导致换算得到的实船阻力产生较大的误差。

1 数值计算基础理论

1.1 控制方程及计算模型

采用有限体积法离散控制方程，不可压缩粘性流体的控制方程如下:

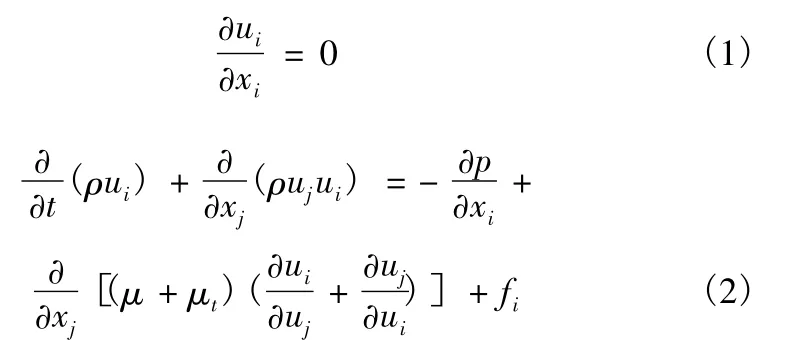
式(1)、(2)分别为连续性方程和动量方程。ui分别为流体质点在i 方向的速度分量，fi是质量力;p 为流体的压力;μ 是相体积分数平均的动力黏度系数;μt为湍流动力黏性系数。

上述方程需要结合湍流模型封闭方程组，常见的两方程湍流模型有k-ε、RNG k-ε、k-ω、SST k-ω、RSM 等。由于船体绕流带有复杂的分离，伴流现象，而湍流模式对准确预报伴流及流动分离有重要的作用。本文参考文献［5］，选用SST k-ω 湍流模型，基本方程参考文献［6］。

SST k-ω 湍流模型集合了k -ε 模型和k -ω 模型的优点:在近壁面区域，采用k -ω 模型，湍流耗散较小，收敛性好;在湍流充分发展的区域，采用k -ε 模型数值模拟，计算效率高。SST k-ω 湍流模型对壁面和尾流场模拟效果好，对自由来流的湍流度不敏感［7］，具有较好的稳定性。

1.2 船舶阻力换算方法

船模阻力试验换算方法最早由傅汝德提出，该方法将船体总阻力分成摩擦阻力Rf 和剩余阻力Rr，并认为摩擦阻力仅与雷诺数Rn 有关，剩余阻力仅与傅汝德数Fn 有关，且两者互不干扰［1］。因此总阻力系数可以表示为

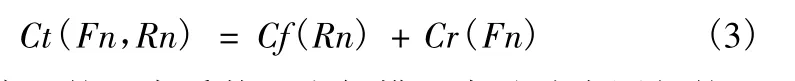
因此实船尺度下的阻力系数可由船模阻力试验中测得的阻力系数表示为

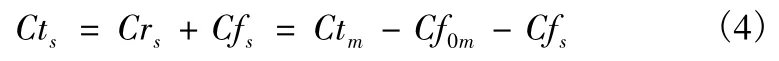
其中Cf0代表相当平板摩擦阻力系数，Cr 为剩余阻力系数，下标s 和m 分别代表变量对应于实船和模型。在此基础上，休斯提出了三因次换算方法，引入形状因子1 +k 来表达船体粘性阻力和相当平板摩擦阻力之间的关系:

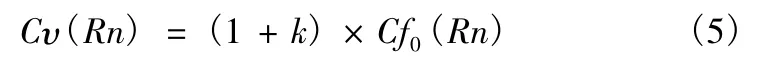
此时有

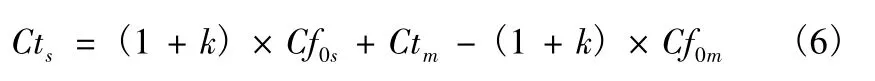
引入形状因子的三因次法较二因次法合理，其中形状因子可由低速拖曳或叠模试验确定。考虑到实船船体表面粗糙度的作用以及船模实船阻力换算过程中由于雷诺数不相等导致的尺度效应，需要补贴一定的经验系数，即船模实船换算补贴Ca，Ca可由式(7)确定:

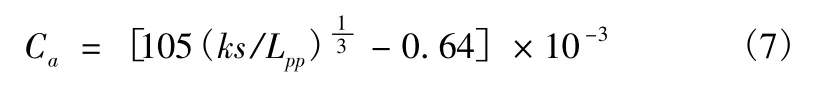
Lpp为垂线间长，ks 为粗糙度表观高度，一般可取ks=0.15mm。

2 数值计算及分析

2.1 DTMB5415 船型数值计算

DTMB5415 是ITTC 推荐的军舰类型中唯一有大量公开试验数据的研究对象(图1)。美国的DTMB，IIHR 以及意大利的INSEAN 三家研究机构对该船型进行了全面的试验。DTMB 5415 船模缩尺比为λ=24.8，其实船与船模的主要数据如表1 所示。

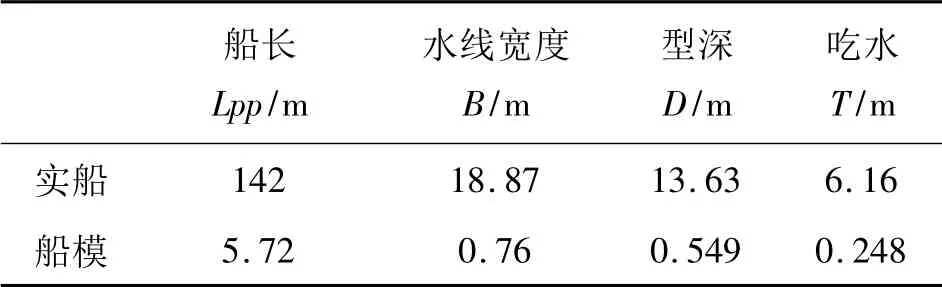
表1 DTMB5415 船体几何尺寸

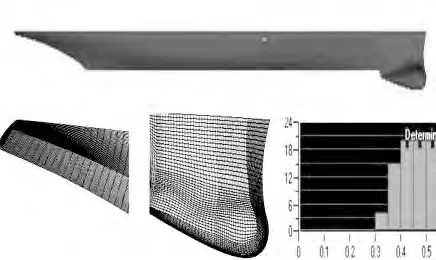
图1 DTMB5415 叠模模型几何，表面网格及网格质量

在实际船模试验时，通常忽略低航速下船舶的兴波阻力，采用傅汝德数低于0.15 的船模试验数据来计算船模的形状因子。但是低航速下流动不稳定，导致测量阻力也不稳定。本文采用叠模计算可以在较大的范围内求取船舶的粘压阻力及形状因子。叠模模型尺寸与相关模型试验一致，以船模中纵剖面与静水面为对称面。数值计算区域计算区域入口取船艏向前延伸1 倍船长处，出口取船艉向后延伸2 倍船长处，侧边界及下方边界均取1 倍船长。

2.1.1 模型雷诺数下形状因子随航速变化

鉴于船模试验通常采用傅汝德数低于0.15 的船模阻力数据来计算形状因子，本文首先计算了傅汝德数0.1 ～0.15各航速下的粘压阻力系数及形状因子。然后计算了傅汝德数在0.28，0.36，0.41 下船模的形状因子，以此分析粘压阻力系数及形状因子在较大航速范围内变化规律。为表示粘压阻力系数与摩擦阻力系数变化的关系，定义k1为粘压阻力与摩擦阻力的比值。表2 列出了Fr 从0.1 ～0.41 航速范围内粘压阻力系数，形状因子1 +k 及k1的变化。

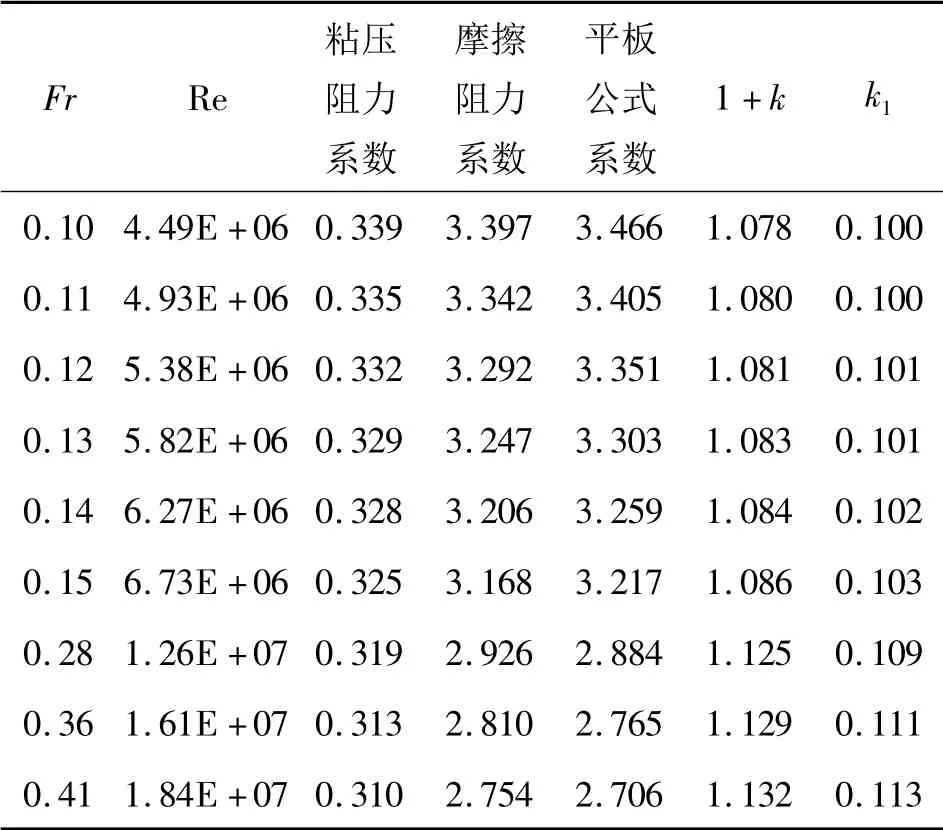
表2 不同航速下形状因子的变化

从表1 可以看出，随着航速增加(即雷诺数增大)，粘压阻力系数下降，但是粘压阻力系数相对于摩擦阻力系数不断增大，即k1和形状因子增大。当Fr 从0.1 增加到0.41 时，k1增大了13%。在较低的航速范围内，形状因子变化不大，Fr 从0.1 ～0.15 航速范围内，形状因子增大了0.7%。但是Fr 由0.1 增大到0.41，1 +k 值增大了5%。因此若采用低航速下计算得到的形状因子来外推实船在高航速时的阻力，导致粘性阻力低估5%。

2.1.2 模型雷诺数下形状因子随姿态的变化

当船舶航速较大时，船体的姿态对阻力产生显著的影响，此时主要体现在湿表面积及各项阻力系数的变化。考虑船体姿态变化，针对不同航速下姿态分别进行建模与网格划分，此时叠模模型为该航速下首尾吃水的连线以下的船体部分。鉴于低航速下船模姿态变化较小，对阻力的影响可以忽略不计，本文仅计算Fr 大于0.28 的3 个航速。不同航速下船体姿态如表3，不同姿态下形状因子的变化如表4。

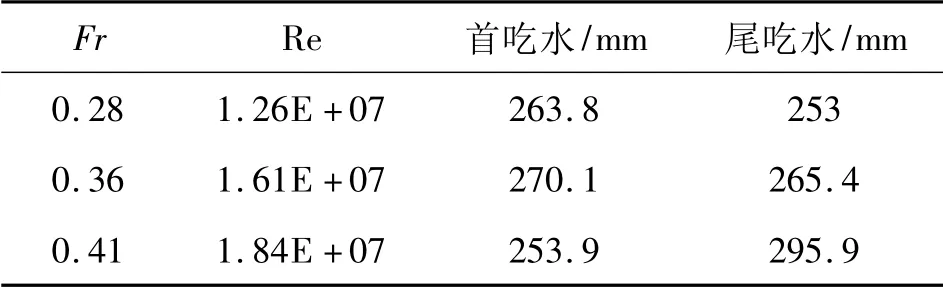
表3 不同航速下船模的航行姿态

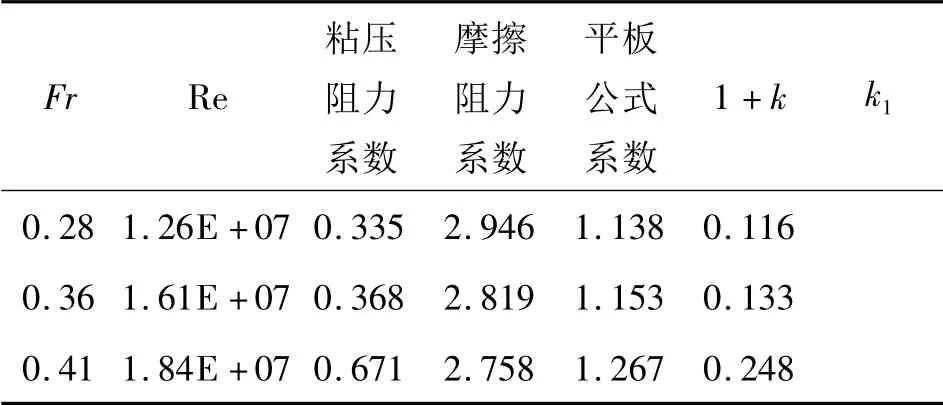
表4 不同姿态下形状因子的变化

计算表明，考虑船体吃水和纵倾变化之后，湿表面积增大，摩擦阻力增大，但是由于雷诺数不变，摩擦阻力系数不变。在较高航速下船模产生较大的平行下沉及纵倾，粘压阻力系数及形状因子k 增大，3 个航速下形状因子分别增大了1%，2%，12%。Fr=0.28 和0.36 时，船体姿态变化不大，粘压阻力系数变化不明显;当Fr =0.41 时，船体姿态变化较大，粘压阻力系数增大了117%。

2.1.3 实船雷诺数下形状因子随航速变化

不考虑船体姿态，实船雷诺数下的粘压阻力系数及形状因子变化如表5。

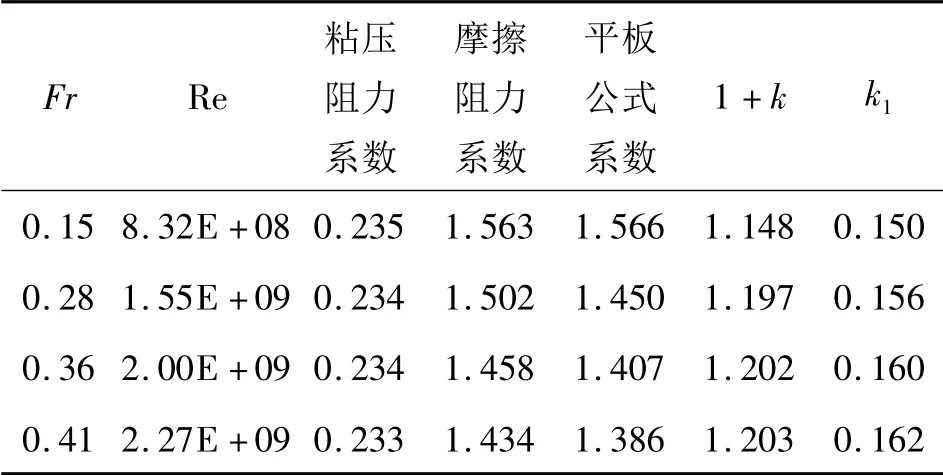
表5 不考虑姿态实船雷诺数下形状因子的变化

在实船雷诺数下，随着航速的增大，粘压阻力系数略微减小，摩擦阻力系数不断降低，故形状因子增大。实尺雷诺数的形状因子要比模型雷诺数下形状因子分别大5.7%，6.4%，6.4%，6.2%。

考虑船体姿态，实船雷诺数下粘压阻力系数及形状因子在各航速变化如表6。考虑船体姿态变化和实船雷诺数的影响之后，船舶的形状因子变化比较明显。其中在Fr 为0.41时，形状因子较该航速模型雷诺数下不考虑姿态计算值增加了37%，较Fr=0.1 模型雷诺数下形状因子计算值增加了44%。若按照形状因子为一常数的假定，采用低速正浮下叠模计算得到的形状因子来外推高航速的粘性阻力时，将会导致粘性阻力低估44%(表6)。

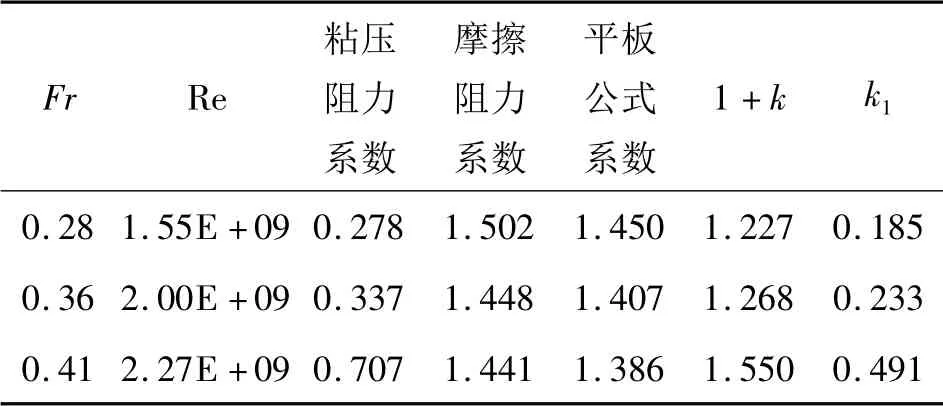
表6 考虑姿态实船雷诺数下形状因子的变化

2.2 KCS 船模计算

KCS 作为国际船舶操纵性比较研究的货船船型，其各种试验数据在Gothenburg 2000 会议资料中公布，表7 给出了其主要尺寸。本文对KCS 进行叠模计算的叠模模型均未考虑各航速下船体姿态的变化(图2)。

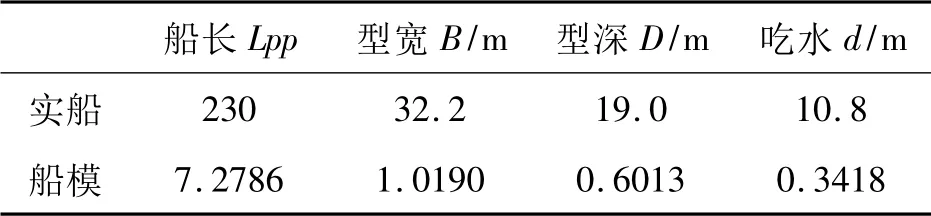
表7 KCS 船体几何尺寸

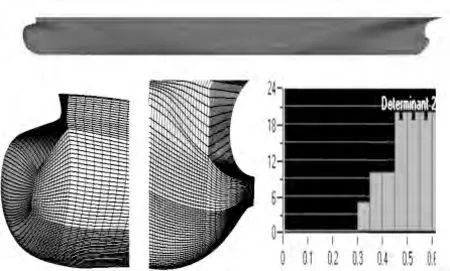
图2 KCS 叠模模型几何，表面网格及网格质量

2.2.1 模型雷诺数下形状因子随航速变化

模型雷诺数下KCS 形状因子随航速变化如下。

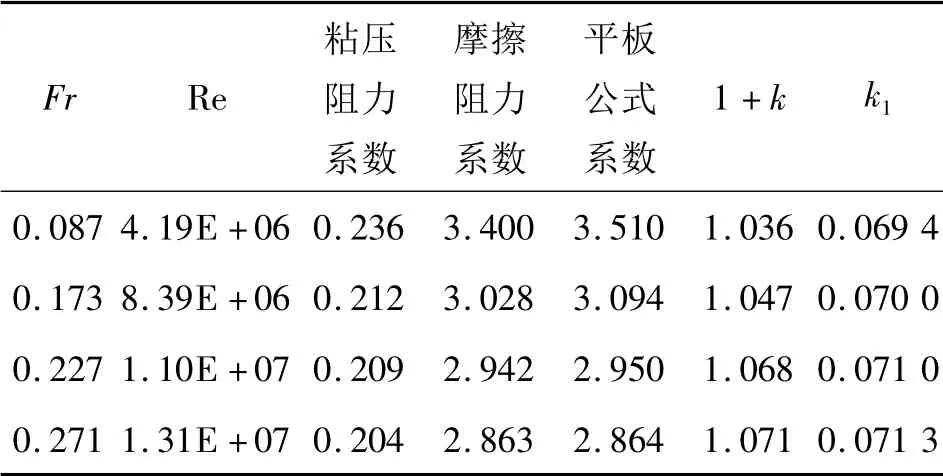
表8 不同航速下形状因子的变化

从表8 可以看出，Fr 从0.087 增大到0.271，粘压阻力系数与摩擦阻力系数下降，形状因子增大了3. 4%，k1增大了6%。

2.2.2 实船雷诺数下形状因子随航速变化

实船雷诺数下KCS 随航速变化如下(表9)。

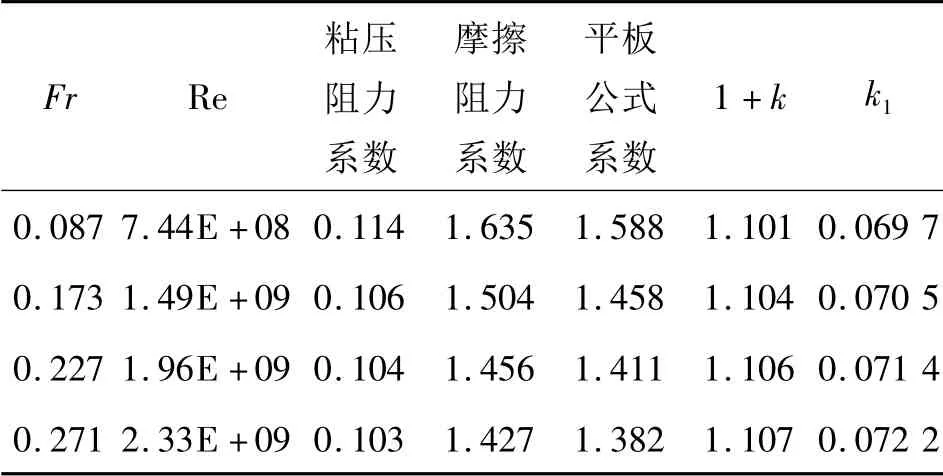
表9 不考虑姿态实船雷诺数下形状因子的变化

实船雷诺数下，形状因子随航速变化较小，在Fr 从0.087 到0.271 的航速范围内，形状因子变化不超过0.5%，k1随航速变化不超过3.5%。相比模型雷诺数下叠模计算值，形状因子分别增大了6.3%，5.4%，3.6%，3.4%，k1的变化不超过1.3%。

从上述计算可以看出，KCS 在Fr =0.271 时实船雷诺数下形状因子比Fr=0.087 模型雷诺数下形状因子大7%，若采用模型雷诺数下低航速叠模计算得到形状因子会产生较大误差。KCS 的形状因子变化没有5415 形状因子变化大，主要原因可能是:其最高航速较小且未考虑航行姿态的变化，水线以下线型较为光顺，流动分离较少。

3 结论

1)本文通过对DTMB 5415 和KCS 的叠模计算证明了船舶的形状因子并不是一个常数，航速，航行姿态及实船雷诺数均对形状因子产生显著的影响。

2)考虑航速、姿态、实船雷诺数的影响，DTMB 5415 在Fr=0.41 时实船雷诺数下的形状因子比Fr =0.1 模型雷诺数下形状因子大44%。若采用低速正浮叠模计算得到形状因子进行换算来求取实船高速时的阻力将导致明显的误差。

3)对KCS 船型而言，航速及实船雷诺数的影响使形状因子变化了7%。

现有的船模实船换算方法之所以没有产生明显的误差，主要是采用低速拖曳试验得到的阻力中含有一定的兴波阻力成分，此时得到的形状因子较叠模计算值偏大。且换算过程中结合船模实船换算补贴，使其在一定航速范围内具有较高的精度。为精确预报实船在较高航速的阻力，必须要考虑形状因子的变化，此时形状因子可以通过数值计算或者试验来求取。

［1］盛振邦，刘应中.船舶原理［M］.上海:上海交通大学出版社，2003.

［2］李胜忠，李斌，赵峰，李力枫.VIRTUE 计划研究进展综述［J］.船舶力学.2009:13(4).

［3］Raven H C，van der Ploeg A，Starke A R，et al.Towards a CFD-based prediction of ship performance-Progress in predicting full-scale resistance and scale effects［J］. International Journal of Maritime Engineering，Transactions RINA，2009，150(3):54-57.

［4］倪崇本，朱仁传，繆国平，等.一种基于CFD 的船舶总阻力预报方法［J］.水动力学研究与进展(A 辑)，2010，25(5):579-586.

［5］张志荣，赵峰，李百奇.k -ω 湍流模式在船舶粘性流场计算中的应用［J］.船舶力学，2003，7(1):33-37.

［6］STERN F.Final report and recommendations of the resistance committee［C］//Proceedings of 23rd international towing tank conference. Seoul/Shanghai: ITTC，2002，173-246.

［7］Menter F R.Two-equation Eddy-viscosity turbulence models for engineering applications［J］.AIAA Journal，1994(32):1598-1605.