初始段大离轴制导律研究
2015-07-01郭晓楠罗绪涛
郭晓楠,徐 挺,罗绪涛,王 霞
(中国空空导弹研究院,洛阳 471099)
第四代近距格斗导弹要求具有大离轴发射能力,在大离轴角初始飞行段,导弹的制导控制指令应当完成导弹的快速转弯,快速消除弹道初始误差,从而进入稳定的末制导阶段。常用的比例导引律弹道比较平直,而且工程上实现容易,因此在空空、地空导弹上得到了广泛的应用。然而,比例导引律以消除视线角速度为主,不以减少离轴角为主要目的,并不能满足大离轴角制导阶段制导需求。本文针对大离轴角发射初始段需求,快速实现速度矢量对准预测拦截点,以弹道收敛和离轴角减小为目标进行制导律设计,并根据制导信息情况适当简化制导律准则,考虑导引头和惯性测量单元所能得到的信息源形成实用性强的简化制导律。
1 平面拦截数学模型
导弹-目标平面拦截几何关系见图1,图中R 代表导弹-目标间的相对距离,q 代表导弹-目标间的视线角,为视线角速度,Vm代表导弹速度,θm为弹道倾角,Vt、θt为目标速度及速度方向角。
由图1 可以得到导弹-目标间的非线性运动学关系描述为

其中:ηm=q -θm为导弹前置角;ηt=q -θt为目标前置角;为导弹的横向加速度;为目标的横向加速度为导弹的纵向加速度为目标的纵向加速度。导弹前置角还可表示为导弹离轴角φ 和攻角α 的关系,即ηm=φ+α。考虑初始发射时,α=0,则ηm=φ。

图1 平面拦截几何关系
2 大离轴发射制导约束条件

因此

变换得到

即

令导弹制导指令ac=amcos(q-θm),则对于导弹前视攻击情况(初始离轴角小于90°),对任意目标进入角如果式(6)成立,则,弹道收敛。

显然,只有当导弹横向加速度指令足够大时,式(6)才可以得到满足。这说明导弹横向加速度很大时对任意目标进入角和导弹前视攻击情况,能够保证弹道收敛。因此,在较大离轴角情况下,采用足够大的横向控制过载应能保证弹道收敛,这也可以部分说明为什么AIM -9X 等新一代格斗导弹的最大可用过载往往在60 以上。
3 初始段大离轴制导律
大离轴制导段,以消除大离轴角为主要目标,即保证θm→q,使得相对速度尽快进入收敛状态。为此,在制导律设计中取李雅普洛夫函数为

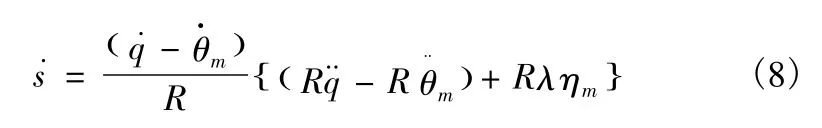
考虑到

则
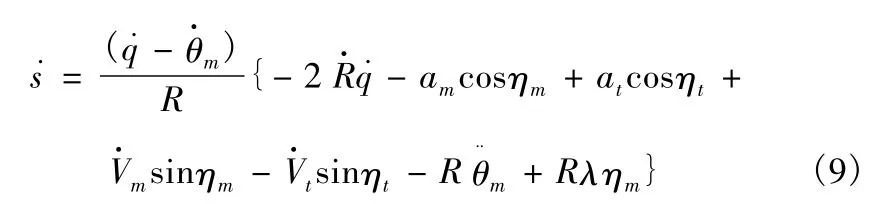
设导弹自动驾驶仪/弹体模型为一阶动态环节,传递函数为

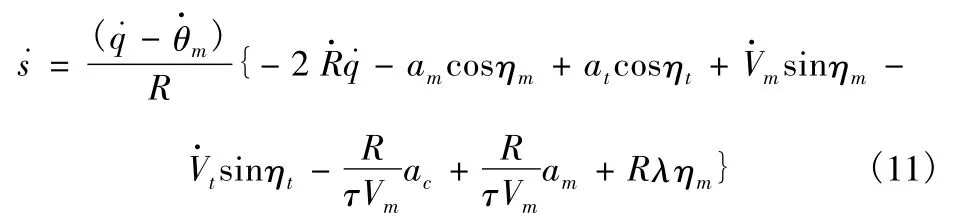
在式(11)中令

变换得到

而


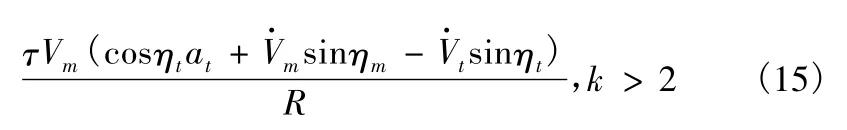
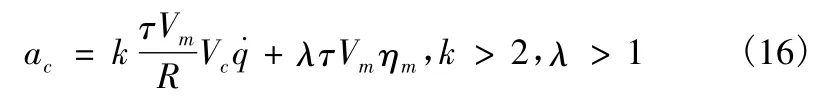
由式(16)可以看出,该制导律是在比例导引律的基础上引入了和导弹前置角成比例的补偿项,用于消除初始段的离轴角,是适用于大离轴发射的制导律。考虑比例导引的通用形式,可将式(16)进一步简化成如下形式,即比例导引+变系数追踪导引
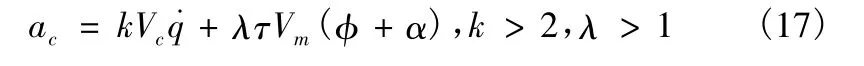
4 数字仿真
在Matlab 环境下建立某空空导弹制导系统平面仿真模型。其中导引头为简化一阶模型,时间常数0.03 s,驾驶仪为等效二阶模型,时间常数0.1 s,阻尼0.6,并设定脱靶量小于1 m 为制导精度合格判据。
制导律参数选取形式如下:
制导律1:比例导引律ac=kVc,k=5。
制导律2:比例导引+ 变系数追踪导引ac= kVc+λτVm(φ+α),k=5,λ=3,τ=0.1。
仿真初始条件为6 km 高度迎头攻击,导弹、目标初速0.8 M,在固定发射离轴角条件下比较两种制导律的攻击近界。仿真结果如表1,图2 ~图4 为发射离轴角75°典型条件下两种制导律对应的弹目相对运动轨迹、加速度指令及离轴角曲线。
由仿真结果可以看出,制导律2 在大离轴发射情况下较制导律1 更快消除离轴角,有更小的转弯半径和攻击近界。通过仿真,验证了大离轴制导律的攻击效果。

表1 不同制导律大离轴发射攻击近界
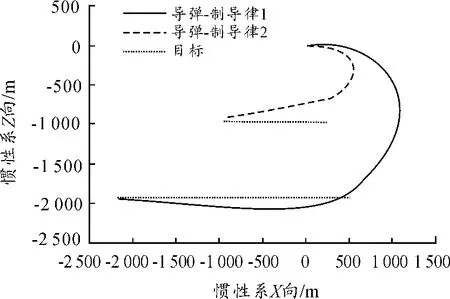
图2 水平面弹目相对运动轨迹

图3 加速度指令
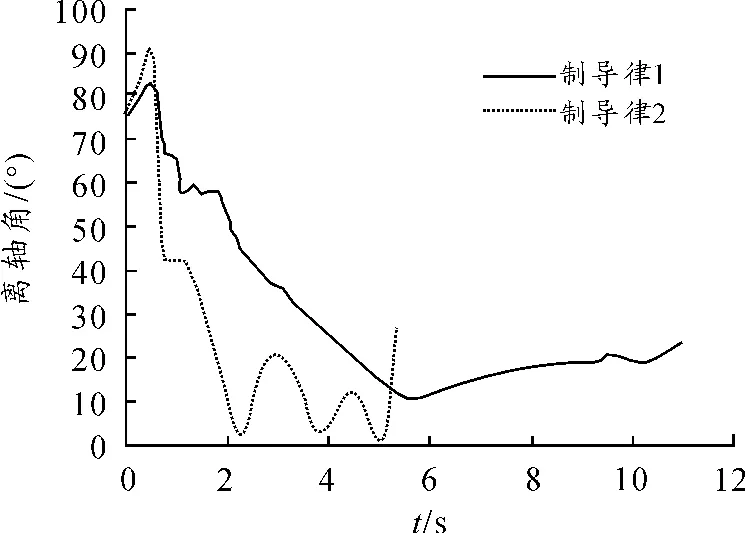
图4 离轴角
5 结论
本文在理论分析大离轴发射制导需求的基础上,利用李雅普洛夫分析方法,零化离轴角进行制导律的推导,并考虑导引头和惯性测量单元所能得到的信息源形成实用性强的简化制导律,即比例导引+变系数追踪制导律。并通过数字仿真,证明大离轴制导律在大离轴发射情况下较比例导引更具优势。
[1]徐挺,李斐,王霞.制导系统精度分析及误差分配方法[J].四川兵工学报,2014(3):18-20.
[2]唐成师,侯明善.发射后截获制导律研究[J].火力与指挥控制,2013(2):55-58.
[3]李斐,徐挺,王霞.基于大离轴制导律的一段式越肩发射制导模式[J].弹箭与制导学报,2014(3):53-55.
[4]王锡泉,黄惠晶.空空导弹大离轴发射条件下的控制研究[J].战术导弹控制技术,2006(4):10-12.
[5]李友年,王霞.无数据链情况下红外空空导弹射后截获概率研究[J].四川兵工学报,2013(10):4-7.
[6]刘巩,罗绪涛.大离轴发射空空导弹初制导律[J].四川兵工学报,2010(3):31-33.
[7]何素娟,周凤岐.敏捷导弹大角度姿态控制系统设计(英文)[J].系统仿真学报,2011(5):906-910.
[8]李毅,王锡泉.大离轴发射条件下空空导弹快速转弯制导律研究[J].弹箭与制导学报,2008(4):15-18.
