Fluent在碟形深潜器水动力性能的应用分析

王金强++王平平++母宝颖

摘 要：文章利用Fluent方法模拟了一种新型碟形深潜器在直航状态所受的总阻力以及斜航状态下所受的横向力Y和纵向力X并与试验方法进行比较从而得出Fluent模拟方法具有一定的准确性可以应用于该碟形潜器的水动力性能分析。碟形深潜器水动力性能的预报对于其外形的优化至关重要，传统的研究方法主要有有理论方法、试验方法和数值模拟。众所周知，试验方法一直是碟形潜器研究的主要方法，而随着计算机技术的快速发展，以流体力学为基础的计算流体力学方法也逐渐成为一种重要方法，与传统方法相比，运用Fluent模拟的方法则更加灵活和经济，但该方法与试验方法的相对误差随着Fr数的增加而增加，进而说明该方法还需要进一步优化。

关键词：碟形深潜器；水动力；数值计算；CFD；Fluent

中图分类号：TV131 文献标识码：A 文章编号：1672-3791（2015）05（c）-0000-00

本文将首次利用这一先进技术对该新型碟形潜器的阻力性能进行初步的数值计算分析，并与理论计算结果相比较证明使用Fluent技术得到的模拟结果是可信的.通过比较计算结果和模拟试验结果之间存在偏差为此提出了下一步工作内容。

1 控制方程和湍流模型

1.1基本的控制方程

文中模拟以上图1的三维模型在静水中以定常速度U0作匀速直线运动时船体周围的粘性流场. 根据相对运动原理可视作船体模型静止而水以速度-U0从远方相对于潜器模型匀速流动. 假定流

体是不可压的则流场的连续方程和动量方程分别为：

（1） （2）

式中： ， 为速度分量时均值（i，j =1 2 3 ）；P为压力时均值；ρ为流体密度；ν为流体粘性系数； 为重力加速度分量； 为雷诺应力项. 方程中的雷诺应力项属于新的未知量.因此要使方程封闭必须对该应力项作某种假设即建立应力的表达式通过表达式或湍流模型把应力项中的脉动值与时均值联系起来.文中选取理论上发展较为完善 在工程上广泛运用的a -E二方程湍流模型来封闭RANS 方程.湍流模型的方程如下：

式中：C1 =1.44 C2 =1.92 =1.0 =1.3.

通过湍流运动粘度Vt建立了Reynolds应力与平均速度梯度的关系 使得控制方程封闭.Vt表示成k和 的函数 即：Vt= .

为经验常数 =0.09.

1.2湍流模型

本文主要应用了RNG k一 占模型，因为模拟弯曲壁面流动的时候，标准k—s模型会失真，则没有选择标准模型，其相应的湍流输运控制方程如下：

RNG k一占模型，湍流方程如下：

其中 是湍动粘度， ， 是经验常数， 是湍动耗散率，

是湍动能，Gk是因均速梯度引起的湍动能的产生项， 是主流的时均应变率。

2.数值模型及网格划分

以用于水池实验的潜器模型为原型并按1：1利建立用于计算的模型. 模型总长度为1.025m 最大宽度为0.65m. 为了更好地保证计算域的对称减小误差本文采取矩形域，在进行潜器表面和计算域网格划分时，由于潜器表面型线很复杂，在对网格相关参数设置时采取在近潜器区域设定较密的网格然后以一定膨胀系数外推的方式，同时采用结构化网格和非结构化网格混合划分的方式，这样一方面能够合理地减少网格数目另一方面也能较准确地捕捉到近潜器区域的流动特性. 为此文中采用网格自适应技术在计算过程中让求解器自动判断并进行网格优化以此达到捕捉流场形状的目的，从而提高数值计算的效率。生成的混合结构网格模型如下图1所示；

3.计算结果和分析

3.1潜器直航计算

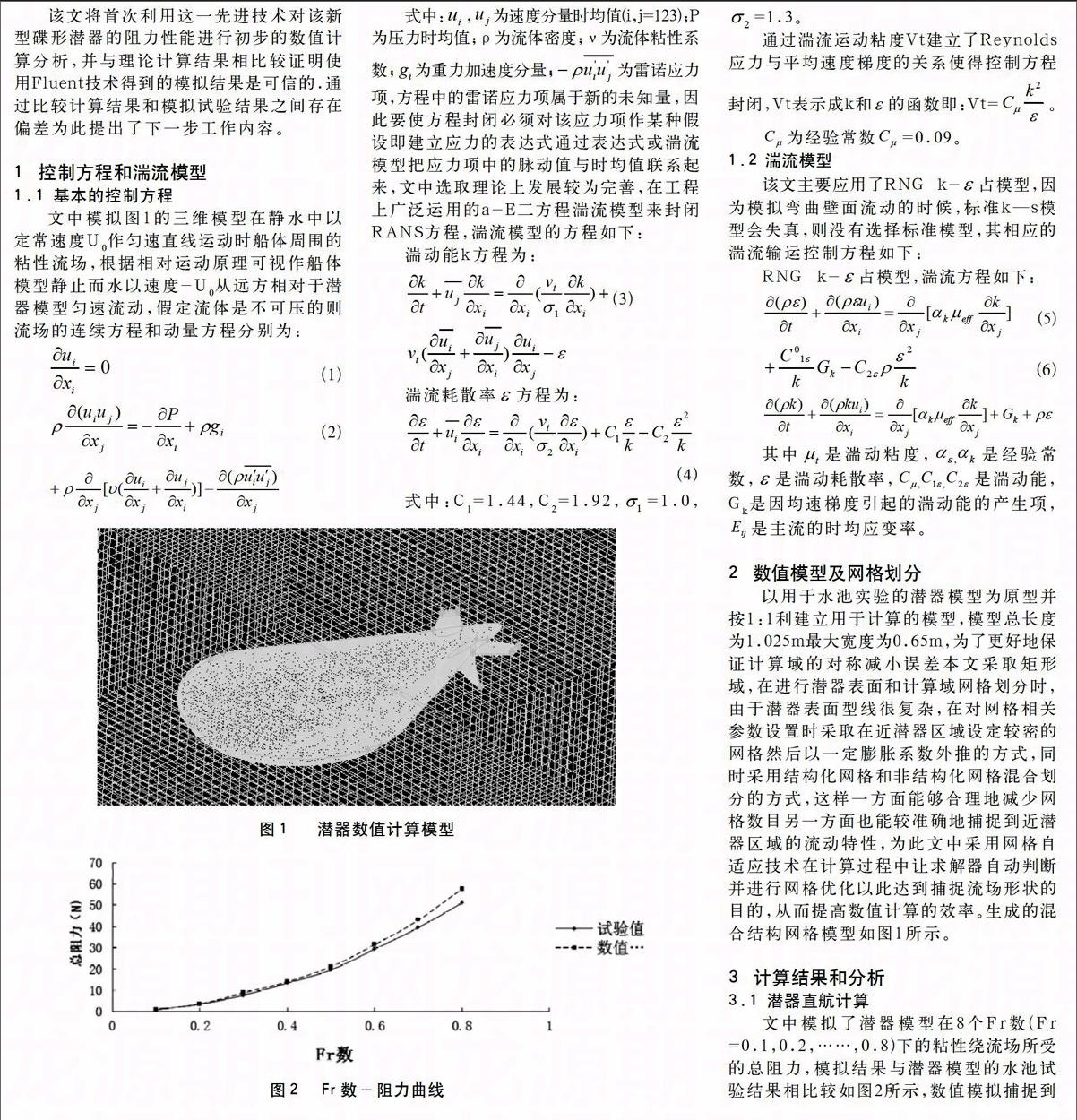
文中模拟了潜器模型在8个Fr数（Fr =0.1，0.2，……，0.8）下的粘性绕流场所受的总阻力，模拟结果与潜器模型的水池试验结果相比较如图2所示，数值模拟捕捉到的潜器周围流体的速度云图如图3所示，潜器表面的压力分布云图如图4所示.

由Fr数-阻力曲线可以看出文中计算所 得的阻力曲线和试验方法所得曲线发展趋势基本上一致，基本能较好地反映潜器在水中的运动情况且阻力曲线来看各个Fr 数下的阻力值与试验结果相比均没有太大的偏差相对误差均在7%以下，故整个计算过程是稳定可信的。

（1）由速度云图可以明显看出，对于粘性流体绕流会在潜器的最前端点处产生边界层，在边界层的内部，速度会随着距船体表面距离增大而增大。由于边界层的作用，主流的流线不是像理想流体时绕潜器流动，在到达潜器尾部最后端点处形成驻点，而是被外推，流线上的点在潜器尾部处的速度不是零，这与实际情况是吻合的。

（2）由压力分布云图可以看出潜器前端的压力最大，背部的压力最小，首部的压力明显大于尾部的压力这与潜器采用NACA翼型剖面是符合的。

3.2潜器斜航模拟计算

所谓的斜航模拟就是将潜器与其纵中剖面成一夹角， 给定水流速度， 当漂角为小量时有

且fluent设置唯一与直航不同是水平面斜航时多了一个纵向的速度， 垂直面斜航时多了一个垂向的速度。垂直面攻角α和水平面漂角β变化范围都是从 ，间隔 ，不同垂向速度的来流，在Fr=0.2和Fr=0.4时所受横向力Y与漂角α和纵向力X与攻角β的受力关系，通过数值计算所得的潜器斜航时所受横向力与纵向力与试验所测结果的相对误差允许范围内，说明数值 计算结果具有可信性。

4结论

1）Fluent模拟方法计算所得到的无论是总阻力阻力曲线还是 曲线与试验方法所得曲线吻合的相当好，其误差在允许的范围内，故该计算方法具有较高的准确性可以用来计算分析碟形潜器的水动力性能。

2）运用Fluent模拟得出的潜器周围的流场的速度云图和潜器表面的压力分布云图与潜器的实际情况所吻合，具有一定的准确性，可以用来形象得描述潜器的水动力性能。

3）同样可以看出随着Fr 数的增加模型的数值计算结果与水池试验结果之间均呈现渐大的偏差. 如何选择更合理的边界条件湍流模型（或其它封闭控制方程组的表达式）和数值算法等仍须作深入探讨，有待在后续的工作中加以改进.

参考文献

[1] 盛振邦，刘应中.船舶原理（上册）[M].上海：上海交通大学出版社，2003.

[2] 曾锋.动水域测算静水航速修正方法研究[D].重庆交通大学，2011.