浅谈统计学在工程中的应用

2015-06-29张毅余成起

四川水泥 2015年8期

关键词：读数间距概率

张毅余成起

（1.重庆市江津区四面山旅游集团公司，重庆 404100；2.四川省城市建设工程监理有限公司，四川成都 610000）

浅谈统计学在工程中的应用

张毅1余成起2

（1.重庆市江津区四面山旅游集团公司，重庆 404100；2.四川省城市建设工程监理有限公司，四川成都 610000）

统计学在许多领域都发挥着重要的作用，在我们的工程建设领域中也有统计学应用的例子。下面这篇文章将从我们工程中经常接触的混凝土强度和张拉力与油表读数的关系两方面来说明统计学在工程技术领域的应用，以及从数理统计的角度谈谈统计学在工程管理方面的应用。

统计学；工程建设；混凝土强度；张拉力

一、混凝土配制强度中统计学的应用：

《公路桥涵施工技术规范2000版》第199页附录F-4 混凝土配制强度计算里面应用如下公式RP=R+1.645σ（1）,公式（2）取自样本标准差计算公式，（注意：因为混凝土试件仅仅是混凝土结构总体的样本，故规范采用的是样本标准差计算公式，而不是总体标准差计算公式而公式（1）为什么配制强度要以设计强度等级加 1.645σ，这其中正是运用了统计学的原理。

我们配制混凝土，要求其至少达到设计强度，这样，混凝土的强度分布就成为一个数学期望值为设计强度R，分布幅度为σ的正态分布其中μ为设计强度R，x为混凝土样本的强度。）如图：

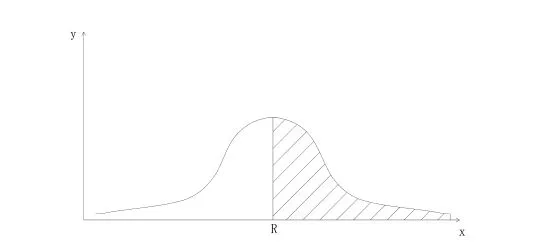
图1

其中阴影部分面积表示的是大于等于混凝土设计强度R的混凝土样本分布，这样就存在了一个问题：如果我们按照设计强度配制混凝土，那么，配制出来的混凝土大于设计强度和小于设计强度的概率各为 50%，无法保证混凝土强度达到设计要求。于是，我们人为提高混凝土的数学期望值为μ+1.645σ如图2：

图2

由图可见，当按提高后的强度的配置的混凝土样本强度大于设计强度的概率由原来的50%，提高到了（图中阴影部分面积）。那么提高了1.645σ的混凝土样本有多大的保证率呢，换句话说也就是图中阴影部分面积到底是多少呢？

1、查标准正态分布表1.64的概率为0.9495,1.65的概率为0.9505，内插可知1.645的概率为0.95，

从以上的分析可以得出结论：按照 R+1.645σ配制的混凝土能够达到 R的概率为95%，达不到R的概率为5%，而统计学上通常认为小于5%的事件为小概率事件，在实际中不太可能发生，从而保证了实际配制的混凝土的强度都能够达到设计强度。

二、张拉力与油表读数中统计学的应用

在预应力张拉施工过程中，首先要做的一件事情就是校顶，为什么校顶过后，检测单位会出具一张千斤顶压力和油表读数的关系表？最后的回归公式又是怎么来的呢？

首先我们知道油表读数与顶压力是有关系的，张拉力越大，油表读数越高，而且是成正比增加的，所以我们说油表读数和顶压力是一次线性相关的，基于此我们建立了Y=aX+b(Y是油表读数，X是顶压力)的回归方程，当试验室使用千斤顶达到各阶段的压力时，记录下油表读数及对应的压力，如下图：

取得一系列样本后，用最小二乘法计算出 a和 b，公式images/P99_67149.jpg（n为样本个数，为顶压力平均值，为油表读数平均值，xiyi为样本值），用公式求解计算量较大，现在可以使用4850计算器的DATA功能很方便的求出a，b值，其中a称为相关系数，a越接近1，则表示xy越相关，在实际工程中千斤顶压力和油表读数的相关系数a在0.99以上。利用这个方程，我们便可以方便的求出在任何顶压力下，油表的读数值。