不同土层中地下结构抗浮作用的试验研究

周明

(国家知识产权局专利局专利审查协作广东中心，广州 510006)

不同土层中地下结构抗浮作用的试验研究

周明

(国家知识产权局专利局专利审查协作广东中心，广州 510006)

本文通过模型试验的方法，对不同土层中地下结构所受浮力进行试验，主要探讨砾石、中砂和粘土中地下水对结构的浮力作用效应，通过水位的变化和对中砂中孔隙率的不同来探究浮力的变化规律，试图通过试验，来研究无粘性土与粘性土中浮力的作用之区别。

模型试验；砂土地基；地下结构；浮力

随着城市的发展，建筑有从多高层向地下要空间的趋势。特别近年来，各大中小城市在中国经济浪潮的带动下，人口压力和经济需求都迫使城市大量新建地下铁道和地下管廊以缓解交通压力，全国出现兴建地铁的风潮。目前，业界尚没有统一的抗浮理论依据和普遍让工程师信服的操作实践，甚至对其中的基本问题存在一些较大的分歧。所以一般的建筑抗浮设计中，从安全和保险起见，往往采用最高设防水位作为抗浮设计的依据，建筑所受浮力便简单的采用阿基米德定理进行估算。这种方法在工程上是偏于安全的，但是大量的工程实践表明，这样做会使工程造价很大程度的增加也同时增加了工程的施工难度。本文将试图探索无黏性土和黏性土中水浮力的作用机理，研究地下结构抗浮的分析方法，为后人更好地完善抗浮理论提供一定参考。

1 地下水浮力模型试验仪器和试验方法

在不同土层中，由于水-土颗粒的作用形式的差异性和复杂性，地下结构的所受浮力也不尽相同，室内模拟实验能尽量排除一些次要因素，相对于现场实验有较大的优势。因此，本次研究采用室内模拟的方法。为了规避试验模型的边界效应，采用两套大小规格不同的模拟同时进行试验。

本实验通过模拟地基和基础建立地下结构、地下水和土颗粒之间的力学关系，尽量使试验接近现场工况，又不掺杂多余因子。通过控制进水量，达到控制地下水水位的目的，再通过简单准确的测量系统求出测力环上等算出的压力，进而求出基础模型所受浮力。

2 无黏性土中的试验和结果

无黏性土一般包括碎石类土和砂类土，含黏粒非常少，不具有可塑性，结构为单粒类型。区别于黏性土，其物理性质主要取决于土的密实度。当呈密实状态时，强度较大，结构较稳定，是良好的天然地基；松散状态时，强度低，稳定性差，且压缩性大，是一种软弱的地基，特别是饱和状态的粉、细砂在振动荷载作用下易发生液化。评价砂土的密实度时，孔隙比是主要性质指标，不同孔隙比下的砂土有松散、稍密、中密和密实的不同密实状态。将通过对砾砂地基的浮力试验和不同孔隙率的砂土试验，来分析无黏性地基中的地下结构受浮力的影响。

在砂类土的浮力试验中，拟研究这样几个问题：摩擦力处理的几种方法、摩擦力与孔隙水压力的关系、浮力与孔隙度的关系和浮力与渗流的关系等等，介于此，砂类土试验分为三个渐进的过程：

一是砂类土在松散状态时的浮力试验，称为状态一，即往地基模型缸内填入砂时，不经捣密，模拟砂自然松散状态时的浮力及其相关影响；

二是砂类土在中密状态时的浮力试验，称为状态二，经过第一次升水出水，再经过人工压密，静置一周后，砂的密实状态改变，再进行试验；

三是砂类土在密实状态时的浮力试验，称为状态三，经过一和二状态的试验，砂类土已经相对密实，再次升水试验时，用振捣棒对砂类土进行捣密实，明显可见砂层下降且有气泡上冒，静置两周后，再进行试验。

状态一时，实测浮力与理论计算浮力的对比图1：

图1 实测浮力与理论计算浮力的对比

理论计算浮力的截距为其真实垫层厚度，实测浮力曲线和理论计算浮力曲线其拟合直线的斜率理论是相等的。从上面三组试验可是看出，随着砂的密实度的增加，浮力结果的理论值与进水实测浮力的差值是逐渐增大的，原因之一是地基模型与内缸侧壁的摩擦力处理有关，摩擦力到底随着砂土中的水位变化以否，这还需要进一步研究。

在砾石试验中，通过砾石曲线的截距法，绘制出的浮力曲线与纯水计算的浮力曲线几乎重合，这表明截距法有相当的可靠性。在中砂试验中，采用三组不同的密实度来研究中砂所受浮力以及影响浮力大小的其他因素。经过进水和出水试验，结果表明，砂类土的摩擦力因子与孔隙水无关。浮力也仅有水位成正相关。但随着砂类土的密实度增加，浮力曲线的斜率呈增加趋势，考虑其主要是由于侧壁摩擦力的影响。砂类土地基中的地下结构不应折减。

3 黏性土中试验和结果

黏性土的透水性较差，试验所用土为残积砂质黏性土，试验填土时，在地基模型下铺置8cm砾石，有利于底部进水的均匀性，内缸底下再垫有5cm黏性土，填土后静置两周。其试验周期较长，时间间隔较久，采用试验法确定在20小时后，读数基本稳定。每次升水后，隔5小时、10小时、20小时、30小时的间隔进行读数，每一个过程不少于三次读数。

图2 砂质黏性土试验

经过一个月的进水试验，基本能使水位下土样饱和，且读数呈现稳定。再通过类似砂类土的处理方法，将结果等算成浮力的曲线。利用每一过程的最后一个读数（认为是最后稳定读数），见图3。

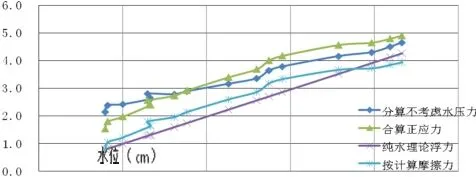
图3 黏性土浮力计算对比

从图表中可以看出，无论是合算计算的浮力相比分算的结果，在斜率上更接近理论的浮力，曲线的斜率可以看做是液体地基的重度和内缸面积的乘积γS，以前学者研究（崔岩）对于黏性土的浮力计算中，浮力的重力应该取其液体悬浊液，而非水的重度。本试验结果表明，在足够长的时间，在静水情况下，斜率的一致性证明砂质黏性土中浮力计算仍拟用水的重度。但是，图表显示结果又表明，合算所得的结果与纯水中的理论值存在一定的折减，大概为10%-20%之间。这个关系在本试验中尚不能确定，工程实践中不建议直接折减，还应该综合考虑黏性土中水的赋存形式、有无渗流。因为黏性土的不同流塑指数，土性差异相当大，而纯水中的理论值并不是浮力的真实值。

4 结论

经过对砾石和中砂进行浮力试验，在砾石试验中，通过砾石曲线的截距法，绘制出的浮力曲线与纯水计算的浮力曲线几乎重合，这表明截距法有相当的可靠性。在中砂试验中，采用三组不同的密实度来研究中砂所受浮力以及影响浮力大小的其他因素。经过进水和出水试验，结果表明，砂类土的摩擦力因子与孔隙水无关。浮力也仅有水位成正相关。但随着砂类土的密实度增加，浮力曲线的斜率呈增加趋势，考虑其主要是由于侧壁摩擦力的影响。砂类土地基中的地下结构不应折减。

主要对黏性土地基上中地下结构受浮力作用进行了研究分析，所得主要结论为：

（1）砂质黏性土一次读数的稳定时间大约为20小时，随着水位的上升，总体数据散点为线性分布。

（2）图表显示结果又表明，合算所得的结果与纯水中的理论值存在一定的折减，大概为10%-20%之间。这个关系在本试验中尚不能确定，工程实践中不建议直接折减，还应该综合考虑黏性土中水的赋存形式、有无渗流。

（3）以上两点表明，对饱和砂质黏性土地基，计算地下水浮力的水位折减程度不大，在计算浮力仍可采用水的重度。

［1］丁晓龙. 饱水介质中建筑基础浮力折减系数的试验测定方法［J］. 中国科技信息，2007，7：267-268

［2］梅国雄. 关于基础抗浮的若干问题探讨［J］. 岩土工程学报，2008，30（增刊）：238-242

［3］王建英. 建筑物抗浮设计中几个问题的分析［J］. 建筑技术，2005，36（7）：544-545

G322

B

1007-6344（2015）08-0070-01

周明（1985-），男，江西人，研究生学历，助理工程师，从事建筑工程类专利审查