一种新型可展结构的探索

宋依洁 熊海贝 卿紫菲 何子安

(同济大学土木工程学院，上海200092)

1 引言

1.1 可展概念与建筑

希腊学者 C.J.Gantes[1]对可展结构的定义是:可展结构是由预制单元集成的，能够从初始的紧密构型展开到预先确定的展开构型工作形态，从而成为具有承载能力的稳定的结构体系。20世纪 60 年代，美国建筑师 Buckminster Fuller[2]在建筑领域提出了可展结构的概念。西班牙建筑师Pineo[2]在此启发下，在世界建筑作品大奖赛中展示了跨度为300英尺的穹顶折叠式可移动剧院。西班牙学者Escrig和Valcarcel[3]在此基础上对可展剪式铰结构和整体稳定性进行了研究，成功建成了一个30 m×60 m的游泳馆可展穹顶。

2000年德国汉诺威世博会上，霍伯曼为Iris Dome[2]设计并建造了可缩回式的圆屋顶，通过四台电脑控制的液压气缸使得高6.2 m、宽10.2 m的圆屋顶逐渐收回。在建筑施工领域，日本的川口卫教授[4]提出的适用于双曲率网壳的攀达穹顶整体顶升施工方法已在世界上数个工程中得到成功应用。

1.2 剪式单元构成可展结构

许多空间可展结构都是由基本构件剪式单元[5]相互连接组成(图1(a))。本文重点介绍该种可展结构的设计。

将剪式单元进一步改进，把直杆换成折杆，就形成了可以调整角度的折线形剪式单元(图1(b))。折线形剪式结构的概念由 Kempe[6，11]提出，Hoberman[7-8]对其命名并且应用在各种可展结构设计中。在Hanaor[9]对可展结构的研究结果中，这种剪式结构常常是受弯控制，材料利用效率不高。

在此基础上，比利时的Mira[10-11]设计出了三角形剪式单元(Universal Scissor Component)(图1(c))，由三角形替换折线形杆件，能提高抗弯性能，减少变形。

图1 剪式单元Fig.1 Scissor elements

2 新型可展结构设计

2.1 设计过程

本文基于三角形剪式单元，从优化结构构型、减轻结构自重、适应实际工程需要的角度设计了一种新型空间可展结构。

本文制作了一个小比例模型，跨度2 m，矢高1 m。该结构以三角形剪式单元为基本单元组成剪式组合构件(图2)，顶部节点将六个剪式组合件连接形成空间可展体系(图3)，并采用钢丝拉索构成平面外支撑体系(图4)，结构底部采用围合杆件和径向导轨构成结构自平衡基础(图5)，综合组成了稳定性和伸缩性能均优的新型可展结构模型(图3、图5)。

可展机构展开的原理是每个剪式组合构件在平面内的收缩。剪式组合构件下端部的节点都安有2个滑轮(图3(a))，12个滑轮同时向中心滑动带动每个剪式组合构件的折叠，使得整个机构收缩。可展机构展开后，在将轮子和顶部节点的位置固定，便形成稳定的结构(图3(b))。

图2 三角形剪式单元组成剪式组合构件Fig.2 Composition of scissor composite members

图3 空间可展模型Fig.3 Composition of a deployable structure

图4 预拉力钢丝拉索Fig.4 Pre-tensioned ropes

图5 收缩模型及底盘Fig.5 Contraction state of the structure

2.2 设计注意事项

可展结构的设计主要是保证可展性能和稳定性的统一，特别是展开过程中的稳定可控性。应设计合理的轨道和驱动方式，在展开过程中增加临时的侧向支撑。

每个剪式组合构件在平面内只有一个自由度，只需增加一个链杆约束即可变成几何不变的结构(图6)。但设计时应加强结构整体刚度，例如展开后增加多个链杆和铺设刚性连接的面板，使结构能够抵抗设计荷载。结构较薄容易在平面外失稳，应仔细考虑风荷载的作用，设置足够的平面外支撑和围护体系，例如采用刚性的横向支撑或者柔性的预拉力拉索。通过调整三角形的高宽比或连接方式，可以设计出灵活多变的整体外形。对于跨度较大的空间结构，可以考虑用三角形桁架代替三角形单元组成剪式单元，减少杆件计算长度。

图6 增加一个链杆后几何不变Fig.6 Geometrical invariability by adding a constraint

3 试验研究

3.1 试验设计

本静力加载试验主要模拟屋面结构在承受竖向荷载工作状态下的结构反应。考虑竖向活荷载最不利布置，分全跨和半跨两种工况进行加载。图7为加载点及位移计布置图，括号内数值为位移计标号。静力试验方案如下:在结构顶部的节点(图7标号10)和每个剪式组合构件的跨中(图7标号1—6)施加集中荷载。

图7 加载点及位移计布置图Fig.7 Loading points and displacement meters

设计总荷载为 1.75 kN，底盘面积 3.14 m2，面荷载0.56 kN/m2。荷载分五级施加，工况1全跨加载时，分级加载表如表1所示。卸载试验与加载试验的顺序相反。

表1 全跨静载试验分级加载表Table 1 Table of the loading schemes

工况2半跨加载时，仅在相邻的三跨施加竖向荷载(图7标号1—3)，即上表中边跨总荷载减半，但每级中施加在每个剪式组合构件的荷载不变。

3.2 试验装置

在结构顶部、每个剪式组合构件的跨中挂置砝码施加集中荷载，见图8和图9。

图8 边跨砝码加载Fig.8 Loading at the mid-span

图9 顶点砝码加载Fig.9 Loading at the central node

试验中，在每个剪式组合构件的跨中部位布置了竖向位移计(标号1—6)。每隔一个剪式组合构件的跨中布置了水平位移计(标号7—9)。在中心节点处设置了一个水平位移计和一个竖向位移计(标号10和11)。位移计标点位置见图7数字标示(括号中数字表示水平位移计，其余表示竖向位移计)。下文中用竖向位移计的数字来代指该构件。

3.3 数据分析

按照加载表进行加载卸载试验后，采集荷载和位移数据，制成图表如下。

工况1全跨加载-卸载的荷载位移曲线如图10—12。图中VD代表竖向位移，HD代表水平位移，数字指代图7中的位移计标号。

图10 荷载—竖向位移曲线(全跨加载—卸载)Fig.10 Load-vertical displacement curves under full-span loading-unloading scheme

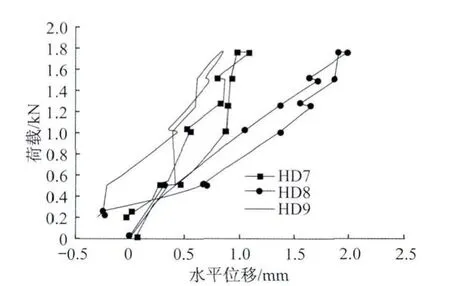
图11 荷载—水平位移曲线(全跨加载—卸载)Fig.11 Load-horizontal displacement curves under full-span loading-unloading scheme

铝合金模型施加总荷载1.75 kN时，结构的最大竖向位移7.9 mm(图12)发生在顶点处，挠度为1/250。5号、6号剪式组合构件的竖向位移明显大于其他(图10)，观察后发现5号、6号构件有初始缺陷，未受力时已微微翘起，加载后位移较大。加载时也出现了一些不均匀的水平位移。结构位移在卸载后都有明显恢复，说明设计荷载小于结构极限承载力，结构还有回弹能力。

工况2半跨加载时，在图7中标号为1、2、3的构件跨中施加半跨活荷载。其荷载位移曲如图13—图15所示。

图12 荷载—顶点位移曲线(全跨加载—卸载)Fig.12 Load-displacement curves for the central node under full-span loading-unloading scheme

图13 荷载—竖向位移曲线(半跨加载—卸载)Fig.13 Load-vertical displacement curves under half-span loading-unloading scheme

图14 荷载—水平位移曲线(半跨加载—卸载)Fig.14 Load-horizontal displacement curves under half-span loading-unloading scheme

半跨加载试验与全跨加载相比，总荷载减小，顶点位移稍减小，水平位移变大。半跨加载最大竖向位移7.1 mm(图15)也出现在顶点，挠度为1/281。1号点竖向位移次之为6.6 mm(图13)。最大水平位移5.4 mm出现在顶点。对该模型的静力试验结果说明该种可展结构具有一定的承载能力，能够满足实际需要。

图15 荷载—顶点位移曲线(半跨加载—卸载)Fig.15 Load placement curves for the top node under half-span loading-unloading scheme

4 应用前景

可展结构具有伸缩平滑，搭建、拆卸和运输方便，基本杆件相同能批量化生产等优点，可应用于永久半永久建筑以及空间结构施工技术中，例如应用于救灾帐篷、临时展馆等。实际上，可展结构作为永久性建筑仍然存在小规模生产成本昂贵，结构规模较大时结构与基础难以牢固连接等问题，仍需在实践中继续研究。

可展结构体系可以从机构变成结构，这一特点可应用于空间结构的施工技术中。空间结构在空间利用上是高效能的，但在施工方面却需要大量的脚手架，劳动力和时间，并且在还经常产生工程精度、可靠性和安全性等方面的困难。板状屋顶中经常采用的现代化施工方法如提升体系等不能等效地应用于曲面状空间结构中。可展结构被应用到穹顶状结构的施工体系中并非先例，日本政法大学川口卫教授提出了攀达穹顶(Pantadome)的施工体系。与之相似的，本文提出了一种新型可展结构施工体系的构想。

4.1 攀达穹顶施工体系

攀达穹顶体系的核心思想是通过临时去掉一些杆件使穹顶在施工阶段暂时变为一个机构，可以趴伏在地面上完成大部分施工工作，之后顶升到预定的高度就位。图7所示的穹顶状的网壳结构，去掉平面图中虚线所表示的杆件后，这个穹顶就形成了拆掉环向箍的状态，这样就可以简单地进行折叠了，在低空完成施工工作后再顶升就位[4]。

4.2 可展结构施工体系

本文提出一种新型的施工体系构想，在可展机构伸展变成稳定结构的过程中完成空间建筑的建造。

图16 攀达穹顶的施工原理Fig.16 Working principles of the Pantadome

这种施工体系由剪式组合构件和刚性顶盖组成，建造时先在地面上分别制作剪式组合构件和刚性顶盖。将剪式组合构件收缩成最小状态，再与刚性顶盖相连接。连接好之后将穹顶结构用液压千斤顶和临时支柱提升，顶升就位后在剪式单元之间施加链杆约束，最后在平面外铺设刚性面板形成稳定的空间结构(图17)。

依靠刚性顶盖的刚度和轨道的约束，该种施工体系在水平方向的运动是完全被约束住的，体系只在上下垂直方向有一个自由度。但由于剪式组合构件不可能做的太厚，顶升时剪式组合构件容易在平面外失稳，需要设置平面外的支撑和围护结构，在顶升时应附加侧向的刚性支撑来抵抗突然的地震和强风等水平荷载。

这种体系的优点是:顶升过程更加平缓简便，展开时的速度和运动轨迹更容易被计算机控制，轨道和驱动系统也容易设计。

图17 可展结构施工体系Fig.17 Construction of deployable structures

5 结论

本文提出了一种新型可展结构，该结构由圆盘节点、六榀剪式组合构件和围护体系组成，形成了兼具可展性与稳定性的空间可展结构。通过对模型的荷载试验得到，静力试验卸荷后，结构位移出现大幅回弹，结构的最大位移和挠度都在可接受范围内，说明结构在0.56 kN/m2的活荷载以及自重荷载下具有良好的承载能力和一定的抵抗变形能力。结构的初始缺陷和制作精度对变形有很大影响。

该可展结构搭建、拆卸容易，运输方便;相同的基本杆件用不同的拼接方式可以形成不同的几何外形;可在工厂预制、批量化生产，促进建筑工业化。因此该结构可应用于临时建筑，半永久建筑。该结构的展开过程平缓稳定，只需要稍加稳定措施就可以顶升重物。因此可以考虑应用于新式施工体系，经济便捷。

[1] Gantes C J.Deployable structures:analysis and design[M].Greece:National Technical University of Athens，2001.

[2] Friedmin N.Investigation of highly flexible，deployable structures:review，modelling，control，experiments and application[D].Budapest:Budapest University of Technology and Economics，2011.

[3] Escrig F，Valcarcel J P.Geometry of expandable space structures[J].International Journal of Space Structures，1993，8(1):127-134.

[4] 王小盾，石永久，王元清，等.一种新型的穹顶结构施工体系—攀达穹顶施工方法[J].建筑科学，2005，21(5):87-91.Wang Xiaodun，Shi Yongjiu，Wang Yuanqing，et al.A new construction method for dome structure—pantadome system[J].Building Science，2005，21(5):87-91.(in Chinese)

[5] 熊天齐.可展结构理论分析与研究[D].上海:同济大学，2006.Xiong Tianqi.Analysis and study of deployable Structure[D].Shanghai:Tongji University，2006.(in Chinese)

[6] Hoberman C.Reversibly expandabledoubly-curved truss structures，United States Patent 4，942，700.1990

[7] Hoberman C.Radial expandable/retractable truss structures，United States Patent 5，024，031.1991

[8] You Z.Motion structures extend their reach[J].Material Toda，2007，10(12):52-57.

[9] Hanaor A and Levy，R.Evaluations of deployable structures for space enclosures[J].International Journal of Space Structures，2001，16(4):211-229.

[10] Mira L A.Design and analysis of a universal scissor component for mobile architectural applications[D].Brussel:Vrije Universiteit Brussel，2010.

[11] De Temmerman N，Mira L A，Vergauwen A.Feasibility of the universal scissor component(USC):building a full-scale deployable dome[J].Journal of the International Association for Shell and Spatial Structures(J.IASS)，2012，53(4):227-236.