初应变作用下一对边固支一对边简支矩形薄板的弹性理论分析

王 懿

（贵州交通职业技术学院，贵州 贵阳 550008）

初应变作用下一对边固支一对边简支矩形薄板的弹性理论分析

王 懿

（贵州交通职业技术学院，贵州 贵阳 550008）

初应变作用下一对边固支一对边简支矩形薄板，可看作是初曲率作用下的四边简支板与一对边作用力矩的四边简支板的叠加，在位移协调条件下可导出初应变引起的板内力的表达式和挠度方程，并可编程进行验算。

矩形薄板 初应变 叠加原理 内力 挠度

初应变作用下屋面板的工作环境和边界条件具有其复杂性和特殊性，本文对边界条件为一对边固支一对边简支的矩形薄板进行了理论分析，以期对规则屋盖在初应变作用下的效应产生较明析的认识。

1.问题的模型建立

根据叠加原理，初应变作用下的一对边固支一对边简支矩形薄板的应力问题，可看作是初曲率0κ作用下的四边简支板与一对边作用力矩Sm的四边简支板的叠加，如图1所示。

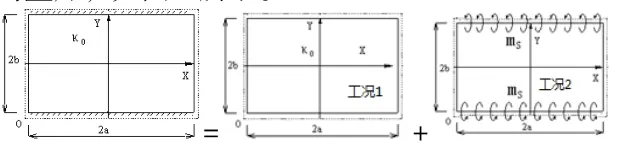
图1 矩形薄板计算示意图（0κ：板变形凹口向上为正）

2.问题的解答

2.1 工况1

考虑到板的对称性以及初曲率本身作用的对称性，设挠度表达式和边界条件：

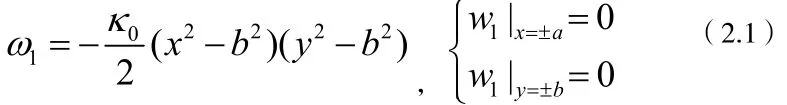
2.2 工况2

运用Levy法，问题的边界条件为：

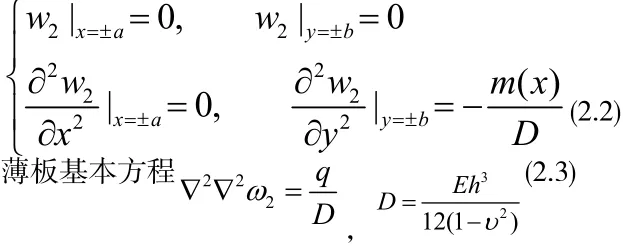
对于所分析的问题0q=，针对（2.1）（2.2）所确定的基本方程及边界条件工况2的挠度函数以双曲三角函数及一般三角函数混合级数形式设为：

联立以上公式求解，便得到工况2下挠度的最后表达式：

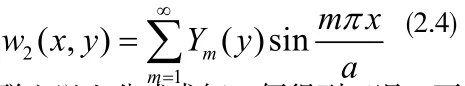
m = 1

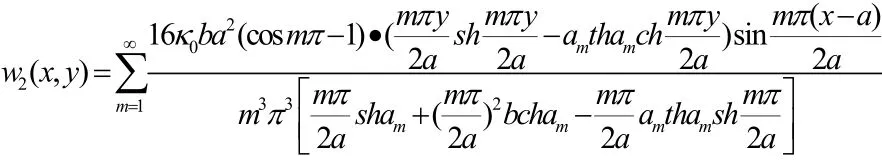
（2.7）

2.3 初应变作用下一对边固支一对边简支矩形板挠度内力表达式

运用叠加原理，一对边固支一边简支矩形板挠度w为工况1挠度1w与工况2板挠度2w的组合：

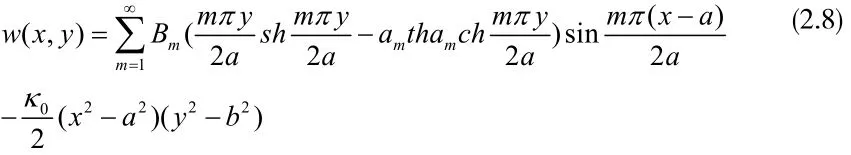
用已求得的挠度w计算板弯曲内力解函数为：

式（2.8）、（2.9）为本文导出的初曲率作用下一对边固支一对边简支矩形薄板产生的弯矩与挠度函数表达式。

3.算例分析

3.1 计算模型

计算模型的条件为：长宽6m×5m，板厚分别取0.12m、 0.16m、 0.20m ，混凝土的强度等级为C30，其泊松比υ=0.2，弹性模量E=3× 1010N/m2，线性膨胀系数α=1× 10-5/0C ，计算温度工况为：屋面板初曲率κ0分别取0.001、 0.0015、 0.002。

3.2 结果分析

根据式(2.8)、(2.9)编写程序，分别计算不同工况下板中各点的挠度和内力，计算结果如下图所示。

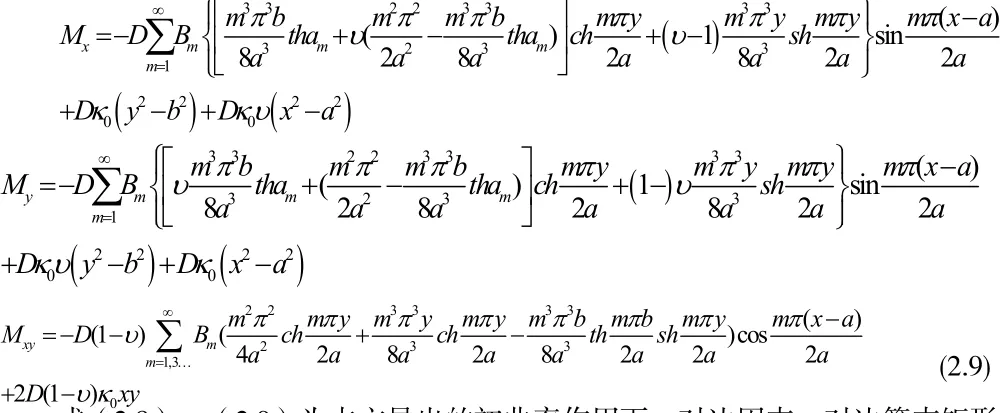
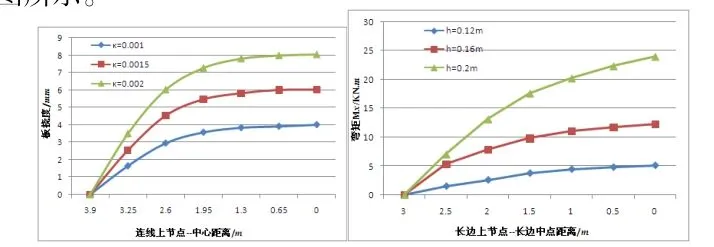
图2 板挠度w分布图图3 沿长边X轴方向跨中弯矩Mχ图（h=0.2m） （κ0=0.001）

（1）对边固支一对边简支矩形薄板在初应变作用下时，可按式(2.8)、(2.9)算其挠度和内力,计算结果可靠。

（2）由图2，板中挠度随着初应变作用的增加成正比关系；而在初曲率κ0=0.0015作用下，板的最大挠度出现在跨中，仅为6.027mm，远小于《混凝土结构设计规范》中正常使用极限状态验算下对屋盖挠度的规定值l0/200=25mm，可见初应变κ0对板挠度的影响并不大。

(3)由图3，当板厚h=0.2m,κ0=0.002时，Mχ(max)=-24.05kN.m ，板单位宽度最大弯矩出现在约束最强的固支边附近。

[1]程选生等.热载下三边简支一边固支矩形薄板的解[J].低温建筑技术,2007,4:59-62.

[2]张福范.弹性薄板[M].北京:科学出版社,1984,8,11-13,33.

[3]付宝连.弹性力学中的能量原理及其应用[M].北京:科学出版社,2004,319-320.

[4]周小龙，丁圣果.混凝土屋盖温度应力分析[J].山西建筑，2008，34（32）：5-6.

[5]周小龙，丁圣果.温度荷载下薄板的弹性理论分析[J].贵州大学学报，2009，26（3）：106-109.

G322

B

1007-6344（2015）04-0345-01

王懿，男，1986年11月28日生，汉族，贵州遵义人。学历：贵州大学硕士研究生，专业：结构工程。现为贵州交通职业技术学院建筑工程系讲师，工程师。研究方向：建筑结构多构件协同工作效应。