基于粒子群优化算法的地铁列车节能运行研究

孙其升 胡文斌 陈 磊 吕建国

(南京理工大学自动化学院，210094，南京//第一作者，硕士研究生)

城市轨道交通的节能研究主要体现在再生制动能量的利用率上［1］。文献［2-3］在研究动态规划算法、梯度算法及序列二次规划算法的基础上，通过上述算法优化列车的运行速度曲线及储能设备的充电状态，仿真结果显示算法的可行性与有效性;文献［4-6］主要研究了城市轨道交通列车牵引过程中的惰行控制策略，在单列车牵引仿真的基础上，采用各种搜索算法，如经典的黄金分割搜索、梯度搜索以及遗传算法等，寻找惰行位置点，优化列车节能和准时的目标函数;文献［7-8］在研究地铁列车单质点模型的基础上提出多质点模型，使列车运行模型更加符合地铁列车的实际运行情况;文献［9］提出了定时约束条件下的列车节能优化操纵模型及算法;文献［10］在分析列车运行的基础上致力于列车模拟软件的研究。

本文在建立地铁列车运行物理模型的基础上，采用粒子群优化算法搜寻列车区间运行的惰行点位置，优化列车区间运行时间及区间运行能耗，并利用南京地铁2号线提供的线路实际参数，对列车区间运行作定时节能策略研究。优化结果显示，区间运行时间满足要求的前提下，区间运行能耗大幅下降。

1 列车区间运行状态力学分析

地铁列车运行时，运行时分和能耗取决于牵引、制动、匀速和惰行4 种工况的有效分配，对应即形成运行时间最小的节时运行控制策略、运行能耗最小的节能运行控制策略及运行时间与运行能耗综合最优的定时节能运行控制策略。列车运行状态示意图如图1所示。

列车在区间的运行可以描述为:列车以初速度v0=0 从始发站开始运行，要求在给定时间t 内到达终点站，运行距离为S，运行末速度为vn=0。设列车运行过程中受到的牵引力为Fq，运行阻力为Ff，制动力为Bz，则列车受到的合力为C。其中:列车在起动加速过程中受到的合力为C加=Fq-Ff;制动减速过程中受到的合力为C减=-Bz-Ff;惰行过程中受到的合力为C惰=-Ff。若列车在所受合力作用下的加速度为a，列车运行计算递推过程如下:

图1 列车运行状态示意图

式中:

Mh——载客列车换算质量，kg;

Si——第i 次计算时列车的运行距离，m;

Si+1——第i + 1 次计算时列车的运行距离，m;

vi——第i 次计算时列车的运行速度，m/s;

vi+1——第i + 1 次计算时列车的运行速度，m/s;

Ei——第i 次计算时列车的运行能耗，kW·h;

Ei+1——第i+1 次计算时列车的运行能耗，kW·h。

2 优化模型

关于列车的定时节能优化，主要方法为:列车在运行过程中采用惰行方式，以节能为优化目标，定时为约束条件，寻找最优的惰行点开始位置和结束位置，保证列车在区间定时、节能运行。

2.1 地铁列车运行优化模型目标函数

列车在某一运行区间的速度曲线如图2所示。列车在该区间的运行采用惰行方式控制，有牵引、匀速、惰行、制动4 种工况。既有研究表明:区间运行时间一定时，列车以匀速牵引运行克服的基本阻力功最小;列车以最大加速度加速可减小加速过程中的基本阻力功;列车以最大制动力制动有利于节能;列车制动前惰行以降低制动前运行速度有利于减少列车动能损失［11］。因此，列车从A 站出发后，首先牵引运行至最大速度，然后匀速运行至D1开始惰行，运行至D2停止惰行开始制动，到B 站停车。图中列车只有1 次惰行，实际运行列车可采用多次惰行过程。列车定时节能优化的问题即转化为:列车运行时间变化满足要求的条件下，寻找惰行点的开始位置Di和结束位置Di+1，实现运行能耗最小。列车实际运行时间与列车最小运行时间之差不超过最小运行时间的8%［9］。

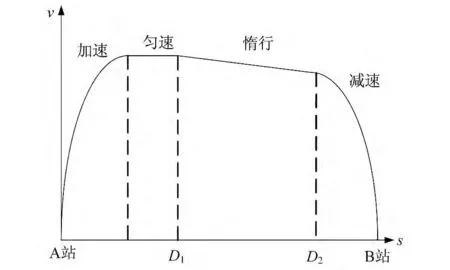
图2 基于惰行的列车运行速度曲线

保证列车区间运行时间满足要求的前提下，优化列车运行能耗模型的目标函数为:

式中:

WE，Wt，Wv——分别为能耗权重系数、时间权重系数和速度权重系数，WE+Wt+Wv=1;

α，β——分别为超时惩罚因子和超速惩罚因子;

tr，tp——分别为实际运行时间和最小运行时间，s;

Er，Ep——分别为实际运行能耗和最小运行能耗，J;

vr，vp——分别为列车实际运行速度和最高运行速度，m/s。

2.2 地铁列车运行优化模型目标约束

列车从A 站出发在规定的时间内运行至B 站，满足如下约束条件。

距离约束:

式中:

t——规定的列车运行时间，s;

S——A 站至 B 站的距离，m。

时间约束:

限速约束:

式中:

vi——第i 次计算时列车的运行速度，m/s;

vmax——列车运行限速，m/s。

边界条件:

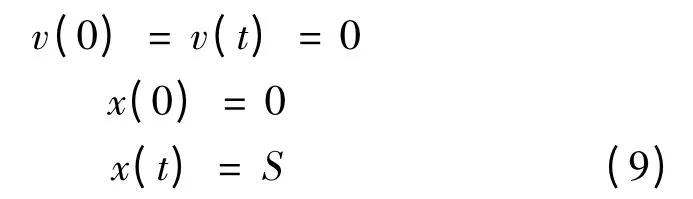
式中:

v(0)，x(0)——分别为列车运行起点速度和位置;

v(t)，x(t)——分别为列车运行终点速度和位置。

惰行点约束:

式中:

Di——第 i 个惰行点位置;

Di+1——第i+1个惰行点位置。

3 模型求解

粒子群算法是研究鸟类个体与群体协作、竞争行为发展起来的具有高度并行、随机、自适应的搜索算法，特别适用于传统搜索算法难以求解的非线性约束问题。

应用粒子群算法求解列车运行惰行控制优化模型时，求解之前先要确定适应度函数表达式、寻优代数、群体大小及搜索空间维度等参数。

惰行优化问题就是寻找惰行点位置的问题。惰行开始与结束的位置作为粒子群算法的n 维搜索空间的变量(n 一般小于4)，设定群体规模，随机生成初始化种群，种群中个体参数要满足约束条件Di≤Di+1;适应度函数如式(5)所示，寻找最小适应度值;确定个体最好位置及全局最好位置。

算法的基本流程如图3所示。

图3 粒子群算法计算流程

(1)初始化种群，对微粒群中的n 维搜索空间变量{D1，D2，…，Dn}的随机位置和速度进行初始设定;

(2)依据式(5)定义的适应度函数，计算相应的适应度值;

(3)对于每个n 维搜索空间微粒，将其适应度值与所经历过的最好位置{Db1，Db2，…，Dbn}的适应度值进行比较，若较好，则将其作为当前的最好位置;

(4)对每个n 维搜索空间微粒，将其适应度值与全局最好位置{Dgb1，Dgb2，…，Dgbn}的适应度值进行比较，若较好，则将其作为当前全局最好位置;

(5)对n 维搜索空间微粒的速度和位置进行进化;

(6)判断是否满足程序终止条件，如果满足则进行步骤(7)，不满足则返回步骤(2);

(7)输出结果，输出每个运行区间的列车能耗和运行时间。

其中，各惰行点数列对应的能耗和运行时间的计算步骤如图4所示。

(1)设置列车起始点s0和终止点s1，初始化列车惰行点位置值pos［n］;

(2)计算列车的总质量，包括拖车质量、拖车数、动车质量、动车数以及满载率等;

(3)初始化列车运行的初始状态，包括列车初速度 v0=0，加速度 a0=0.8 m/s2，初始位置 s0=0，运行时间t0=0，位置标志(ID)为0，列车受电弓电流Inet=0，消耗能量E=0;

(4)进入迭代，不满足结束条件则进行步骤(5)，满足条件则结束输出结果，生成报表，作出列车运行图;

(5)计算列车运行速度、运行距离;

(6)计算列车运行加速度，加速度的计算需要预先计算列车的牵引力、阻力以及判断列车运行工况;

(7)计算列车的电压、电流、功率;

(8)计算列车的消耗能量和回馈能量。

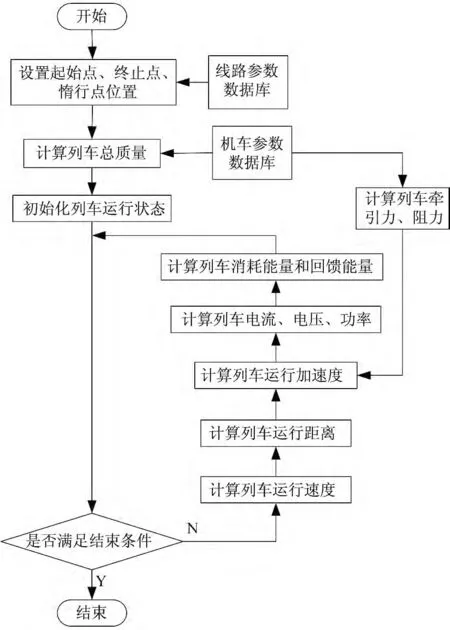
图4 列车运行状态计算

4 算例分析

选取南京地铁2号线莫愁湖—汉中门区段分析列车定时节能优化。待优化区段长995 m。考虑实际线路坡道和弯道，列车限速为70 km/h。列车相关参数见表1。粒子群算法中需要的相关参数见表2。

表3 为南京地铁2号线莫愁湖—汉中门区段运行仿真及优化结果，其中定时节能模式和定时节能2 模式为采用粒子群算法计算时分别加入了1 次惰行和2 次惰行。三种模式对应的列车运行速度v、距离S、列车受电弓电流I 对于列车区间运行时间t 的波形如图5所示。由表3 可以看出:①列车采用定时节能模式后，列车的运行时间较节时运行模式增加了3.98 s，能耗减少了6.04 kW·h，馈能减少3.71 kW·h，列车运行时间增加5.5%，列车运行能耗却降低了18.73%;②莫愁湖—汉中门区段惰行转换1 次和2 次对于优化结果无影响。

表1 列车相关参数

表2 粒子群算法相关参数

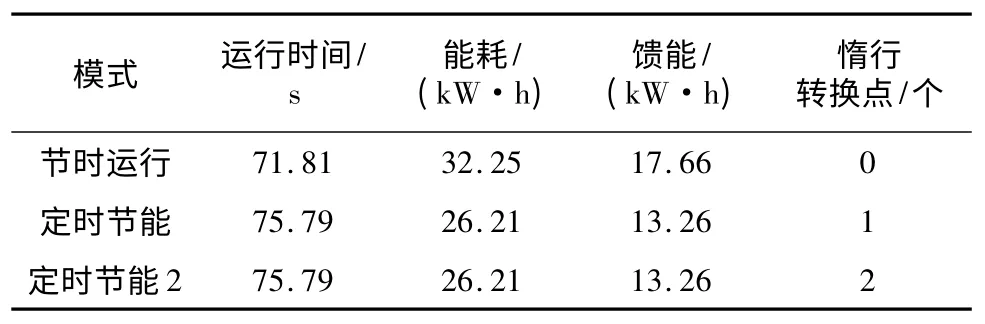
表3 列车在莫愁湖—汉中门区段运行的仿真及优化结果

表4 列出地铁列车采用粒子群算法优化2 个不同区间惰行点的开始与结束位置的结果。其中莫愁湖—汉中门区间长995 m，马群—金马路区间长3 021 m。从表中可见:莫愁湖—汉中门区间采用2次惰行时，2 次惰行节点位置相近，近似于1 次惰行;而马群—金马路区间2 次惰行节点区别明显，且2 次惰行和1 次惰行相比运行时间增加了0.42 s，能耗减少了0.6 kW·h。因此，列车运行模式选择应根据运行区间长度及运行线路坡道和弯道情况加以确定。

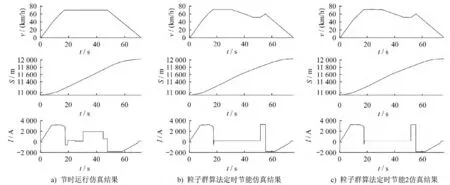
图5 莫愁湖—汉中门区段运行的仿真及优化结果

南京地铁2号线全区间优化前和优化后的列车运行速度曲线如图6所示。由图可见:区间长度小于1 km 时，采用1 次惰行;区间长度大于2.5 km时，采用2 次惰行;区间长度在两者之间时，根据实际线路情况决定。

表4 不同区段运行优化后惰行点位置

图6 列车运行全区间速度-距离曲线

5 结 语

本文在国内外研究成果的基础上，结合南京地铁2号线列车运行的基本参数，利用粒子群算法搜寻列车区间运行的惰行点位置，仿真分析南京地铁2号线实际线路区段优化前和优化后列车运行v-t、S-t、I-t 曲线，比较各区段列车运行时间及运行能耗，得出结论:粒子群算法可满足定时节能的优化要求，且区间运行时间增加5.5%，列车运行能耗相应降低18.73%。本文优化前后列车最大运行速度不变，如果实际列车运行限速提升10%，节能空间将进一步提升。

［1］Gunselmann W.Technologies for increased energy efficiency in railway systems［C］//Power Electronics and Applications，2005 European Conference on IEEE，2005(10):10.

［2］Miyatake M，Ko H.Optimization of train speed profile for minimimum energy consumption ［J］.IEEJ Transactions on Electric Engineering，2010，5(3):1.

［3］Miyatake M，Matsuda K.Energy saving speed and charge/discharge control of a railway vehicle with on ‐ board energy storage by means of an optimization model［J］.IEEJ Transactions on Electrical and Electronic Engineering，2009，4(6):771.

［4］Wong K K，Ho T K.Dynamic coast control of train movement with genetic algorithm［J］.International Journey of Systems Science，2004，35(13-14):835.

［5］Wong K K，Ho T K.Coast control for mass rapid transit railway with searching methods［J］.IET Electric Power Applications，2004(3):365.

［6］Wong K K，Ho T K.Dwell-time and run-time control for DC mass rapid transit railway ［J］.IET Electric Power Applications，2007(6):956.

［7］石红国.城市轨道交通牵引计算算法［J］.交通运输工程学报，2004，4(3)，30.

［8］石红国.城市轨道交通牵引计算模型［J］.交通运输工程学报，2005，5(4)，20.

［9］丁勇，刘海东，栢赟，等.地铁列车节能运行的两阶段优化模型算法研究［J］.交通运输系统工程与信息，2011，11(1)，96.

［10］毛保华.列车运行计算与设计［M］.北京:人民交通出版社，2010.

［11］钱立新.世界高速铁路技术［M］.北京:中国铁道出版社，2003.