城市轨道交通进站客流量短时预测模型研究＊

刘美琪 焦朋朋 孙 拓

（北京建筑大学土木与交通工程学院，100044，北京∥第一作者，硕士研究生）

随着城市轨道交通实时交通信息系统的日益完善，管理者需要掌握未来短时间内客流量的变化趋势，以制定和实施交通管理计划，这不仅可以使交通管理逐步走向智能化、动态化和信息化，还能提高运营效率，同时为出行者提供高效方便的服务。

在城市轨道交通日客流预测方面，文献［1］利用马尔科夫链改进了灰色模型；文献［2］将神经网络和支持向量机两种方法融合在一起，得到了组合预测模型；文献［3］则在前人研究的基础上，建立了基于客流时序特征的神经网络模型。在城市轨道交通短时客流预测方面，BP 神经网络［4－5］与小波神经网络［6］被引入组合模型。

非参数回归模型（Nonparametric Regressive Model）与神经网络模型同属于无数学模型的预测方法，但多用于道路交通流短时预测。文献［7］最早真正将非参数回归的方法应用到了交通流量预测中。文献［8］对传统的非参数回归进行了改进，运用变K 搜索算法和基于动态聚类和散列函数的历史数据组织方式。文献［9］利用该模型预测伦敦环路的交通量；文献［10］则应用到了快速路行程速度的预测。此外，卡尔曼滤波［11］、目标导向的神经网络算法［12］、模糊神经网络［13］与贝叶斯组合神经网络算法［14］均被引入预测模型中。

非参数回归模型适用于非线性和非平稳性的数据序列，但很少应用于轨道交通客流量预测。因此，本文为预测每5 min的进站客流量，分别建立了K近邻非参数回归（NPR）、基于偏差修正系数的卡尔曼滤波（KF）以及贝叶斯组合（BCM）模型，通过对比分析各模型在早高峰、晚高峰、平峰时段和全天的预测误差指标，发现K近邻非参数回归比其他模型的预测精度更高，对突发客流的处理能力更强。

1 预测模型

如图1所示，首先应用NPR 预测某站点两天的短时进站客流量，两天的预测值是为组合模型做准备，算法主要分为4步：历史数据准备及样本数据库生成、状态向量定义、K近邻搜索、预测算法。然后应用传统卡尔曼滤波模型预测前一天的客流量，拟合偏差修正系数，将系数引入观测方程并预测后一天的短时客流量。最后将前一天作为历史特征天，后一天的各时段作为贝叶斯组合预测模型中的当前时段，分别计算误差及贝叶斯权重，代入模型得到预测结果。

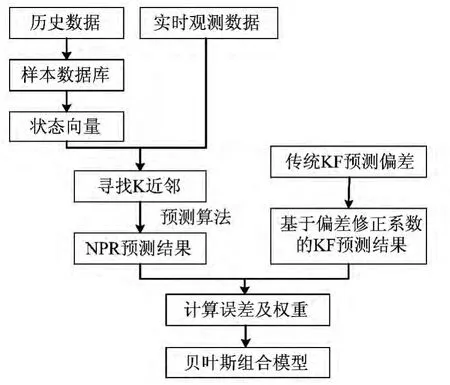
图1 算法流程

1.1 NPR 模型

NPR 是应用很广泛的一种非参数回归算法，具有无参数、可移植、预测精度高等优点，它的误差比较小，且误差分布情况良好。

1.1.1 历史数据准备及样本数据库生成

样本数据库由表示系统状态的全部历史观测资料组成，NPR 预测的效果和质量直接取决于样本数据库的质量。交通系统状态的特征蕴含在历史数据中，历史数据越多，越有利于非参数回归更加真实且完整地表达系统状态的特征，越有利于得到精确的预测值。样本数据库是动态的，它会随着观测数据的生成而不断更新，因此这是一个实时库与历史库相结合的复合数据库。

1.1.2 状态向量的定义

在交通领域，状态向量是指与预测站点当前时段的流量相关联的影响因素组成的向量。地铁站点吸引的客流量与路段交通量不同，它没有明确的上下游路段，没有信号灯，但是与预测站点相邻的其它站点的布置会影响客流量的分布及到达规律。所以在本文中，引入预测站点与其它站点之间的相关性分析，以相关系数ρAB的大小来确定状态向量中的相关站点数，同时状态向量还应包括预测站点前m个时段（t，t－1，t－2，…，t－m）的流量数据，m的取值可以通过计算m阶自相关系数ρm来确定。

将站点A连续n个时间段的客流量看作时间序列｛V1，A，…，Vn，A｝，站点B的客流量时间序列为｛V1，B，…，Vn，B｝，两站点之间的相关系数

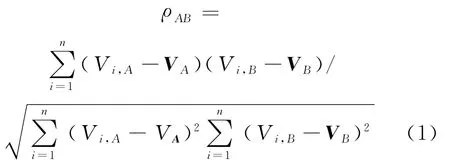
式中：

VA——站点A时间序列的平均值；

VB——站点B时间序列的平均值。

计算自相关系数时，将预测站点连续n个时间段的进站流量看作时间序列｛V1，…，Vn｝，把这组时间序列分解成｛V1，…，Vm＋1｝，｛V2，…，Vm＋2｝…｛Vn－k，…，Vn｝共n－m组子序列，设其m阶自相关系数

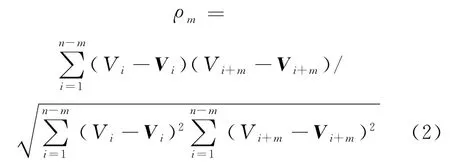
式中：

Vi——第i个子序列的平均值。

1.1.3 K 近邻搜索

K近邻法则是一种基于数据的非参数回归方法，它并非建立一种数学预测模型，而是寻找与当前状态向量相匹配的K个最近邻的数据，并以该K个数据的下一时段的数据为基础，对站点下一时段的值进行预测。

在样本数据库中搜索与实时数据相匹配的数据系列时，主要采用欧氏距离作为主要指标，即当前状态向量的各分量与历史状态向量中各分量的离差平方和的开方值，以此作为匹配距离，表达式如下：

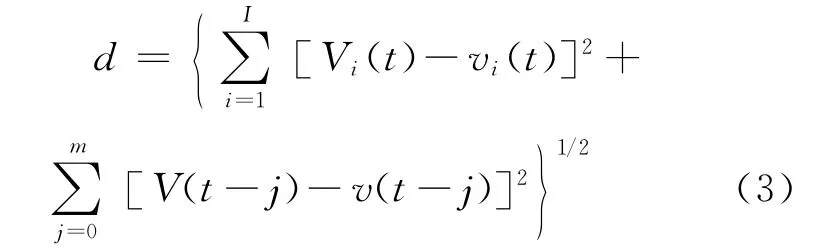
式中：

I——与研究站点相关的其它站点集合；

m——状态向量中研究站点前m个时段；

Vi（t）——站点i在时段t的进站流量；

vi（t）——历史数据中站点i在时段t的进站流量；

V（t－j）——研究站点当前状态t－j时段的进站流量；

v（t－j）——研究站点历史数据中的进站流量。

1.1.4 预测算法

设Vi（t）是时段t第i个近邻的进站客流量，di是其与当前状态向量之间的欧氏距离，则下一时段的客流量

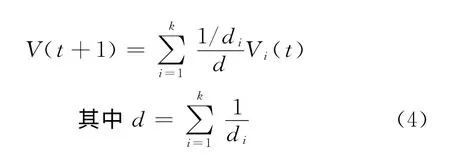
1.2 基于偏差修正系数的卡尔曼滤波模型

传统卡尔曼滤波模型尽管递推效率高，但由于其对历史信息的利用率较低，导致预测结果稳定性不强，所以为了提高其精度，在改进的观测方程中引入了偏差修正系数ω。地铁进站客流量随着时间序列存在平峰和高峰的变化规律。用传统卡尔曼滤波模型预测历史特征天的短时客流量，发现预测偏差（实际值减去预测值的绝对值）也存在平峰、高峰、先增后减的变化规律，用二次抛物线来拟合这种趋势。抛物线通过原点与偏差最大点，令a、b为常数，表达式为：

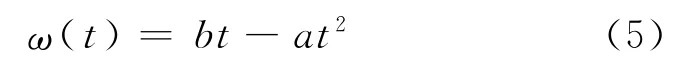
在不同条件下，修正系数的函数表达式不同，但是均与偏差的变化规律有关，所以修正系数的函数需要基于历史数据拟合得到。然后建立基于偏差修正系数的卡尔曼滤波模型，该模型包括状态变量、状态转移方程和观测方程3个核心部分。

状态变量确定为Q（t），即时段t预测站点的实际进站流量。状态转移方程为：

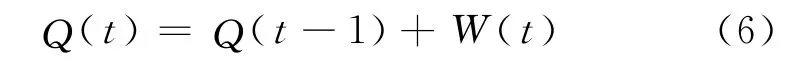
其中W（t）是状态方程的高斯白噪声序列。观测方程为：

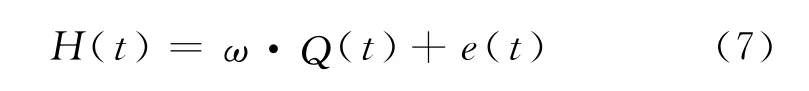
其中H（t）为时段t地铁站点的历史平均客流量；e（t）是高斯白噪声序列。

1.3 贝叶斯组合预测模型

根据贝叶斯定理，建立组合模型：

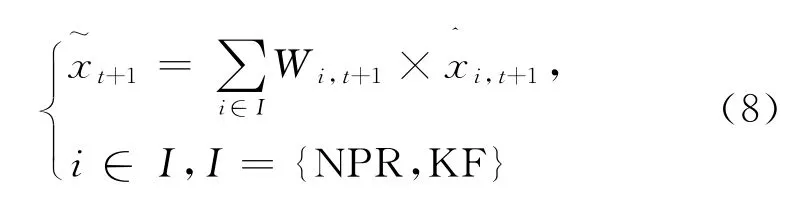
式中：

I——模型的集合；

NPR——K近邻非参数回归模型；

KF——代表基于偏差修正系数的卡尔曼滤波模型；

Wi，t＋1——模型i在t＋1时刻的权重。

2 实证研究

基础数据是北京市地铁13号线2013年11月份的进站客流，站点以编号来表示，分别为21、23、25、27、29、33、35、37、39、41、43、45、47、49和51。编号顺序按照实际站点顺序排列。本文以25号站点为研究对象，5 min为一个时段，从4：45至24：00，共分为231个时段。卡尔曼滤波模型和贝叶斯组合预测模型需要历史偏差数据，所以将11月21日（星期四）定为历史特征天，11月28日（星期四）确定为研究天。本节以NPR 的预测过程为重点，首先论述状态向量及K值的确定过程，然后对比分析28日各模型全天、早晚高峰和平峰时的预测误差。

2.1 确定状态向量及K值

2.1.1 状态向量的定义

状态向量通常选择与预测站点的交通状态最为相关的因素，因此本文选择相邻站点当前时段和预测站点前m个时段的进站客流量，通过计算相关系数ρAB及ρm来确定，相关系数取值在－1和1之间，且绝对值越大相关性越大，如图2所示。

25站点与21、23、27和49的相关系数绝对值都超过了0.9，但是49站距25站比较远，所以排除这个选择，以21、23和27站的当前时段客流量V21，V23，V27为状态分量。此外，状态向量还包括预测站点前m个时段，如图3所示，通过比较25站点自相关系数ρm绝对值的大小，确定m＝2。综上，状态向量X（t）＝｛V21（t），V23（t），V27（t），V25（t－1），V25（t－2）｝。

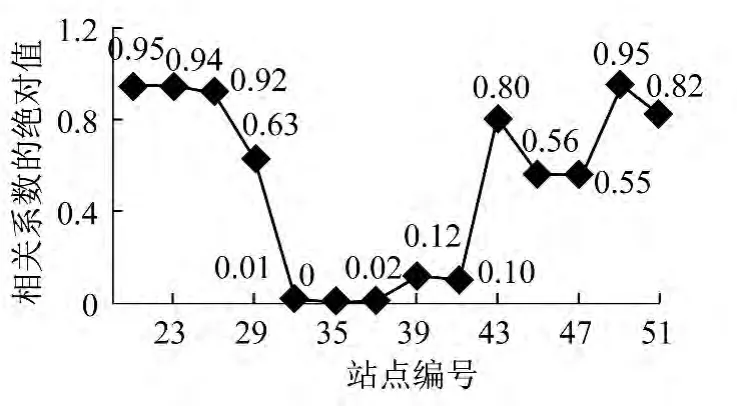
图2 25站点与其它站的相关性对比

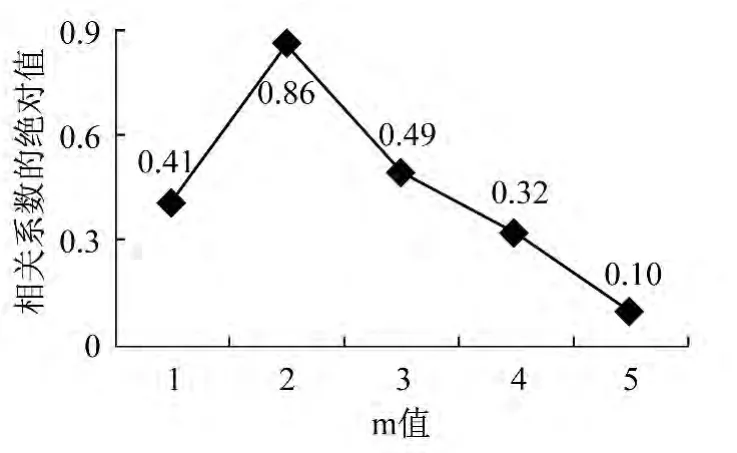
图3 25站点自相关系数

2.1.2K值的选取

状态向量确定后，在样本数据库中寻找和当前状态特征相似的K个近邻，然后进行预测。一般是通过逐渐增加K值，观察其对预测结果的影响，来确定最优K值。评价指标选取均方根误差ERMS、标准均方根误差在ENRMS、平均绝对百分误差EMAP和平均百分比误差EMP。令时段i的预测值为Pi，实测值为Ai，表达式如下：

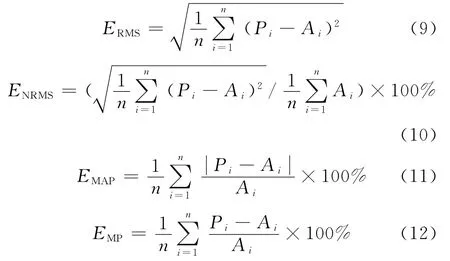
K取值从1至5，预测早晨4：45至凌晨24：00的进站客流量，并计算误差指标。如表1所示，当K＝2时ERMS、ENRMS、EMP值最小，EMP的值与最小值只相差1%，即0.01，所以K＝2是最优值。

2.2 各模型预测结果

2.2.1 误差指标对比

对全天5：00—24：00每5 min的客流量进行预测，误差指标如表2所示。

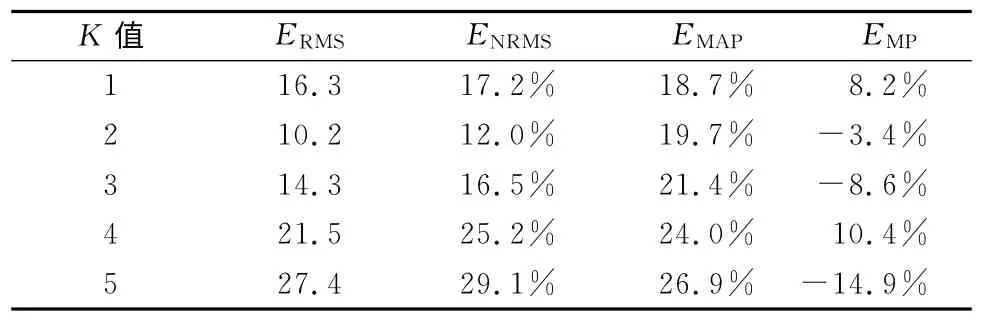
表1 不同K 值的误差指标

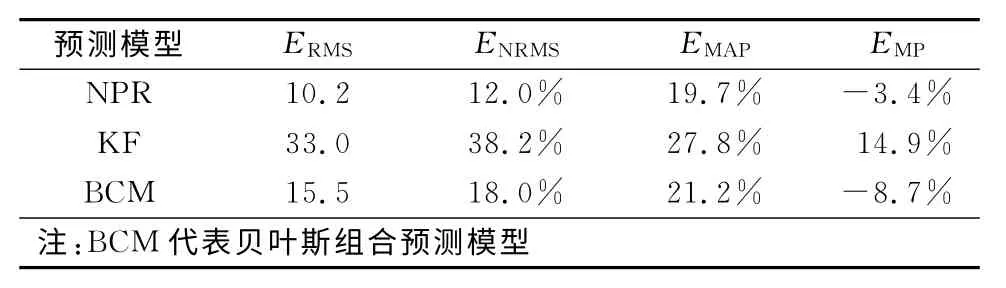
表2 模型误差指标

可以发现NPR 的预测精度最高，KF 的预测精度最低。由于BCM 权值分配规则是误差大的权值较小，误差小的权值较大，所以BCM 各项误差指标值在两子模型之间，且平稳性较好。

一般城市轨道交通的早高峰为7：00—9：00，平峰为11：00—13：00，晚高峰为17：00—19：00。预测每5 min的客流量，对比三类模型在不同时间段的ERMS，如表3所示。

由表3 可见：早高峰期间，NPR 的ERMS值最小，预测精度最高；KF 与BCM 的EPMS差值相近。平峰期间，BCM 的EPMS精度最高，说明在客流量小且平稳度增高的情况下该模型预测精度会提高。晚高峰时KF的EPMS值远大于早高峰、平峰与全天的EPMS，说明面对客流量的猛增与大幅度震荡，该模型预测稳定性较差。

表3 不同时间段的ERMS指标

2.2.2 流量误差对比

如图4所示，早7：00—9：00，KF 和BCM 预测流量误差波动性越来越大，BCM 的流量误差大体上在20以下，NPR 的流量误差则不超过20，且大多在10以内，说明了NPR 的适用性。

从图5可以看出，尽管平峰时客流的到达率会相对比较平均，KF 的流量误差仍很不平稳。BCM的流量误差则随时间趋于平稳，而且在平峰的后期，其流量误差是三类模型中最小的，所以BCM 更适用于预测短时流量少又平稳的时段。

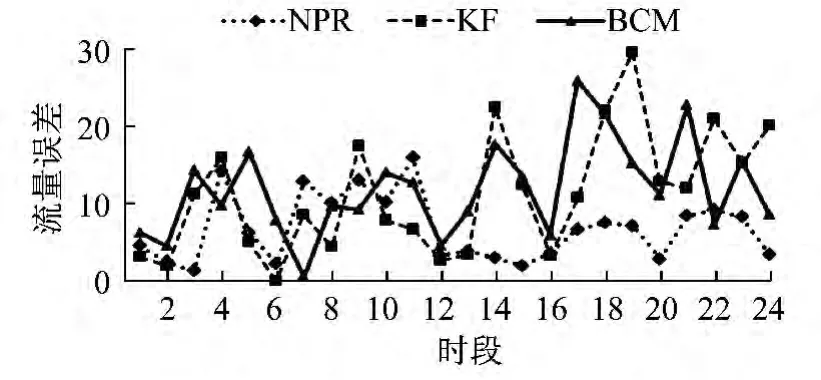
图4 早高峰流量误差

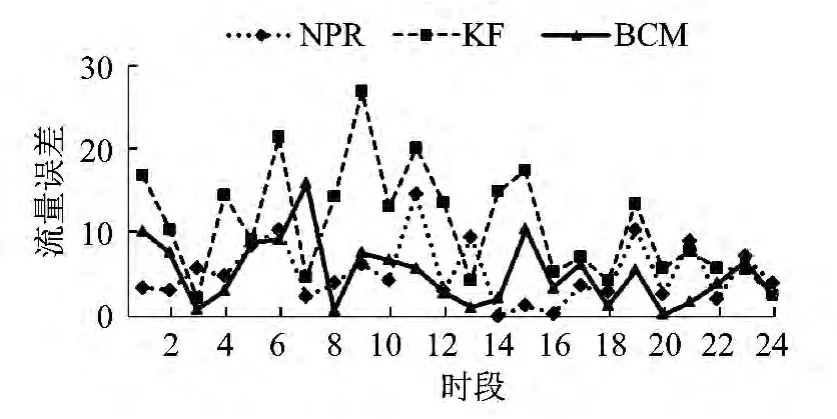
图5 平峰流量误差

如图6所示：晚高峰KF的误差明显大于NPR和BCM，甚至达到了80；BCM 的流量误差在NPR 和KF之间，说明BCM 融合了两个子模型的优点和缺点。计算贝叶斯权重就是为了中和预测精度，但这也决定了它不会比最优的子模型预测精度更高。

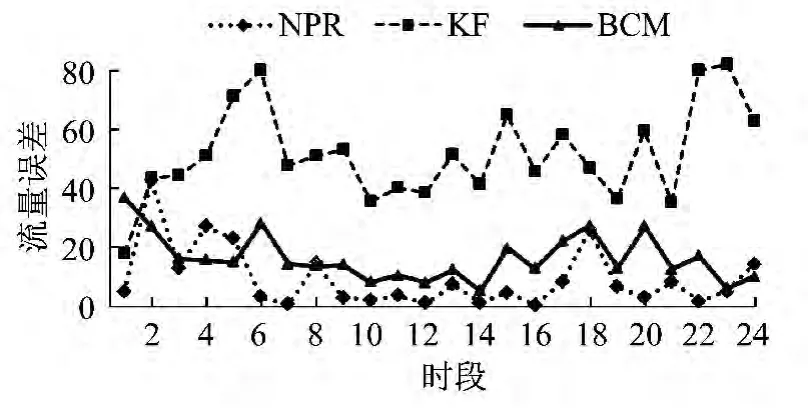
图6 晚高峰流量误差

3 结语

NPR 模型是基于历史数据的预测方法，没有固定的数学模型，应用条件是要有充足的、实时的观测数据，一般不少于一个月，其特点是预测精度依赖于数据量的大小。对于换乘站，如果有该线路相邻各站点的历史数据，可以真实且完整地表达客流状态的不同特征，从样本数据库中能够搜索到近邻点，就可以利用该模型得到精确的进站客流预测结果。而KF模型一般只需要预测站点一周的历史数据，没有其他的影响因素，所以同样可用于换乘站。

通过研究发现，NPR 模型的优点是应对突发事件的能力很强、预测准确性和误差分布较好，且不需要先验知识和大量的参数识别；但是其搜索速度较慢，参数调整也需要时间。KF 模型优点是算法简单，计算效率很高，对历史数据的需求量不大且应用广泛，但是其预测误差较大。在一天中不同时段的预测稳定性也不高，误差波动性大。BCM 模型是利用加权把多个单一预测模型线性组合起来，权值是根据每个子模型前一时期的预测误差计算条件概率得出的，其优点是提高了模型预测的稳定性。

进一步研究应尝试改进上述模型，使其精度和稳定性可以达到客流量实时预测的需求；另外可以探寻进站量、出站量、换乘量与断面客流量等参数之间的动态变化关系，从城市轨道交通客流形成机理方面构建新的预测模型。

［1］谢辉，董德存，欧冬秀，等.轨道交通短期客流预测方法及其算法研究［J］.现代城市轨道交通，2011（3）：96.

［2］毛静.城市轨道交通客流短期预测方法及实证研究［D］.北京：北京交通大学，2012.

［3］四兵锋，何九冉，任华玲，等.基于时序特征的城市轨道交通客流预测［J］.北京交通大学学报，2014，38（3）：1.

［4］董升伟.基于改进BP神经网络的轨道交通短时客流预测方法研究［D］.北京：北京交通大学，2013.

［5］Wei Y，Chen M C.Forecasting the short－term metro passenger flow with empirical mode decomposition and neural networks［J］.Transportation Research：Part C，2012，21（1）：148.

［6］邹巍，陆百川，邓捷，等.基于遗传算法与小波神经网络的客流预测研究［J］.武汉理工大学学报：交通科学与工程版，2014，38（5）：1148.

［7］Davis G，Nihan N.Nonparametric regression and short－term freeway traffic forecasting［J］.Journal of Transportation Engineering，1991，117（2）：178.

［8］宫晓燕，汤淑明.基于非参数回归的短时交通流量预测与事件检测综合算法［J］.中国公路学报，2003，16（1）：28.

［9］Clark S.Traffic prediction using multivariate nonparametric regression［J］.Journal of Transportation Engineering，2003，129（2）：161.

［10］翁剑成，荣建，任福田，等.基于非参数回归的快速路行程速度短期预测算法［J］.公路交通科技，2007，24（3）：93.

［11］Okutani I，Seephanedes Y J.Dynamic prediction of traffic volume through Kalman filtering theory［J］.Transportation Research Part B：Methodological，1984，18（1）：1.

［12］Hussein D.An object－oriented neural network approach to short－term traffic forecasting［J］.European Journal of Operational Research，2001（131）：253.

［13］Yin H，Wong S C，Xu J，et al.Urban traffic flow prediction using a fuzzy－neural approach［J］.Transportation Research C，2002，10（2）：85.

［14］Zheng W Z，Lee D，SHI Q X.Short－term freeway traffic flow prediction：Bayesian combined neural network approach［J］.Journal of Transportation Engineering，2006，132（2）：114.

［15］王奕，徐瑞华.基于周期时变特点的城市轨道交通短期客流预测研究［J］.城市轨道交通研究，2010（1）：46.