大面积带状区域高程拟合方法研究
2015-06-28黎峻宇刘立龙韦相任
黎峻宇,刘立龙,韦相任
(1.桂林理工大学广西矿冶与环境科学实验中心,广西 桂林 541004;2.桂林理工大学测绘地理信息学院,广西 桂林 541004;3.广西空间信息与测绘重点实验室,广西 桂林 541004;4.广东省有色金属地质局九三三队勘测公司,广东 肇庆 526060)
1 引 言
当前,GPS 测量技术已经在国家基础性建设中得到广泛应用。在这些基础设施中,铁路、公路、石油与燃气管道,水渠与排灌管道,电力设施中的输电线路,能源开发项目中的石油物探等等,往往集中在一些大面积的带状区域内[1]。GPS 测量直接获得的高程是相对于WGS-84 椭球面的大地高,实际生产过程中使用的却是相对于似大地水准面的正常高,如何直接利用GPS 大地高来获得满足工程需要的正常高,以便节省人力、物力和时间,一直是测量界关注和研究的一个重点,对大面积带状区域高程拟合方法的研究对国家基础性建设更是具有十分重要的现实意义。然而除了文献[1]等少数文献涉及带状高程拟合研究之外,鲜有人详细探讨涉及大面积带状区域的高程拟合方法。高程异常转换方法主要有四类:几何解析法、物理大地测量法、人工智能法和混合转换法,其中BP 神经网络、二次曲面拟合等方法在高程拟合中得到比较广泛的应用[2]。最小二乘支持向量机具有结构简单、全局最优,泛化能力较好的优点,能够很好地解决小样本、非线性、高维数、局部极小等问题,同时还克服了神经网络等一般学习机器中存在过学习、局部优化和样本数量要求多的弊端,基于以上原因文献[3][4]等开始将其应用到高程拟合中。本文使用一个大面积带状的GPS 网数据为基础,经最小二乘支持向量机、BP 神经网络、二次曲面拟合三种方法进行高程拟合,就不同方法拟合结果进行对比分析,获得一些具有一定价值的理论结果。最后根据这些理论结果,为国家基础性建设中大面积带状区域高程拟合提出一些实用性建议。
2 拟合方法
2.1 最小二乘支持向量机
最小二乘支持向量机原理是将最小二乘引入支持向量机中,采用等式约束代替不等式约束作为损失函数。训练过程由二次规划问题求解转化为线性方程组求解,同时使误差平方项达到最小化的计算过程[3]。设给定一个有M 个训练样本的集合(xi,yi),i=1,2…~M,其中训练m 维向量,xi∈Rm,输出数据yi∈R。按照结构风险最小化原则,函数拟合问题可转为下列函数的约束优化问题:

约束条件为:

式中:W∈Rm为权矢量;g(xi)是将x 从输入空间映射到特征空间的函数;ξi为误差项;C 为正规化参数,控制对超出误差样本的惩罚程度,b 为偏置量。
经过简化后得到最小二乘支持向量机函数为:

为了解决高维计算问题,引入一核函数K(xk,xj)来等效高维空间的内积形式[g(xk)g(xi)],即:

目前常用的核函数主要有多项式核函数K(x,x)=(x* y+1)p、径向基核函数(Radial Basis Function,RBF)K(x,x)=exp[-‖x-y‖2/(2σ2)]和Sigmoid核函数k(x,xi)=tanh[v(x* xi)+c]等形式。根据数值限制条件和参数较少以及优秀的局部逼近特征,本文选择RBF 作为支持向量机核函数。最小二乘支持向量机模型的确定最重要的是核函数参数σ 和正规化参数的选择,广泛采取的方法是试算法、交叉验证法、留一法[5]。我们输入的训练样本为三维向量,分别为高程点平面坐标和高程异常;输出向量只有一维,即高程异常;基于MATLAB 工具箱中最小二乘支持向量机自带的寻优函数进行参数寻优σ、C。
2.2 BP 神经网络
BP 神经网络是一个多层前向型神经网络,其权值调整采用误差反向传播算法,该网络由输入层、隐含层和输出层组成。设神经网络的输入向量为X=(X1,…,Xn)T,期望输出为d=(d1,…,dm)T,输入层与隐含层的权为W,其维数为n×s,阀值为θ1,维数为s×1,隐含层与输出层的权W',其维数为s×m,阀值为θ2,维数为m×1,其中n、s 和m 为别为输入层、隐含层和输出层的神经元节点数[6~7]。神经网络的正向传输的计算过程如下:
隐含层的输出计算公式为:

输出层的输出计算公式为:

上式中,f1(I1)、f2(I2)为隐含层与输出层的传递函数,f1(I1)通常为Sigmoid 函数。f2(I2)可以为Sigmoid 函数或Purelin 函数,y2为最终的输出值。
常用BP 神经网络通常采用误差反向传播法调整连接权。神经网络的目标函数为:

式中p 表示第p 个样本,k 表示第k 个节点,dk表示期望输出。
本文BP 神经网络在MATLAB 程序环境下建立,BP 神经网络构造各项内容如下:
(1)输入层神经元个数3 个,分别为高程点平面坐标和高程异常;
(2)输出层神经元个数1 个,即高程异常;
(3)训练函数取:tansig、purelin、trainlm.
(4)设置训练参数net.tranParam.show=100,net.tranParam.epochs=1000,net.tranParam.lr=0.01,net.tranParam.goal=1e-3,其他参数使用MATLAB 神经网络工具箱默认的取值。
2.3 二次曲面拟合
二次曲面拟合公式为:
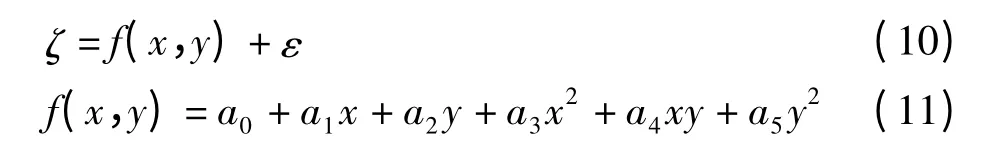
在(10)式中ξ 表示高程异常,(x,y)为已知点平面坐标,ε 是误差。在式(11)中有6 个参数,此时需要重合点不少于6 个。重合点个数多于6 个,采用最小二乘原理进行数学模拟,确定模型。
将式(11)写成矩阵形式:
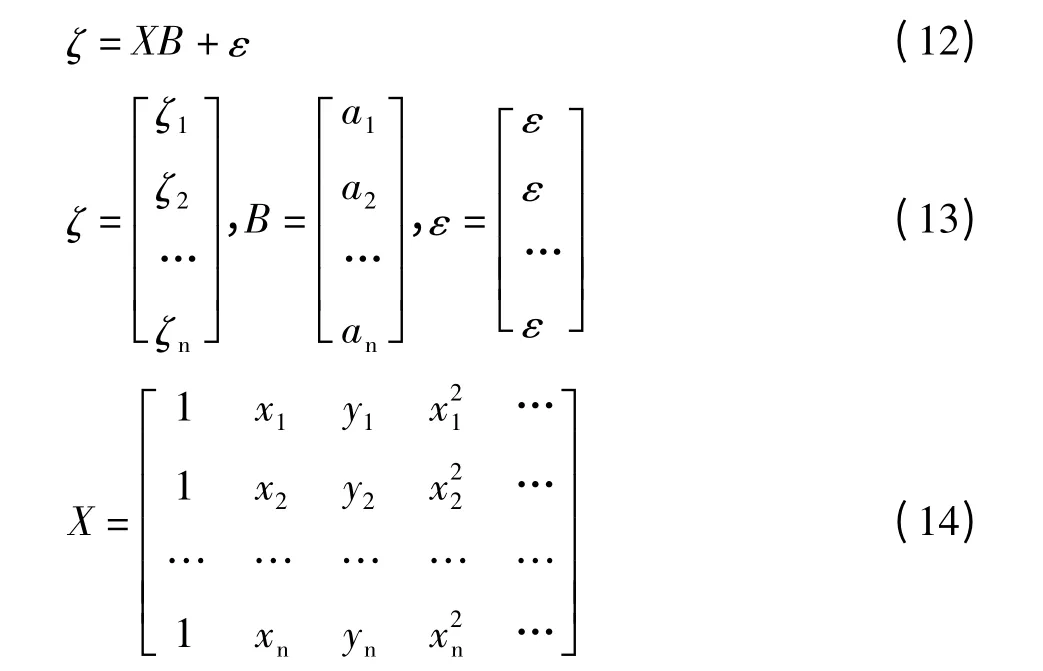
对每个重合点,都可以列以上方程,在∑ε2=min的条件下,解出ai,再通过式(11)求取未知点的ξ,从而解算得各点正常高。
3 实例分析
3.1 实例数据来源
本文采用某大型工程的D 级GPS 控制网点作为样本数据,该控制网共有点41 个,控制面积约为1 387.342 km2,控制网呈带状分布(点位分布如图1所示),水准按照二等水准测量要求施测。取33 个分布相对均匀的点作为样本点,8 个点作为拟合点。
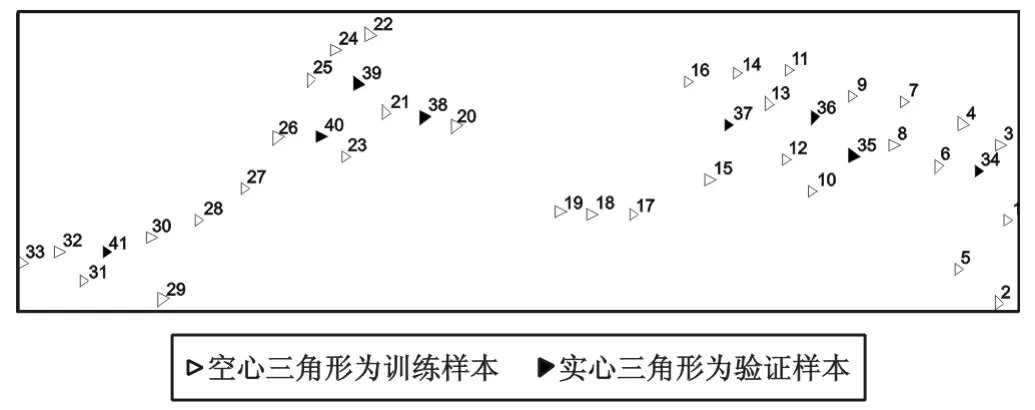
图1 点位分布图
3.2 各种方法拟合结果对比分析
为了验证不同模型的内符合精度,就拟合求取的样本点高程异常值与实测高程异常值之差进行统计,分析模型的可塑性。验证内符合精度的误差最大值(max)、误差最小值(min)、均方根误差(RMS)、平均绝对误差(MAE)见表1,不同方法在对应点拟合误差如图2 所示。

内符合精度对比 表1
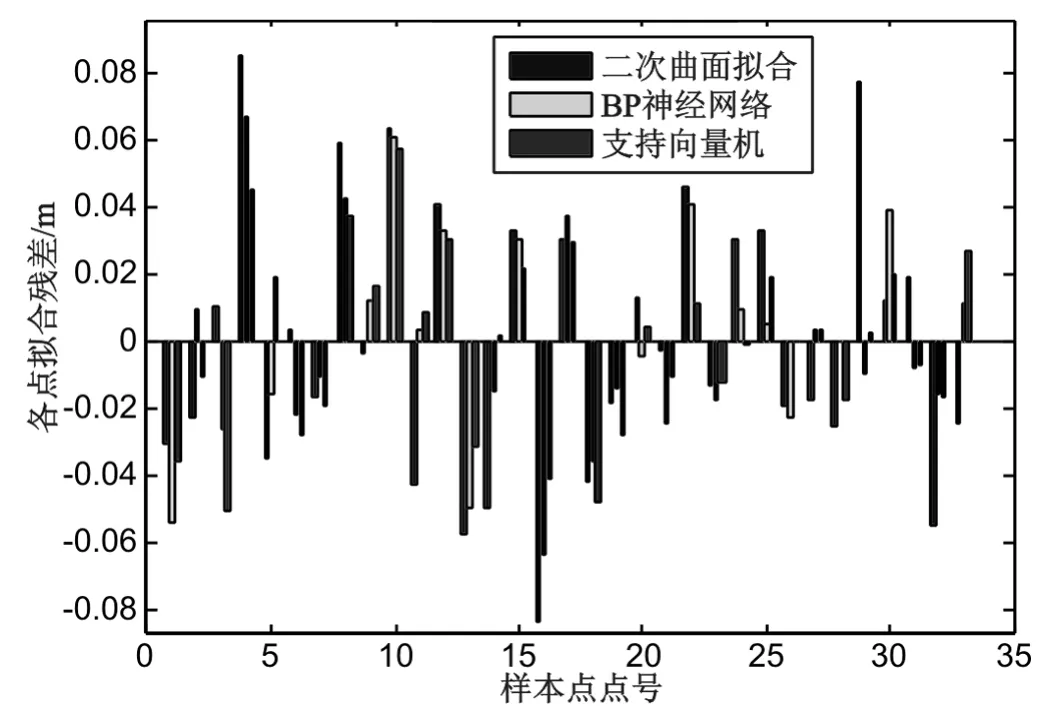
图2 样本点误差分布图
由表1、图2 知:支持向量机的误差最大值最小值之差在3 种方法中最小,MAE 最小,RMS 也最小;支持向量机与其他两种方法相比,进行高程拟合可以很好地控制较大的误差出现,同时支持向量机拟合误差变化范围更小,支持向量机拟合误差更好地控制在某一范围内;最小二乘支持向量机误差变化最小,内符合精度最高,相对其他的拟合方法提高了约1 cm,模型具有很好的可塑性;
验证模型的内符合精度只能达到分析模型可塑性的目的,为了充分说明各模型在大面积区域的泛化能力,还需要对模型的外符合精度进行验证。分析了各种方法在拟合点高程异常值与实测高程异常值之差,各种方法的max、min、RMS、MAE 如表2、图3 所示。

外符合精度对比 表2

图3 拟合点误差分布图
通过表2、图3 可以清晰地看到,支持向量机的误差最大值最小值之差在3 种方法中最小;3 种方法外符合精度比较接近,支持向量机MAE 比最小的BP 神经网络仅差1.9 mm,RMS 较最小的BP 神经网络也仅差1.3 mm;支持向量机与其他两种方法相比,进行高程拟合可以很好地控制较大的误差出现,最小二乘支持向量机误差变化较小,RMS 等于0.023 6 m,外符合精度可达cm 级精度,模型具有较好的泛化能力;
综上,对于本文所选实例区域,最小二乘支持向量机模型的内外符合精度可以达到厘米级精度,内符合精度为0.026 7 m,外符合精度为0.023 6 m,达到高程拟合的精度要求,可应用于大面积带状区域高程拟合。最小二乘支持向量机拟合模型同时获得较高的内外符合精度,具备较好的可塑性和泛化能力。
4 结 论
本文以大面积带状区域GPS 控制网为实验区域,使用最小二乘支持向量机、BP 神经网络、二次曲面拟合三种方法实施高程拟合,进行大面积带状区域高程拟合方法研究。通过探讨得出:
(1)最小二乘支持向量机可应用于大面积带状区域高程拟合,在本文大面积带状区域中拟合精度达到较理想的厘米级,且三种拟合方法的泛化能力很接近,BP 神经网络最强,最小二乘支持向量机次之。
(2)最小二乘支持向量机在大面积带状区域高程拟合中具有相当的优势,可同时获得较高的内外符合精度,该方法在可塑性优势明显的同时也具有较强的泛化能力。
(3)同一区域,不同方法拟合精度不同,本文试验获取数据具有局域性,不同的高程拟合方法在其他区域的适用性有待进一步验证。
综上所述,在大面积区域,进行高程拟合,建议可采用最小二乘支持向量机模型。
[1]高西峰.GPS 水准在带状区域似大地水准面精化中的应用研究[D].长安,长安大学,2007.
[2]任超,吴伟,黄征凯等人.基于ACI 准则的径向基函数网络在GPS 高程转换中的应用[J].测绘科学,2013(2):77~79.
[3]黄磊,张书毕,王亮亮等人.粒子群最小二乘支持向量机在GPS 高程拟合中的应用[J].测绘科学,2010(5):190~192.
[4]姬张建,袁运斌,盛传贞.混沌粒子群支持向量机并考虑地形改正的GPS 高程拟合[J].大地测量与地球动力学,2010(2):95~98.
[5]吴吉贤,杜海燕,张耀文.LSSVM 回归模型在局部区域GPS 高程拟合中的应用[J].测绘科学,2013(6):66~68.
[6]张德丰.MATLAB 神经网络应用设计[M].北京:机械工业出版社,2011:137~139.
[7]王小辉,王琪洁,丁元兰等人.基于二次曲面和BP 神经网络组合模型的GPS 高程异常拟合[J].大地测量与地球动力学,2012(6):103~106.
[8]张昊,王琪洁,朱建军等人.样本数据预处理对基于BP神经网络的高程转换的影响[J].大地测量与地球动力学,2011(2):125~128.
[9]邱卫宁.具有稳健初值的选权迭代法[J].武汉大学学报·信息科学版,2003(4):452~454.
[10]张恒璟,程鹏飞.基于GPS 高程时间序列粗差的抗差探测与插补研究[J].大地测量与地球动力学,2011(4):71~75.
