扭曲雅可比相交曲线上的斜-Frobenius映射

曹鸿钰,王鲲鹏

(中国科学院信息工程研究所,北京100093)

扭曲雅可比相交曲线上的斜-Frobenius映射

曹鸿钰,王鲲鹏

(中国科学院信息工程研究所,北京100093)

利用扭曲的雅可比相交曲线上的Frobenius自同态映射,构造在扭曲的雅可比相交曲线二次扭曲线上的一个斜-Frobenius映射,可用于制定扭曲的雅可比相交曲线的快速点乘算法,而不需要使用任何倍点。采用GLV方法加快扭曲的雅可比相交曲线上的点乘运算,给出斜的Frobenius映射的特征多项式。实例结果表明,该映射能够加速扭曲雅可比相交曲线上的标量乘运算。

雅可比相交曲线;双有理等价;扭曲曲线;斜-Frobenius映射;τ-展开;GLV方法

1 概述

早在1829年,Jacobi研究了雅可比相交(Jacobi intersection)形式的椭圆曲线(简称雅可比相交曲线),给出了其上的群律。雅可比相交曲线在1986年被Chudnovsky和Chudnovsky[1]引入椭圆曲线密码学。

雅可比相交曲线是一种三维空间中2个曲面的交,其上不仅可以有一般的标量乘,还可以实现配对计算。文献[2]给出了雅可比相交曲线上雅可比相交曲线上配对的具体计算方法。

本文回顾扭曲雅可比相交曲线和椭圆曲线上的Frobenius映射。介绍扭曲雅可比相交曲线上的Frobenius映射。引入斜-Frobenius映射,并应用Frobenius映射和斜-Frobenius映射来加速扭曲雅可比相交曲线上的的标量乘运算。

2 预备知识

2.1 背景介绍

雅可比相交曲线上的标量乘速度是比较有竞争力的,例如在其上可以进行快速倍点和三倍点计算。其中,文献[1]给出了射影坐标中雅可比相交曲线上的快速倍点和点加公式。文献[3-4]对快速倍点和点加公式给出了一些改进。文献[5]给出了雅可比相交曲线上的快速三倍点公式。文献[6]给出了更快速的公式。另外,文献[7]的分析表明特征3的域上雅可比相交曲线上的标量乘计算得更快。

由于计算Frobenius映射比计算倍点效率高,文献[8]提出了利用二次 twised椭圆曲线上的Frobenius映射替代倍点。文献[9]称这种映射为斜-Frobenius映射,并构造了亏格为2和3的超椭圆曲线上的斜-Frobenius映射。

文献[10]将雅可比相交曲线推广为扭曲雅可比相交形式的椭圆曲线(简称扭曲雅可比相交曲线)。在一个特征不为2的域k上,任一扭曲雅可比相交曲线双有理等价于一条椭圆曲线。利用扭曲雅可比相交曲线和椭圆曲线间的双有理映射,构造了域k上的扭曲雅可比相交曲线上的Frobenius映射,并给出这一Frobenius的特征方程。利用扭曲雅可比相交曲线上的Frobenius自同构映射可以构造快速标量乘算法。

利用扭曲雅可比相交曲线上的Frobenius映射和文献[8]中的方法,构造了扭曲雅可比相交曲线上的斜-Frobenius映射。借鉴文献[11]中的方法,结果表明斜-Frobenius映射可以用来加速扭曲雅可比相交曲线上的标量乘。扩展文献[12]的方法,文献[13]方法也可以应用在加速扭曲雅可比相交曲线的标量乘上。

2.2 雅可比相交曲线与扭曲雅可比相交曲线

特征不为2的域k上的雅可比相交曲线定义为:

其中,b∈k,(1-b)b≠0,(0,1,1)为零元。其上的群律由以下方程给出:

文献[10]将雅可比相交曲线推广为广义形式的扭曲雅可比相交曲线EJ,a,b,定义为:

其中,a,b∈k,(a-b)ab≠0。扭曲雅可比相交曲线的群律定义为[10]:

更加完整的群律可以参考文献[14]。

扭曲雅可比相交曲线是光滑曲线并且双有理等价于椭圆曲线y2=x(x-a)(x-b)。

一条扭曲雅可比相交曲线EJ,a,b是雅可比相交曲线EJ,1,b/a的二次扭曲曲线。 更一般地,EJ,a,b是的二次扭曲曲线,其中。反过来,每个扭曲雅可比相交曲线的二次twist曲线是一个扭曲雅可比相交曲线。

2.3 椭圆曲线上的Frobenius映射

设Fq是一个特征大于2的有限域。Fq上的椭圆曲线定义为:

其中,∞ 为无穷远点。椭圆曲线E上的q次Frobenius映射πq定义为:

记N=#E(Fq),根据Hasse定理得到N=q+1-t,这里,且πq的特征方程aq(λ)为:

3 Frobenius映射

设Fq是一个特征大于2的有限域且EJ,a,b是定义在Fq的扭曲雅可比相交曲线。考虑如下的EJ,a,b上的q次Frobenius映射:

并且证明如下结论。

定理1EJ,a,b是定义在Fq上的扭曲雅可比相交曲线且#EJ,a,b=q+1-t。那么对于任一P∈EJ,a,b(Fq),EJ,a,b上的Frobenius映射Πq满足:

为了证明这一定理,引入如下的引理。

引理1Fq是一个特征大于2的有限域。任意一个Fq上的扭曲雅可比相交曲线在Fq中双有理等价于一个形式为y2=x(x-a)(x-b)的椭圆曲线[10]。

根据引理1,存在Fq上的一个形式为y2=x(xa)(x-b)的椭圆曲线E,满足设ψ是EJ,a,b到E的同构映射,φ是ψ的逆映射。由文献[10]中的定理3.2,得到映射:

是EJ,a,b到E双有理等价映射,同时它的逆映射φ为:

点(u,v,w)=(0,1,1)对应点(x,y)=∞,点(u,v,w)=(0,1,-1)对应点(x,y)=(b,0)。

引理2EJ,a,b是定义在Fq上的扭曲雅可比相交曲线且E是形式为y2=x(x-a)(x-b)的椭圆曲线。设#E(Fq)=q+1-t,ψ是如上定义的双有理映射,πq是E上的q次Frobenius映射。定义Ψ=ψ-1° πq°ψ,那么:

(1)Ψ∈End(EJ,a,b)(即 Ψ 是EJ,a,b上的同源映射);

(2)任一P∈EJ,a,b(Fq),Ψ满足:

证明:根据对引理1的讨论,ψ是EJ,a,b到E的Fq中的同构映射,πq是E上到自身的Fq中的同源映射。根据Ψ的定义,Ψ是EJ,a,b到自身的Fq中的同源映射。

对于任一P∈EJ,a,b(Fq),记Q=ψ(P)∈E(Fq),则:

根据文献[15]的定理4.8得到:

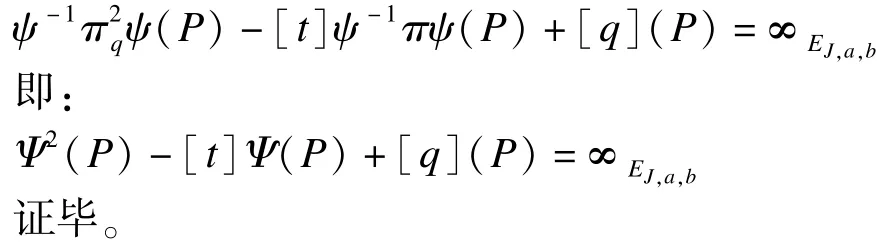
定理1的证明:E是Fq上的一个形式为y2=x(x-a)(x-b)的椭圆曲线,Ψ是引理2中的EJ,a,b自同构映射。根据 Ψ 的定义,对于任一P=,有:

可以用这样的Frobenius映射加速扭曲雅可比相交曲线上的标量乘。

4 斜-Frobenius映射

利用第3节中的扭曲雅可比相交曲线上的Frobenius映射构造雅可比相交曲线的二次twist曲线上的斜-Frobenius映射。这个构造是文献[8,11]中结果的扩展。

Fq上的EJ,a,b是的二次扭曲曲线,其中,满足,令:

其中,α=。若α是k=Fq上的二次非剩余,则映射ϕ是在域上的EJ,a,b到的同构映射,记的二次twist曲线为

定理2EJ,a,b是k=Fq上的扭曲雅可比相交曲线且是EJ,a,b的二次扭曲曲线。设#EJ,a,b(Fq)=q+1-t,映射ϕ是上的到的同构映射。设Πq是EJ,a,b上的q次Frobenius映射。定义,则对于任一满足:

和 Frobenius映射 Πq类似,上 的 斜-Frobenius映射可以用来加速扭曲雅可比相交曲线上的标量乘。

5 方法应用描述与实例

为了加速标量乘,文献[16-17]利用Frobenius自同构映射开发出了不利用倍点公式的标量乘算法。这种基于Frobenius自同构的特征方程的nP分解已经被用来计算标量乘:

其中,ci是固定集合中的元素,例如{-q/2,…,q/2}。

若Fq是一个小域时,标量乘可以使用不相邻形式以τ为基展开nP来加速[18-19]。当Fq非常大时,文献[13]设计了一种方法来加速标量乘。

5.1 τ-进制展开方法

EJ,a,b是k=Fq上的扭曲雅可比相交曲线且EJ,a,b是EJ,a,b的二次扭曲曲线。根据定理 2,存在一个复数τ使得上的斜-Frobenius映射可以被认为是τ。τ是一个由以下方程给出的复数:

其中,t=q+1-#EJ,a,b(Fq)。可以将k∈Z[τ]的ω宽窗口τ的不相邻形式(ω-τNAF)表示如下:

其中,ci∈{-q/2,…,q/2},i=0,1,…,t-1;如果ci,ci+1,…,ci+ω-1是ω个连续系数,那么它们当中至多一个非零。

利用EJ,a,b上的Frobenius映射Πq,上述方法可以应用在扭曲雅可比相交曲线上。

5.2 GLV方法

扩展文献[11]的方法,将GLV方法应用在扭曲雅可比相交曲线的标量乘上。

定理3设Fq的特征大于3,EJ,a,b是k=Fq上的扭曲雅可比相交曲线,且#EJ,a,b(Fq)=q+1-t。令是上的EJ,a,b的二次扭曲曲线,则设是一个素数且r＞2q。ϕ:是一个定义在上的扭曲同构映射。令:

则对于任一P∈Et J;a;满足:

由于r是素数且r＞2q,因此根据定理假设,可以得到,但是。这意味着若,则属于,那么就存在λ∈Z满足

例1p=2192-264-1是一个素数。d=264+1是Fp上的一个二次非剩余。则在上,EJ,1,λ(λ=-421)的二次扭曲曲线是。 在上,EJ,1,λ到的扭曲同构映射定义为:

由于d是Fp上的一个二次非剩余且p≡ 1(mod4),因此在上对于任一满足

例2p=2255-19是一个素数。d=121 665/ 121 666是Fp上的一个二次非剩余,则是EJ,-1,λ(λ=-5 737)在上的二次扭曲曲线。可以定义EJ,1,λ到的上的扭曲同构映射为:

d是Fp上的一个二次非剩余且p≡1(mod4),则在

同时由于EJ,a,b是的二次扭曲曲线,其中这样可以选小一点的,使得是EJ,a,b的二次扭曲曲线。

6 结束语

本文论述了定义在有限域Fq上的扭曲雅可比相交曲线中的自同构,介绍了扭曲雅可比相交曲线上Frobenius映射的性质并给出了这个Frobenius映射的特征方程。应用扭曲雅可比相交曲线上的Frobenius映射,构造了定义在扭曲雅可比相交曲线二次扭曲曲线上的斜-Frobenius映射。结果表明,扭曲雅可比相交曲线的Frobenius映射和斜-Frobenius映射可以加速扭曲雅可比相交曲线上的标量乘运算。

[1] Chudnovsky D V,Chudnovsky G V.Sequencesof Numbers Generated by Addition in Formal Groups and New Primality and Factorization Tests[J].Advances in Applied Mathematics,1986,7(4):385-434.

[2] 唐春明,徐茂智,亓延峰.Jacobi交上的配对计算[J].计算机工程与科学,2011,33(10):25-29.

[3] Liardet P Y,Smart N P.Preventing SPA/DPA in ECC Systems Using the Jacobi Form[C]//Proceedings of the 3rd International Workshop on Cryptographic Hardware and Embedded Systems.Berlin,Germany:Springer, 2001:391-401.

[4] Bernstein D J,Lange T.Explicit-formulae Database [EB/OL].(2008-03-12).http://www.hyperelliptic. org/EFD.

[5] Hisil H,CarterG,DawsonE.New Formulaefor Efficient Elliptic Curve Arithmetic[C]//Proceedings of the 8th International Conference on Cryptology in India. Berlin,Germany:Springer,2007:138-151.

[6] Hisil H,Wong K K H,Carter G,et al.Faster Group Operations on Elliptic Curves[C]//Proceedings of the 7th Australasian Conference on Information Security. [S.l.]:Australian Computer Society Inc.,2009:7-20.

[7] 端木庆峰,张雄伟,王衍波,等.3特征域椭圆曲线群点的快速计算算法[J].解放军理工大学学报:自然科学版,2011,12(1):1-6.

[8] Iijima T,Matsuo K,Chao J,et al.Construction of Frobenius Maps ofTwistsEllipticCurvesand Its Application to Elliptic Scalar Multiplication[C]// Proceedings of Conference on Small Computer System Interface.Berlin,Germany:Springer,2002:699-702.

[9] Kozaki S,Matsuo K,Shimbara Y.Skew-Frobenius Maps on Hyperelliptic Curves[J].IEICE Transactions on Fundamentals of Electronics,Communications and Computer Sciences,2008,91(7):1839-1843.

[10] Feng Rongquan,Nie Menglong,Wu Hongfeng.Twisted Jacobi Intersections Curves[J].Theoretical Computer Science,2013,494:24-35.

[11] Wang Mingqiang,Wang Xiaoyun,Zhan Tao,et al. Skew-Frobenius Map on Twisted Edwards Curve[C]// Proceedings of the 7th International Conference on Theory and Application of Models of Computation. Prague,Czech:[s.n.],2010:199-210.

[12] Gallant R P,Lambert R J,Vanstone S A.Faster Point Multiplication on Elliptic Curves with Efficient Endomorphisms[C]//Advances in Cryptology-CRYPTO’01.Berlin,Germany:Springer,2001:190-200.

[13] Galbraith S D,Lin X,Scott M.Endomorphisms for Faster Elliptic Curve Cryptography on a Large Class of Curves[J].Journal of Cryptology,2011,24(3): 446-469.

[14] Wu H,Feng R.A Complete Set of Addition Laws for Twisted Jacobi Intersection Curves[J].Wuhan University Journal of Natural Sciences,2011,16(5): 435-438.

[15] Silverman J H.The Arithmetic of Elliptic Curves[M]. Dordrecht,the Netherlands:Springer,2009.

[16] Solinas J A.Efficient Arithmetic on Koblitz Curves[J]. Designs,Codes and Cryptography,2000,19(2/3): 195-249.

[17] Solinas J A.An Improved Algorithm for Arithmetic on a Family of Elliptic Curves[C]//Proceedings of CRYPTO’97.Berlin,Germany:Springer,1997:357-371.

[18] Koblitz N. CM-curves with Good Cryptographic Properties[C]//Proceedings of CRYPTO’91.Berlin, Germany:Springer,1992:279-287.

[19] Blake I F,KumarM V,Xu Guangwu.Efficient Algorithms for Koblitz Curves over Fields of Characteristic Three[J].Journal of Discrete Algorithms, 2005,3(1):113-124.

编辑 顾逸斐

Skew-Frobenius Mapping on Twisted Jacobi Intersection Curve

CAO Hongyu,WANG Kunpeng
(Institute of Information Engineering,Chinese Academy of Sciences,Beijing 100093,China)

Using the Frobenius endomorphism on twisted Jacobi intersection curve,this paper constructs a skew-Frobenius mapping which is defined on the quadratic twist of twisted Jacobi intersection curve.It can be exploited to devise fast point multiplication algorithm on twisted Jacobi intersection curve that does not use any point doubling.The Gallant-Lamber-Vanstone(GLV)method can be used for speeding up point multiplication on twisted Jacobi intersection curve.The characteristic polynomial of the mapping is given.Example results show that the mapping can speed up the scalar multiplication of twisted Jacobi intersection curve.

Jacobi intersection curve;birationally equivalent;twist curve;skew-Frobenius mapping;τ-expansion; Gallant-Lamber-Vanstone(GLV)method

1000-3428(2015)01-0270-05

A

TP391

10.3969/j.issn.1000-3428.2015.01.051

国家“973”计划基金资助项目(2013CB338001);国家自然科学基金资助项目(61272040);中国科学院战略性先导科技专项基金资助项目(XDA06010702)。

曹鸿钰(1988-),男,硕士研究生,主研方向:信息安全;王鲲鹏,教授。

2014-02-18

2014-03-20 E-mail:feng_896@163.com

中文引用格式:曹鸿钰,王鲲鹏.扭曲雅可比相交曲线上的斜-Frobenius映射[J].计算机工程,2015,41(1):270-274.

英文引用格式:Cao Hongyu,Wang Kunpeng.Skew-Frobenius Mapping on Twisted Jacobi Intersection Curve[J]. Computer Engineering,2015,41(1):270-274.