基于双索引的子图查询算法
2015-06-27陆慧琳
陆慧琳,黄 博
(复旦大学计算机科学与技术学院智能信息处理重点实验室,上海200433)
基于双索引的子图查询算法
陆慧琳,黄 博
(复旦大学计算机科学与技术学院智能信息处理重点实验室,上海200433)
传统的子图查询算法大多只在图数据库上进行一次挖掘算法,即在图数据库上建立稳定的数据库索引后将不再对索引进行更新。随着查询兴趣的改变或数据库的频繁更新,原有的数据库索引将不再能提供有用的信息来减少查询过程中候选图的数量。为此,提出一种双索引的子图查询算法,同时在数据库和查询流上挖掘频繁子图并建立索引。子图查询和查询流索引的建立同步进行,即使查询兴趣改变,查询流索引也能自适应地更新索引信息来优化查询效率。针对数据库的频繁更新,查询流索引已提供实时的有效信息,数据库索引无需重新建立。实验结果表明,双索引的结合能有效提高查询子图的处理效率。
双索引;查询流索引;子图查询;频繁子图;图数据库;子图同构
1 概述
图作为一种通用的数据结构可以用来表示各种复杂的数据,被广泛地应用于各个领域,包括化学、生物信息[1]、软件工程、社交网络以及互联网[2]等。而对于图数据库的管理与传统的数据库有许多的不同,其中基于图数据库的查询有着明显的区别。查询匹配过程中重要的一环工作是子图同构检测,但是同构检测本身是NP问题[3]。为了降低花费在子图同构检测上的时间,可以通过建立有效的索引来减少查询过程中候选图的数量,从而缩短整个子图查询所需的时间。
文献[4]是最早针对子图查询问题的研究,它提出以路径为特征建立索引;文献[5]提出采用树形结构+部分图结构作为索引;文献[6]同样采用了树+部分图,不过它采用了一种基于哈希值的指纹技术;文献[7]采用了两步挖掘方法,先用深度优先生成子树,再用广度优先扩展成子图;文献[8-9]都采用了频繁子图作为索引特征,前者使用差别率函数保留那些过滤能力较强的子图,后者将所有频繁子图分别存储在内存和硬盘中。
传统的子图搜索算法大多只在图数据库上建立索引,本文采取双索引的方法,同时在图数据库和查询流上建立索引。在子图查询的过程中,挖掘在查询流中的频繁子图,实时地建立查询流索引作为数据库索引的补充,反映实时的用户查询兴趣。在查询流索引的建立过程中,利用数据库索引以及查询的结果集减小建立索引的代价。在应对数据库的频繁更新时,并不采用重新挖掘整个数据库的方法,而是根据用户需求将查询流索引中的重要索引图更新到数据库索引中。
2 基本概念
2.1 相关定义
定义1(图) 一个图G可由一组五元组(V,E,LV,LE,l)表示。其中,V表示图中结点的集合;E是图中边的集合;LV,LE分别表示图中结点和边标号的集合;l是标号映射函数,定义了V→LV和E→LE的映射关系。
定义2(子图同构) 有2个图G1(V1,E1,LV1,LE1,l1)和G2(V2,E2,LV2,LE2,l2),如果存在一个单射函数f∶V1→V2,使得:
(1)∀u∈V1,l1(u)=l2(f(u));
(2)∀(u,v)∈E1,l1(u,v)=l2(f(u),f(v))成立,那么G1和G2是子图同构的,G1是G2的同构子图。
定义3(支持集、支持度) 给定一个图数据库GD={g1,g2,…,gn},一个子图g的支持集为:
SSg={g′∈GD|g是g′的同构子图}
支持度为:
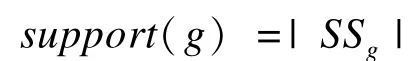
定义4(候选集、必要集) 给定一个图g,它的候选集CSg、必要集ESg和支持集SSg之间的关系为:
必要集ESg⊆支持集SSg⊆候选集CSg
2.2 问题描述
本文要解决的问题是:给出一串查询流QS={q1,q2,…,qn,…},在图数据库GD={g1,g2,…,gn}中进行子图匹配查询,返回每个查询qx的结果集:
RSqx={g∈GD|qx是g的同构子图}
3 子图查询算法
本文算法最大的特点是双索引结构。传统的子图搜索方法大多只在数据库上建立索引,并且单独地处理每个查询。而本文利用查询之间可能存在的相似性,在查询流上动态地建立查询流索引,与数据库索引结合成为基于双索引的子图查询方法。本文的双索引都是基于频繁子图,且索引指向的都是数据库中的图。
图1为本文算法的子图查询流程:查询流中的一个查询q进入处理窗口;在枚举q的子图过程中,依次与数据库索引和查询流索引进行匹配过滤;同时,记录在此过程中涉及到的查询流子图;过滤后的候选集再进行同构检测,得到查询q的结果集;查询q的结果集作为涉及到的查询流子图的必要集更新到查询流索引中,同时,达到频繁条件的查询流索引图将计算其支持集。
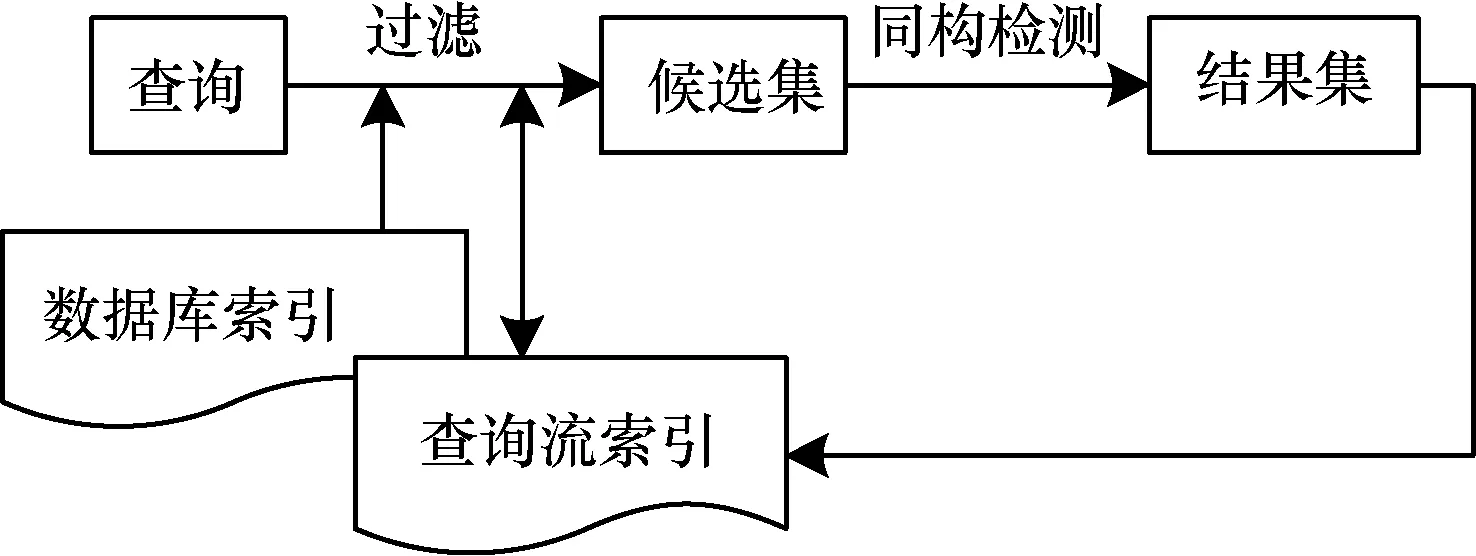
图1 子图查询算法总流程
3.1 数据库索引
定义5(数据库频繁子图) 给定一个图数据库GD={g1,g2,…,gn},且给定一个频繁系数δd,如果一个子图g在图数据库GD中的支持度support(g)≥δd×|GDg|,那么则称子图g为数据库频繁子图。
频繁子图的概念是相对的,一个图是否频繁取决于频繁系数δd的设定。
3.1.1 索引结构
本文采用类似于经典的gSpan[10]频繁子图挖掘算法对图数据库进行候选图的生成与挖掘。图2是由一个图数据库生成的部分候选图,图标号右边的数字表示的是子图在数据库中的支持度。

图2 数据库频繁子图的候选图
采用树形结构对频繁子图进行管理。图3是基于图2中的候选图建立的数据库索引树。树中,每个结点表示一个候选图;在第LX层的子图有X条边;树的根结点为空集;L0层的图只有一个结点,没有边;一个结点的孩子结点是它扩展一条边后的超图。
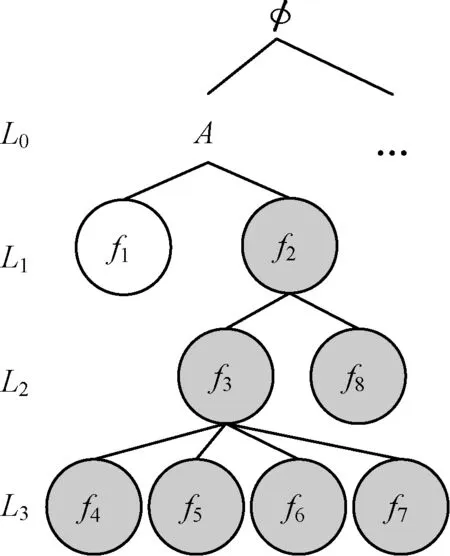
图3 数据库索引树
在本文的例子中,图数据库的大小为1 000,如果频繁系数δd定义为0.3,那么图3中灰色结点为频繁子图,这些频繁子图将被最终编入数据库索引;白色结点为非频繁子图,将被直接剪枝。下一小节将具体说明索引树的建立过程。
3.1.2 索引建立
确定频繁系数δd后,开始对图数据库GD进行数据库索引的建立:
(1)标号映射。把数据库中图的结点标号和边标号按出现频率升序排序,出现频次小于δd×|GDg|的结点和边可以直接从枚举过程中排除(因为包含这些结点或者边的子图肯定不是频繁子图),其余标号按出现频率升序映射到一个字典序。这样做的优点在于:在挖掘过程中对非频繁子图能更早地剪枝;且同一子图在进行支持集计算时能大量减少同构检测次数。
(2)按字典序。对只有一个结点的图(L0层)建立以其为树根的索引树。
(3)边扩展。按DFS码[10]递增的顺序,将当前子图进行边扩展。比如,在本文的例子中,图2中的图f1为结点A扩展一条标号为a的边生成的子图(采用DFS码递增的方法可以大量避免同一个图的重复枚举。详细见文献[10])。
(4)支持度计算。在计算扩展子图f的支持度时,并不需要对整个数据库图进行同构检测,扩展子图父结点的支持集就是f的候选集。比如在计算图3中候选图f3的支持集时,它的候选集就是f2的支持集。
如果当前扩展子图f是频繁子图,则将其加入数据库索引树,并且以子图f为当前子图回到算法第(3)步。
如果当前扩展子图f不是频繁子图,则直接将其剪枝,因为它的超图也不可能是频繁的。接下来以扩展子图f的父结点为当前结点回到算法第(3)步。
(5)当所有以单结点图(L0层)为根的树建立完成后,算法结束。
3.1.3 具体实现
在具体的实现中,本文采用哈希表来帮助快速定位树中的频繁子图以及它们的支持集。图结构本身很难进行直接哈希,此处再次利用了DFS码。每个频繁子图可以转换成一个由字符串表示的最小DFS码,比如图 2中f4的最小 DFS码为: 01AaB02AaB03AaB。除了以上提到的快速定位,使用DFS码的优点还在于:
(1)在频繁子图挖掘过程中,可以避免枚举子图的遗漏和重复。
(2)当需要检测两个图是否相同时,只需进行简单的字符串匹配,而不是时间开销很大的同构检测。
3.2 查询流索引
在建立查询流索之前,先要明确查询流索引中频繁子图的定义。查询流中频繁的概念与数据库并不相同,那是因为数据库是静态的,而查询流是源源不断的动态变化着。一个子图在数据库中是否频繁非常明确:support(g)≥δd|GDg|(定义5),但是查询流的大小|QS|一直在增长,显然查询流不能像数据库那样定义频繁子图。这里引入一个时间窗的概念。笼统地讲,用户只对当前时间窗内的查询流感兴趣,而频繁子图的概念也相对于当前时间窗口内的查询流。
定义6(历史支持度、当前支持度) 给定一个查询流QS={q1,q2,…,qn,…}和一个时间窗口大小window_size,当前查询为qn。
一个查询流索引中的结点f的历史支持度为:
support_hisf=|{qi∈QS|f是qi的同构子图,且(⌊n/window_size」-1)×window_size<i≤⌊n/ window_size」×window_size|
f的当前支持度为:
support_curf=|{qi∈QS|f是qi的同构子图,且⌊n/window_size」×window_size<i≤n}|+support_hisf
定义7(查询流频繁子图) 给定时间窗口大小window_size和查询流频繁系数δq,如果一个查询流索引中的结点f的当前支持度support_curf≥δq×window_size,那么f被称为查询流频繁子图。
从定义7注意到,当前支持度中包含了历史支持度。在理想状态下,希望记录一个子图f在时间窗口内精确的支持度。但为了精确,必须记录下f在查询流中每次出现的查询序列号,空间消耗较大。所以本文给出了当前支持度的近似定义。
除了频繁子图的定义不同,查询流索引的另一个重要问题是其动态增长性。查询流持续不断地进入处理窗口,相应的查询流索引也会越来越大。为了控制查询流索引的规模,引入了时间戳的概念。
定义8(时间戳) 假设查询流QS={q1,q2,…,qn,…},1,2,…,n,…,为每个查询的序列号。查询流索引中的每个结点S都有一个时间戳timeS,其值为最后一次出现在查询流中的查询序列号。
在每个时间窗口结束时,扫描整个查询流索引,将时间戳小于当前窗口的结点删除。
3.2.1 索引结构
数据库索引中存储的都是频繁子图,但查询流索引中存储的不仅仅是频繁子图,也存储那些将来可能会变成频繁的子图。这些潜在频繁子图并没有准确地计算出支持集,而在将来某一刻它变成频繁子图时,需要借助它的子图的支持集来作为它的候选集进行支持集计算。而已知支持集的子图越多,需要进行同构检测的候选集就越小。所以,在查询流索引中很有必要记录它与多个子图的包含关系。
另外,在查询流中频繁的子图也有可能在数据库中是频繁的。为了减少重复的计算和存储,以及充分地利用数据库索引中的信息,采取数据库索引和查询流索引信息共享的数据结构。
图4是一个查询流索引的示例,图中圆形结点为数据库索引中的频繁子图(图3);方形结点为查询流索引中的子图,其中灰色结点为频繁子图且已经计算出支持集;白色结点为非频繁子图;图中连接方形结点的虚线表示2个结点的子图同构关系。从图中可以看到与数据库索引的区别:索引中的每个结点会有不止一个父亲结点。这样设计的好处在于可以缩小索引图的候选集大小。比如图中f2达到频繁子图条件时,其候选集CSf′2=SSf′1∩SSf′2,父结点越多,候选集越小。
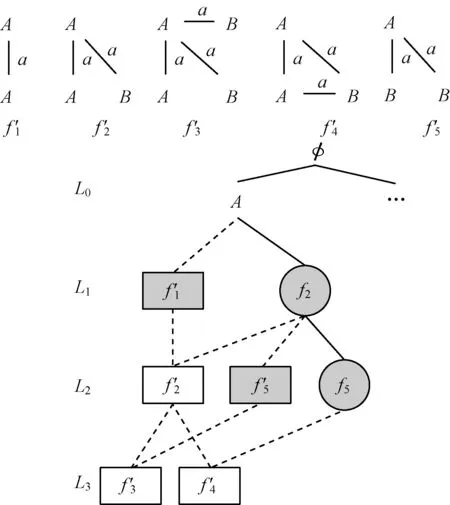
图4 查询流索引
3.2.2 索引建立与子图查询
查询流索引的建立与子图查询的处理过程是互相交织在一起的。处理查询的大致步骤为:枚举,过滤和验证:
(1)枚举查询q的所有边长小于Lmax的子图集SD,与数据库索引和查询流索引进行匹配,匹配的结果有4种:
1)子图在数据库索引中(子集SD1);
2)子图在查询流索引中,且已经是频繁子图(子集SD2);
3)子图在查询流索引中,但还没有达到频繁的条件,则将其当前支持度加1(子集SD3);
4)子图既不在数据库索引也不在查询流索引中,则将其添加到查询流索引中,当前支持度为1 (子集SD4)。
(2)把子图集 SD中的所有频繁子图(SD1+SD2)的支持集作交,作为查询q的候选集。
(3)在候选集上进行子图同构检测,得到查询q的结果集。
(4)查询q的结果集作为子图集SD中部分子图(SD3+SD4)的必要集,更新到查询流索引中。如果SD中有子图达到查询流频繁的条件,则计算其支持集。
(5)定期扫描查询流索引,删除超出时间窗外的子图,防止查询流索引的无休止增长。
图5、图6是一个包括了查询流索引更新的子图查询示例。查询q进入处理窗口后,对其进行子图枚举(图5中q.0~q.5),得到的匹配结果为:
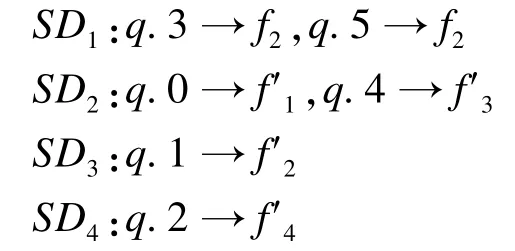
得到查询q的候选集为:

在CSq上进行同构检测后,得到查询q的结构集RSq。将RSq作为SD3和SD4中子图的必要集更新到数据库中。
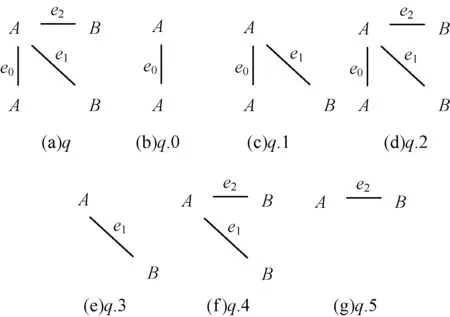
图5 查询q及其枚举子图
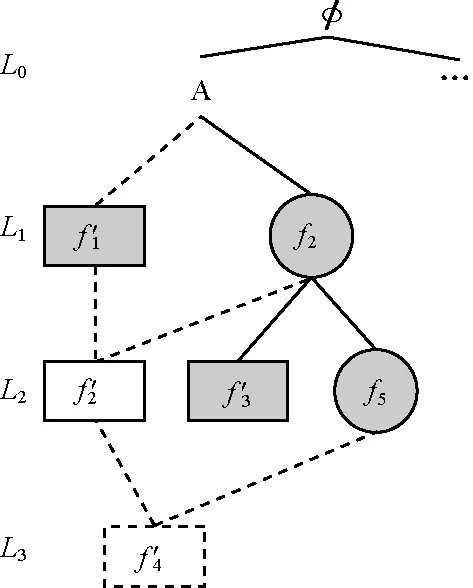
图6 处理查询q后更新的双索引结构
4 实验结果与分析
本文将与2个经典的子图搜索算法FG-Index[9]和GCoding[11]进行实验比较,以验证本文算法的可行性。实验环境为Intel i5 2.5 GHz CPU,8 GB内存,64位Linux系统。
本文采用的实验集为生物领域的AIDS数据库,该数据库包含1万个分子图。实验中的查询流是根据AIDS数据库随机生成,按边数(4,8,12,16,20)等比例生成后进行混合。在实验中,查询流按查询个数分为1 000~6 000。数据库频繁系数δd为0.1;查询流频繁系数δq为0.01;最大频繁子图边数Lmax为4;时间窗口window_size为500。
图7显示了平均查询时间随着查询流大小增加的变化曲线。从实验结果可看出,本文算法相较于传统算法具有以下优势:随着查询流中所含查询数量的增加,查询之间的相似性被充分挖掘,查询流索引中存储了更多有用的信息,平均的查询时间开销就会随之降低。
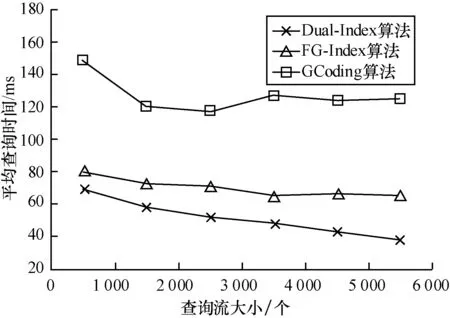
图7 平均查询时间随查询流大小的变化曲线
图8显示了平均候选集大小随着查询流大小增加的变化曲线。这里的候选集大小是以同构检测的次数来计量。从图中可以看到:在查询流较小时,候选集大小相对较大。其主要原因在于:在建立查询流索引的过程中,进行了查询流频繁子图的支持集计算,其中包含了大量同构检测计算。这在查询流较小时,会产生额外的同构检测次数。但随着查询流的增大,处理查询前期建立的查询流索引为后来的查询提供了大量的有用信息,降低了平均的候选集大小。
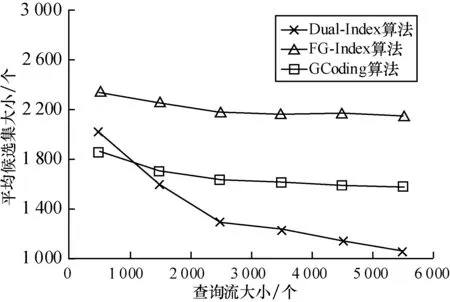
图8 平均候选集大小随查询流大小的变化曲线
5 结束语
本文提出一种基于双索引的子图搜索算法,相较于传统算法,本文算法引入了查询流索引,采用时间窗的概念定义了查询流频繁子图,时间窗的概念不仅控制了索引的规模也实时地反映了查询兴趣。在子图查询过程中,提高了总的查询效率。下一步的研究方向将着重于查询流索引的优化,减少查询流索引产生的额外空间开销,提高挖掘出的查询流频繁子图的质量,加速查询流索引的建立。
[1] 彭佳扬,杨路明,王建新,等.一种高效挖掘生物网络闭合频繁子图的算法[J].高技术通讯,2009,19(2): 188-193.
[2] 楼宇波,马 坚,周皓峰,等.基于频繁链接的Web权威资源挖掘[J].计算机研究与发展,2003,40(7):1095-1103.
[3] Johnson D S,Garey M R.Computers and Intractability: A Guide to the Theory of Np-completeness[M]. [S.1.]:W.H.Freeman and Company,1979.
[4] Giugno R,Shasha D.GraphGrep:A Fast and Universal Method for Querying Graphs[C]//Proceedings of ICPR’02.Quebec,Canada:IEEE Press,2002:123-129.
[5] Zhao Peixiang,Yu J X,Yu P S.Graph Indexing:Tree+delta>=graph[C]//Proceedings of VLDB’2007. [S.1.]:IEEE Press,2007:233-241.
[6] Klein K,Kriege N,Mutzel P.CT-Index:Fingerprint-based Graph Indexing Combining Cycles and Trees[C]// Proceedings of ICDE’11.Hannover,Germany:IEEE Press, 2011:258-265.
[7] 李先通,李建中,高 宏.一种高效频繁子图挖掘算法[J].软件学报,2007,18(10):2469-2480.
[8] Yan Xifeng,Yu P S,Han Jiawei.Graph Indexing:A Frequent Structure-based Approach[C]//Proceedings of SIGMOD’04.Paris,France:ACM Press,2004:568-576.
[9] Cheng J,Ke Y,Ng A,et al.FG-index:Towards Verification-free Query Processing on Graph Data-bases[C]//Proceedings of SIGMOD’07.Beijing,China:[s.n.],2007: 541-549.
[10] Yan Xifeng,Han Jiawei.gSpan:Graph-based Substructure Pattern Mining[C]//Proceedings of ICDM’02.Maebashi, Japan:IEEE Press,2002:236-246.
[11] Zou Lei,Chen Lei,Xu J,et al.A Novel Spectral Coding in A LargeGraph Database[C]//Proceedingsof EDBT’08.Nantes,France:ACM Press,2008:321-329.
编辑 索书志
Subgraph Query Algorithm Based on Dual Index
LU Huilin,HUANG Bo
(Key Lab of Intelligent Information Processing,School of Computer Science,Fudan University,Shanghai 200433,China)
Most traditional subgraph query algorithms only conduct a mine-at-once algorithm on the graph database. That is,after establishing a stable database index,the index is no longer be updated.This kind of algorithms may encounter such problems:with the query interest frequently changing or the database frequently updating,the original database index becomes increasingly obsolete and no longer provides useful information to effectively reduce the number of candidate graphs.Based on this consideration,this paper proposes a dual index structure which mines frequent subgraphs on the database and the query stream,and establishes index on them.The process of subgraph query and the establishment of query index are simultaneous.They complement each other.So even if the query interest changes,the query stream index can be adaptively updated to optimize the query performance.For the frequent updates of database,the database index doesnot need to be re-built,because the query stream index provides useful information in real time. Experimental results show that the dual index improves the processing efficiency of subgraph query.
dual index;query stream index;subgraph query;frequent subgraph;graph database;subgraph isomorphism
1000-3428(2015)01-0044-05
A
TP391
10.3969/j.issn.1000-3428.2015.01.008
陆慧琳(1988-),女,硕士研究生,主研方向:数据库技术,数据挖掘;黄 博,硕士。
2014-03-05
2014-04-03 E-mail:luhuilin@fudan.edu.cn
中文引用格式:陆慧琳,黄 博.基于双索引的子图查询算法[J].计算机工程,2015,41(1):44-48.
英文引用格式:Lu Huilin,Huang Bo.Subgraph Query Algorithm Based on Dual Index[J].Computer Engineering,2015, 41(1):44-48.
