基于高分辨率反演谱分解的储层流体流度计算方法研究

张生强,韩立国,李 才,闫 涛,王玉秀,麻旭刚

(1.中海石油(中国)有限公司天津分公司,天津300452;2.吉林大学地球探测科学与技术学院,吉林长春130026)

基于高分辨率反演谱分解的储层流体流度计算方法研究

张生强1,韩立国2,李 才1,闫 涛1,王玉秀1,麻旭刚1

(1.中海石油(中国)有限公司天津分公司,天津300452;2.吉林大学地球探测科学与技术学院,吉林长春130026)

反射地震数据中的低频信息包含了与储层及流体有关的丰富信息，从地震数据中提取储层流体流度属性可以为利用地震低频信息进行储层预测和流体识别提供一种新的途径。为此，研究并提出了基于高分辨率稀疏反演谱分解的储层流体流度计算方法。首先基于Biot孔隙介质依赖频率的反射系数低频渐近分析理论，推导出了储层流体流度属性的计算表达式；然后利用地震数据低频段优势频率的瞬时谱振幅代替相应频率处的反射系数，给出了储层流体流度属性的直接近似计算方法，其中关于瞬时谱的计算采用了基于交替方向算法的高分辨率稀疏反演谱分解方法，该方法相对于常规谱分解方法具有更高的时间分辨率和频率分辨率。陆上和海上二维叠后地震资料的试处理结果表明，基于高分辨率稀疏反演谱分解的储层流体流度计算方法得到的储层流体流度属性剖面分辨率非常高，对于含油气储层显示了良好的成像能力，降低了储层流体识别的多解性和不确定性。

储层流体识别；流体流度；反演谱分解；交替方向法；低频信息

反射地震数据中的低频信息包含了与储层及流体有关的丰富信息，对于地震储层预测和油气检测非常重要[1]。Silin等[1-5]对Biot模型含流体孔隙介质分界面的地震反射信息进行了低频渐近分析，通过引入一个小的无量纲参数进行推导，得到了依赖频率的含流体孔隙介质的反射系数渐近表达式，该反射系数正比于流体流度、地震信号的频率和流体密度三者乘积的平方根。同时，Silin等[1-5]预测纵波反射系数在低频端达到峰值。基于Biot孔隙介质模型的低频渐近分析理论可应用于地震正演、反演以及属性分析等方面。由于储层流体流度的大小变化可以引起烃饱和储层介质的速度频散变化[6]，因此可以利用储层流体流度属性进行储层预测和流体检测。

Korneev等[7]利用低频渐近分析理论对储层产油率进行了地震成像。Goloshubin等[8]在低频渐近分析理论的基础上提出了成像属性的概念(其正比于流体流度的平方根)，将井的产油率与流体流度联系起来，并研究了成像属性在含油气储层成像、预测产油率和区分油藏油水界面中的作用。Goloshubin等[9]进一步根据低频渐近分析理论进行地震属性分析，估计储层渗透率。Goloshubin等[10]使用低频渐近分析理论尝试对气藏下方产生的低频阴影进行解释。蔡涵鹏[11]在低频渐近分析理论的基础上对成像属性的计算、流体流度属性计算、渗透率与成像属性的关系、成像属性与油气生产率的关系以及优势频率的确定方法进行了系统研究，并用实际数据进行了试算。Chen等[12-13]在低频渐近分析理论基础上，利用地震低频信息和广义S变换方法推导了计算储层流体流度的方法，并使用该方法处理了实际地震资料，取得了一定的效果。

由此可见，从地震数据的低频信息中提取储层流体流度属性可以为利用地震低频信息进行储层预测和流体识别提供一种新的途径，具有重要的研究意义。然而，现有的关于储层流体流度的计算方法都存在相同的缺点，即分辨率比较低。针对该问题，本文应用Biot模型孔隙介质依赖频率的反射系数低频渐近分析理论，推导出基于高分辨率稀疏反演谱分解的储层流体流度计算方法，并进一步测试了利用储层流体流度属性进行储层预测和流体识别的效果。实际资料处理结果表明，该方法计算得到的储层流体流度信息分辨率非常高，对于含油气储层显示了良好的成像能力。

1 方法原理

1.1 储层流体流度的计算

Silin等[5]对Biot孔隙弹性介质模型进行了低频渐近分析，取得了一系列成果：①在低频范围内获得了有效的渐近简谐波解；②在平面纵波入射到渗透地层界面的情况下，获得了反射系数和透射系数相对简单的显式表达式；③获得了来自渗透地层的快纵波反射共振频率的显式表达式。本文主要根据渗透地层的快纵波反射共振频率表达式和流体饱和孔隙介质在低频域中的地震反射系数渐近表达式推导储层流体流度的计算表达式。

Silin等[5]推导的渗透地层的快纵波反射共振频率表达式为：

(1)

Silin等[5]推导的流体饱和孔隙介质在低频域中的地震反射系数渐近表达式可表示为[7]：

(2)

式中：R0和R1是实系数，它们是岩石和孔隙流体的力学特性(包括密度、孔隙度和弹性系数)的无量纲函数；i是虚数单位；ω是地震信号的角频率；ρf是储层的流体密度。从(2)式可以看出：含流体孔隙介质储层依赖频率的地震反射系数R正比于储层流体流度、孔隙流体密度和地震信号频率三者乘积的平方根。

在渗透力学中，储层的流体流度F被定义为储层的渗透率与流体的粘滞系数之比，即F=κ/η。从(2)式可知，地震反射系数R是储层流体流度F,地震信号的角频率ω和流体密度ρf的复函数。所以，为了从地震数据中提取流体流度属性信息，利用(2)式对频率求导，即：

(3)

(4)

式中，系数C是岩石骨架和孔隙流体的弹性性质以及地震信号角频率的复函数，可通过测井数据估算[8]。

由(4)式可得储层流体流度属性的计算表达式

(5)

从(5)式可知，储层流体流度与反射系数对频率的一阶导数的平方成正比。对地震信号进行时频分解后，其单频瞬时谱振幅或能量能够准确刻画该频率的地震反射振幅或能量。所以，在实际应用计算中，我们用频率为ω的瞬时谱振幅a(ω)代替相应频率处的反射系数R，则有

(6)

由于相对于传统的时频分析方法，即Gabor变换、连续小波变换(CWT)、S变换(或广义S变换)等，基于稀疏反演的谱分解方法具有更高的分辨率和更好的聚焦性[14]，所以本文采用基于稀疏反演的谱分解方法计算(6)式中的a(ω)。在理论计算中，还需要利用(1)式确定计算储层流体流度的优势频率ω。Silin等[1,5]指出，当岩石和孔隙流体的特性在合理范围时，依赖频率的地震反射系数在地震低频端达到峰值，这个结论与在实际数据中观测到的低频阴影一致[8,15-18]。因此，我们根据(6)式使用地震信号的低频成分计算储层的流体流度属性是合理的。

(6)式将储层流体流度表示为抛物线函数的形式。所以，在有已知井的产能或渗透率参数的情况下，利用各井处计算得到的[∂a(ω)/∂ω]2，即可通过抛物线拟合求得参数C。而在勘探区内少井或无井的情况下，由于C相当于一个比例系数，仍可在不依赖井的情况下直接计算[∂a(ω)/∂ω]2来获取储层流体流度的相对值[12-13]。

1.2 基于稀疏反演的谱分解方法

反演谱分解的主要思想是[19]：首先将谱分解描述为一个线性反演问题，然后使用稀疏反演算法求解该线性反演问题，从而得到一个稀疏的时频谱。反演谱分解可以作为一个基追踪问题或基追踪去噪问题[20]来求解。

1.2.1 反演谱分解的数学模型

非平稳地震褶积模型[14]表达式为

(7)

式中：s(t)表示地震记录；wi(t)表示以下角标i对应的频率为主频的子波；ri(t)表示与wi(t)对应的依赖频率的反射系数；N表示参与计算的反射系数或子波向量的数量；n(t)表示随机噪声，“*”代表褶积运算。

(7)式的物理意义是指地震记录s(t)是由一系列不同频率的子波wi(t)和与之对应的依赖频率的地层伪反射系数(这里ri(t)称为伪反射系数是为了区别于真实的地下介质反射系数)ri(t)褶积后相加，再加上随机噪声n(t)组成的。根据线性代数理论，可以将(7)式写成矩阵与向量相乘的形式：

(8)

或

b=Ax+n

(9)

式中：s=b表示地震记录；Wi表示子波wi(t)对应的褶积矩阵；A=(W1W2…WN)代表子波褶积矩阵库；x=(r1r2…rN)T代表依赖频率的地层伪反射系数矩阵。

由(9)式可知，当已知子波褶积矩阵库A和地震记录b时，便可以通过求解线性反演问题得到依赖频率的伪反射系数矩阵x。数据矩阵(r1r2…rN)的行和列分别代表时间和频率，所以将x转化为(r1r2…rN)的形式，即可以认为是反演得到的时频谱。通常在地球物理反演中，由(9)式定义的反演谱分解问题是一个欠定问题，为了降低问题(9)的不确定性和多解性，得到稀疏的时频谱，需要对时频谱x进行稀疏约束，进而将问题(9)转化为基追踪去噪问题，即：

(10)

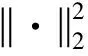
1.2.2 交替方向优化算法

最近几年，学者们发展了多种求解基追踪去噪问题的快速算法，如谱投影梯度法(Spectral Projected Gradient，简称SPGL1)[21]、快速迭代软阈值法(Fast Iterative Shrinkage-Thresholding Algorithm，简称FISTA)[22]、分块坐标梯度下降法(Block Coordinate Gradient Descent，简称为CGD)[23]和交替方向法(Alternating Direction Method，简称ADM)[24]等。相对于SPGL1，FISTA和CGD等算法，Yang等[24]证明了ADM算法是一种高效、稳健的重构算法，具有更好的数值计算性能。因此，本文采用ADM算法求解无约束基追踪去噪问题(10)，实现反演谱分解。

应用ADM算法求解问题(10)时，首先要引入辅助变量r∈Cm，将问题(10)转换为如下等价形式：

(11)

(11)式的增广Lagrangian子问题为：

(12)

式中：Re(·)表示对复数取实部运算；y∈Cm是Lagrangian乘子；H表示共轭转置运算；罚参数β>0。如果给定(xk,yk)，则可以通过求解交替极小化问题(12)的方法得到(rk+1,xk+1,yk+1)。求解原始问题(10)的ADM算法迭代框架如下[24]：

(13)

式中：Shrink(·,·)表示一维收缩算子；gkAH·(Axk+rk+1-b-yk/β)；γ>0是一常数；τ>0是近端参数(proximal parameter)。

以上所述算法即为ADM算法，该算法具有很好的数值计算性能，并且适合处理复数，所以适用于稀疏反演谱分解。

1.2.3 合成地震数据测试分析

图1a是由不同频率Ricker子波合成的地震信号，用于测试谱分解方法。第1个子波的中心时间为50ms，0相位，主频为60Hz；第2个子波的中心时间为150ms，-90°相位，主频为40Hz；第3个子波是由相同子波中心时间(270ms)、相同相位(-180°)、不同频率(20Hz和60Hz)的两个子波组成的；第4个子波是由两个中心时间间隔很短(间隔40ms)的子波构成的，其中一个子波中心时间为380ms，0度相位，主频为30Hz，另一个子波中心时间为420ms，0度相位，主频为30Hz。图1b 为图1a所示合成地震信号的理论时频谱，图1c 展示的是CWT时频谱，图1d展示的是S变换时频谱，图1e展示的是基于ADM算法的稀疏反演时频谱。

对比图1给出的3种谱分解方法所得结果可以看出：相对于常规谱分解方法CWT(图1c)和S变换方法(图1d)，基于ADM算法的反演谱分解方法(图1e)具有更高的时间分辨率和频率分辨率，可以分辨出多频率成份重叠的两个子波(第3个子波)及时间间隔很近的两个子波(第4个子波)；而常规谱分解方法受时频分辨率相互制约的限制很难将其分开。

图1 合成地震信号及其基于ADM算法的稀疏反演谱分解与常规谱分解方法所得结果对比

2 实际地震数据试处理

将本文提出的基于高分辨率反演谱分解的储层流体流度计算方法分别应用于陆上和海上二维实际地震数据试处理，以验证该方法在储层预测及流体识别中的有效性。

2.1 陆上地震数据试处理

首先应用储层流体流度属性检测陆上实际地震数据的含气储层。图2为某地区陆上二维实际地震数据的叠后剖面，图中红色箭头指示的是目标储层位置，该目标储层已经被勘探井证实是含气储层。经频谱分析可知该叠后地震数据的主频在45Hz左右。

分别采用基于CWT谱分解和基于高分辨率稀疏反演谱分解的储层流体流度计算方法处理图2 对应的实际地震数据，得到的储层流体流度属性剖面(红色表示强能量异常)分别如图3和图4所示。

图2 某地区陆上二维实际地震数据叠后剖面

图3 陆上二维地震数据基于CWT谱分解的储层流体流度计算方法得到的储层流体流度剖面

图4 陆上二维地震数据基于高分辨率稀疏反演谱分解的储层流体流度计算方法得到的储层流体流度剖面

从图3和图4中可以看到，含气目标储层在各自的储层流体流度属性剖面中均显示为明显的强能量异常(红色箭头标注)。通过对比可以看出，基于高分辨率稀疏反演谱分解方法计算得到的储层流体流度属性剖面(图4)具有更高的分辨率和可识别性，背景干扰较少。同时，相对于图2所示的叠后地震剖面，基于高分辨率稀疏反演谱分解方法计算得到的储层流体流度属性剖面能够更好地反映含气储层的展布。

2.2 海上地震数据试处理

图5为某海区过井A和井B的实际地震数据叠后剖面，黄色虚线标记的是目标储层位置，绿色椭圆标注的是有效目标储层位置，该目标储层已经被勘探井证实是含油储层。井A在有效目标储层位置钻遇油层，而井B在目标储层位置处钻遇到水层。经频谱分析可知，该叠后地震数据的主频约为55Hz。

分别采用基于CWT谱分解和基于高分辨率稀疏反演谱分解的储层流体流度计算方法处理图5 对应的实际地震数据，得到的储层流体流度属性剖面(红色表示强能量异常)分别如图6和图7所示。

从图6和图7中可以看到，井A处含油目标储层在两种方法计算的储层流体流度属性剖面中都同样显示为明显的强能量异常(绿色椭圆标注)，而在井B处的目标储层段无能量异常特征。与陆上地震数据的处理结果类似，基于高分辨率稀疏反演谱分解方法计算得到的储层流体流度属性剖面同样具有更高的分辨率和可识别性，背景干扰少，且检测结果与钻井结果完全吻合。同时，相对于图5 所示的叠后地震剖面，基于高分辨率稀疏反演谱分解方法计算得到的流体流度属性剖面能够更好地反映含油储层的分布。

图5 某海区过井A和井B的二维实际地震数据叠后剖面

图6 海上二维地震数据基于CWT谱分解的储层流体流度计算方法得到的储层流体流度剖面

图7 海上二维地震数据基于高分辨率稀疏反演谱分解的储层流体流度计算方法得到的储层流体流度剖面

3 结束语

本文应用含流体孔隙介质依赖频率的反射系数渐近分析理论，推导出了基于高分辨率稀疏反演谱分解的储层流体流度计算方法。使用该方法计算得到的储层流体流度信息对于含油气储层具有良好的成像能力，且分辨率很高，为利用地震资料的低频信息进行储层预测和流体识别提供了一种新的途径。同时，该方法同样适用于无井的情况(特别是海上油气勘探)，通过将流体流度计算公式中的比例系数C设定为某一常数，计算的储层相对流体流度可以用来进行储层流体的定性分析。

需要指出的是，由于储层流体流度属性的计算基于地震数据的低频信息，所以在地震数据采集到处理的整个过程中都要注意保留地震信号的低频成分，以提高所提取储层流体流度属性信息的可靠性。

[1] Silin D B,Korneev V A,Goloshubin G M,et al.A hydrologic view on Biot’s theory of poroelasticity[R].Berkeley:Lawrence Berkeley National Laboratory,2004:1-23

[2] Silin D B,Korneev V A,Goloshubin G M,et al.Low-frequency asymptotic analysis of seismic reflection from a fluid-saturated medium[J].Transport in Porous Media,2006,62(3):283-305

[3] Silin D,Goloshubin G.Seismic wave reflection from a permeable layer:low-frequency asymptotic analysis[C]∥ASME 2008 International Mechanical Engineering Congress and Exposition.Boston：American Society of Mechanical Engineers，2008:47-56

[4] Silin D.A low-frequency asymptotic model of seismic reflection from a high-permeability layer[R].Berkeley:Lawrence Berkeley National Laboratory,2009:1-28

[5] Silin D,Goloshubin G.An asymptotic model of seismic reflection from a permeable layer[J].Transport in Porous Media,2010,83(1):233-256

[6] Batzle M L,Han D H,Hofmann R.Fluid mobility and frequency-dependent seismic velocity-direct measurements[J].Geophysics,2006,71(1):N1-N9

[7] Korneev V A,Silin D,Goloshubin G M,et al.Seismic imaging of oil production rate[J].Expanded Abstracts of 74thAnnual Internat SEG Mtg,2004,1476-1479

[8] Goloshubin G,van Schuyver C,Korneev V,et al.Reservoir imaging using low frequencies of seismic reflections[J].The Leading Edge,2006,25(5):527-531

[9] Goloshubin G,Silin D,Vingalov V,et al.Reservoir permeability from seismic attribute analysis[J].The Leading Edge,2008,27(3):376-381

[10] Goloshubin G,Chabyshova E.A possible explanation of low frequency shadows beneath gas reservoirs[J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012,1-5

[11] 蔡涵鹏.基于地震资料低频信息的储层流体识别[D].成都:成都理工大学,2012 Cai H P.Reservoir fluid identification from low-frequency seismic wave[D].Chengdu:Chengdu University of Technology,2012

[12] Chen X H,He Z H,Zhu S X,et al.Seismic low-frequency-based calculation of reservoir fluid mobility and its applications[J].Applied Geophysics,2012,9(3):326-332

[13] Chen X H,He Z H,Pei X G,et al.Numerical simulation of frequency-dependent seismic response and gas reservoir delineation in turbidites:a case study from China[J].Journal of Applied Geophysics,2013,94(4):22-30

[14] 韩利.高分辨率全谱分解方法研究[D].长春:吉林大学,2013 Han L.Research on the methods of high-resolution full spectrum decomposition[D].Changchun:Jilin University,2013

[15] Castagna J P,Sun S,Siegfried R W.Instantaneous spectral analysis:detection of low-frequency shadows associated with hydrocarbons[J].The Leading Edge,2003,22(2):120-127

[16] Liu J,Marfurt K J.Instantaneous spectral attributes to detect channels[J].Geophysics,2007,72(2):P23-P31

[17] Sinha S,Routh P S,Anno P D,et al.Spectral decomposition of seismic data with continuous-wavelet transform[J].Geophysics,2005,70(6):P19-P25

[18] Wang Y.Seismic time-frequency spectral decomposition by matching pursuit[J].Geophysics,2007,72(1):V13-V20

[19] Portniaguine O,Castagna J.Inverse spectral decomposition[J].Expanded Abstracts of 74thAnnual Internat SEG Mtg,2004,1786-1789

[20] Chen S S,Donoho D L,Saunders M A.Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing,1998,20(1):33-61

[21] Van Den Berg E,Friedlander M P.Probing the Pareto frontier for basis pursuit solutions[J].SIAM Journal on Scientific Computing,2008,30(2):890-912

[22] Beck A,Teboulle M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J].SIAM Journal on Imaging Sciences,2009,2(1):183-202

[23] Yun S,Toh K C.A coordinate gradient descent method for L1-regularized convex minimization[J].Computational Optimization and Applications,2011,48(2):273-307

[24] Yang J F,Zhang Y.Alternating direction algorithms for L1-problems in compressive sensing[J].SIAM Journal on Scientific Computing,2011,33(1):250-278

(编辑：戴春秋)

Computation method for reservoir fluid mobility based on high-resolution inversion spectral decomposition

Zhang Shengqiang1,Han Liguo2,Li Cai1,Yan Tao1,Wang Yuxiu1,Ma Xugang1

(1.TianjinBranchofCNOOCLtd.,Tianjin300452,China;2.CollegeofGeo-ExplorationScienceandTechnology,JilinUniversity,Changchun130026,China)

The low-frequency information of seismic reflection data contains abundant information related to reservoir and fluid.Extracting reservoir fluid mobility property from seismic data provides a new means for reservoir prediction and fluid recognition.Therefore,we study and propose a calculation method of reservoir fluid mobility based on high resolution inversion spectral decomposition.Firstly,the computation formula for reservoir fluid mobility is deduced based on asymptotic analysis theory of frequency-dependent reflection coefficient in saturate porous medium of Biot model.Then,the instantaneous spectral amplitude of the dominant frequency at low frequency replaces its reflection coefficient,and the direct approximate calculation method for reservoir fluid mobility is derived.It is emphasized that the related instantaneous spectrum is calculated by using the high resolution sparse inversion spectral decomposition based on alternating direction algorithm,which has higher time-resolution and frequency-resolution than the conventional spectral decomposition method.Finally,the reservoir fluid mobility calculation method is applied to process the land and marine post-stack seismic data.The actual data processing results show that the reservoir fluid mobility section based on high-resolution sparse inversion spectral decomposition has high-resolution and well imaging capability to oil and gas reservoir,which reduces the multi-solutions and uncertainty of reservoir fluid identification.

reservoir fluid identification,fluid mobility,inverse spectral decomposition,alternating direction method (ADM),low-frequency information

2014-04-27;改回日期：2014-10-12。

张生强(1987—)，男，博士研究生，助理工程师，主要从事储层预测、地震资料综合解释方面的研究。

国家科技重大专项(2011ZX05025-001-07)资助。

P631

A

1000-1441(2015)02-0142-08

10.3969/j.issn.1000-1441.2015.02.004