基于多尺度加窗希尔伯特变换的地震资料体边缘检测

李 斌,陈学华,贺振华,许 迪,李依佳,裴小刚,唐湘蓉

(1.成都理工大学油气藏地质及开发工程国家重点实验室,四川成都610059;2.成都理工大学地球探测与信息技术教育部重点实验室,四川成都610059)

基于多尺度加窗希尔伯特变换的地震资料体边缘检测

李 斌1,2,陈学华1,2,贺振华1,2,许 迪2,李依佳2,裴小刚2,唐湘蓉2

(1.成都理工大学油气藏地质及开发工程国家重点实验室,四川成都610059;2.成都理工大学地球探测与信息技术教育部重点实验室,四川成都610059)

利用地震资料识别断层或裂缝发育带等非连续性异常信息是裂缝性油气藏储层预测的关键所在。为此,提出了一种基于多尺度加窗希尔伯特变换的体边缘检测新方法。在二维(水平)加窗希尔伯特变换的基础上,考虑了非连续性地质异常的多尺度三维特征,通过同时调节水平和深度方向上的计算孔径来提取实际三维地质异常体的边缘信息,弥补了二维加窗希尔伯特变换仅提取水平方向边缘信息的明显不足。实际地震资料体边缘检测试处理结果表明,该方法能够完整地刻画多尺度非连续性地质异常体的特征,有效突出裂缝发育带的边缘位置及断层的走向,具有较为显著的实用价值。

体边缘检测;广义希尔伯特变换;多尺度特征;水平孔径;深度孔径

勘探实践表明,含油气储层裂缝发育非常普遍,而大量空隙或裂缝组成的边缘特征信息是可检测的。传统的边缘检测方法,如利用Robert算子、Sobel算子、Canny算子等的微分法和拟合法等,由于其计算简单、定位精度高等特点,已被应用于同相轴追踪[1]。随着可视化和图像处理技术的发展,源于图像和信号分析领域的边缘检测技术也在地震裂缝检测中获得了广泛的应用[2]。如Bahorich等[3]1995年提出的地震相干数据体分析技术；贺振华等[4]1999年提出的基于地下介质横向变化的地震多尺度边缘检测技术。2001年,Robert[5]首次将曲率作为一种地震属性应用到地震资料解释中,给出了层面属性的定义和计算方法,此为第一代曲率属性;2003年,Luo等[6]提出了一种广义希尔伯特变换(Generalized Hilbert Transform,GHT),并将其应用于地震资料中河道信息的成像;党志敏等[7]分析了GHT在含噪信号边缘检测中的应用效果;陈学华等[8]于2011年提出基于广义S变换的分频裂缝边缘检测方法。

由于傅里叶变换是一种全局性变换,不能有效突出非平稳信号的局部特征[9-10]；而图像是二维非平稳信号,建立在傅里叶变换基础上的传统希尔伯特变换虽然具有唯一性,可以检测到图像边缘信息,但在高精度和多尺度方面不能得到满意的结果。三维地震资料中断层或裂缝发育带等不连续信息在内部结构上存在复杂多样性,在空间上存在多尺度特征,如果仅考虑二维(水平)加窗希尔伯特变换,则难以同时刻画地质异常在水平和深度方向上的多尺度特征,无法给出其完整的地质信息[11]。

为此,本文提出一种基于时间域多尺度加窗希尔伯特变换的体边缘检测新方法,将二维(水平)加窗边缘检测拓展到三维(体)加窗边缘检测,同时在水平和深度方向上采用不同的孔径计算地质异常体边缘信息,突出不同尺度下不连续性信息的完整异常特征。实际地震资料的体边缘检测试处理结果证明了新方法的有效性。

1 方法原理及实现流程

1.1 加窗希尔伯特变换的基本原理

希尔伯特变换是一种全通滤波器,原始信号经过希尔伯特变换后可以得到相应的解析信号。对于离散信号x(t),希尔伯特变换的滤波过程可以表述为:

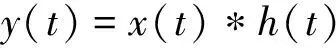
(1)

式中:x(t)为输入信号;y(t)为希尔伯特变换后的输出信号;h(t)为滤波因子。

因此,时间域的希尔伯特变换可表示为一个褶积关系：

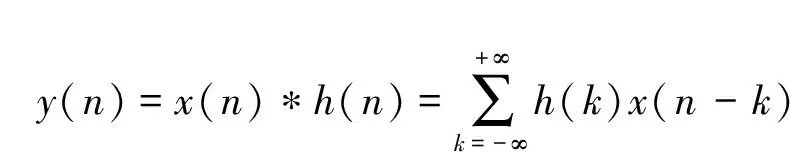
(2)

式中:x(n)为原始信号;y(n)为时间域希尔伯特变换后的信号;h(n)为希尔伯特因子,是一个无穷序列,并且随n的增加而逐渐衰减。h(n)表达式为:

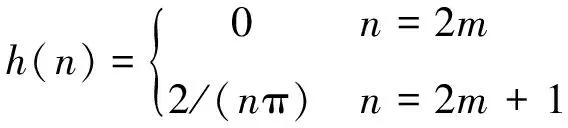
(3)

其中,m为整数。

理想情况下滤波因子无限长,滤波后的结果准确,但在实际应用中,数字滤波所能处理的滤波因子只能是有限长的,所以将滤波因子截断为有限长。滤波因子截断后会出现吉普斯现象,使滤波后的结果发生畸变,对滤波结果产生干扰。

为了解决常规希尔伯特变换对噪声敏感、抗噪能力差的问题,Luo等[6]提出了广义希尔伯特变换,引入了窗函数和阶数,从两个方面对传统的希尔伯特变换进行了扩展。广义希尔伯特变换可以看作是加窗希尔伯特变换,通过使用两端逐渐衰减的窗函数,可以使滤波因子逐渐变为零,从而减小截断效应,达到理想的效果。

加窗处理通过局部增益加权,使得有效边缘信息更加突出,和非边缘信息产生明显差异。选取不同窗函数会有不同的效果[12],窗函数长度因子的选择是控制水平方向多尺度分辨率的关键,大尺度和小尺度因子能分别刻画出不同大小的地质体特征,突显出不同尺度的不连续信息。

本文的仿真模型和实际数据处理选用汉宁窗(即升余弦窗)函数,其表达式为:

(4)

式中:N为自然数,即控制水平方向分辨率的多尺度因子(时窗因子)。N越大,尺度越大,分辨率越低;N越小,尺度越小,分辨率越高。当N=31时,升余弦窗函数如图1所示。

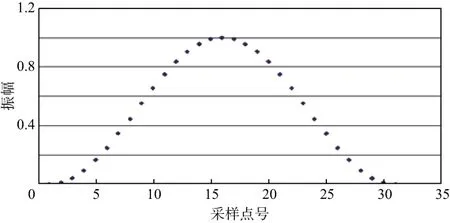
图1 汉宁窗函数

将升余弦窗与希尔伯特因子相乘：

(5)

其中,h′(n)为加窗希尔伯特算子,随着时窗因子的改变,h′(n)也发生改变。加窗希尔伯特变换可表示为：

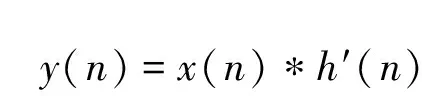
(6)

其中,y(n)为加窗希尔伯特变换后的信号,随着h′(n)的变化而变化,所以也具有多尺度特征。

图2为阶梯形边缘和斜坡形边缘模型的一维模拟信号;图3是利用不同长度窗函数计算的希尔伯特变换结果,可见边缘处的绝对幅值相对极大,位置对应准确,而无边缘信息的部分绝对幅值相对极小。通过比较可以看出,加窗希尔伯特变换准确地提取出了模拟信号的边缘信息,且随着窗长度N的增加,边缘变粗,分辨率降低,反之亦然。因此,窗长度N可用于调节边缘检测结果的分辨率(与不同地质体的尺度大小相对应),检测具有多尺度信息的不连续性特征。

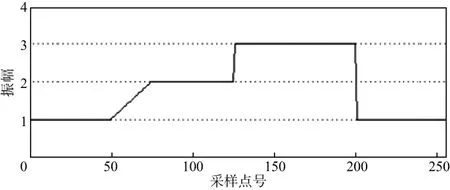
图2 阶梯形边缘和斜坡形边缘模型的一维模拟信号

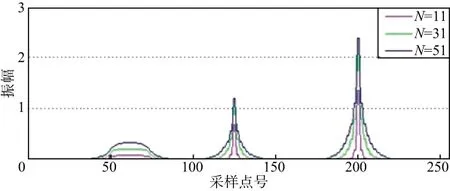
图3 边缘模型一维信号的加窗希尔伯特变换边缘提取

1.2 基于加窗希尔伯特变换的多尺度体边缘检测

由于二维(水平)边缘检测是针对目标层段的单一样点计算的,反映的只是断层或裂缝发育带在这一层位横向上的变化,为水平方向不连续信息的多尺度显示,能够提取的边缘特征是极其有限的。而断层或裂缝发育带等不连续信息的边缘特征在深度方向也是有延伸的,存在深度方向的多尺度特征，深度方向选取的孔径大小不同,突显出的地质体信息各不相同。所以,我们提出基于多尺度加窗希尔伯特变换的体边缘检测方法,同时在水平方向和深度方向上选取不同孔径进行三维多尺度体边缘检测[13],以保证所提取储层内地质异常体信息的完整性。

同时沿水平方向和深度方向采用不同孔径进行多尺度体边缘检测的计算公式为:

(7)

式中:z(n,k,t)表示多尺度体边缘检测结果;i表示深度方向以目标层位为基准向上、下延拓的样点数(正值向下延拓,负值向上延拓);-k和k为深度方向延拓样点数的上、下限(深度方向孔径样点数为2k+1);dt+i·Δt,x(x,y)和dt+i·Δt,y(x,y)分别表示沿x和y方向对地震数据进行处理(t表示目标层位,Δt表示相邻样点之间的采样间隔);h′(n)为(5)式所示的加窗希尔伯特算子。

1.3 多尺度体边缘检测方法实现步骤

基于多尺度加窗希尔伯特变换体边缘检测方法的计算流程如下:

1) 根据给定目标层位,从三维地震数据中提取目标层段的地震数据d(x,y),其中x为工区的总测线数,y为工区单条测线的道数;

2) 对d(x,y)进行保边平滑滤波(edge preserving smoothing,EPS)[14]预处理,以保证断层、裂缝等不连续性信息的地震反射去除噪声以及其它干扰的影响,得到预处理结果dEPS(x,y);

3) 选取不同的计算孔径(水平方向的窗长N及深度方向的样点数i),利用公式(7)对dEPS(x,y)进行多尺度加窗希尔伯特变换体边缘检测计算,得到边缘检测切片集z(n,k,t);

4) 对体边缘检测结果z(n,k,t)进行显示。

2 实际地震资料处理效果分析

以南海某海区三维地震资料为例进行方法测试。该区域目标层段裂缝发育,不连续信息明显,图4是提取的研究工区目标层位沿层切片。

采用本文提出的多尺度加窗体边缘检测方法对目标层位沿层切片进行边缘检测试处理,图5是水平孔径固定为11,深度孔径分别为1，5和11的计算结果。其中深度孔径为1的计算结果(图5a)实际上即为传统的二维(水平)加窗希尔伯特变换检测结果。通过对比可以看出,无论是在分辨率还是信噪比方面,本文提出的三维(体)加窗多尺度边缘检测结果(图5b,图5c)均明显优于二维(水平)加窗边缘检测结果(图5a)。由于考虑了深度方向的异常信息,三维(体)加窗希尔伯特变换结果突出了不同尺度下不连续性信息的完整异常特征,能够更有效地描述裂缝发育带的分布及断层的位置和走向,由此证明了基于多尺度加窗希尔伯特变换体边缘检测方法的有效性。

图4 南海某海区三维地震资料目标层位沿层切片

通过图5也可以看出,采用本文方法选取不同的深度孔径可以得到不同的检测效果。深度孔径较小时(图5b)“背景”较为干净,大的裂缝发育带等不连续性信息比较清晰,分辨率相对较高;随着深度孔径变大(图5c),裂缝、断层的连续性和延展性更加完整,能更好地反映断层和裂缝的走向与分布情况。

选取不同的水平孔径也会得到不同的检测效果。图6是深度孔径固定为11,水平孔径分别为5,31和101得到的三维(体)加窗边缘检测结果。对比可见小水平孔径的优势在于断层和裂缝显示清晰、分辨率高及易于主要异常的定位;而大水平孔径可以突出高信噪比,更好地反映不连续性地质异常的完整特征。

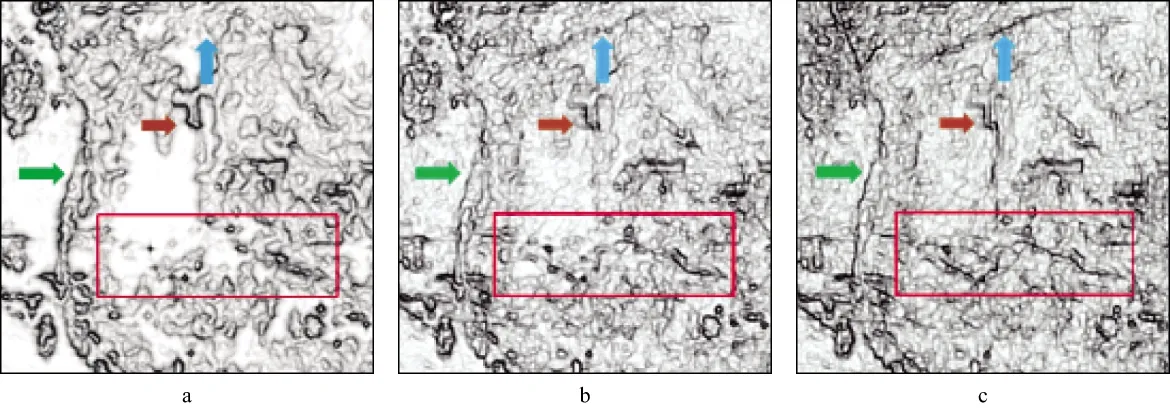
图5 南海某海区三维地震资料采用传统方法与本文方法的边缘检测结果(水平孔径均为11)

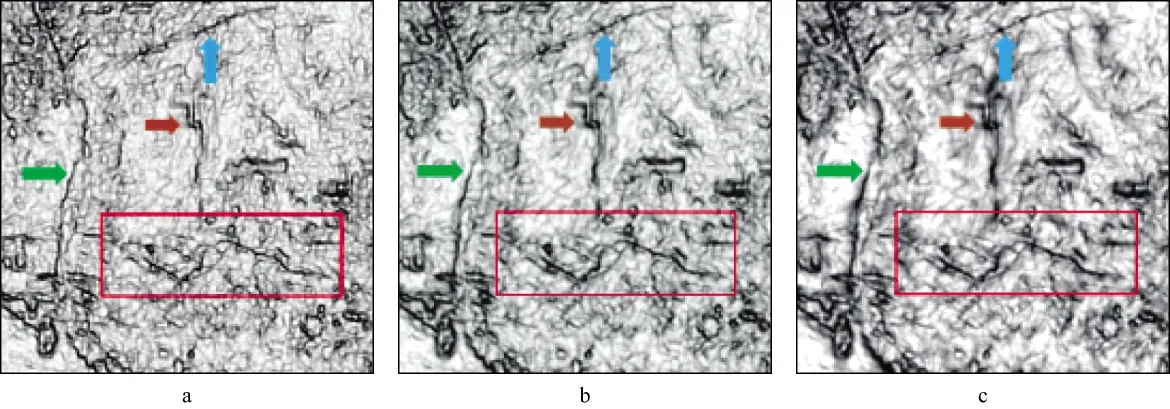
图6 南海某海区三维地震资料采用本文方法的体边缘检测结果(深度孔径均为11)

3 结束语

在二维(水平)加窗希尔伯特变换的基础上,本文提出了基于多尺度加窗希尔伯特变换的体边缘检测方法。通过同时在水平和深度方向上采用不同的孔径提取地质异常体的边缘信息,可以在不同尺度刻画出不连续性三维地质异常体的完整特征,有效地突出裂缝发育带的边缘位置及断层的位置和走向。实际地震资料的试处理结果表明,作为一种新的地震资料边缘检测方法,本文方法具有较为显著的实用价值,可望在裂缝性油气藏的地震储层预测中发挥效用。在水平和深度方向上采用不同孔径能够得到不同的检测效果,所以在实际应用中需要对不同孔径的体边缘检测图像进行对比和综合分析,选取最佳的水平孔径和深度孔径,以提高对地震资料不连续性信息检测的完整性和准确性。

致谢：感谢成都理工大学优秀科研创新团队培育计划(KYTD201410)对本文研究工作的支持。

[1] 李红星,刘财,陶春辉.图像边缘检测方法在地震剖面同相轴自动检测中的应用研究[J].地球物理学进展,2007,22(5):1607-1610 Li H X,Liu C,Tao C H.The study of application of edge measuring technique to the detection of phase axis of the seismic setion[J].Progress in Geophysics,2007,22(5):1607-1610

[2] 罗梦贞.传统的图像边缘检测算法的分析与比较[J].电脑知识与技术,2011,7(16):3907-3909 Luo M Z.The analysis and comparison of traditional image edge detection optimization[J].Computer Knowledge and Technology,2011,7(16):3907-3909

[3] Bahorich M,Farmer S.3D seismic discontinuity for faults and stratigraphic features:the coherence cube[J].The Leading Edge,1995,14(10):1053-1058

[4] 贺振华,黄捍东,胡光岷,等.地下介质横向变化的地震多尺度边缘检测技术[J].物探化探技术,1999,24(4):289-294 He Z H,Huang H D,Hu G M,et al.Lateral identification by seismic multi-scale edge detection[J].Computing Techniques for Geophysical and Geochemical,1999,24(4):289-294

[5] Roberts A.Curvature attributes and their application to 3D interpreted horizons[J].First Break,2001,19(2):85-100

[6] Luo Y,Saleh A,Marhoon M,et al.Generalized Hilbert transform and its applications in geophysics[J].The Leading Edge,2003,22(3):198-202

[7] 党志敏,贺振华,黄德济.GHT在含噪信号边缘检测中的应用效果分析[J].石油工业计算机应用,2008,16(2):19-21 Dang Z M,He Z H,Huang D J.GHT application results analysis in noisy signal edge detection analysis[J].Oil Industry Computer Applications,2008,16(2):19-21

[8] 陈学华,贺振华,文晓涛,等.基于广义S变换的裂缝分频边缘检测方法[J].吉林大学学报(地球科学版),2011,41(5):1605-1609 Chen X H,He Z H,Wen X T,et al.Fracture multi-frequency edge detection based on generalized S transform[J].Jilin University Journal(Earth Sciences),2011,41(5):1605-1609

[9] 张贤达,保铮.非平稳信号分析与处理[M].北京:国防工业出版社,1998:20-25 Zhang X D,Bao Z.Non-stationary signal analysis and processing[M].Beijing:Defense Industry Press,1998:20-25

[10] 陈学华.时频分布与地震信号谱分析研究[D].成都:成都理工大学信息工程学院,2006 Chen X H.Time-frequency distribution and investigation in spectral analysis of seismic signal[D].Chengdu:College of Information Engineering,Chengdu University of Technology,2006

[11] 陈学华,贺振华,黄德济.地震资料的高阶伪希尔伯特变换边缘检测[J].地球物理学进展,2008,23(4):1106-1110 Chen X H,He Z H,Huang D J.Seismic data edge detection pseudo Hilbert based on higher-order transform[J].Progress in Geophysics,2008,23(4):1106-1110

[12] 刘丽娟,王山山.广义S变换窗函数的分析和改进[J].岩性油气藏,2007,19(2):76-79 Liu L J,Wang S S.Analysis and improvement of window function of generalized S-transform[J].Lithologic Reservoirs,2007,19(2):76-79

[13] 伍鹏,陈学华,贺振华,等.基于小波分频的地震资料相干属性对比分析[J].长江大学学报,2011,8(1):39-42 Wu P,Chen X H,He Z H,et al.Comparative analysis of seismic data coherence properties of wavelet-based crossover[J].Yangtze University Journal,2011,8(1):39-42

[14] Luo Y,Maher M.Edge-preserving smoothing and applications[J].The Leading Edge,2002,21(2):136-141

[15] 赵岩,贺振华,黄德济.基于保边去噪的高精度相干分析应用研究[J].长江大学学报,2009,6(4):169-171 Zhao Y,He Z H,Huang D J.Based on analysis of the coherent application of precision edge-preserving denoising[J].Yangtze University Journal,2009,6(4):169-171

(编辑：戴春秋)

Seismic data 3D edge detection based on multi-scale windowed Hilbert transform

Li Bin1,2,Chen Xuehua1,2,He Zhenhua1,2,Xu Di2,Li Yijia2,Pei Xiaogang2,Tang Xiangrong2

(1.StateKeyLaboratoryofOil&GasReservoirGeologyandExploitation,ChengduUniversityofTechnology,Chengdu610059,China; 2.KeyLaboratoryofEarthExplorationandInformationTechnology,MinistryofEducation,ChengduUniversityofTechnology,Chengdu610059,China)

The identification of discontinuity abnormal information in seismic data,such as the seismic responses from faults or fracture zone,is crucial to fractured oil-gas reservoir prediction.Therefore,we proposed a new 3D edge detection method based on multi-scale windowed Hilbert transform.It is based on 2D (horizontal) windowed Hilbert transform，considering the characteristics of 3D multi-scale for discontinuous geological anomalies.The edge information of 3D geological anomalies is calculated by simultaneously adjusting the aperture in the horizontal and depth direction,thus overcame the obvious inadequacy of edge information extracting only in the spatial direction for 2D (horizontal) windowed Hilbert transform.Trial processing results of the actual seismic data for 3D edge detection show that the method can completely describe the characteristics of multi-scale discontinuous geological anomalies,effectively reveal the location and direction of fractures developed zone and faults with more significant practical value.

3D edge detection,generalized Hilbert transform,multi-scale features,horizontal space aperture,depth aperture

2014-06-17;改回日期：2014-10-19。

李斌(1990—)，男，硕士在读，主要从事地震信号分析与储层结构地震检测方面的研究。

国家自然科学基金项目(41374134，41174114)、四川省杰出青年科学基金(2013JQ0011)和国家科技重大专项项目(2011ZX05023-005-010)联合资助。

P631

A

1000-1441(2015)03-0345-05

10.3969/j.issn.1000-1441.2015.03.014