最小二乘逆时偏移成像方法的实现与应用研究

2015-06-27郭书娟马方正段心标

石油物探 2015年3期

郭书娟,马方正,段心标,王丽

(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2.同济大学海洋与地球科学学院，上海200092;3.中国石油化工股份有限公司江苏油田分公司物探技术研究院，江苏南京210046)

郭书娟1，2,马方正1,段心标1,王丽3

复杂岩性油气藏勘探开发需要高保真的地震成像资料。与常规偏移方法相比，最小二乘逆时偏移(LSRTM)成像基于反演理论，可为岩性储层估计提供更加保真的高分辨率反射系数成像剖面，成为当前成像方法的研究热点和发展趋势。通过对误差泛函建立、逆时反偏移数据重构算法、Hessian逆预条件梯度计算及基于高斯-牛顿法的反演迭代更新方法等关键技术研究，实现了迭代最小二乘逆时偏移成像。为了使该偏移成像方法能够应用于实际资料，研究了针对性的数据预处理技术和最小平方匹配滤波模拟数据校正处理技术，探索建立了面向实际资料的最小二乘逆时偏移实现流程。某探区实际二维地震资料的最小二乘逆时偏移成像结果表明，相比传统的逆时偏移成像技术，最小二乘逆时偏移在成像分辨率和保幅性方面具有一定的优势。

最小二乘逆时偏移;逆时反偏移;Hessian逆预条件梯度;高斯-牛顿法;预处理;匹配滤波

随着油气勘探的深入，对岩性成像的需求越来越迫切，对成像方法的保真度需求不断提高。现有的常规积分偏移算法(如Kirchhoff偏移)或波动方程偏移(如单程波或RTM)用正向传播算子的共轭(或转置)作为偏移算子作用于地震数据中，将波场反传外推至成像点，用一定的成像条件来定位反射点的位置。这些方法更侧重于几何结构成像，无法满足岩性储层描述对保幅成像的要求。基于反演理论的最小二乘偏移方法把成像问题当作一个反问题来处理，通过比较由偏移剖面所产生的合成数据与实际采集数据之间的相关性来判定成像结果是否准确。通过多次自动修正成像结果来提升相关性，以寻求更接近于真实的地下反射系数，从而更好地进行岩性储层成像和储层参数反演。该方法是实现地震成像理论由常规地下岩石的几何结构描述向保幅成像的推进和发展，具有更高的成像精度，也是实现高精度储层参数反演的关键。

最小二乘偏移反演思想最初由LeBras等提出[1]，Lambaré等[2]进行了补充和完善;Tamas等[3]提出了基于Kirchhoff的最小二乘偏移方法，用于偏移不规则的反射地震数据(如地震道缺失、采样不规则)，消除由于数据不规则带来的偏移假象;Duquet等[4]提出最小二乘偏移在处理起伏地表照明和由不规则粗采样的地震波场引起的成像误差时比Kirchhoff偏移具有更大优势;Kuehl等[5-6]将波动方程延拓算子应用到最小二乘偏移,提出了最小二乘裂步偏移算法，并于2002年采用最小二乘双平方根(DSR)偏移算法提取AVP/AVA道集，模型数据测试结果说明该偏移算法提取的AVA道集与真实的AVA道集有较高的匹配度，对不完整数据比常规偏移有更好的适应性;Plessix等[7]、Guy等[8]、Ren等[9]和Wang等[10]详细分析了最小二乘偏移技术的本质及其在复杂介质成像中的优越性;Dai等[11-12]和Tang[13]将逆时偏移算子引入到最小二乘偏移中处理多震源成像问题，采用相位编码技术提高成像效率，以提高最小二乘偏移技术的实用能力。最小二乘偏移技术相较于常用的偏移成像算法，如Kirchhoff类偏移、单程波类偏移以及双程波偏移，具有更好的保幅性和更高的精度，并对不规则数据具有更强的适应性，正成为国际上的研究热点和偏移成像方法技术的发展趋势。

近年来国内一些学者也开展了相关研究。杨其强等[14]研究了最小二乘傅里叶有限差分偏移方法，并给出了简单模型试算的成像结果;沈雄君等[15]研究了裂步法最小二乘偏移，介绍了用于地震波有效频带内的最小二乘偏移算法和实施步骤;黄建平等[16-18]实现了最小二乘Kirchhoff偏移算法和最小二乘逆时偏移(LSRTM)方法，通过模型试算说明了该方法能够提高成像保幅性，基于最小二乘逆时偏移压制低频成像噪声的优势，说明了该方法在近地表高精度成像中的潜力。刘玉金等[19]实现了局部倾角约束的最小二乘偏移方法，讨论了最小二乘偏移对缺道不规则数据成像的优势;王华忠等*王华忠，胡江涛.面向岩性油气藏的最小二乘叠前深度偏移成像.WPI年度研究报告，2013分析和推导了最小二乘叠前深度偏移的原理，并基于模型测试说明了该方法可以提高成像分辨率和保幅性，展示了该方法在岩性油气储层精细描述中的应用潜力。

以上文献大多是通过最小二乘偏移在理论模型中的测试结果来说明方法技术的优势和特点，少有分析最小二乘偏移在处理实际问题时的难点及应对策略，目前在国内尚未见到实际资料的应用实例。本文主要从误差泛函建立、逆时反偏移数据重构算法、Hessian逆预条件梯度计算及基于高斯牛顿法的反演迭代更新方法等几方面进行研究，实现迭代最小二乘逆时偏移成像。针对最小二乘偏移方法实际应用时所关注的问题，研究最小平方匹配滤波模拟数据校正处理技术，探索建立最小二乘偏移用于实际资料时的技术流程，并用模型数据和实际资料试算结果说明本文方法及其技术流程的有效性和适用性。

1 最小二乘逆时偏移方法原理

在介质密度为常数的假设前提下，频率-空间域的波动方程为：

(1)

式中：x表示地下介质空间坐标；rs表示炮点坐标；u表示总波场；s(x)为介质的慢度；ω表示频率；δ(x-rs)是脉冲函数，震源位置在rs；f(ω)表示震源。

在研究区域X内，介质的扰动关系可以表述为：

(2)

式中：s0(x)为介质的背景慢度；Δs(x)为介质慢度的扰动，即散射源或散射势。

总波场分解为背景波场(或入射波场)和散射波场，即：

(3)

式中：u0表示背景波场；us表示散射波场。背景波场u0满足：

(4)

将(2)式、(3)式和(4)式代入(1)式，基于Born近似忽略高阶项，可得：

(5)

引入背景介质中Green函数，该Green函数满足方程：

(6)

可得背景入射波场和Born近似下散射波场分别为：

(7)

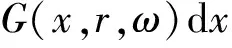
(8)

(8)式描述了一个忽略了二阶以上散射波，仅描述波传播过程中的一阶散射波的传播现象。Born近似的物理实质是：在背景场u0中没有散射场;在扰动场中，只存在一次散射场。尽管用这种方式描述波传播与严格的预测所有波现象的最小二乘逆时偏移不符，但由于实际背景速度不准确，目前对LSRTM的讨论基于(8)式，称之为线性化LSRTM[20]。

波场正向传播算子L也是反偏移算子，其表达式为：

(9)

(8)式定义的积分方程写成矩阵形式为：

Lm=us

(10)

为估计模型参数扰动m，采用最小二乘方法求解方程(10)，建立如下二次型误差泛函：

(11)

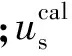
(12)

式中：(LTL)-1代表Hessian逆矩阵。

解如(12)式所示法方程进行最小二乘叠前深度偏移时有两个问题：①法方程本身是误差泛函，关于模型参数扰动的导数等于0;②全Hessian的逆无法计算[20]。因此迭代类的最小二乘偏移成像是目前常用的实现方式，每轮迭代计算都要完成残差计算，求取残差反传播梯度及用Hessian逆矩阵预条件梯度，通过迭代来逐步减小数据拟合误差。

最小二乘偏移的目标是寻求目标泛函能量最小化的最优成像值，是一最优化问题。研究中采用高斯-牛顿法进行反演成像迭代更新，其表达式为：

(13)

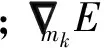
(14)

(15)

由于求解全Hessian矩阵的逆计算量巨大，而且是主对角占优矩阵，因此在最小二乘偏移中为了提高计算效率常采用Hessian矩阵的对角元素近似代替Hessian矩阵。对角Hessian矩阵可以表示为[20]：

(16)

最小二乘偏移是基于反演理论的成像方法，算法核心是根据反偏移模拟数据与观测数据的匹配程度来判定成像的准确性，并根据残差对成像结果进行修正。用于理论模型时，速度模型、数据正演模拟算法、震源子波都是已知的，提高了数据匹配程度。但是对于实际资料，由于地下介质、波场传播过程及采集条件的复杂性，无法真正实现完全模拟地震数据，其原因为：①数据模拟算法因素——地下介质和波场传播复杂，波动方程无法模拟出全部的波场，尤其是声波假设情况下;②采集因素——野外采集条件复杂多样，会产生很多干扰和噪声，这些噪声无法通过反偏移算法模拟出来，会影响数据残差的准确求取，影响方法的收敛性和稳定性，需要从观测数据中对其进行消除;③子波因素——实际震源子波是空变的，每炮都可能各不相同，难以准确估计，影响数据模拟精度。此外，速度、密度等参数估计误差也会增加实际数据准确模拟的难度。总之，对于实际资料来说，除了成像不精确引起的反偏移模拟数据与实际观测数据之间的误差之外，还有很多其它因素的影响，需要尽量消除，为基于数据残差进行成像更新提供相对纯净的环境。

探索并建立了如图1所示的面向实际资料的最小二乘偏移成像技术流程。此流程针对最小二乘偏移技术用于实际资料时所关注的问题，根据最小二乘偏移技术的数据预处理原则，采用最小平方匹配滤波方法进行反偏移模拟数据校正。

在预处理阶段，反偏移算法不能模拟的波场及噪声都要从观测数据中消除。最小二乘偏移在数据噪声较强时，会将噪声放大，得不到较好的成像结果。在声波近似情况下，面波和直达波等波场也要消除，要根据实际资料的特点选取针对性的去噪流程，原则是要尽量采用保真度高的去噪方法，避免损害有效信号。

为消除由于子波及其它因素带来的观测数据与反偏移模拟数据之间的振幅差异，设法对反偏移模拟数据进行振幅校正，使振幅与观测数据处于同一量级，再求取数据残差。采用(17)式给出的误差能量泛函：

(17)

式中：m(ω,x)代表匹配因子。

采用最小平方匹配滤波方法来求取匹配因子，使得反偏移模拟数据与观测数据振幅能量数量级一致，通过莱文森(Levinson)快速递推算法求解(18)式以求得匹配因子[20]。

(18)

式中：K是匹配因子的长度;αrr(ω,x)是反偏移模拟数据的自相关;αor(ω,x)是反偏移模拟数据与观测数据的互相关。其中，

(19)

(20)

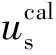
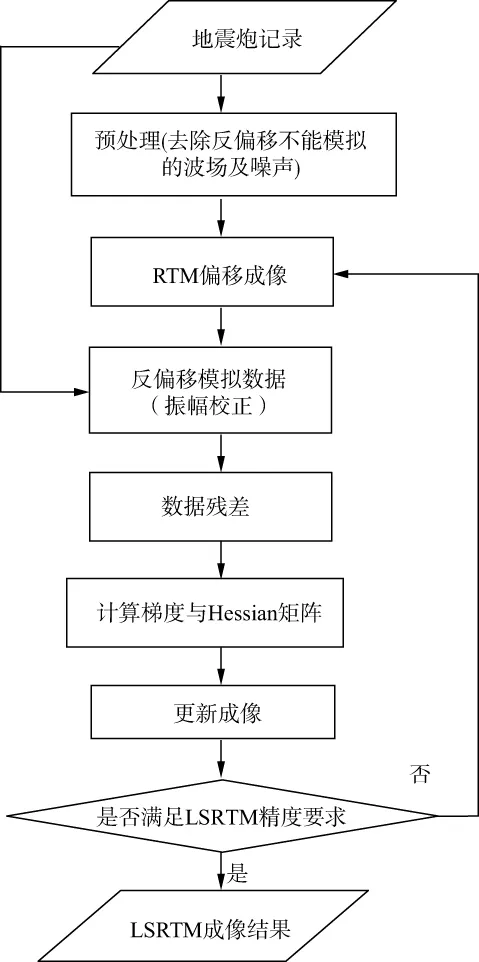
图1 面向实际资料的最小二乘逆时偏移流程

2 数据测试

2.1 模型测试

采用图2所示的经典盐丘模型数据对本文方法进行测试，该盐丘模型中有几组较为明显的高陡断层。作为模型数据，预处理环节只需要去除直达波。由于数据正演所用震源已知，故反偏移模拟数据振幅校正环节也可忽略。

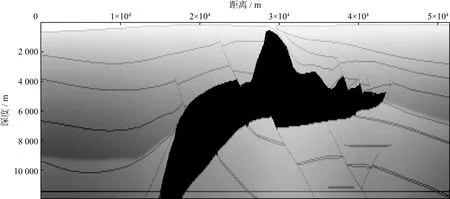
图2 盐丘速度模型

图3a和图3b分别是逆时偏移和最小二乘逆时偏移迭代30次的成像结果。对比图3a和图3b可见，最小二乘偏移成像结果提高了剖面振幅均衡性，盐丘翼部中深层部分成像更加清晰，中深层小尺度构造展布更为清晰。

图4a和图4b分别是逆时偏移成像结果和最小二乘逆时偏移结果与真实反射系数单道振幅的对比。可以看出，最小二乘逆时偏移与真实反射系数振幅更加接近，具有更高的保幅性。图5是迭代最小二乘逆时偏移数据残差收敛曲线，说明此方法在模型测试过程中数据残差稳步收敛，残差逐渐变小，成像精度越来越高。

图3 逆时偏移(a)和最小二乘逆时偏移(b)成像结果

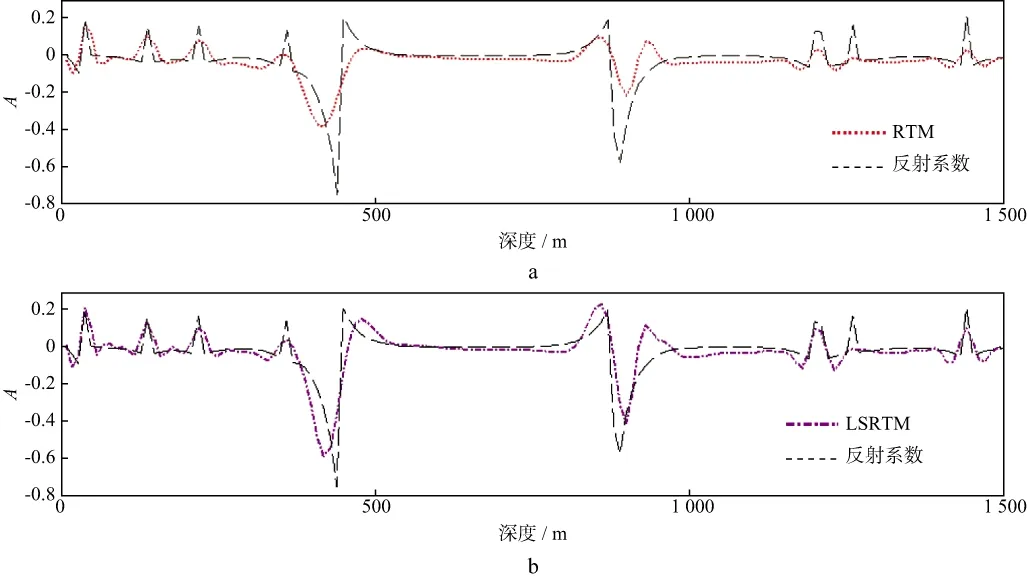
图4 模型数据逆时偏移(a)和最小二乘逆时偏移(b)与真实反射系数单道振幅的对比

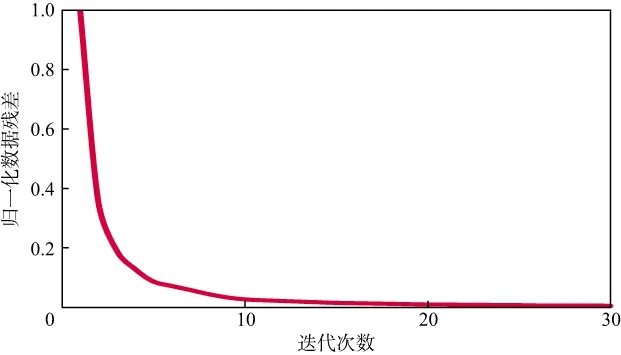
图5 模型数据最小二乘逆时偏移数据残差收敛曲线

2.2 二维实际资料测试

采用某实际陆上地震资料对本文方法进行验证。该套二维数据共117炮，每炮240道，道间距40m。地震资料中面波、折射波、不规则强干扰发育。根据本文提出的技术流程，需对资料进行预处理。在剔除异常振幅和直达波之后，选用保真度高的去噪方法，如噪声自动识别与衰减、炮集自动统计道编辑、时空域相干噪声衰减等技术，压制原始资料中存在的上述干扰波，确保各种强能量干扰得到很好的压制，同时不损失有效波。

图6a和图6b分别给出了观测数据和基于初始逆时偏移的反偏移模拟数据。可见反偏移模拟数据与观测数据相位基本一致，说明速度场精度较高，满足最小二乘逆时偏移成像的要求。然后，按照本文所述流程对反偏移模拟数据进行迭代更新。在每次迭代过程中，基于最小平方匹配滤波方法对反偏移模拟数据进行了校正，使其与观测数据振幅能量数量级一致后再求取数据残差。

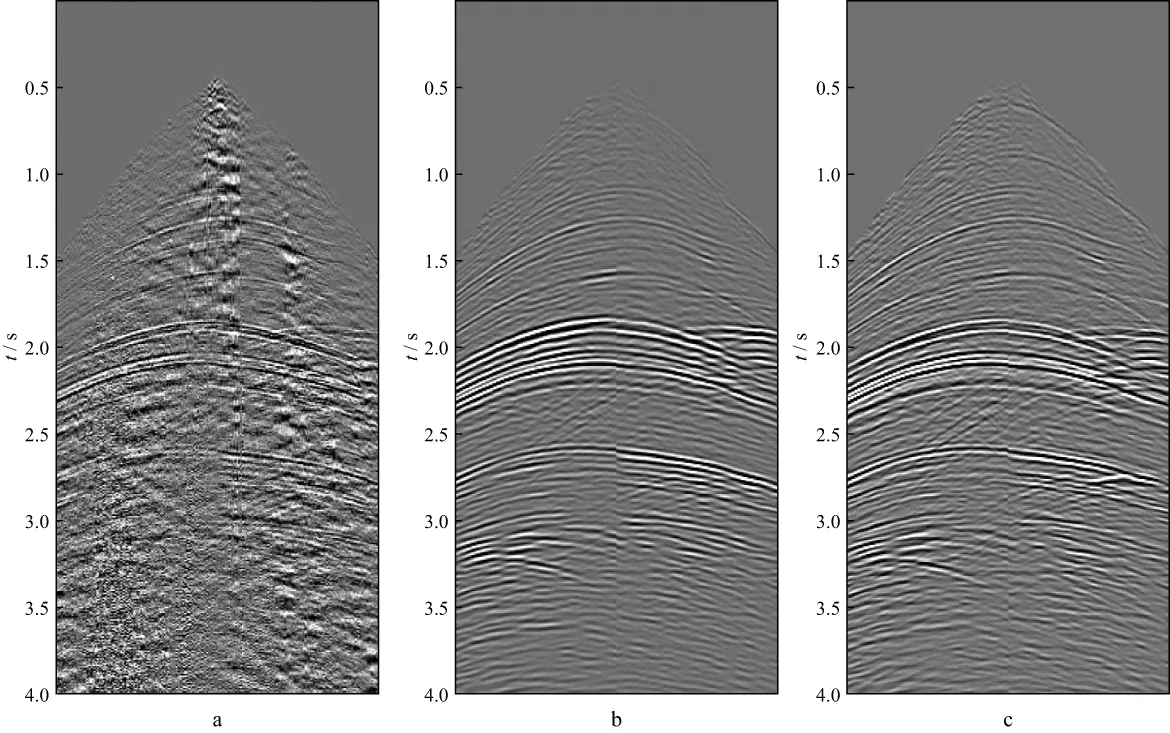
图6 观测数据(a)、基于初始逆时偏移的反偏移模拟数据(b)及基于最小二乘逆时偏移的反偏移模拟数据(c)

图6c是基于最小二乘逆时偏移结果第8次迭代的反偏移数据。对比图6b和图6c可见，基于最小二乘逆时偏移结果重构的数据频率更高，与实际观测数据更加吻合。

图7为随着迭代次数增加某单炮数据残差收敛曲线。可以看到，随着迭代次数增加，数据残差稳定收敛，说明了本文方法对研究区资料的适用性。随着逐次迭代，数据残差逐渐减小，说明在成像过程中逐步加入了更丰富的有效信息，实现了有效信息利用最大化，从而有利于一些弱有效信号的利用，提高了成像分辨率和保幅性。

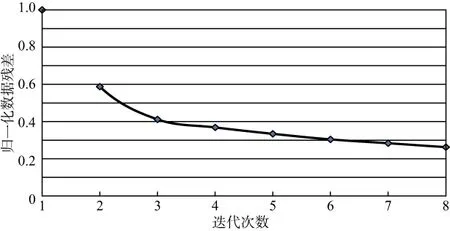
图7 实际资料最小二乘偏移不同迭代次数数据残差曲线

图8a和图8b分别是二维实际资料逆时偏移与最小二乘逆时偏移成像结果。对比图8a和图8b 可见，最小二乘偏移成像结果浅层成像更加清晰，分辨率更高，中深层部分如左下方椭圆内小断块成像更加干脆、清晰。图9是逆时偏移和最小二乘逆时偏移成像结果频谱分析。可以看出，最小二乘逆时偏移成像结果提高了主频，拓宽了有效频带，提高了分辨率，同时也展示了最小二乘逆时偏移在小尺度构造如小断块等刻画方面的应用潜力。

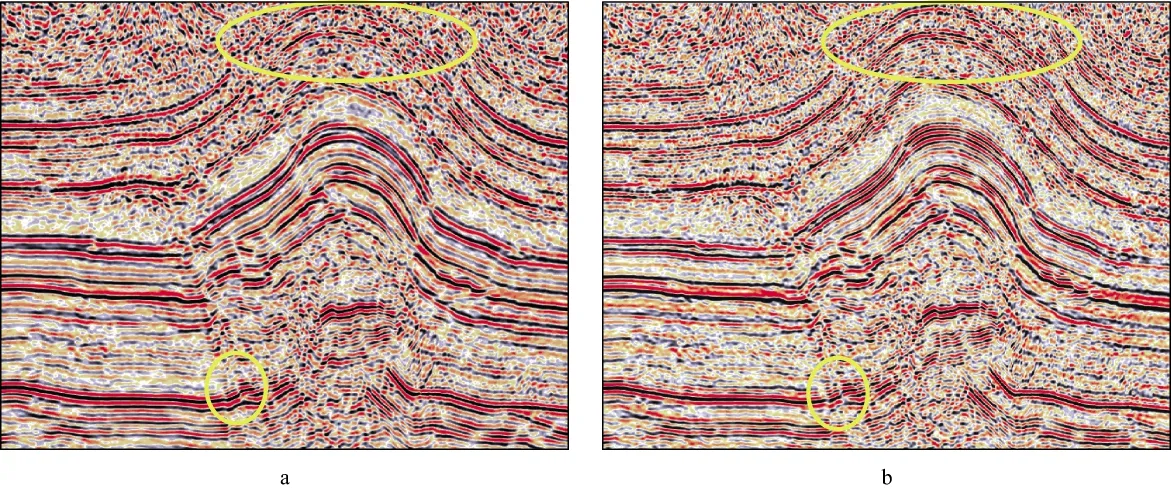
图8 二维实际资料逆时偏移成像结果(a)和最小二乘逆时偏移成像结果(b)

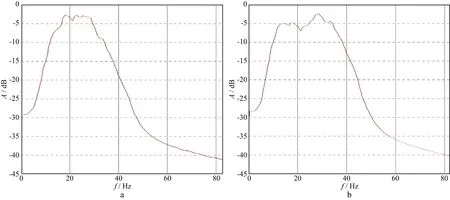
图9 二维实际资料成像结果频谱分析

3 结论与讨论

研究了最小二乘逆时偏移成像方法的实现过程，分析了最小二乘逆时偏移方法应用于实际地震资料时的预处理原则，阐述了最小平方匹配滤波方法进行反偏移模拟数据校正的原理，探索建立了实用化的最小二乘逆时偏移成像技术流程。模型测试和实际资料试处理结果说明了本文方法的有效性和适应性。与常规逆时偏移方法相比，本文方法提高了成像结果的分辨率与保幅性，更有利于后续岩性储层成像。

建立面向实际资料的最小二乘逆时偏移技术流程要遵循的原则是:尽量消除成像不精确之外的因素对数据残差的影响，为基于数据残差进行成像更新提供更加纯净的环境。此外，最小二乘逆时偏移技术用于实际资料时还需要注意以下几方面。

1) 震源子波。最小二乘逆时偏移寻求反偏移模拟记录和实际记录的最佳匹配，震源子波的波形和能量决定了模拟地震记录的振幅甚至相位，对地震子波的研究是最小二乘逆时偏移反演成像能否得到好结果的一个重要因素。

2) 速度模型。在实际资料处理时，地震速度误差是不可避免的。基于背景速度进行的第一次偏移结果不能有大的误差，才有必要进行最小二乘逆时偏移来提高成像精度。实际地下反射系数是反射角度的函数，但目前常用的反偏移都是基于叠加成像剖面进行反偏移数据模拟，这就会导致中、远偏移距模拟数据存在比较严重的由于速度误差引起的数据时差问题。研发基于道集的反偏移算法，是完善最小二乘逆时偏移方法所需要攻关的方向之一。

3) 计算效率。最小二乘逆时偏移的计算量约为常规偏移的2.5N(N为迭代次数)倍，因此，当遇到大规模的尤其是三维地震数据时，计算量就是很大难题。用基于编码的最小二乘逆时偏移或者引入GPU加速都可以大幅提高最小二乘逆时偏移的计算效率，从而满足实用需求。这也是最小二乘逆时偏移成像技术应用研究中的另一个重要课题。

[1] LeBras R,Clayton R W.An iterative inversion of back-scattered acoustic waves[J].Geophysics,1988,53(4):501-508

[2] Lambaré G,Virieux J,Mandariaga R,et al.Iterative asymptotic inversion in the acoustic approximation[J].Geophysics,1992,57(9):1138-1154

[3] Tamas N,Wu C J,Gerard T.Least-squares migration of incomplete reflection data[J].Geophysics,1999,64(1):208-221

[4] Duquet B,Marfurt J K,Dell inger J A.Kirchhoff modeling,inversion for reflectivity,and subsurface illumination[J].Geophysics,2000,65(4):1195-1209

[5] Kuehl H，Sacchi M D.Split-step WKBJ least-squares migration/inversion of incomplete data[J].Expanded Abstracts of 5thSEGJ International Symposium Imaging Technology,2001,200-204

[6] Kuehl H，Sacchi M D.Least-squares wave-equation migration for AVP/AVA inversion[J].Geophysics,2003,68(1):262-273

[7] Plessix R E，Mulder W A.Frequency-domain finite-difference amplitude-preserving migration[J].Geophysical Journal International,2004,157:975-987

[8] Guy C,Ren’e-Edouard P.An optimal true-amplitude least-squares prestack depth-migration operator[J].Geophysics,1999,64(2):508-515

[9] Ren H，Wu R S，Wang H.Wave equation least square imaging using the local angular Hessian for amplitude correction[J].Geophysical Prospecting,2011,59(4):651-661

[10] Wang J,Kuehl H，Sacchi M D.Least-squares wave-equation AVP imaging of 3D common azimuth data[J].Expanded Abstracts of 73rdAnnual Internat SEG Mtg,2003,1039-1042

[11] Dai W,Schuster G T.Multi-source wave equation least-squares migration with a deblurring filter[J].Expanded Abstracts of 72ndEAGE Conference & Exhibition Incorporating SPE Europec,2010,276-281

[12] Dai W,Wang X，Schuster G T.Least-squares migration of multisource data with a deblurringfilter[J].Geophysics,2011,76(5):R135-R146

[13] Tang Y.Target-oriented wave-equation least-squares migration/inversion with phase-encoded Hessian[J].Geophysics,2009,74(6):WCA95-WCA107

[14] 杨其强，张叔伦.最小二乘傅立叶有限差分偏移[J].地球物理学进展，2008,23(2)：433-437 Yang Q Q,Zhang S L.Least-squares Fourier finite-difference migration[J].Progress in Geophysics,2008,23(2)：433-437

[15] 沈雄君，刘能超.裂步法最小二乘偏移[J].地球物理学进展，2012,27(2)：761-770 Shen X J,Liu N C.Split-step least-squares migration[J].Progress in Geophysics,2012,27(2):761-770

[16] 黄建平，李振春,孔雪，等.碳酸盐岩裂缝型储层最小二乘偏移成像方法研究[J].地球物理学报，2013,56(5)：1716-1723 Huang J P,Li Z C,Kong X,et al.A study of least-squares migration imaging method for fractured-type carbonate reservoir[J].Chinese Journal Geophysics,2013,56(5)：1716-1723

[17] 黄建平，李振春,刘玉金，等.复杂介质最小二乘叠前深度偏移成像方法[J].地球物理学进展，2013,28(6):2977-2983 Huang J P,Li Z C,Liu Y J,et al.The least-squares pre-stack depth migration on complex media[J].Progress in Geophysics(in Chinese),2013,28(6):2977-2983

[18] 黄建平，曹晓莉,李振春，等.最小二乘逆时偏移在近地表高精度成像中的应用[J].石油地球物理勘探，2014,49(1):107-112 Huang J P,Cao X L,Li Z C,et al.Applications of least square reverse time migration in the near surface high precision imaging[J].Oil Geophysical Prospecting,2014,49(1):107-112

[19] 刘玉金，李振春,吴丹，等.局部倾角约束最小二乘偏移方法研究[J].地球物理学报，2013,56(3):1003-1011 Liu Y J,Li Z C,Wu D,et al.The research on local slope constrained least-squares migration[J].Chinese Journal Geophysics(in Chinese),2013,56(3):1003-1011

[20] 牟永光，陈小宏，李国发，等.地震数据处理方法[M].北京：石油大学出版社,2004：1-278 Mou Y G,Chen X H,Li G F,et al.Seismic data process methods[M].Beijing:Petroleum Industry Press,2004:1-278

(编辑：陈杰)

Research of least-squares reverse-time migration imaging method and its application

Guo Shujuan1,2,Ma Fangzheng1,Duan Xinbiao1,Wang Li3

(1.SinopecGeophysicalResearchInstitute,Nanjing211103,China;2.TongjiUniversity,Shanghai200092,China;3.GeophysicalTechnologicalInstituteofJiangsuOilfield,SINOPEC,Nanjing210046,China)

High fidelity imaging method is required by complex lithology reservoir exploration and development.Compared with the conventional migration method,least-squares migration imaging based on inversion theory could provide high resolution imaging with more fidelity for lithologic reservoir estimation,which is becoming a research focus and trend of migration imaging method.We establish the functional error,reserve-time de-migration data reconstruction algorithm,Hessian inverse preconditioned gradient calculation and inversion iteration updating based on Gauss-Newton method,to realize the least-squares reverse-time migration imaging.In order to make it available to the field data,we study targeted data preprocessing and least-squares matching filter simulation data correction technology and build least square reserved-time migration workflow oriented to field data.The imaging results of least-squares reserve-time migration to an actual seismic data shows its advantages in imaging resolution and amplitude preservation,compared with conventional reverse-time migration technique.

least-squares reverse-time migration,reserve-time de-migration (RTDM),Hessian reverse preconditioned gradient,Gauss-Newton method,data preprocessing,matching filter

2014-03-13;改回日期：2014-07-27。

郭书娟(1984—)，女，博士，现主要从事地震成像方法研究工作。

国家科技重大专项(2011ZX05014-001-002)专题资助。

P631

1000-1441(2015)03-0301-08

10.3969/j.issn.1000-1441.2015.03.008