分层介质目标电磁散射计算的快速射线追踪方法

张 磊王 超董纯柱，2侯兆国殷红成，2

分层介质目标电磁散射计算的快速射线追踪方法

张 磊1王 超1董纯柱1，2侯兆国1殷红成1，2

（1.电磁散射重点实验室，北京100854；2.中国传媒大学信息工程学院，北京100024）

针对利用射线追踪方法计算分层介质目标散射时由于海量射线导致的资源和效率瓶颈问题，提出了改进的蒙特卡洛法和自适应射线细分法，实现对超电大分层介质目标高频电磁散射的快速计算.改进的蒙特卡洛法基于射线在介质分界面上反射和折射的能量分布，将射线分裂等效为按照特定概率发生反射或折射，射线追踪过程中射线数保持不变，而自适应射线细分法通过选择稀疏的初始射线，并根据目标结构和材质的变化自动细分加密，在保证计算精度的同时最大程度降低射线数.仿真试验与参考结果对比验证了本文方法的精确和高效，并分析了两种方法的优缺点，给出了适用范围以及在实际工程应用中的建议.

分层介质结构；射线追踪法；电磁散射；蒙特卡洛法；自适应射线细分法

引 言

作为一种典型结构形式，分层介质广泛存在于各类人造目标、建筑物、地物环境，如天线罩、建筑物、地表土壤等.研究满足工程应用要求的分层介质目标电磁散射特性计算方法，对天线罩设计、穿墙探测、埋地目标探测等研究具有重要应用价值［1－7］.

电磁波照射介质目标时会穿入介质，在分界面上同时存在反射和折射现象.计算介质目标电磁特性不但要考虑目标几何外形，还要考虑材料电磁参数和空间分布.对于分层介质目标，目标由若干厚度不均匀的介质层组合而成，每一层介质电磁参数均匀（或近似等效均匀），但各层厚度及形状较为复杂，其散射过程较金属目标、均匀介质体目标等更为复杂.传统的解析方法，如半空间法、传输线法、模式匹配法等［8－9］只能用于无限大均匀分层介质的电磁特性计算，无法满足复杂外形和材料分布的情形.目前，针对具有复杂外形和材料分布的分层介质目标，主要采用两类计算方法：一类是精确数值方法，如时域有限差分法（Finite Difference Time Domain，FDTD）、矩量法（Method of Moments，MoM）等［1014］；另一类是基于几何光学和波前光学的高频渐近方法［1，15］.前者基于电磁场积分或微分方程，能精确计算电磁波与介质的相互作用，但受计算资源的限制，目前难以满足电大复杂分层介质目标电磁散射特性计算的需求.后者从散射机理出发，以光学射线弹跳追踪［16－17］为基础，利用等效射线在目标内的反射和折射追踪计算电磁波的能量传递，快速获取目标的电磁散射特性，相对于精确数值方法，高频方法计算效率高，资源需求少.

然而，对于超电大复杂分层介质目标，传统的射线追踪算法依然面临资源和效率的制约，主要体现在：初始射线数巨大，且射线数随追踪深度（射线碰撞次数）的增加呈指数增长.针对上述资源和效率瓶颈问题，本文在射线分裂方法的基础上，提出了改进的蒙特卡洛法和自适应射线细分法，实现对超电大分层介质目标高频电磁散射的快速计算.蒙特卡洛法中射线与介质分界面每一次碰撞只发生反射或折射，其反射／折射概率均取0.5［18］，而改进的蒙特卡洛法对电磁波在介质分界面上随机反射或折射的概率进行修正，使其概率与介质分界面上反射／折射的能量相关.自适应射线细分法基于射线管自适应分裂技术［19－20］，采用稀疏的初始射线照射目标，根据相邻射线反射和折射的方向差异自动细分加密射线，即在几何结构和材料参数变化剧烈的区域采用更多的射线，而在较为平直和均匀的区域采用较少的射线，在保证计算精度的前提下能够显著降低射线数.基于介质平板和建筑物类目标的数值算例，与文献和测量数据的比较验证了本文方法的精确和高效.通过分析两种方法的优缺点及各自适用范围，对该方法在实际工程中的应用提出了有益的建议.

1 射线分裂方法的原理

根据几何射线理论，当入射射线照射介质分界面时，由于两侧电磁参数（折射率）的差异，电磁波会在表面发生反射和折射现象，反射和折射射线分别携带一部分能量继续传播.分裂的射线在下一个碰撞到的分界面上继续分裂直至离开目标或能量衰减到足够小后停止.

利用射线分裂方法计算电磁波能量传递时主要考虑两个因素：传播方向和能量衰减.前者通过空间几何运算确定射线与介质分界面的交点和反射／折射方向，称为射线路经追踪；后者计算电磁波在传播过程中场强和相位的变化，称为射线场追踪［17，21］.当射线离开介质目标外表面时，直接利用物理光学（Physical Optics，PO）法计算目标的散射场.

1.1射线路径追踪

图1给出了射线在分层介质目标上的传递过程.一根入射射线与介质分界面发生碰撞后会产生射线分裂，形成反射射线与折射射线，分裂后的射线继续传播，碰撞到下一个分界面后继续分裂.显然，随着碰撞次数增加，射线数呈指数增长，而射线能量呈指数衰减.

射线路径追踪首先要确定射线与介质分界面的交点，即碰撞点位置，然后计算射线与介质分界面碰撞后反射与折射方向.对于复杂分层介质目标，通常采用平面元网格模拟介质分界面，根据平面元空间几何关系，结合射线方程求解碰撞点位置.射线在碰撞点分裂后，反射／折射射线的方向需要根据材料电磁参数利用反射定律或折射定律进行计算.对均匀无耗介质，折射方向可直接利用Snell定律计算，而对于均匀有耗介质，则需要对公式进行修正，具体公式和推导过程参考文献［21］.

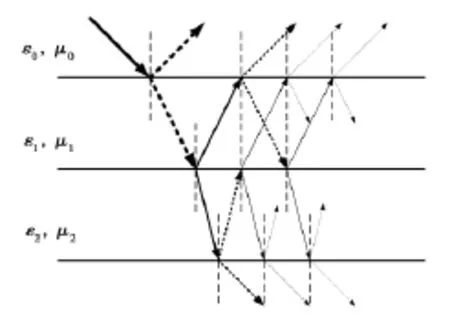
图1 射线分裂示意图

1.2射线场追踪

在射线路径追踪的基础上还需要进一步计算射线的能量传递，即射线场追踪.反射／折射场的幅度分别为入射场幅度乘以反射／折射系数的模，再乘以空间衰减因子；相位由反射／折射系数的相角和波程相位延迟两部分组成.

定义如下单位矢量：

碰撞点处入射、反射和折射场的电场强度矢量分别表示为：

式（3）～（5）中：场分量Ei／／和Ei⊥分别为入射电场的平行极化分量和垂直极化分量；R／／和T／／分别为平行极化的反射和折射系数；R⊥和T⊥分别为垂直极化的反射和折射系数.反射／折射系数计算公式参考文献［22］.

值得注意的是，折射到有耗介质中的电磁波，其等幅面与等相位面是不一致的，是一种非均匀平面波［22］，在计算折射波传播衰减时需注意折射波幅度的衰减方向.

图2所示为射线在介质分界面S上发生碰撞时发生反射与折射的过程示意图.图中，θi、θr和θt分别为入射角、反射角和折射角，O为目标坐标系原点，P为碰撞点位置为S的外法向矢量，其他参量定义同上.

图2 射线追踪的反射和折射示意图

通过推导可知，相对于入射场的相位，反射场和折射场的附加波程相位分别表示为：

式中：φi为入射场相位；φr为反射波程相位；φt为折射波程相位；ki、kt分别为入射场、折射场所在介质层的波数.

1.3散射场计算

当射线离开介质目标外表面时会产生散射，可利用PO法计算射线的散射场，参考文献［23］，介质目标远区散射场的PO公式可表示为：

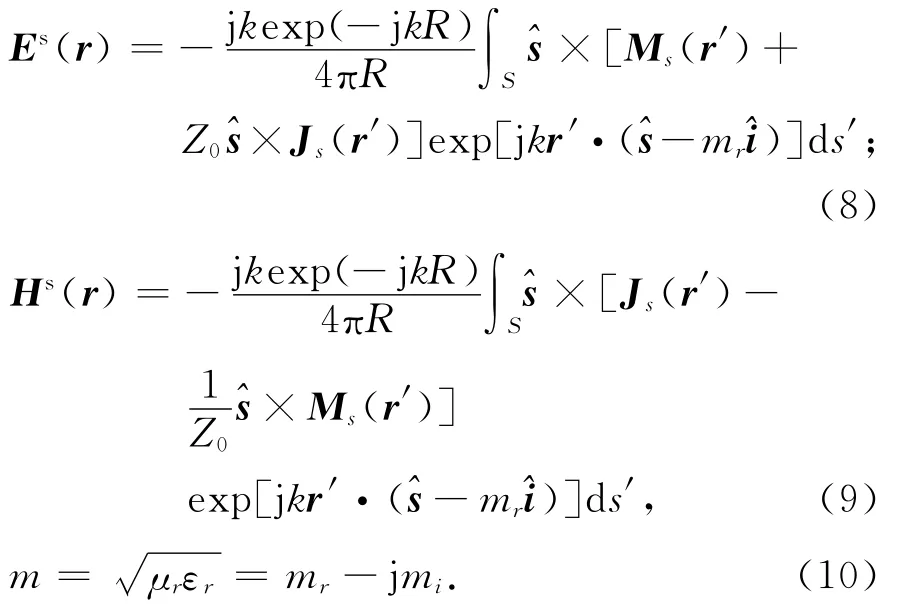
对于介质外表面的直接反射射线，其等效流为：

式中，Ei（r′），Hi（r′）和Er（r′），Hr（r′）分别为介质表面的入射场和反射场.

对于重新折射出介质目标的射线，其等效流为：

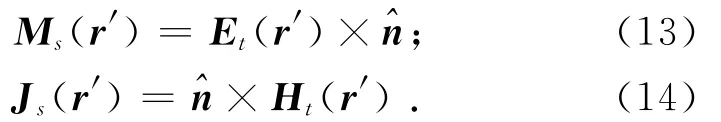
式中，Et（r′），Ht（r′）为折射场.

2 分层介质目标快速射线追踪方法

传统的射线追踪方法要求射线管的尺寸小于十分之一个介质波长.当目标电尺寸较大时，射线数目非常大（通常能达到数百万量级），且随着追踪深度（碰撞次数）呈指数增加，造成内存开销和计算时间急剧上升.为克服射线分裂方法在计算分层介质目标的不足，考虑从控制射线分裂过程以及降低初始射线数两条途径进行优化，在保证计算精度前提下，尽可能减少射线数.

2.1改进的蒙特卡洛法

射线分裂导致射线数指数增加，为降低射线数，应尽可能考虑避免分裂计算.图3所示为蒙特卡洛射线追踪算法原理.入射射线与介质分界面碰撞后，随机发生反射或折射［18］，射线数不随追踪深度变化.

图3 蒙特卡洛射线追踪示意图

文献［18］中射线反射或折射的概率均为0.5，由于相对介质阻抗的不同，分界面上反射和折射的能量分配不均匀，射线反射／折射的概率与能量分配一致，能更加准确模拟电磁波的传递规律.本文提出基于能量传递分布的修正概率计算模型，即反射概率为反射场能量除以入射场能量，折射概率为折射场能量除以入射场能量.根据电磁场的能量守恒定律，可以推导出以下概率计算公式：

式中：Z1、Z2分别为入射场和折射场所在空间波阻抗；Pr和Pt分别为反射和折射概率.将概率与能量分配相结合，能够有效考虑能量传递的主要贡献分量，提高计算精度.

蒙特卡洛射线追踪方法的优势是射线追踪过程中，射线数保持不变，内存开销随追踪深度线性增加，计算效率高.然而，由于每一次计算都会损失一部分射线信息，射线追踪过程不完备，会缺失散射能量较弱的细节信息.

2.2自适应射线细分法

对于超电大介质目标，目标结构和材料的空间变化相对于波长而言非常缓慢，在射线追踪过程中，大多数射线都相互平行，即满足平面波条件.对于介质结构的曲率或法向变化较大的地方（突变区域、局部细节），射线不满足平行条件，可通过细分加密射线，提高计算精度.具体根据以下三个条件判断是否细分：

1）判断射线追踪深度是否达到设定的最大追踪深度，若达到，则结束射线追踪和细分；

2）判断射线的横截面积是否小于某一阈值，若是，则不再进行细分，阈值一般取0.004 33λ2，其中λ为介质波长；

3）判断相邻射线与介质分界面的碰撞点处的法向夹角是否大于某一阈值（根据精度的不同，精度越高，阈值越小，一般取5°～10°），若是，则在两射线之间细分加密射线，如图4所示，实线表示初始射线，虚线为细分加密的射线.其中的特殊情况是，相邻射线中有射线未与介质分界面发生碰撞，也需要进行细分加密.

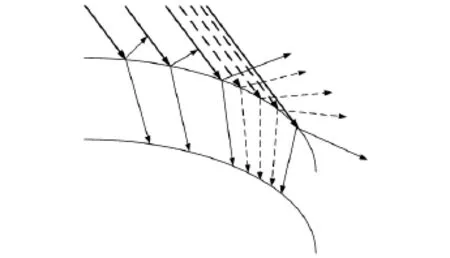
图4 自适应射线细分示意图

一般说来，初始射线的密度可以由目标结构尺寸和曲率变化确定（一般可选择数十个波长），相对于与传统射线法，初始射线密度可降低3～4个量级.结合射线预追踪、模型预处理等技术［19－20］可以进一步在选择初始射线时进行优化.

对于超电大平直或曲率缓变的分层介质目标，该方法计算效率能够提高1～2个量级，并具有相当高的计算精度，但对于复杂目标结构和形状，加速效率会降低.

3 仿真示例与分析

为验证本文方法的正确性和有效性，以介质平板、墙体与立方体金属块组合结构和建筑物三个模型为例，利用本文方法开展仿真计算，并与实测结果和文献结果进行比较.

3.1介质平板

如图5所示，电磁参数为εr＝4.1－j0.016，μr＝1.0的介质平板垂直放置于YOZ面内，平板边长为1 000mm×500mm，厚度为10mm.频率f＝4 GHz的电磁波沿水平方向入射，图6给出了介质平板HH极化单站雷达散射截面（Radar Cross Section，RCS）的计算结果与实测数据对比.

图5 介质平板示意图

图6 介质平板单站RCS计算与实测结果对比

由图6对比可知，改进的蒙特卡洛法和自适应射线细分法计算的介质平板单站RCS与实测数据在0°～50°范围内吻合较好，在50°～90°范围内与实测数据存在一定偏差，但量级基本保持一致.

为验证自适应射线细分法的计算稳定性，分别采用不同稀疏程度的初始射线进行计算，图7给出了初始射线数分别为40 602和2 578的结果对比.

图7 自适应射线细分法不同初始射线数计算结果对比

由图7可知，对不同的初始射线数（两者相差16倍），自适应射线细分法计算的结果吻合较好，仅在70°～90°近掠入射范围存在偏差，表明了自适应射线细分法具有良好的稳定性.

3.2墙体和立方体金属块组合结构

为验证改进的蒙特卡洛法对计算精度的提高，构造图8所示的墙体与立方体金属块组合结构，其中墙体尺寸为5m×2.2m×0.2m，电磁参数为εr＝3.8－j0.24，μr＝1，三个立方体金属块边长均为0.1m.中心频率2.5GHz，带宽2GHz的电磁波沿水平方向入射，垂直极化.图9给出了文献［18］方法与改进的蒙特卡洛法的一维距离像对比.

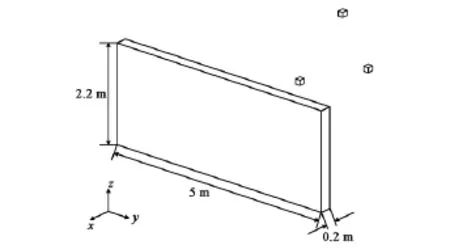
图8 墙体和小金属块组合结构

对比图9可知，两幅图中前三个峰值的位置与幅度基本相同，且峰值位置与目标结构散射中心的位置相对应.第一个峰值产生于墙体前面的反射，第二个峰值产生于墙体后面的反射，第三个峰值同样产生于墙体后面的反射（电磁波传播两个来回）.三个峰值等间距且大于墙体的厚度，因为电磁波在介质中的传播速度比空气中慢.

比较两幅图可以看出，图9（a）较图（b）少一个峰值，该峰值对应第一个立方体金属块，即文献中蒙特卡洛法没有检测到该散射中心，其它两个立方体金属块对应的峰值吻合较好.分析可知，蒙特卡洛法的基本特征是随机反射或折射，计算结果具有一定的随机性，当样本数增大时结果区域稳定.大量仿真实验表明，采用文献中蒙特卡洛法计算时由于射线的平均分布，透射射线丢失概率较高，结果不稳定，大多为两个峰值或一个峰值；而采用改进的蒙特卡洛法，由于射线概率和能量相关，透射射线丢失概率降低，三个立方体金属块对应的散射中心均会出现，计算稳定性好.

图9 两种方法得到的一维距离像结果比较

综上分析，在相同射线数下，改进的蒙特卡洛法计算精度和稳定性更高.当然，通过增加射线数，可以提高文献方法计算精度，但会降低计算效率.

3.3建筑物模型

选择内部有人型介质体的建筑物目标为例进行仿真计算［1］，验证本文方法在计算复杂模型时的精度和效率.建筑物模型如图10（a）所示，尺寸为5m ×3.5m×2.2m，墙壁厚度为0.2m.建筑物墙体由砖块砌成，电磁参数εr＝3.8－j0.24，μr＝1.建筑物底部和顶部为混凝土地板和天花板，厚度均为0.15 m，电磁参数εr＝6.8－j0.9，μr＝1.人型均匀介质体目标（人体3D模型）位于建筑物中心［24］，电磁参数为εr＝50－j12，μr＝1，其尺寸近似取成年男子平均尺寸.电磁波沿水平方向入射，垂直极化.图10给出了建筑物在中心频率2.5GHz，带宽2GHz，合成孔径角40°时的仿真成像结果与文献［1］结果，其中孔径角中心角度对应方位角0°.

对比本文与文献Xpatch（基于射线追踪方法）和FDTD仿真结果可知，本文计算结果与文献结果的强散射中心的分布形状、位置、强度等特征均吻合较好，主要差异分析情况如下：文献［1］算例说明中建筑物尺寸为5m×3.5m×2.2m，根据其算例结果中模型轮廓图，其实际计算尺寸为5m×3.65m ×2.2m，本文计算结果位置与理论计算一致；墙壁散射强度偏差较小，人型介质体偏差主要来源于模型差异.

图中自左向右分别存在左端三条直线、中心一个散射点和右端两条直线.分析可知，左端三条直线为左墙壁的反射，分别对应外表面反射、内表面一次反射（电磁波在墙壁中传播一个双程）和内表面二次反射（电磁波在墙壁中传播两个双程）；中心散射点为人的散射；右侧两条线是右侧墙壁内表面以及外表面的反射.壁后面存在明显的遮挡阴影，这与实际情况也是相符合的.此外，通过模型轮廓与图像对比可以发现，直线和散射点的位置相对于几何模型在观测方向上滞后，这是由于电磁波在介质中传播速度比空气中慢而造成的空间延迟.介质墙壁的空间延迟（d为墙壁厚度），通过理论分析，本文计算结果散射中心位置是准确的.

对比图10本文计算的三幅图像的差异.图（b）中传统射线分裂法成像结果与文献中结果吻合最好，图像最为清晰；图（c）中改进的蒙特卡洛法计算的成像结果中人的强度太弱；图（d）中自适应射线细分法成像结果与文献中结果吻合较好，但出现了较弱的杂瓣.分析可知，传统的射线分裂法因为没有采取任何的近似和加速措施，计算过程最为严格，精度最高；改进的蒙特卡洛法由于自身算法存在信息不全，射线随机反射或折射导致弱信号的缺失；自适应射线细分法得到的图像结果相对改进的蒙特卡洛法较为理想，但在边界上由于自适应细分时可能会引入噪声（细分过程的截断误差），这种噪声通常非常微弱.

最后，对三种方法计算效率和内存需求进行定量比较，表1给出了传统射线分裂法、改进的蒙特卡洛法和自适应射线细分法的计算时间和内存消耗（射线追踪深度均为9层）.显然，改进的蒙特卡洛法计算效率最高，相对传统射线分裂法计算效率提高约94倍，内存需求是传统方法的1／13；自适应射线细分法相对传统射线分裂效率提高约11倍，内存需求约为传统方法的1／12.

图10 建筑物模型以及成像结果

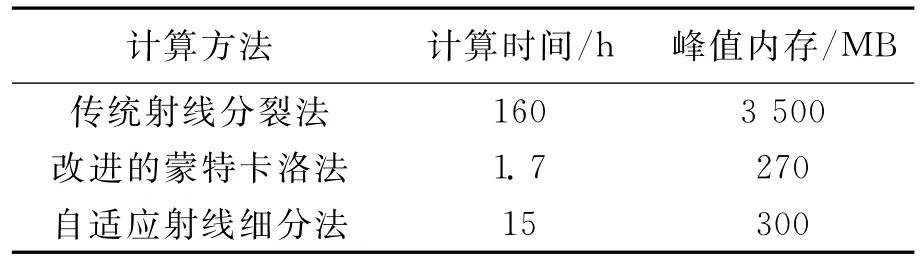
表1 三种射线追踪方法计算时间和内存需求

值得一提的是，本算例均采用均匀分布的初始射线，未结合几何结构进行优选.通过增加蒙特卡洛法的初始射线数，可能进一步提高其计算精度，而优化初始射线分布，在保证计算精度的条件下可以进一步提高自适应射线细分法的效率.在实际应用中，改进的蒙特卡洛方法使用最为方便、高效，可用于快速预估计算，而自适应射线细分适合于精细计算，两种算法在计算精度和计算效率之间均可以较为方便地控制.

4 结 论

本文提出了改进的蒙特卡洛法和自适应射线细分法两种快速计算分层介质目标电磁散射的方法，突破了传统射线分裂方法海量射线数对计算机内存资源需求和计算效率的瓶颈.仿真实验与参考结果对比，验证了本文方法是准确和高效的，在实际使用中可结合两种方法的优势.

通过实际仿真实验的内存开销和时间统计可知，峰值内存与射线数以及追踪深度密切相关，通过分批计算可以在不影响计算精度和效率的前提下降低内存需求，计算时间主要受路径追踪和场追踪计算影响，其过程中还存在较多冗余计算，且所有射线的计算均是相互独立的，非常适合于开展并行加速.进一步挖掘算法的优化和加速技术是本文的下一步研究工作.

［1］ LE C，DOGARU T，NGUYEN L，et al.Ultrawideband（UWB）radar imaging of building interior：measurements and predictions［J］.IEEE Trans Geosci Remote Sens，2009，47（5）：1409－1420.

［2］ CHANG P C，BURKHOLDER R J，VOLAKIS J L，et al.High－frequency EM characterization of throughwall building imaging［J］.IEEE Trans Geosci Remote Sens，2009，47（5）：1375－1387.

［3］ 任晶晶，柴守刚，陈卫东.基于混合计算方法的脉冲超宽带穿墙散射建模［J］.电波科学学报，2012，27（5）：859－866.

REN Jingjing，CHAI Shougang，CHEN Weidong.Hybrid technique combining time domain ray－tracing and FDTD method for IR－UWB signal through－thewall scattering modeling［J］.Chinese Journal of Radio Science，2012，27（5）：859－866.（in Chinese）

［4］ WANG Juan，GUO Gaofeng，ZHENG Hu，et al.Characteristic analysis of nose radome by aperture－integration and surface－integration method［C］／／IEEE MMWCST.April 19－20，Chengdu，2012.

［5］ SIPUS Z，LANNE M，JOSEFSSON L.Moment method analysis of circular cylindrical array of waveguide elements covered with a multilayer［J］.IEE Proc－Microw Antennas Propag，2006，153（1）：29－37.

［6］ FREZZA F，PAJEWSKI L，PONTI C，et al.Scattering by perfectly conducting circular cylinders buried in a dielectric slab through the cylindrical wave approach［J］.IEEE Trans Antennas Propag，2009，57（4）：1208－1217.

［7］ GONZALEZ－HUICI M A，USCHKERAT U，HOERDT A.Numerical simulation of electromagneticwave propagation for land mine detection using GPR［C］／／IEEE Geosci Remote Sens Symposium，2007：4957－4960.

［8］ BUSSEY H E，RICHMOND J H.Scattering by a lossy dielectric circular cylindrical multilayer numerical value［J］.IEEE Trans on Antennas and Propagation，1976，23（5）：723－725.

［9］ CHOW W C.Waves and Fields in Inhomogeneous Media［M］.New York：Nostrand Reinhold，1990.

［10］ MICHALSKI K A，ZHENG D.Electromagnetic scattering and radiation by surfaces of arbitrary shape in layered media，part I：theory［J］.IEEE Transaction on Antennas and Propagation，1990（3）：335－344.

［11］ MICHALSKI K A，MOSIG J R.Multilayered media Green’s functions in integral equation formulations［J］.IEEE Trans Antennas Propagat，1997，45（3）：508－519.

［12］ DEMAREST K，PLUMB R，HUANG Z.FDTD modeling of scatterers in stratified media［J］.IEEE Trans Antennas Propagat，43（10），1995：1164－1168.

［13］ 丁大志，刘金权，胡云琴，等.基于多层快速多极子算法分析平面多层结构［J］.电波科学学报，2009，24（3）：422－426.

DING Dazhi，LIU Jinquan，HU Yunqin，et al.Multilayered plane structure using multilevel fast multipole algorithm［J］.Chinese Journal of Radio Science，2009，24（3）：422－426.（in Chinese）

［14］ 王文博，徐金平，夏 冰.复杂多层介质电磁分析的几何建模及剖分技术［J］.电波科学学报，2008，23（5）：950－954.

WANG Wenbo，XU Jinping，XIA Bing.A method for modeling and meshing of multi－layered dielectric structure for analysis of EM problem［J］.Chinese Journal of Radio Science，2008，23（5）：950－954.（in Chinese）

［15］ WANG Gu，YUAN Lei，WANG Taosheng，et al.RCS calculation of complex targets shielded with plasma based on visual GRECO method［C］／／IEEE Microwave Antenna Propaga，EMC Tech Wireless Communications，2009：950－953.

［16］ LING H，CHOU R C，LEE S W.Shooting and bouncing rays：calculating the RCS of an arbitrarily shaped cavity［J］.IEEE Trans Antenna Propagat，1989，37（2）：194－205.

［17］ DIDASCALOU D，SCHAFER T M，WEINMANN F，et al.Ray－density normalization for ray－optical wave propagation modeling in arbitrarily shaped tunnels［J］.IEEE Trans Antennas Propagat，2000，48（9）：1316－1325.

［18］ WEINMANN F.PO／PTD ray tracing for arbitrary metallic and dielectric objects［C］／／European Conference on Antennas ＆Propagation，2006：6－10.

［19］ 殷红成，朱国庆，董纯柱，等.基于自适应射线管分裂的多次反射计算方法［J］.系统工程与电子技术，2013，35（4）：700－706.

YIN Hongcheng，ZHU Guoqing，DONG Chunzhu，et al.Efficient multi－reflection computational method based on adaptive ray tube splitting［J］.Systems Engineering and Electronics，2013，35（4）：700－706.（in Chinese）

［20］ 董纯柱，殷红成，王 超.基于射线管分裂方法的SAR场景快速消隐技术［J］.雷达学报，2012，1（4）：436－440.

DONG Chunzhu，YIN Hongcheng，WANG Chao.A fast hidden surface removal approach for complex SAR scene based on adaptive ray－tube splitting method［J］.Journal of Radars，2012，1（4）：436－440.（in Chinese）

［21］ YANG P，LIOU K N.Effective refractive index for determining ray propagation in an absorbing dielectric particle［J］.J Quant Spectrosc Radiat Transfer，2009，110：300－306.

［22］ 杨儒贵.高等电磁理论［M］.北京：高等教育出版社，2008：41－50.

［23］ 黄培康.雷达目标特性［M］.北京：电子工业出版社，2005.

［24］ DOGARU T，NGUYEN L，LE C.Computer Models of the Human Body Signature for Sensing Through the Wall Radar Applications［R］.Adelphi：MD，Tech Rep ARL－TR－4290，2007.

作者简介

张 磊（1989－），男，安徽人，博士研究生，主要研究方向为目标与环境电磁散射计算方法及计算机加速技术.

王 超（1979－），男，陕西人，高级工程师，主要研究方向为雷达目标特性建模与特征分析.

董纯柱（1981－），男，河南人，高级工程师，主要研究方向为雷达目标特性建模与特征提取.

侯兆国（1983－），男，甘肃人，高级工程师，主要研究方向为雷达目标特性建模与模型评估.

殷红成（1967－），男，江西人，研究员，博士生导师，主要研究方向为雷达目标特性建模与应用.

Fast ray－tracing method for electromagnetic scattering computation of multi－layered dielectric structure

ZHANG Lei1WANG Chao1DONG Chunzhu1，2HOU Zhaoguo1YIN Hongcheng1，2
（1.Science and Technology on Electromagnetic Scattering Laboratory，Beijing100854，China；2.Information Engineering School，Communication University of China，Beijing100024，China）

Both the improved Monte Carlo method and the adaptive ray sub－division method are proposed to solve the bottle－neck problem of computation resource and efficiency resulting from the great number of rays for the ray－tracing method to calculate the electromagnetic（EM）scattering of multi－layered dielectric structure.The improved Monte Carlo method regards ray splitting as reflection or refraction separately based on special probability calculated by the energy distribution of the reflected and refracted rays，and the ray number keeps the same.The adaptive ray subdivision method reduces the number of rays farthest by choosing sparse initial rays，and ensures the calculation accuracy by adaptively adding rays based on the variety of structure and material.Simulation experiments and reference results show that the proposed two methods are accurate and efficient.Finally，the paper analyses the merits and demerits，and points outthe scope of application and suggestions in practical aspect.

multi－layered dielectric structure；ray－tracing method；electromagnetic scattering；Monte Carlo method；adaptive ray subdivision method

TN011

A

1005－0388（2015）02－0208－09

张 磊，王 超，董纯柱，等.分层介质目标电磁散射计算的快速射线追踪方法［J］.电波科学学报，2015，30（2）：208－216.

10.13443／j.cjors.2014051602

ZHANG Lei，WANG Chao，DONG Chunzhu，et al.Fast ray－tracing method for electromagnetic scattering computation of multi－layered dielectric structure［J］.Chinese Journal of Radio Science，2015，30（2）：208－216.（in Chinese）.doi：10.13443／j.cjors.2014051602

2014－05－16

973项目（2010CB731905）

联系人：张磊E－mail：zhangleigcss＠126.com