可逆卡诺制冷机和热泵的输出率密度分析与优化

杨光明，朱朝峰，刘云海

（海军驻武汉四三八厂军事代表室，武汉 430061）

可逆卡诺制冷机和热泵的输出率密度分析与优化

杨光明，朱朝峰，刘云海

（海军驻武汉四三八厂军事代表室，武汉 430061）

以逆卡诺循环的输出率密度（对循环最大比容平均的循环输出率），即卡诺制冷机的制冷率密度和卡诺热泵的供热率密度作为热力性能目标, 分别对内可逆卡诺制冷机和热泵进行分析与优化，导出了最佳换热器面积分配的关系式，计算分析了热源温比对输出率密度与性能系数关系的影响。所得结果不同于以制冷率和供热率为目标的优化结果，对装置设计具有一定理论上的指导意义。

内可逆卡诺制冷机 内可逆卡诺热泵 制冷率密度 供热率密度

0 引言

自NoviKov、Chambadal、Curzon和Ahlborn等人分别导出了著名的CA效率[1-3]后，有限时间热力学的研究取得了大量成果[4-7]。在对制冷机和热泵循环的研究中，严子俊[8-9]和Goth[10]首先研究了卡诺制冷机及热泵的基本优化关系。陈林根等[11]导出了卡诺制冷机的有限时间火 用 经济性能界限、优化关系和优化准则，并建立了制冷机的生态学优化目标[12]。吴治、孙丰瑞、陈林根等[13-15]则研究了卡诺热泵的比供热率、生态学、经济性。陈林根等[16-17]和朱小芹等[18-19]研究了传热规律对不可逆卡诺制冷机[16,18]和热泵[17,19]性能的影响。1996年起，一些学者以对最大比容平均的功率输出—功率密度为优化目标，研究了热机循环的性能优化问题，兼顾了发动机的尺寸和效率[20-23]。Yavuz和Erbay最早用制冷率密度（即制冷率与循环最大比容之比）分别分析研究了Ericsson循环和Stirling循环[24-25]，并得到了有意义的结果。进一步，周圣兵等[26]以制冷率密度为目标对内可逆空气制冷机进行了分析与优化。本文将以逆卡诺循环的输出率密度，即卡诺制冷机的制冷率密度和卡诺热泵的供热率密度作为热力性能目标, 分别对内可逆卡诺制冷机和热泵进行分析与优化，并与以输出率为目标的研究结果进

行比较，所得结果兼顾了装置的尺寸因素，具有一定理论上的指导意义。

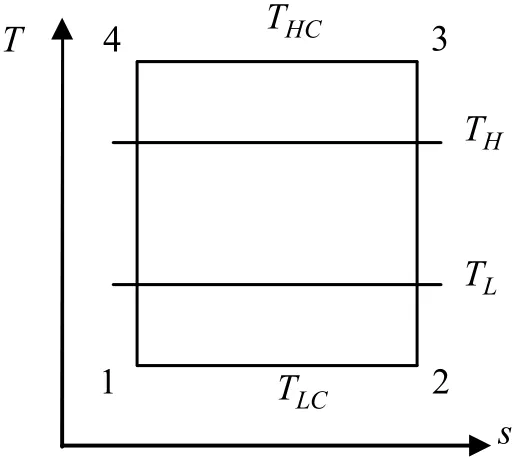
图1 内可逆卡诺制冷机、热泵循环模型

1 循环描述

考虑如图1所示的内可逆卡诺制冷机和热泵循环模型, 假定该模型为定常态流，内可逆卡诺循环，两恒温热源温度分别为TH、TL，高、低温侧工质的温度分别为THC、TLC；过程1-2为从TL热源等温吸热过程，过程3-4为向TH热源等温放热过程，2-3和4-1分别为绝热压缩和绝热膨胀过程。

2 制冷机的制冷率、制冷率密度分析

3 热泵的供热率、供热率密度分析

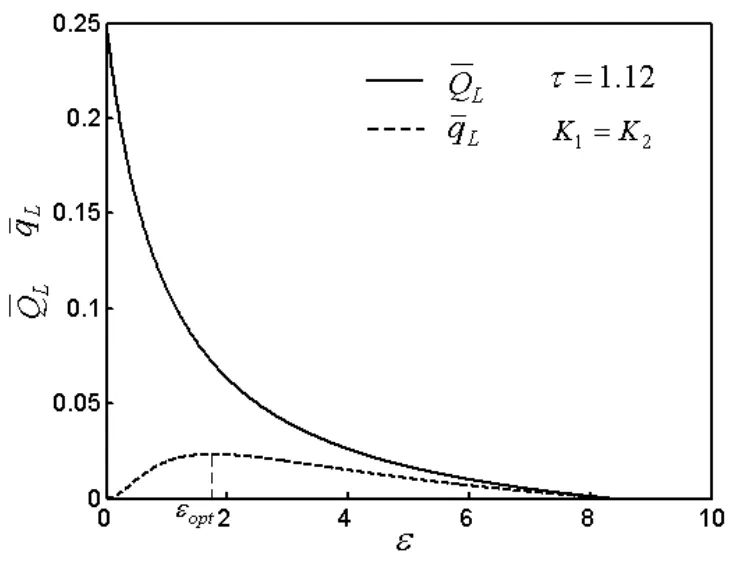
图2 制冷率、制冷率密度与制冷系数的关系曲线

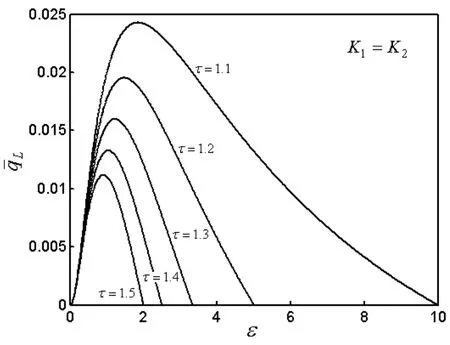
图3 热源温比对制冷率密度性能的影响

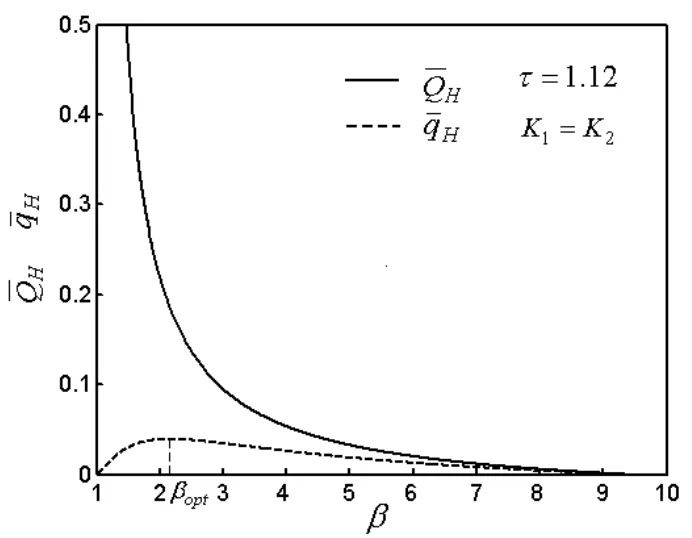
图4 供热率、供热率密度与供热系数的关系曲线

图1中，2点为循环比容最大点，则供热率密度的解析式为

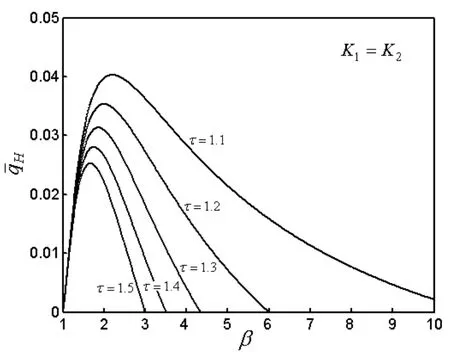
图5 热源温比对供热率密度性能的影响

4 小结

本文以输出率密度为优化目标，研究内可逆卡诺制冷机和热泵性能，着重讨论了制冷机和热泵的制冷率密度和供热率密度与性能系数之间的关系，导出了换热器面积分配的关系式，得到了不同于以传统制冷率和供热率为优化目标的新结果，具有一定理论上的指导意义。不可逆卡诺制冷机和热泵的性能优化问题尚待进一步研究探讨。

[1] Novikov I I. The efficiency of atomic power stations (A review) [J]. Atommaya Energiya 3, 1957(11): 409.

[2] Chambdal P. Les Centrales Nucleases[M]. Paris: Armand Colin, 1957(11): 41-58.

[3] Curzon F L, Ahlborn B. Efficiency of a carnot engine at maximum power output [J]. Am. J. Phys, 1975, 43(1): 22-24.

[4] Bejan A. Entropy generation minimization. The new thermodynamics of finite-size device and finite-time processes [J]. J. Appl. Phys, 1996, 79(3): 1191-1218.

[5] Berry R S, Kazakov V A, Sieniutycz S, Szwast Z, Tsirlin A M. Thermodynamic Optimization of Finite Time Processes [M]. Wiley, Chichester, 1999.

[6] Chen L, Sun F. Advances in finite time thermodynamics: Analysis and Optimization [M]. New York: Nova Science Publishers, 2004, p240.

[7] 陈林根. 不可逆过程和循环的有限时间热力学分析[M]. 北京: 高等教育出版社, 2005, p280.

[8] 严子浚. 卡诺制冷机的最佳制冷系数与制冷率关系[J]. 物理, 1984, 13(12): 768-770.

[9] 严子浚. 内可逆卡诺热泵的最优性能[J]. 厦门大学学报, 1984, 23(4): 414-419.

[10] Goth Y, Feidt M. Optimal COP for endoreversible heat pump or refrigerating machine [C]. C. R. Acd. Sc. Pairs, 1986, 303(1): 19-24.

[11] 陈林根, 孙丰瑞, 陈文振. 两源间制冷机有限时间火用 经济性能界限和优化准则[J].科学通报, 1990,35(23):1837.

[12] 陈林根, 孙丰瑞, 陈文振. 两源制冷机的生态学优化准则[J]. 自然杂志, 1992, 15(8): 633.

[13] Wu C. Specific heating load of an endoreversible Carnot heat pump [J]. Int. J. Ambient Energy., 1993, 14(1): 25-28.

[14] Chen L, Wu C, Sun F. Heat pump performance with internal heat leak [J]. Int. J. Ambient Energy., 1997, 18(3): 129-134.

[15] Sun F, Chen W, Chen L, Wu C. Optimum performance of an endoreversible Carnot heat pump [J]. Energy Convers. Mgmt., 1997, 38(14): 1439-1443.

[16] Chen L, Sun F, Wu C. Effect of heat transfer law on the performance of a generalized irreversible Carnot refrigerator. J. Non-Equibri. Thermodyn., 2001, 26(3): 291-304.

[17] Chen L, Zhu X, Sun F, Wu C. Exergy-based ecological optimization for a generalized irreversible Carnot heat pump. Applied Energy, 2007, 84(1): 78-88.

[18] Zhu X, Chen L, Sun F, Wu C. Exergy based ecological optimization for a generalized irreversible Carnot refrigerator. J. of Energy Institute., 2006, 79(1): 42-46.

[19] Zhu X, Chen L, Sun F, Wu C. Effect of heat transfer law on the ecological optimization of a generalized irreversible Carnot heat pump. Int. J. Exergy., 2005, 2(4): 423-436.

[20] Sahin B, Kodal A, Yavuz H. Maximum power density analysis of an endoreversible Carnot heat engine [J]. Energy, The Int., 1996, 21(10): 1219-1225.

[21] Erbay L B, Sisman A, Yavuz H. Analysis of Ericsson cycle at maximum power density conditions. ECOS96, 1996: 25-27.

[22] Chen L, Lin J, Sun F, Wu C. Efficiency of an Atkinson engine at maximum power density. Energy Convers. Mgmt., 1998, 39(3/4): 337-341.

[23] Chen L, Zheng J, Sun F, Wu C. Power density analysis and optimization of a regenerated closed variable-temperature heat reservoir Brayton cycle. J. Phys. D: Appl. Phys., 2001, 34(11): 1727-1739.

[24] Yavuz H L, Erbay L B. General performance Characteristics of an Ericsson refrigerator [C]. ECOS98, Nancy, France, 1998: 565-571.

[25] Erbay L B, Yavuz H. The maximum cooling density of a realistic Stirling refrigerator [J]. J. Phys. D: Appl. Phys., 1998, 31(3): 291-293.

[26] Zhou S, Chen L, Sun F, Wu C. Cooling load density analysis and optimization for an endoreversible air refrigerator [J]. Open Systems & Information Dynamics., 2001, 8(2): 147-155.

Optimization of Output Load Density for Reservoir Endoreversible Carnot Refrigerator and Heat Pump

Yang Guangming, Zhu Chaofeng, Liu Yunhai
(Navy Deputy Office in No.438 Factory, Wuhan 430061,China)

The performance analysis and optimization of constant-temperature heat reservoir endoreversible Carnot refrigerator and heat pump is carried out by taking the output load density（the ratio of output load to the maximum specific volume in the cycle）, i.e. the cooling load density and the heating load density as the optimization objective in this paper. The analytical expression for the optimal allocation of heat-exchanger area is derived. The effect of heat reservoir temperature ratio on the output load density is analyzed by detailed numerical examples. The results obtained are different from those with the cooling load and heating load objective and of theoretic significance to the design practice for future plants.

endoreversible Carnot refrigerator; endoreversible Carnot heat pump; cooling load density; heating load density

TB651

A

1003-4862（2015）04-0058-04

2014-12-10

杨光明（1982-），男，工程师。研究方向：电力电子技术。。