一种提高HWS采样率的透镜式微扫描方法

马辰昊，付跃刚

引言

哈特曼－夏克波前传感器（HWS）是一种在波前测量时常用到的仪器，目前已经广泛应用在光学系统装调，激光光源质量测量，空间光通信以及自适应光学等领域。哈特曼－夏克波传感器对波前的复原精度和测量时的动态范围限制了其应用，因此，大量科研人员在提高其测量精度方面展开了多方面的研究，在光斑质心识别、波前重构算法、微透镜设计等方面做了很多创新性的改进，但是也相应地增加了对波前检测的复杂程度［1－2］。

国外方面，研究人员2003年开始探索哈特曼－夏克传感器的算法及其应用。R.M.Clare等人详细地讨论了哈特曼传感器的成像原理并计算出斜率方程［3］。利用仿真软件仿真了斜率方程的线性区间。随后应用傅里叶光学的基本原理，得到波前形式，用于遗传算法的迭代初始方程，进一步完善了传感器的波前复原效果［4］。2007年，西班牙科学家Ramos提出了如何用波前像差和距离测量相位的方法［5］，在field－programmable gate array上用波前复原算法验证了理论结果的可行性［6］。国内方面，2002年，李新阳等人使用Zernike拟合方法，基于圆孔径内的波像差的测量推导出Zernike模式法波前重构算法的基本计算公式，并利用实验数据进行验证分析［7］。杨华峰等人于2005年提出了采用Zernike模式法对哈特曼传感器测量波前进行重构计算，针对19单元的哈特曼进行测量和数值模拟［8］。2011年，田爱玲等人提出将基于施密特正交法应用到哈特曼传感器测量原理上，通过利用Zernike波前重构，对参考波前和被测波前进行分析［9］。通过对国内外研究现状分析，科学工作者基本上都是在软件上提高对哈特曼传感器的波前复原精度。其中在算法上，虽然提高了波前复原精度，但是计算量普遍偏大，计算有所重复，在实验结果中产生了难以消除或不可消除的噪声。在硬件上通过减小哈特曼传感器微透镜的尺寸来提高采样率，以此来提高检测精度的难度较大，并且此方法会产生较高的成本。

通过上述分析，利用微扫描装置使被测波前产生微小位移，通过对不同位移的波前进行采样，再通过微扫描图像重建、波前复原的方法复原出被测波前，提高了哈特曼－夏克传感器的分辨率。设计了二维2×2模式下透镜式微扫描哈特曼传感器，利用多帧扫描图像的重构算法，通过对比实验，证明利用微扫描技术可以提高哈特曼－夏克传感器波前复原精度。

1 微扫描原理

微扫描技术是一种较成熟的提高成像系统空间分辨力的技术，已在很多领域得到应用，它通过使用微扫描装置对光路进行微量偏移，通过对相邻数帧在x或y方向上位移1／N（N为整数）个像素距的欠采样图像进行采集，得到N×N帧欠采样图像，之后利用相应算法对N×N帧欠采样图像进行图像重建，重建出一幅更高采样率的图像。

微扫描技术是一种常用的减少频谱混淆的方法，可以提高采集图像分辨率，一个采集数字图像的过程就是一个CCD或CMOS等成像探测器对被采集图像进行抽样的过程，从抽样定理中可知，对于一个带限图像，想要复原出原始图像则需要使抽样频率高于图像Nyquis频率的2倍以上。但实际对图像采集时一般抽样频率都要低于Nyquist频率的2倍，它会导致采集到的图像信号产生频谱混叠，影响采集图像的质量。微扫描的方法就可以在不提高探测器性能的情况下减少由图像抽样带来的影响。

2 应用于哈特曼传感器的微扫描技术分析

哈特曼－夏克波前传感器（HWS）是一种在对波前检测时常用到的仪器，被测波前经过光路缩束系统缩束后照射到微透镜阵列上，由微透镜阵列将输入的波前分割成若干个子波面，各子波面分别经由微透镜会聚到CCD探测器上，通过对CCD采集到的光斑分布图计算出光斑质心的偏离量，从而求出各子波面的波前斜率，最后复原出入射到微透镜阵列上的波前的形状［10］。

提高哈特曼传感器的测量精度与其微透镜阵列的性能密不可分，采用微扫描技术可以提高采样频率，得到高分辨率的图像。微扫描技术就是对一组具有微小位移差别的场景进行重复采样，得到多幅具有互补信息的低分辨率欠采样图像，通过对多幅欠采样图像按照采样时的顺序交叉像素点，重建出一幅新的图像。利用微扫描图像重构技术，可以在不改变成像系统的前提下，达到提高图像空间分辨率的目的。

2.1 哈特曼－夏克传感器原理

哈特曼－夏克传感器工作原理如图1所示，当入射波面是理想的平面波时，CCD得到的光斑阵列是与微透镜阵列完全对应的规则光斑阵列，如图1（a）所示；若入射波面是畸变波前时，CCD上得到的光斑将偏离理想位置，形成不规则的光斑阵列，如图1（b）所示，这些光斑与理想位置的偏离量代表了各个子波面的斜率，通过对波前斜率的计算就可以复原出入射波面［11］。

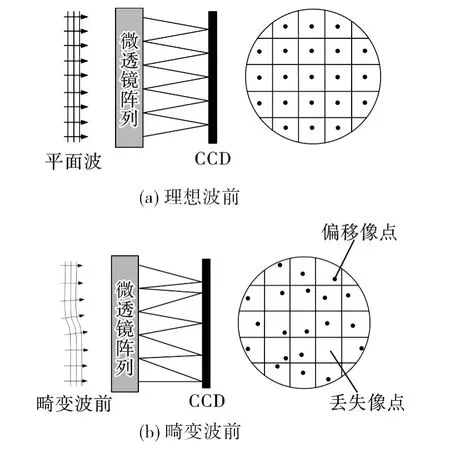
图1 哈特曼－夏克波前传感器探测原理示意图Fig.1 Principle of Hartmann－Shack wavefront sensor

2.2 微扫描技术原理

二维2×2微扫描提高微扫描空间分辨率的原理如图2所示，在CCD上与微透镜阵列完全对应地划分出各个子区域，将各个区域定义为一个像素组，如图2中的A、B、C、D所示。利用微扫描装置分别向着待测目标的右上、右下、左下、左上4个位置进行微量移动固定距离，2个位置间距离为微透镜尺寸的一半，取这4个位置为欠采样位置，通过CCD可以得到4幅低分辨率图像，如图2左侧所示，图像处理后将4幅欠采样图像重建为一幅高分辨率图像，如图2右侧所示。在整个过程中被测视场是保持不变的，因而理论上重建后图像的分辨率就是原图像的4倍［12］。

图2 微扫描提高空间分辨率的原理示意图Fig.2 Principle diagram for improving spacial resolution on micro－scanning

经过微扫描后的光斑分布图可以看作是一种图像信息。为了设置坐标系对图像进行分割，首先对由微扫描得到的欠采样光斑分布图进行大津阈值分割，减小背景噪声对中心识别的影响。之后对整帧图像采用迭代加权质心算法计算出该帧微扫描图像中光斑阵列的大致中心坐标（x0，y0）。利用基于局部最小二乘法的方法，在光斑分布图中心区域划分子区域，在其中寻找中心像点将其作为原点。在得到光斑分布图空缺点，即原点O之后，利用光斑图的整体信息和细节特点进行分块。分块的主要过程与每个光斑像素组的边框定位有关。已知哈特曼传感器的CCD像元尺寸为7.4μm×7.4μm，取每个像素组的大小为17像素×17像素，以原点O为中心，定义中心像素区域－8≤x≤8，－8≤y≤8为光斑分布图的像素组原点，以像素组原点为中心对整幅光斑图进行行方向和列方向分割，定义光楔旋转至315°位置时的光斑分布图为A组光斑分布图，光楔旋转至45°位置时的光斑分布图为B组光斑分布图，光楔旋转至135°位置时的光斑分布图为C组光斑分布图，光楔旋转至225°位置时的光斑分布图为D组光斑分布图，依次对A、B、C、D 4组欠采样光斑分布图的各自子像素组拼接完成后形成一幅新的光斑分布图。光斑质心识别算法是在由DeVries和K.L.Baker提出的迭代加权质心算法的基础上，加入了微扫描像素坐标变换后得到的。

本文采用的是透镜式微扫描，是通过一个机械装置控制扫描透镜进行微量移动，其原理示意图如图3所示，入射的一束平行光线经过透镜会聚后聚焦于焦平面上一点I，当透镜再垂直于光轴方向上向下移动一个微小距离d时，平行光束通过透镜聚焦于焦平面上一点I′，由几何关系可以算出2焦点I与I′之间的距离与透镜的微动距离d相等。

图3 透镜式微扫描原理示意图Fig.3 Schematic diagram of lens micro－scanning

2.3 基于透镜的微扫描控制系统

将微扫描透镜安装在一个由压电陶瓷控制的二维微动平台上实现二维微扫描。在扫描过程中，由于微扫描透镜的离轴偏移量很小，所以产生的像差可以忽略不计。基于透镜的微扫描装置与哈特曼传感器相结合的结构示意图如图4所示，微扫描透镜前是一个光路缩束系统，利用微扫描透镜将被测波前会聚到微透镜阵列上，微扫描透镜安装在一个二维微动平台上，通过驱动器对压电陶瓷输出电压产生微小位移，从而使被测波前产生移动。在控制过程中需要使微扫描的位移频率与哈特曼传感器的帧频同步，在二维2×2微扫描中，哈特曼传感器每采集一幅图像，微扫描透镜需移动L／2距离（微透镜尺寸为L），通过微扫描步长确定微扫描路线，微透镜阵列会聚的光斑分布图像将随着微扫描的进行在CCD探测器接收面上移动。

二维微动平台的精密定位控制系统主要由CPU、位置传感器及其测量电路、高压运放电路、数模转换电路及模数转换电路以及显示、控制、通信等接口电路组成。由CPU控制高压运放电路输出电压驱动压电陶瓷，使其产生微小位移。通过传感器采集位移信号，由测量电路进行信号处理，处理后的结果通过总线发送给CPU，经CPU计算、分析后对驱动模块进行相应控制，压电陶瓷微动装置的控制系统工作原理框图如图5所示。

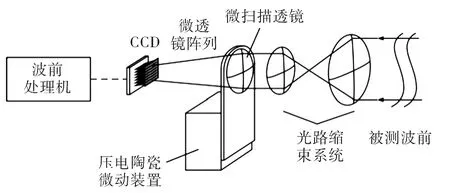
图4 透镜式微扫描哈特曼传感器结构示意图Fig.4 Structural diagram of lens micro－scanning in Hartmann－Shack sensor

图5 压电陶瓷微动装置控制系统工作原理框图Fig.5 Working principle diagram of PZT ceramics fretting device control system

3 实验结果及分析

实验选用哈特曼传感器的微透镜材料为融石英、形状为方形的抛物面平凸透镜，单个微透镜尺寸为0.13mm×0.13mm，透镜数为37×28个，可探测区域4.8mm×3.6mm，焦距为18.6mm，工作波段为974nm，测量速率为50Hz。

实验前先消除由扫描透镜引入的波前倾斜，右下、左下、左上4个方向分别偏移L＝45.96μm的4个位置采集到的4帧光斑分布图如图6（a）～图6（d）所示，透镜不进行偏移时光斑分布图如图6（e）所示。利用加入透镜微扫描的哈特曼－夏克波前传感器对同一待测光学系统的波前进行测量，透镜向右上、

图6 透镜式微扫描的哈特曼传感器对待测光学系统的波前进行测量的光斑分布图Fig.6 Spot distribution diagrams of measured optical system wavefront in lens micro－scanning Hartmann－Shack sensor

对采用透镜扫描得到的4帧光斑分布图利用2×2微扫描重建算法，重建后的光斑分布图如图7所示。

图7 2×2微扫描重建后的光斑分布图Fig.7 Spot distribution diagram of micro－scanningreconstruction on 2×2 mode

由图6（e）和图7的光斑分布情况可以得出2个系统中各个子光斑质心的偏移量，通过偏移量计算出2个系统对被测波前的复原情况，为评价被测波前复原情况，分别计算加入双光楔微扫描前后，哈特曼传感器入射波前与复原波前的相位平均值φ和方均根值RMSx：

式中：φc为第c个点的相位值；b为相位采样点的个数。

波前残差可表达为

式中：φr，c为第c个点的复原相位值；φi，c为第c个点的原始相位值。

波前相位残差均方根RMSD与原始波前相位均方根RMSφ的比值即为对波前的复位精度指标，用J来表示：

不采用微扫描的哈特曼－夏克传感器波前复原精度评价指标J＝0.092 1，采用透镜微扫描的哈特曼传感器波前复原精度评价指标J1＝0.065 3，复原精度提高百分比为

上述结果验证了采用二维2×2透镜式微扫描的哈特曼传感器对波前复原精度高于传统的哈特曼传感器对波前复原精度。

4 结论

文中提出了将哈特曼传感器与透镜式微扫描技术相结合的波前探测方法，结合多帧微扫描图像重构和波前重构计算分析，验证了所设计的透镜式微扫描哈特曼传感器可提高波前复原精度，实验得到被测光学系统的波前复原精度提高了41%。这种采用透镜微扫描装置的哈特曼－夏克传感器在对波前探测方面有很好的应用前景。

［1］ Zhang Jinye，Li Song，Zhou Hui，et al.New testing

method for cone prism based on Hartmann－shack wavefront sensor［J］.Journal of Applied Optics，2008，29（1）：136－140.

张金业，李松，周辉，等.一种基于哈特曼传感器的角锥棱镜检测方法［J］.应用光学，2008，29（1）：136－140.

［2］ Zhang Jinping，Zhang Zhongyu，Zhang Xuejun，et al.Algorithm for extending dynamic range of Shack－Hartmann wavefront sensor［J］.Acta Optica Sinica，2011，31（8）：140－144.

张金平，张忠玉，张学军，等.增大夏克哈特曼波前传感器动态范围的算法研究［J］.光学学报，2011，31（8）：140－144.

［3］ Clare R M，Lane R G.Comparison of wavefront sensing using subdivision at the aperture and focal planes［J］.Palmerston North，2003，187－192.

［4］ Clare R M，Lane R G.Phase retrieval from subdivision of the focal plane with a lenslet array［J］.Applized.Optics，2004，43：4080－4087.

［5］ JoséM R R，Fernando R G，JoséG M.Wavefront aberration and distance measurement phase camera：European，1983318A1［P］.2008－10－22.

［6］ Rodríguez－Ramos J M，CastellóE M，Conde C D，et al.2D－FFT implementation on FPGA for wavefront phase recovery from the CAFADIS camera［J］.SPIE，2008，7015：701539－1－11.

［7］ Li Xinyang，Jiang Wenhan.Zernike modal wavefront reconstruction error of Hartmann－Shack wavefront sensor［J］.Acta Optics Sinica，2002，22（10）：1236－1240.

李新阳，姜文汉.哈特曼—夏克传感器的泽尼克模式波前复原误差［J］.光学学报，2002，22（10）：1236－1240.

［8］ Yang Huafeng，Jiang Zongfu.Research of Zernike modal wavefront reconstruction of 19－element Hartmann－Shack wavefront sensor［J］.Laser Technology，2005，29（5）：484－487.

杨华峰，姜宗福.对Zernike模式法重构19单元哈特曼测量波前的研究［J］.激光技术，2005，29（5）：484－487.

［9］ Tang Guomao，He Yumei，Liao Zhou.Radial Hartmann method for measuring large optical system［J］.Chinese Journal of Lasers，2010，37（3）：795－799.

汤国茂，何玉梅，廖周.大型光学系统径向哈特曼像质检测方法［J］.中国激光，2010，37（3）：795－799.

［10］Kou Songfeng，Liu Genrong，Niu Dongsheng，et al.Design of Song Shack－Hartmann optical system［J］.Journal of Applied Optics，2014，35（1）：1－6.

寇松峰，刘根荣，牛冬生，等.“宋”望远镜夏克哈特曼光学系统设计［J］.应用光学，2014，35（1）：1－6.

［11］Cheng Liqun，Wang Xiaoman，Jing Wenbo.Centroid detection of Shack－Hartmann wave－front sensor by marked watershed method［J］.Optics and Precision Engineering，2014，22（6）：1494－1499.

程利群，王晓曼，景文博.利用标记分水岭法实现夏克－哈特曼波前传感器质心探测［J］.光学精密工程，2014，22（6）：1494－1499.

［12］Li Hui，Wu Yuntao，Pan Fan，et al.Study on electrically tunable Shack－Hartmann wavefront sensor based on liquid crystal［J］.Acta Optica Sinica，2013，33（12）：290－297.

李晖，吴云韬，潘凡，等.基于液晶电控可调夏克－哈特曼波前传感器的研究［J］.光学学报，2013（12）：290－297.

［13］Peng Fulun，Feng Zhuoxiang.Effect of micro－scanning on spatial resolution［J］.Journal of Applied Optics，2006，27（5）：394－399.

彭富伦，冯卓祥.微扫描对空间分辨率的影响［J］.应用光学，2006，27（5）：394－399.