跳步自回归模型在中长期日长变化预报中的应用∗

刘庆彬 王琪洁雷孟飞

(中南大学地球科学与信息物理学院长沙410083)

跳步自回归模型在中长期日长变化预报中的应用∗

刘庆彬 王琪洁†雷孟飞

(中南大学地球科学与信息物理学院长沙410083)

利用自回归模型进行日长变化中长期预报时,预报精度逐渐降低.跳步自回归模型在中长期的预报中具有良好的预报精度,且具有较好的预测稳定性.因此,尝试采用跳步自回归模型替代自回归模型进行日长变化预报.最后,利用国际地球自转参数与参考系服务(International Earth Rotation and Reference Systems Service,IERS)提供的EOP 08 C04日长变化序列进行实验,并分析比较两种模型的预报结果.实验结果表明,跳步自回归模型用于改善自回归模型中长期预报精度是可行有效的.

天体测量,时间,方法:数据分析

1 引言

地球自转速率变化即日长变化(Length of Day,LOD)是表征地球自转运动的一个重要参数,与极移、岁差和章动统称为地球定向参数(Earth Orientation Parameters, EOP).EOP是地球坐标系与天球坐标系之间相互转换的重要参数,并且在深空探测、卫星导航以及地球动力学研究等领域,也有重要的作用[1].现代空间测量技术,如甚长基线干涉(VLBI)、人卫激光测距(SLR)、全球定位系统(GPS)等,能够得到高精度及高分辨率的EOP数据.然而,由于复杂的数据处理过程,EOP结果难以实时获取,因此,高精度的EOP短期预报显得尤为重要,而对EOP的中长期预报的需求也日益增长[2].

关于日长变化的预报,国内外学者提出了许多预报方法:最小二乘外推与自回归组合模型(LS+AR)[3]、卡尔曼滤波(Kalman Filtering)[4−5]、人工神经网络(ANN)[6−8]、广义回归神经网络(GRNN)[9−11]、模糊小波变换[12]、门限自回归模型(TAR)[13]以及这些方法的改进模型与组合模型[14−16]等.地球定向参数预报比较计划(Earth Orientation Parameters Prediction Comparison Campaign,EOP PCC)的结果表明,没有一种预报方法能够使任意跨度的所有EOP预报精度达到最优;LS+AR模型在EOP预报模型中相对稳定,预报精度较高[17].AR模型结构简单,参数估计和定阶都比较容易,任何可逆的自回归与滑动平均(ARMA)模型都能采用高阶的AR模型以任意精度逼近[18],因此, LS+AR模型被广泛应用于日长变化预报.

LS+AR模型实质上是两步预报,即用LS外推预报趋势项和用AR模型预报残差项,两者之和即为最终预报值.然而,在中长期预报中,AR模型预报精度逐渐降低,针对这个问题,本文尝试采用跳步自回归(Leap-Step AutoRegression,LSAR)模型替代AR模型,对残差项进行预报.LSAR模型是由郑大伟等人首次提出的,其主要特点是采用了跳步时间序列分析(Leap-Step Time Series Analysis,LSTSA)模型,该模型的目的是为了改善数据处理分析过程中资料序列的端部效应,并取得了良好的效果[19−22].后来,郑大伟等证明了LSTSA用于资料序列预测时,在长期预报方面比其他的时间序列预报模型具有更好的效果,而且还具有较好的预测稳定性,若用样本密集的资料序列,其预测效果将会更加显著[23−25].因此,LSAR模型用于改善日长变化的中长期预报精度在理论上是可行的.为验证上述方法的可行性,本文将利用IERS提供的EOP 08 C04日长变化序列进行实验,并将结果与AR模型进行比较.

2 预报模型

2.1 最小二乘外推模型

在进行日长变化预报时,首先要扣除周期为5 d∼18.6 yr的62个固体地球带谐潮引起的日长周期性变化[26].这些扣除潮汐影响的日长变化称为LODR,下文中的日长变化预报都针对LODR进行.然后对LODR建立最小二乘外推模型[27]:

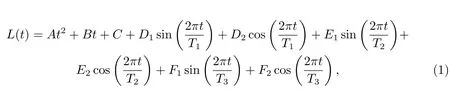
式中,A、B和C表示LODR序列的长趋势项参数;D1和D2表示LODR序列的周年项参数;E1和E2表示LODR序列的半周年项参数;F1和F2表示LODR序列的1/3周年项参数;T1、T2和T3分别表示周年摆动周期、半周年摆动周期以及1/3周年摆动周期,在拟合中取值分别为T1=1,T2=1/2,T3=1/3;t为时间,在拟合过程中单位换算为yr.

2.2 LSAR模型

设有平稳资料序列zn(n=1,2,···,N),则跳步时间序列模型为:

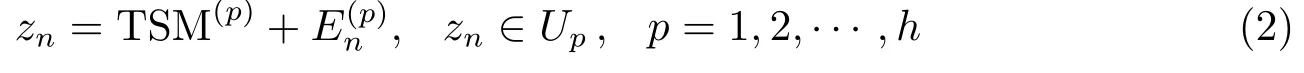
式中,Up为时间序列zn的第p个跳步域,若有序列zn的样本数N=h×m,则存在zp+(h×k)∈是序列zn属于第p个跳步域内n时刻的白噪声.TSM表示某种时间序列分析模型,当给定zn∈Up时,在跳步域Up内则可根据时间序列分析的理论和方法来建立TSM(p)模型.

本文中,对每个跳步域Up内的,我们采用AR模型.AR模型描述如下[28]:

式中,φi(i=1,2,···,k)为模型系数,αn为零均值白噪声,k为模型阶数.

AR建模预报时,最重要的是要确定AR模型的阶数.常用的定阶准则有终预误差准则(FPE)、信息论准则(AIC)和传递函数准则(CAT)3种,这3种准则实际上是等效的,本文采用FPE准则来定阶.FPE准则:

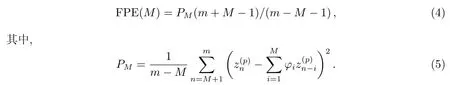
本文对LODR预报思路如图1所示:

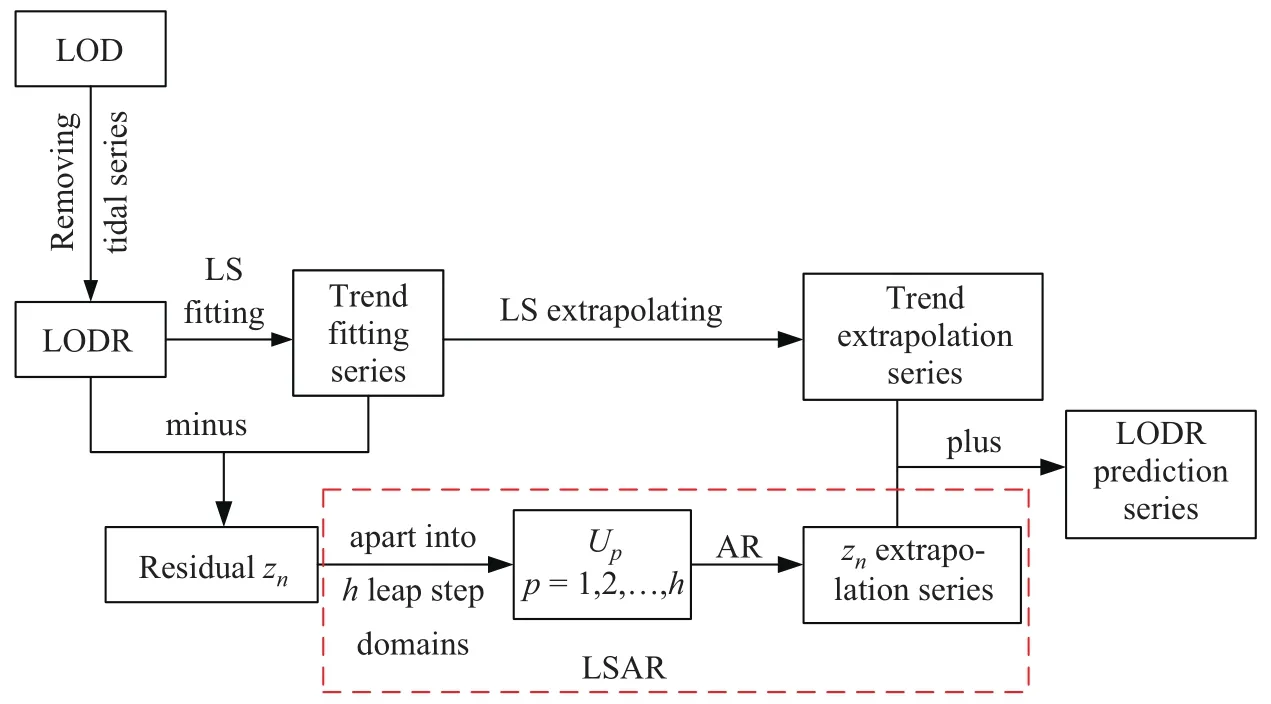
图1 LODR预报流程Fig.1 The process of predicting LODR

3 实验分析

本文实验数据来源于IERS提供的EOP 08 C04序列,选用2001年1月1日至2013年12月25日的日长变化序列,每日一值.其中,分别以2011年1月1日至2012年12月31日(共731个值)作为预报起点,依次往后预报360 d.

利用LSAR进行预报时,跳步域h取值的不同会影响预报精度.为选取合适的跳步域,分别令h=5,10,15,20进行实验,并统计跨度为1∼360 d的平均绝对误差(MeanAbsolute Error,MAE):

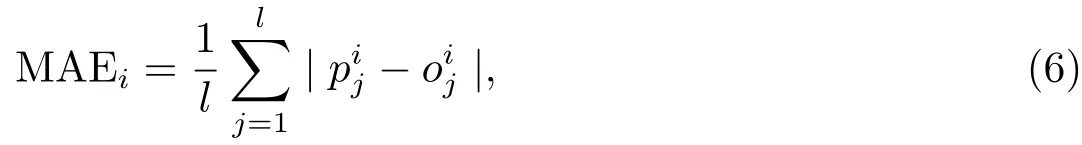
式中,o为观测值,p为预测值,i为预报跨度,l为预报长度.MAE反映的是预测误差绝对值的平均值,其结果如图2所示,其中实线表示h=5,虚线表示h=10,点线表示h=15,点划线表示h=20.从图2中我们可以看到,h=5与h=15预报精度相当,优于其余二者,但是在整体上,当h=5时,其预报精度最优,且随着跨度增大,优势愈加明显.这主要是因为h取值越大,每个跳步域内的样本间隔越大,从而影响预报精度,因此,在后续的实验中,我们均取h=5.

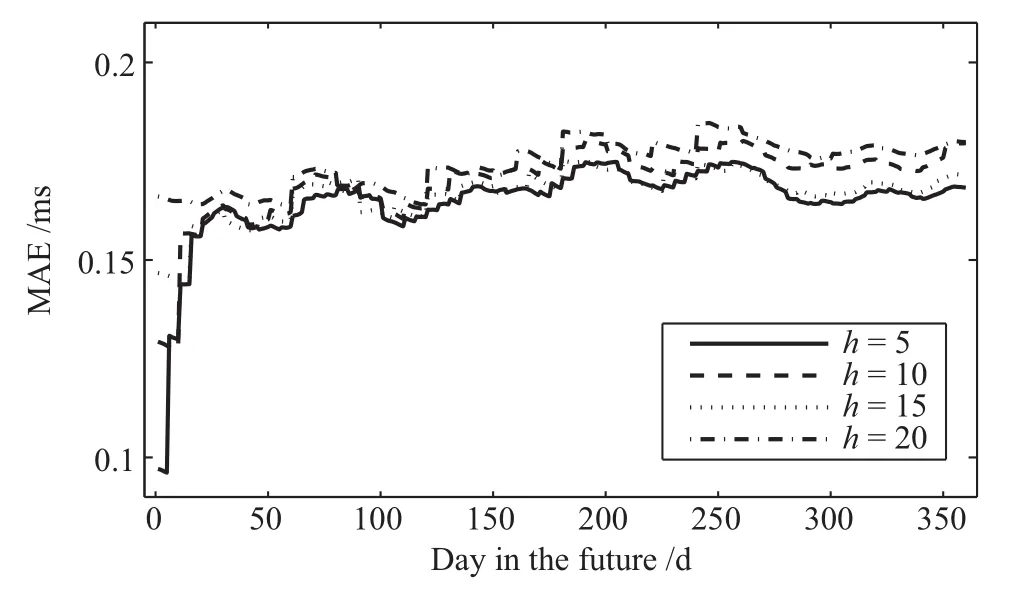
图2 不同跳步域MAE对比Fig.2 The comparison of MAE with di ff erent h

为验证LSAR模型在日长变化中长期预报上的有效性,分别应用LSAR模型与AR模型对LODR做跨度为1∼360 d的预报,与观测值对比,并统计二者的MAE,结果如表1与图3所示.

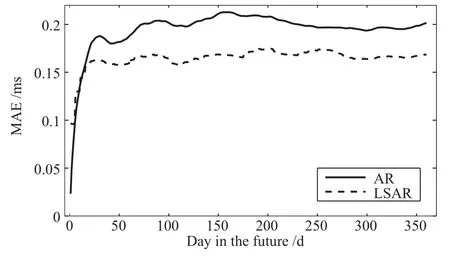
图3 LSAR模型与AR模型的预报精度(MAE)比较Fig.3 The comparison of MAE between LSAR and AR models

表1的第1、2、3列分别表示预报跨度、AR模型和LSAR模型的预报精度MAE,第4列表示LSAR模型相对于AR模型的预报精度提高百分比.图3中,AR模型用实线表示,LSAR模型用虚线表示.比较表1与图3可以看出,在10 d以内,LSAR模型预报精度略低于AR模型,但随着跨度的增大,LSAR模型的预报精度逐渐优于AR模型.跨度为10∼30 d的预报,精度改善在10%以内,从第30天开始,改善幅度比较明显,最大改善达19.62%(150 d),这证明了在日长变化的中长期预报中,LSAR模型相比于AR模型更具优势.

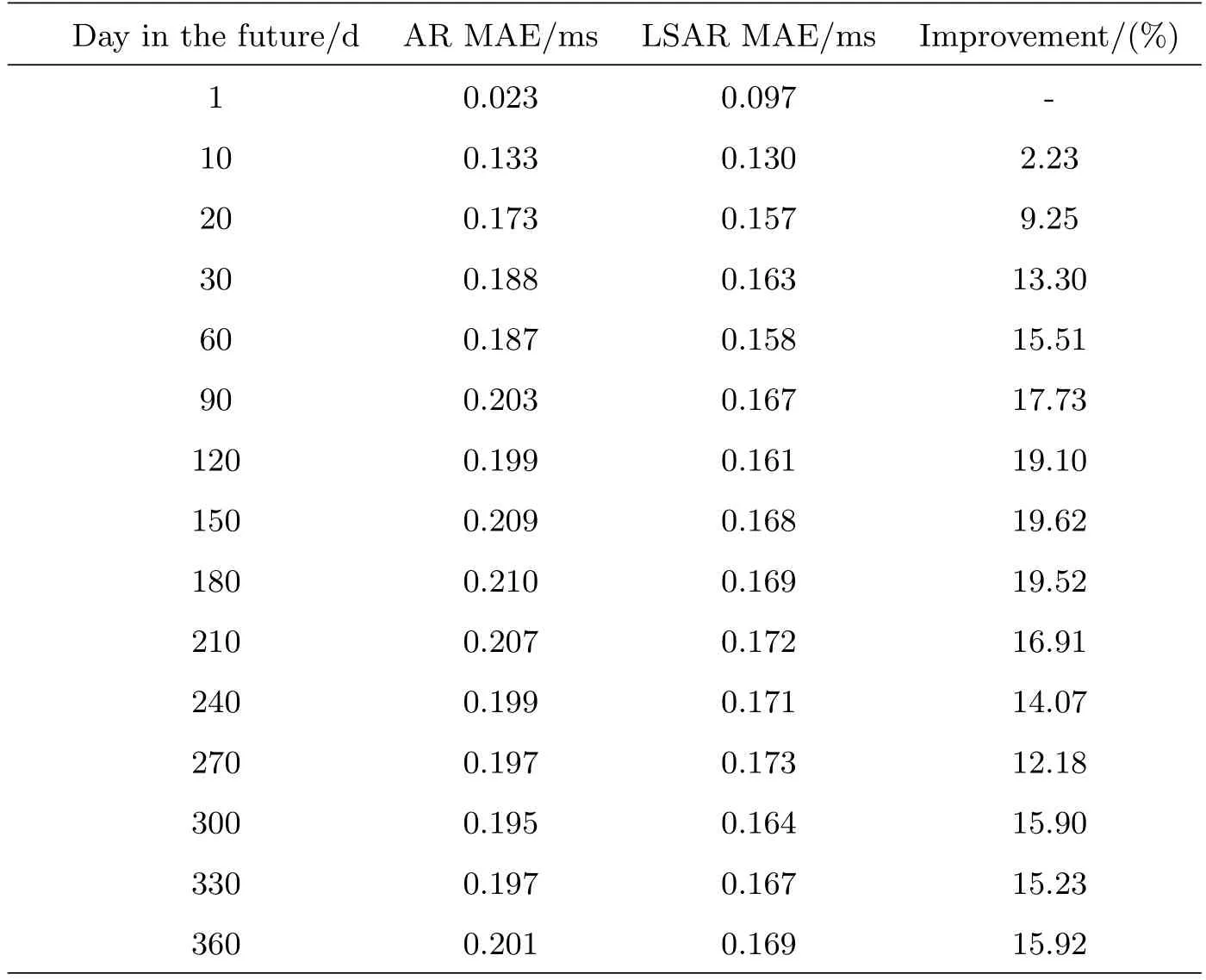
表1 LSAR模型与AR模型的预报精度(MAE)比较Table 1The comparison of MAE between LSAR and AR models

为了进一步证明LSAR模型在日长变化的中长期预报中优于AR模型,我们采用正规化均方误差(Normalized Mean Square Error,NMSE),对两种模型预报结果进行评定,比较结果见表2与图4.正规化均方误差:

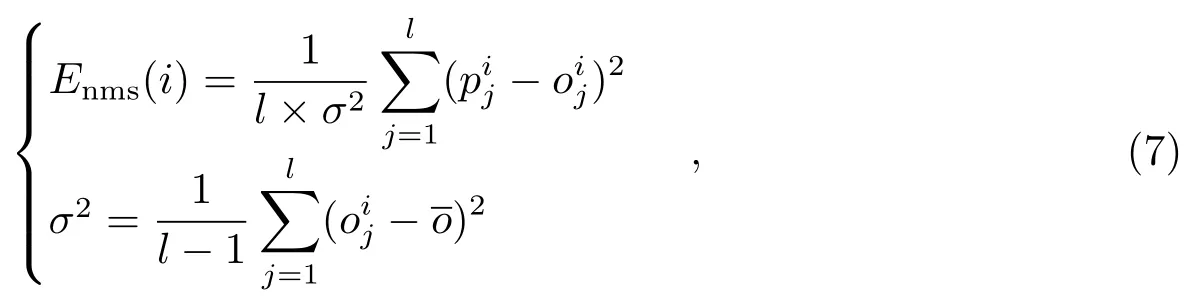
表2中,第1列为预报跨度,第2、3列分别为AR模型与LSAR模型预报精度NMSE,第4列为LSAR模型相对于AR模型预报精度提高百分比.图4中,实线表示AR模型,虚线表示LSAR模型.从表2及图4中可以发现,在10 d以内,LSAR模型预报精度略低于AR模型,但是随着跨度的增大,LSAR模型预报精度均优于AR模型,精度改善最大可达30.37%(180 d),这进一步证明了:相较于AR模型,LSAR模型在中长期预报中精度更高.

表2 LSAR模型与AR模型的预报精度(NMSE)比较Table 2The comparison of NMSE between LSAR and AR models

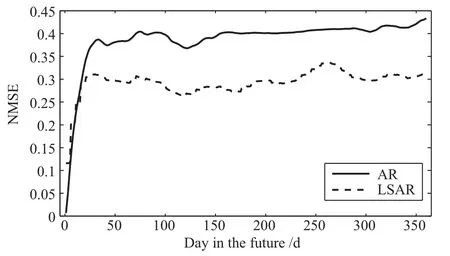
图4 LSAR模型与AR模型预报精度(NMSE)对比Fig.4 The comparison of NMSE between LSAR and AR models

4 总结与展望

本文针对LS+AR模型在日长变化的中长期预报中精度较低的不足,采用跳步自回归模型,即LSAR模型替代AR模型.实验结果表明,LSAR模型在10 d以内的预报中,精度略低于AR模型,但随着跨度的增大,LSAR模型预报精度逐渐优于AR模型,尤其在中长期预报中改善更加明显,证明了LSAR模型对于改善AR模型的中长期预报精度是可行有效的,这对于日长变化的预报具有一定的参考价值.

此外,大气角动量轴向分量与日长变化有着紧密的联系[30−31],在此后的研究中,将尝试将这二者结合进行预报.

[1]叶叔华,黄珹.天文地球动力学.济南:山东科学技术出版社,2000:478-479

[2]Su X Q,Liu L T,Houtse H,et al.JGeod,2014,88:145

[3]Kosek W,Kalarus M,Johnson T J,et al.ArtSa,2005,40:119

[4]Gross R S,Eubanks T M,Steppe J A,et al.JGeod,1998,72:215

[5]Karbon M,Nilsson T,Schuh H.EGU General Assembly 2013,2013,15:4984

[6]Schuh H,Ulrich M,Egger D,et al.JGeod,2002,76:247

[7]Wang Q J,Liao D C,Zhou Y H.ChSBu,2008,53:969

[8]Liao D C,Wang Q J,Zhou Y H,et al.JGeo,2012,62:87

[9]张晓红,王琪洁,朱建军,等.天文学报,2011,52:322

[10]Zhang X H,Wang Q J,Zhu J J,et al.ChA&A,2012,36:86

[11]Wang Q J,Du Y N,Liu J.Journal of Central South University,2014,45:1396

[12]Akyilmaz O,Kutterer H,Shum C K,et al.Applied Soft Computing,2011,11:837

[13]郑大伟,陈兆国.中国科学院上海天文台年刊,1982,4:116

[14]Guo J Y,Li Y B,Dai C L,et al.JGeo,2013,70:36

[15]刘建,王琪洁,张昊.武汉大学学报:信息科学版,2013,38:916

[16]Xu X Q,Zhou Y H,Liao D C.JGeo,2012,62:83

[17]Kalarus M,Schch H,Kosek W,et al.JGeod,2010,84:587

[18]An H Z,Chen Z G,Hannan E J.AnSta,1982,10:926

[19]董大南,郑大伟.中国科学院上海天文台年刊,1985,7:13

[20]郑大伟,董大南.天文学报,1986,27:368

[21]周永宏,郑大伟.中国科学院上海天文台年刊,1997,18:13

[22]Xu X Q,Zhou Y H,Dong D N.Proceedings of the Journ´ees 2013,2014:212

[23]郑大伟.天文学进展,1989,7:118

[24]郑大伟.中国科学院上海天文台年刊,1993,14:164

[25]郑大伟,虞南华.中国科学院上海天文台年刊,1996,17:36

[26]McCarthy D D,Luzum B J.BGeod,1991,65:18

[27]王琪洁.基于神经网络技术的地球自转变化预报.上海:中国科学院上海天文台,2007

[28]Box G E P,Jenkins G M.Time Series Analysis:Forecasting and Control.San Francisco:Holden-Day, 970:131-134

[29]丁月蓉.天文数据处理方法.南京:南京大学出版社,1998:295-296

[30]Yan H M,Chao B F.JGRD,2012,117:401

[31]王琪洁,廖德春,周永宏,等.天文学报,2008,49:93

Medium-and Long-term Prediction of LOD Change with the Leap-step Autoregressive Model

LIU Qing-bin WANG Qi-jie LEI Meng-fei
(School of Geosciences and Info-Physics,Central South University,Changsha 410083)

It is known that the accuracies of medium-and long-term prediction of changes of length of day(LOD)based on the combined least-square and autoregressive (LS+AR)decrease gradually.The leap-step autoregressive(LSAR)model is more accurate and stable in medium-and long-term prediction,therefore it is used to forecast the LOD changes in this work.Then the LOD series from EOP 08 C04 provided by IERS (International Earth Rotation and Reference Systems Service)is used to compare the e ff ectiveness of the LSAR and traditional AR methods.The predicted series resulted from the two models show that the prediction accuracy with the LSAR model is better than that from AR model in medium-and long-term prediction.

astrometry,time,methods:data analysis

P128

A

10.15940/j.cnki.0001-5245.2015.05.008

2015-01-28收到原稿,2015-04-10收到修改稿

∗国家自然科学基金项目(U1231105,U1531128,10878026)资助

†qjwang@csu.edu.cn