增量式数字PID参数整定的频域分析*

任震宇，段志荣，孙亚萍，李静（杭州师范大学钱江学院，浙江杭州310036）

增量式数字PID参数整定的频域分析*

任震宇，段志荣，孙亚萍，李静
（杭州师范大学钱江学院，浙江杭州310036）

增量式数字PID是自动控制系统优化过程中应用广泛的一种控制方法。分析了增量式PID参数调节对控制器性能以及系统环路性能的影响。MATLAB频域仿真结果表明，Kp、Kd、Ki值的改变直接造成PID控制器零点的位置发生移动，从而使得控制系统动态性能得到改善。

增量式数字PID；参数调节；频域分析

0 引言

计算机控制系统的核心是数字调节器，工程中常用的数字调节器控制方法有以下几种：（1）直接数字控制：根据采样理论和离散化后的数字模型设计数字控制器，该方法的前提是得到系统的数字模型；（2）比例-积分-微分（propotional-integral-derivative，PID）控制：调节器的输出是其输入的比例、积分和微分的函数，特点是不需要被控对象的数字模型，结构简单、稳定可靠，故工程应用广泛；（3）最优控制：基于性能指标J最小的控制策略（燃料最省、路径最短、时间最短），依赖于对象的数字模型；（4）智能控制：包括神经网络、模糊控制等，基于仿人类思维的模糊数据推理方法，不需要数字模型，但控制算法复杂。

1 增量式PID算法的数字实现

数字PID控制系统是时间的离散系统，Proportional（比例）、Integral（积分）、Differential（微分）可根据系统的要求，对输入的偏差按比例、积分和微分的函数关系运算得到控制量，输出到执行器完成相应的调节任务[1]。在PID调节中，由于PID算式可以灵活地改变其结构，因此选择不同的P、I、D会得到不同的控制效果，特别是当算法中某些参数选择不当时，会引起控制系统的超调或振荡，这对某些生产过程是十分有害的[2]。为了避免这种有害现象的发生，分析和研究PID算法，确定合理的PID参数是必要的，同时对PID控制技术的广泛应用具有重要的意义。

PID算法的模拟表达式如式（1）所示：

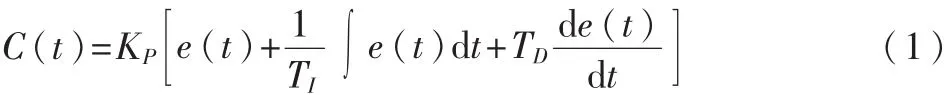
对积分项和微分项进行离散化：

将式（2）和式（3）代入模拟表达式中得到离散PID表达式：

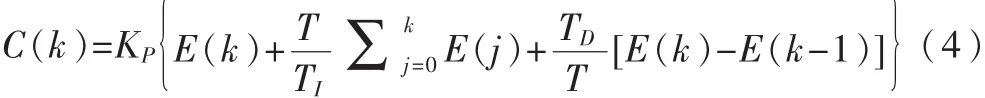
上式的输出与系统位置一一对应，也称为位置型PID算式。用位置型PID算式计算C（K），需要用到各采样时刻的偏差值，计算复杂，且需要占用内存。

对于系统（k-1）时刻的输出：

将式（4）、式（5）相减后得到如下表达式：

式（6）表示第k次输出的信号增量，称为增量型PID控制算式。

位置型算式不仅需要对E（j）进行累加，而且计算机的任何故障都将引起C（k）的大幅度变化，对生产不利。增量型较位置型的优点如下：（1）由于输出的是增量，所以误动作小；（2）易于实现手动/自动的无扰切换（位置型算法中，当由手动切换到自动时，首先需要保证控制器的输出等于实际的控制量；增量型算式只给出偏差，而与原来位置无关）；（3）不产生积分失控，容易获得良好的调节品质。

2 增量型PID参数调节对控制器的性能影响

对于增量型PID数字控制策略，为了便于分析其对系统性能的影响，将差分方程进行Z变换得到脉冲函数，如式7所示：

根据BackEuler公式：

得到增量型PID的S域传递函数模型：

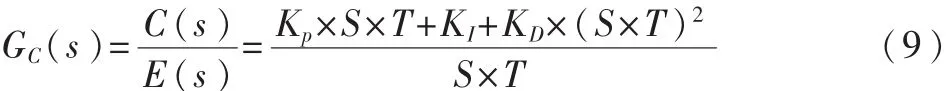
从校正系统的传递函数中可以简单地看出Kp、KI、KD、T均与控制器的零点相关。

2.1 Kp变化对幅值相位的影响分析

根据增量式PID的传递函数编写MATLAB命令如下：

kp=0.002*32*1023/3.3*2.49/10.36/3300；

ki=0.002*32*1023/3.3*2.49/10.36/3300；

kd=0.002*32*1023/3.3*2.49/10.36/3300；

fs=（150e3）；

a=tf（[kd/fs kp ki*fs]，[10]）；

a1=tf（[kd/fs kp*100 ki*fs]，[1 0]）；

a2=tf（[kd/fs kp/100 ki*fs]，[1 0]）；

bode（a，′-′，a1，′--′，a2，′.-′）；

a中Kp采用标准值，a1中Kp值增大为a中Kp值的100倍，a2中Kp值减小为a中Kp值的百分之一。MATLAB仿真画出PID校正装置相应的Bode图，如图1所示。

图1 Kp变化时PID控制器的Bode图

从图1可以明显看出，随着Kp增大，PID控制器两个零点逐渐分离，且起始增益无明显变化；反之，Kp减小，两个零点向中间靠拢。

2.2 KI变化对幅值相位的影响分析

MATLAB仿真时，a采用KI标准值，a1中KI值增大为a中KI值的100倍，a2中KI值减小为a中KI值的百分之一，相应的Bode图如图2所示。

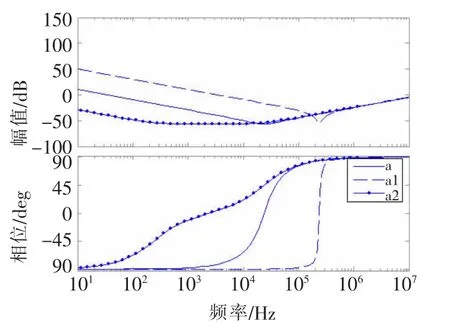
图2 KI变化时PID控制器的Bode图

从图2可以明显看出随着KI增大（a2→a→a1），零极点右移，左边零点右移，最终两个零点同时右移，起始增益明显增加；反之，KI减小（a1→a→a2），零极点左移，左边零点左移，起始增益明显减小。

2.3 KD变化对幅值相位的影响分析

MATLAB仿真时，a采用KD标准值，a1中KD值增大为a中KD值的100倍，a2中KD值减小为a中KD值的百分之一，相应的Bode图如图3所示。

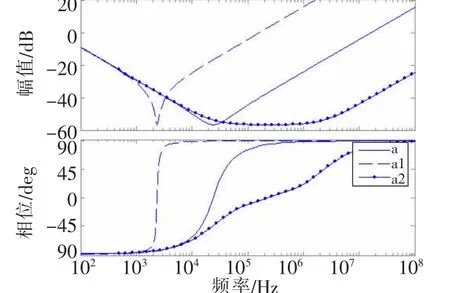
图3 KD变化时PID控制器的Bode图

从图3可以明显看出，随着KD增大（a2→a→a1），右边零点左移，最终两个零点同时左移，起始增益无明显变化；反之，KD减小（a1→a→a2），右边零点右移。

3 PID参数调节对系统稳定性能的影响分析

为了进一步分析PID参数调节对系统性能的影响，本文以Buck变换器在电阻性负载下的传递函数模型为例进行说明。

3.1 Buck变换器的小信号模型

Buck变换器闭环控制系统如图4所示。

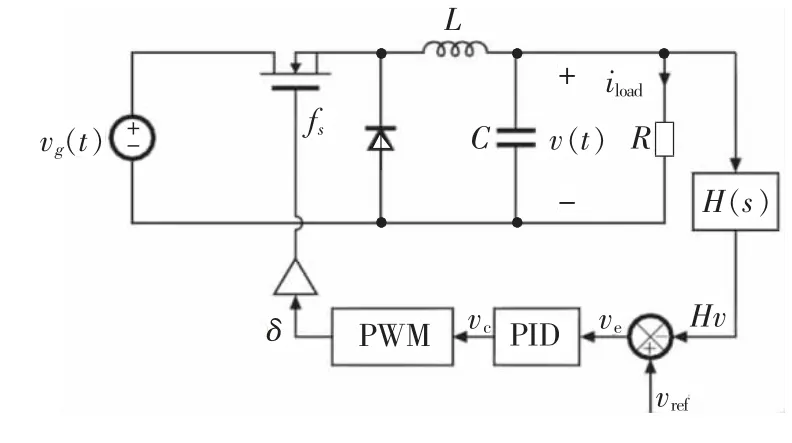
图4 Buck变换器闭环控制系统原理图

Buck变换器工作在连续电流模式（CCM）下，其小信号传递函数如式（10）所示：

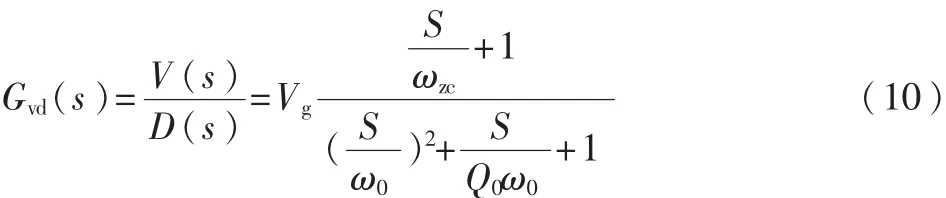
式中，Vg为系统的输入电压，为电容C的等效串联电阻RESR左半平面零点频率为二阶系统的左半平面双极点频率，为二阶系统的品质因数，RDCR为电感的直流电阻。传递函数的具体推导过程可参考文献[3]。

3.2 Kp变化对系统性能的影响分析

带PID控制器的Buck变换器系统的开环传递函数为：

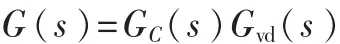
MATLAB仿真时，Buck变换器取如下参数：Vg=50/4 V，L=0.24μH，RDCR=0.7Ω，C=330μF，RESR=0.1 mΩ，R=10Ω；G采用Kp标准值，G1中Kp值增大为G中Kp值的10倍，G2中Kp值减小为G中Kp值的十分之一，仿真得到系统的Bode图如图5所示。

图5 Kp变化时Buck开环系统的Bode图

从图中可以明显看出，随着Kp减小（G1→G→G2），系统谐振峰值减小，有利于系统的平稳性，但系统相位裕量会减小甚至出现负值，从而导致系统不稳定。

3.3 KI变化对系统稳定性能的影响分析

G采用KI标准值，G1中KI值增大为G中KI值的10倍，G2中KI值减小为G中KI值的十分之一，仿真得到系统的Bode图如图6所示。

图6 KI变化时Buck开环系统的Bode图

从图中可以明显看出随着KI增大（G2→G→G1），系统相位裕量明显减小，并出现负值，导致系统不稳定，故在PID设计中KI系数虽然有利于消除静差，但仍不能取值太大。

3.4 KD变化对系统稳定性能的影响分析

G采用KD标准值，G1中KD值增大为G中KD值的10倍，G2中KD值减小为G中KD值的十分之一，仿真得到系统的Bode图如图7所示。

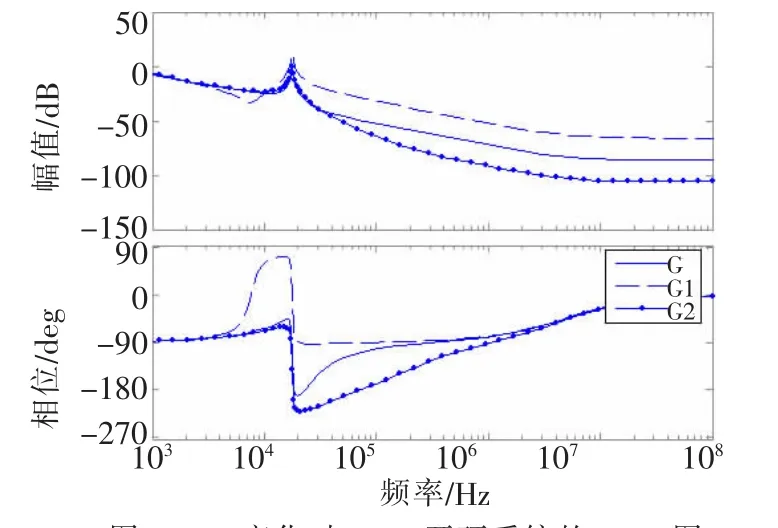
图7 KD变化时Buck开环系统的Bode图

从图中可以明显看出，随着KD减小（G1→G→G2），系统抗噪声能力增强，但相位裕量会出现负值，从而导致系统不稳定。

4 结论

通过以上对数字增量式PID控制算法的分析与研究，可得出PID参数调节对控制器本身性能的影响如下：

（1）Kp对增益影响不大，且Kp的增大导致两个零点频率分离。

（2）KI对低端增益有影响操控，因为KI增大，零极点频率增大。同时，KI增大，左边的零点右移，当左边的零点达到右边零点频率时，两个零点同时右移。

（3）KD对增益影响不大，且KD的增大导致右边零点左移，当右边的零点达到左边零点频率时，两个零点同时左移。

在对系统进行增量式数字PID校正过程中，系统的稳定性、快速性、平稳性以及准确性是相互矛盾、不能同时兼得的，故应根据实际情况合理选择Kp、KI、KD参数优化系统性能。尤其当Kp、KD变小或KI值增大时，系统相位裕量会出现负值，从而导致系统不稳定，在实际设计中应注意避免。

[1]胡寿松．自动控制原理[M]．北京：科学出版社，2013．

[2]刘光亚，彭维娜．PID参数性能分析及改进[J]．湖北工业大学学报，2013，28（1）：60-63．

[3]ERICKSON R W，MAKSIMOVIC D．Fundamentals of Power Electronics[M]．USA：Kluwer Academic Publishers，2001.

Frequency domain analysis of incremental digital PID parameter tuning

Ren Zhenyu，Duan Zhirong，Sun Yaping，Li Jing
（Qianjiang College，Hangzhou Normal University，Hangzhou 310036，China）

Incremental digital propotional-integral-derivative（PID）controller is commonly used in optimization of automatic control system.The influence of incremental PID parameter tuning for controller and closed-loop system is analysed.Based on the characteristic frequency of the PID controller and the corresponding simulation results，the zeros of system will moved by the change of PID parameters，and the system will have better dynamic character.

incremental digital PID；parameter tuning；frequency domain analysis

TP273

A

1674-7720（2015）03-0092-03

2014-09-03）

任震宇（1992-），男，本科在读，主要研究方向：电子信息工程。

浙江省科技厅重大科技专项重点工业项目（2012C01012-4）；浙江省大学生科技创新项目（2013R421049）

段志荣（1992-），女，本科在读，主要研究方向：电子信息工程。

孙亚萍（1980-），通信作者，女，硕士研究生，讲师，主要研究方向：电力电子研究，E-mail：ypsun2009@zju.edu.cn。