q-非广延分布等离子体中的离子声孤波∗

蔺福军廖晶晶 朱 云

(1江西理工大学理学院赣州341000)

(2江西理工大学应用科学学院赣州341000)

q-非广延分布等离子体中的离子声孤波∗

蔺福军1†廖晶晶2朱 云1

(1江西理工大学理学院赣州341000)

(2江西理工大学应用科学学院赣州341000)

从三维非广延分布函数及流体动力学方程组出发,研究了非广延分布等离子体中电子的非广延性对离子声孤波结构和性质的影响.通过理论解析获得Sagdeev赝势方程,从该方程出发研究了不同q所对应离子声孤波的振幅、宽度及电子数密度的空间分布.数值结果表明:离子声孤波存在的可允许范围由参量q决定,并且电子的非广延效应对离子声孤波的空间特性及电子密度分布均有较大影响.

星际介质:运动学与动力学,等离子体,波

1 引言

离子声孤波是等离子体中重要的非线性结构.1966年,Sagdeev[1]首次利用非线性理论研究了这类波的特性;随后,Ikezi等[2]在双等离子体装置中通过观测证实了离子声孤波的存在.自此之后,人们从理论[3−5]、实验[6−9]和粒子模拟(PIC)[10−13]等多方面对离子声孤波展开研究.Pakzad[4]通过理论解析研究了包括非热离子、电子、质子的等离子体中的离子声孤波,结果表明,非热电子对离子声孤波存在的参量空间有较大修正;Nagasawa等[7]在双等离子体装置中完成了离子声孤波反射与折射的实验观测; Sheridan等[11]模拟了大扰动演化为离子声孤波的过程,研究发现大振幅离声波最终能够衰减变为一个离子声孤波和一个离声波.需要说明的是,早期对非线性离子声孤波的研究大多是以麦克斯韦分布等离子体为对象.众所周知,麦克斯韦分布对处理宏观遍历性平衡系统是普遍有效的,但在处理有长程相互作用的等离子体系统及引力系统时失去优势[14−15].

为克服以上困难,Tsallis[14]将经典统计热力学中的熵推广至非广延空间并表达为Sq=kB(1−∑(q−1),其中pi是第i个微观态出现的概率;kB是玻尔兹曼常数;q是描述系统非广延性质的参量.对于微观态几率分别为A和B的两个独立非广延系统,它们的熵具有伪叠加性质,即Sq(A+B)=Sq(A)+Sq(B)+(1−q)Sq(A)Sq(B).基于此,Silva等[16]给出了q-非广延速度分布函数.人们利用非广延统计理论已成功解释了诸多天体现象,包括太阳中微子[17]、星系本体速度分布[18]以及具有长程相互作用和类不规则时空系统中的物理问题.近年来,非广延分布电子等离子体中孤波问题受到广泛关注.2011年,Pakzad[19]研究了弱相对论等离子体中非广延电子对非线性离子声孤波性质及结构的影响,结果表明,当非广延电子存在时,等离子体中只可能形成压缩性孤子,参量q对孤波结构有显著影响;2012年,Sahu[20]研究了包含非广延电子与热正电子的非磁化等离子体中离子声孤波及哨声波的非线性结构,结果显示,非广延电子对离子声孤波和哨声波的结构及性质均有影响;2013年,Shalini[21]研究了多温非广延分布电子对小振幅离子声孤波传播的影响,研究表明,电子的非广延性、电子与离子的比值以及温度比均显著影响离子声孤波结构及特征;Pakzad等[22]研究了含有非广延电子、热正电子及高相对论离子的等离子体中小振幅离子声孤波的传播特性,结果表明,相对论离子及非广延电子对离子声孤波的振幅和宽度均有影响.众多研究均已体现出非广延分布等离子体与麦克斯韦分布等离子体性质的差别.然而有部分研究处理过程有待商榷.Tribeche等[15]研究了双成分非广延分布电子等离子体中离子声孤波的性质,结果显示,离子声孤波的振幅及性质显著依赖于非广延参量q;Pakzad[23]探究了非广延电子对电子声孤波的影响,结果指出,非广延电子修订了电子声孤波存在的马赫数区间; Amour等[24]研究了非广延电子的存在对电子声孤波传播特性的影响,再次强调了非广延电子在电子声孤波形成过程中的重要性.但他们的工作是从一维平衡非广延分布函数及流体动力学方程出发的,然而一维平衡分布的定义不甚明确.本文假设所有参量只依赖于坐标x,将电子服从的三维非广延分布函数依次对坐标y和z积分,最终获得边缘分布函数,即适合描述准一维问题的分布函数.在此基础上重新考虑非广延电子对离子声孤波的影响,望对读者有所帮助.

2 理论模型和基本方程

考虑双成分(电子-离子)非广延电子等离子体,其平衡态(ϕ=0)满足准中性条件,即n0i=n0e=n0,下标“0”表示未扰态.众所周知,等离子体系统中的非线性效应使波形变陡,而线性色散效应则阻碍这种波动变陡,当两者可相比拟或在一特定方向上(纵向)能够精确补偿时,便形成稳定孤波.很显然,若出现横向运动,则要求非线性效应与线性色散需在各个方向彼此补偿,这几乎无法实现.为研究离子声孤波,本文假设所有场量均不依赖坐标y和z,即A(x,y,z)=(n,v,ϕ)=A(x).因此,描述空间离声运动的动力学控制方程可写为:

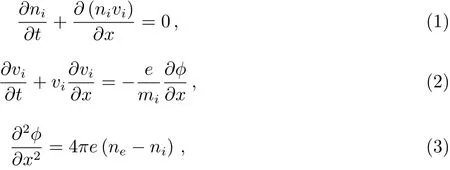
其中,ϕ=ϕ(x)是由于扰动速度vi引起电荷分离而产生的静电势;ni和ne分别表示离子和电子的数密度,其他物理量具有通常物理意义.

为描述电子非广延性的影响,文章从如下三维平衡非广延分布函数出发[16]:

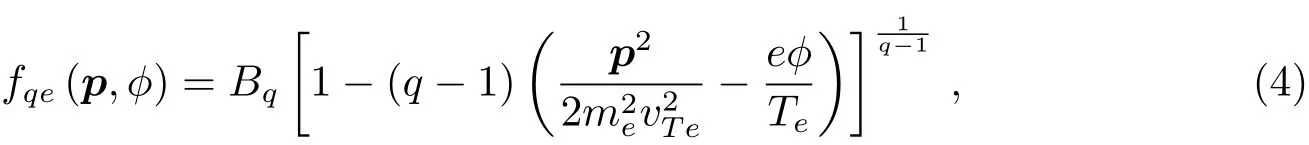
(4)式的归一化条件为

其中,

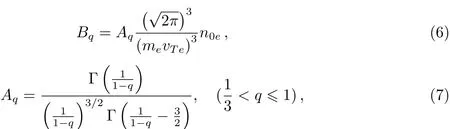
或

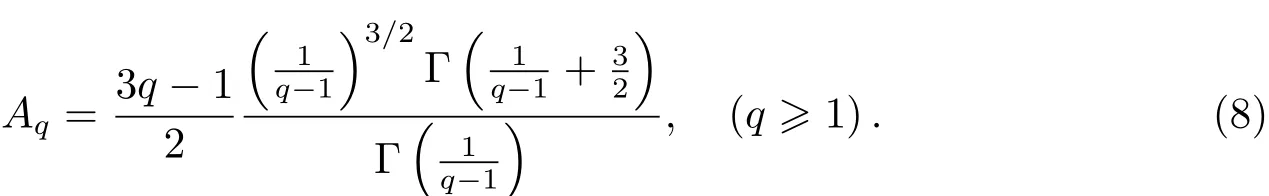
在广延极限下(q→1),分布函数(4)式能够回到熟悉的麦克斯韦-玻尔兹曼速度分布

为给出非广延区域的温度定义,Chen等[25]计算了非广延电子的平均动能,其表达为

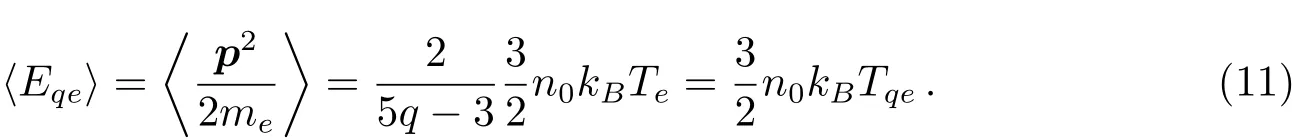
(11)式要求q＞3/5,其中Tqe=2Te/(5q−3)是非广延电子系统有效温度.

从方程(5)可得

这里,

是边缘分布函数,亦即,准一维分布函数.当3/5＜q＜1时,方程(13)可写为:

方程(14)的积分结果为(详见参考文献[25]):

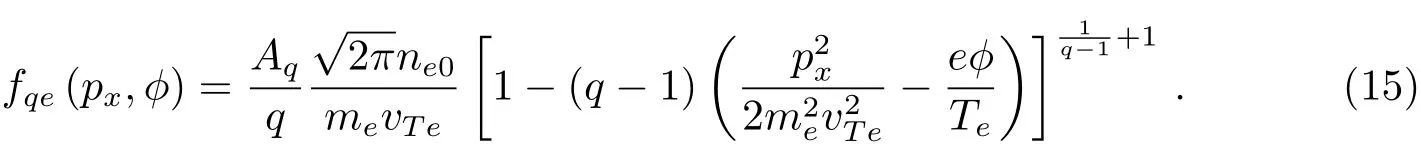
方程(15)已利用到积分公式[26]

其中,|argβ|＜π,p＞0,0＜Reµ＜pReν;B(···)是Beta函数,可表达为Gamma函数的形式[26]

类似地,对q≥1,方程(13)为

将方程(15)代入(12)中,并对px积分可得当时,

对q≥1,方程(19)依然成立.很显然,方程(19)与文献[15]中的方程(8)不尽相同,这种指数上的差异很大程度上能够影响函数的性质.产生这种差别的可能原因在于文献[15]中获得一维分布函数的过程中丢失了其他两维的信息,应该从三维分布函数出发,通过对py和pz积分获得准一维分布函数.

3 非线性分析与孤波解

引入无量纲参量:

λDe=[Te/(4πe2n0e)]1/2是徳拜长度;Cs=(Te/mi)1/2是离子声速;ωpi=(4πe2n0i/ mi)1/2是离子等离子体振动频率,方程(1)-(3)可改写为如下无量纲形式:

为研究等离子体中离子声孤波的传播特性,在此引入新变量ξ=X−MT′(M=孤波速度/Cs),则考虑到边界处方程(21)和(22)的积分结果分别为

和

联立方程(24)和(25),容易得到

考虑到方程(19)、(20)及(26),泊松方程(23)变为

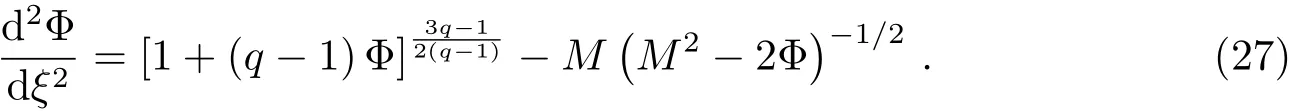
其中Sagdeev势

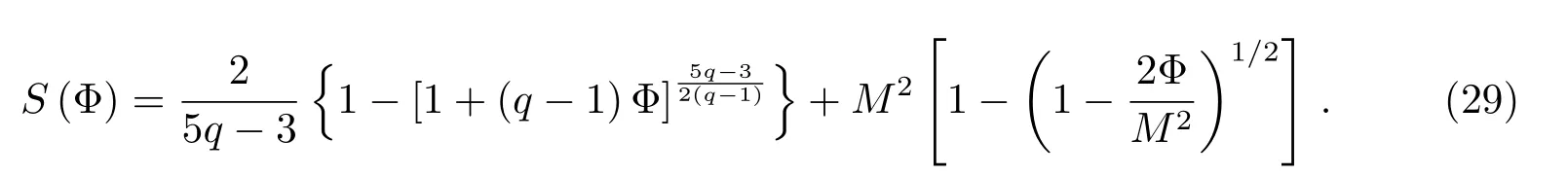
方程(28)具有能量积分的形式,左边第1项可看作为以速度dΦ/dξ运动的单位质量准粒子的动能,第2项相当于捕获准粒子的势场.方程(28)存在孤波解的条件为[1]:

(1)在Φ=0处,S(Φ)=S′(Φ)=0且S′′(Φ)＜0;

(2)存在非零解Φc满足S(Φc)=0;

(3)在0＜Φ＜Φc区间,S(Φ)＜0.

利用以上条件,可求得孤波存在所要求马赫数的范围.条件(1)要求

图1中,当3/5＜q＜1时,马赫数的下限大于玻尔兹曼分布情况(q=1);当q＞1时,情况相反,这提供了亚声速离子声孤波存在的可能性.马赫数的上限Mmax可由S(Φc)≥0确定,其中Φc=M2/2,此时离子数密度Ni是实数,由此给出:

数值解析方程(31)可得到马赫数的上限Mmax随q参量的变化曲线,如图2(a)(3/5＜q＜1)与图2(b)(q＞1).从图1及图2看出,非广延电子很大程度修正了离子声孤波存在所要求的马赫数范围.值得说明的是,图2(a)所示当3/5＜q＜1时马赫数的变化趋势与Tribeche等[15]的结果完全不同.

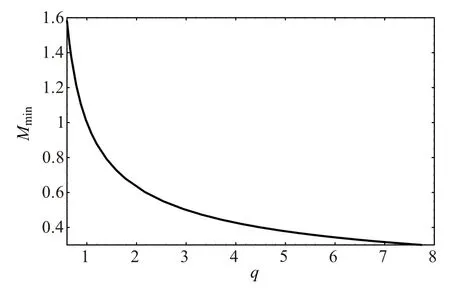
图1 电子非广延参量3/5＜q＜8时,马赫数下限Mmin的变化Fig.1 The variation of lower limitMminof the allowable Mach numbers with the nonextensiveq-parameter for 3/5＜q＜8

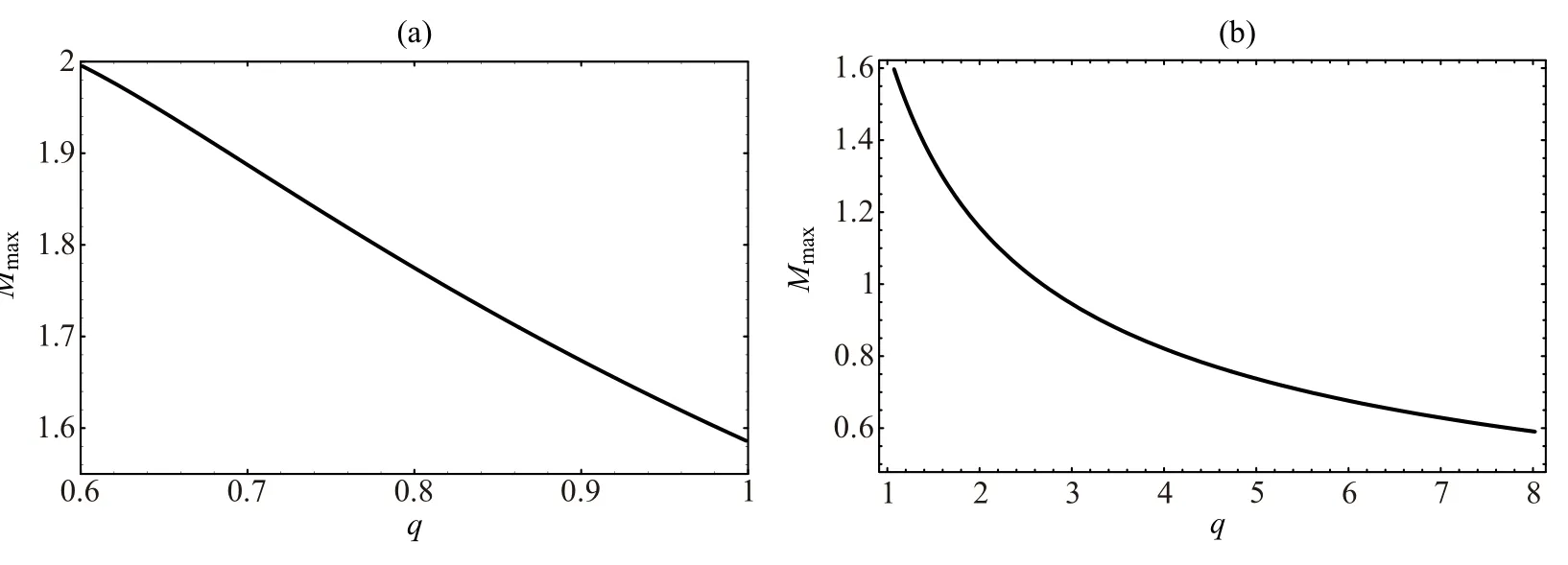
图2 3/5＜q＜1(a)和1＜q＜8(b)时马赫数上限的变化曲线Fig.2The variation of upper limitMmaxof the allowable Mach numbers with the nonextensiveq-parameter.(a)3/5＜q＜1 and(b)1＜q＜8

接下来在小振幅极限下求解方程(28).首先以Φ为变量展开S(Φ)并保留至三次项,则方程(29)可简化为:

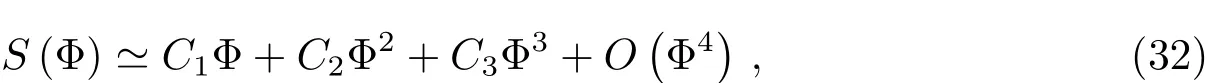
其中,

考虑方程(32)和(33),方程(28)的解可表示为:

式中,ΦM=−C2/C3和Δ=(−2/C2)1/2分别代表孤波的振幅及宽度.显然,在满足方程(30)及(31)时,孤波的宽度Δ随q增大而变窄,振幅ΦM随q的增加而变大.

4 数值计算及结果讨论

接下来数值研究非广延电子的存在对离子声孤波的影响.初始值选取为[15]: Φ|ξ=0=0以及(dΦ/dξ)|ξ=0=10−10.图3(a)描述了当M=0.75,q分别取2.2(点线)、2.3(实线)和2.4(虚线)时静电势Φ的空间变化.此参数选取满足方程(30)及(31),其对应的Sagdeev势S(Φ)由图3(b)给出.由图可知,电子非广延特性对亚声速离子声孤波的性质有显著影响,伴随着q参量的增加,孤波的振幅明显增大,同时宽度变窄.换言之,当电子分布逐渐偏离热平衡状态时,将会形成明显尖峰的离子声孤波结构;当M=1.2,q分别取0.89(点线)、0.90(实线)和0.91(虚线)时静电势Φ的空间变化及其对应的Sagdeev势S(Φ)分别由图4(a)和4(b)给出,图示表明,电子的非广延性对超声速离子声孤波的影响同样显著.与图3(b)比较,图4(b)中超声速离声压缩性孤波的振幅(由Sagdeev势曲线的宽度决定)大于亚声速情况,而孤波脉冲的倾斜程度(由Sagdeev势曲线的势阱深度决定)变小.图5(a)(参数与图3相同)和5(b)(参数与图4相同)描述了不同非广延参量q所对应电子数密度Ne的空间分布情况.图5表明,低q的电子绝大多数被排出至孤波区域之外,而高q电子聚集在狭小的空间区域.

图3 当M=0.75,q分别取2.2(点线)、2.3(实线)和2.4(虚线)时亚声速孤波(a)及相应S(Φ)(b)的空间变化Fig.3 The spatial variations of the subsonic ion-acoustic soliton(a)and the corresponding Sagdeev potentialS(ϕ)(b)forq=2.2(dotted line),2.3(solid line),and 2.4(dashed line),respectively,withM=0.75

图4 当M=1.2,q分别取0.89(点线)、0.9(实线)和0.91(虚线)时超声速孤波(a)及相应S(Φ)(b)的空间变化Fig.4 The spatial variations of the supersonic ion-acoustic soliton(a)and the corresponding Sagdeev potentialS(ϕ)(b)forq=0.89(dotted line),0.9(solid line),and 0.91(dashed line),respectively,withM=1.2

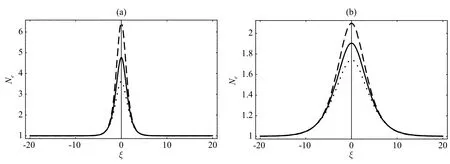
图5 不同非广延参量q所对应电子数密度Ne的空间分布情况.(a)中参数与图3相同,(b)与图4相同Fig.5 Spatial pro fi le of the electron densityNefor di ff erent values of the nonextensiveq-parameter,(a) with the same parameters as Fig.3,and(b)with the same parameters as Fig.4

采用Sagdeev赝势法重新研究了非广延分布等离子体中离子声孤波的特性.为研究孤子,文中假设所有的场量均不依赖于坐标y和z,从三维q-非广延分布函数出发,获得了电子数密度的具体表达式(19)式.利用流体动力学模型,理论解析得到了“能量积分”方程(28)和Sagdeev势S(Φ).数值计算结果表明,电子非广延性对离子声孤波的性质及存在区域有显著影响.对不同q值,离子声孤波存在所要求的马赫数范围Mmin＜M＜Mmax由图1～2给出,其提供了亚声速与超声速孤波存在的可能性.研究结果显示,非广延电子对离子声孤波的空间结构有较大修正,随着q值增加,孤波振幅明显增大,同时宽度相应变窄,出现高度非线性尖峰结构;另外,随着电子非广延参量q的增加,高q电子聚集在狭小的空间区域,形成强非线性结构.

致谢感谢南京师范大学博士生导师李晓卿教授在本论文完成过程中的指导和帮助;感谢匿名审稿人针对本论文不足之处提出的宝贵意见.

[1]Sagdeev R Z.RvPP,1966,4:23

[2]Ikezi H,Taylor R,Baker D.PhRvL,1970,25:11

[3]Abdelsalam U M,Moslem W M,Shukla P K.PhRvA,2008,372:4057

[4]Pakzad H R.PhLA,2009,373:847

[5]Rasheed A,Tsintsadze N L,Murtaza G.PhPl,2011,18:112701

[6]Lonngren K E,Chen C,Khazei M.PhLA,1981,85:33

[7]Nagasawa T,Nishida Y.PhRvL,1986,56:2688

[8]Yi S,Bai E W,Lonngren K E.PhPl,1997,4:2436

[9]Yi S,Lonngren K E.PhPl,1997,4:289

[10]Sheridan T E.PhLA,1997,235:253

[11]Sheridan T E,Yi S,Lonngren K E.PhPl,1998,5:3165

[12]Honzawa T.PhFl,1984,27:1013

[13]Choi C R,Ryu C M,Rha K C,et al.PhPl,2012,19:032105

[14]Tsallis C.JSP,1988,52:479

[15]Tribeche M,Djebarni L,Amour R.PhPl,2010,17:042114

[16]Silva Jr R,Plastino A R,Lima J A S.PhLA,1998,249:401

[17]Kaniadakis G,Lavagno A,Quarati P.PhLB,1996,369:308

[18]Lavagno A,Kaniadakis G,Rego-Monteiro M,et al.ApL&C,1998,35:449

[19]Pakzad H R.Ap&SS,2011,334:337

[20]Sahu B.Ap&SS,2012,338:251

[21]Shalini N S S.Ap&SS,2013,346:155

[22]Pakzad H R,Javidan K.InJPh,2013,87:705

[23]Pakzad H R.PhyS,2011,83:015505

[24]Amour R,Tribeche M,Shukla P K.Ap&SS,2012,338:287

[25]Chen X C,Li X Q.PhRvE,2012,86:068401

[26]Gradshteyn I S,Ryzhik I M.Table of Integrals,Series,and Products.5th edition.New York:Academic Press,1996:235

Ion-acoustic Solitary Waves in aq-nonextensive Plasma

LIN Fu-jun1LIAO Jing-jing2ZHU Yun1
(1 School of Science,Jiangxi University of Science and Technology,Ganzhou 341000)
(2 College of Applied Science,Jiangxi University of Science and Technology,Ganzhou 341000)

Based on the three-dimensional nonextensive distribution function and hydrodynamic equations,the e ff ects of nonextensive electron distribution on the structures and properties of ion-acoustic solitary waves have been studied.It is analytically derived an equation involving the Sagdeev-type pseudo-potential,which is used to study the amplitude and width of ion-acoustic solitary waves,and the spatial distribution of electron number density with di ff erent nonextensive parameterq.The numerical results suggest that the allowable domain where the ion-acoustic solitary waves may exist is determined byq,and the spatial pro fi le of the ion-acoustic solitary waves and electron density distribution are signi fi cantly a ff ected by the electron nonextensive e ff ects.

ISM:kinematics and dynamics,plasmas,wave

P142;

A

10.15940/j.cnki.0001-5245.2015.01.003

2014-07-06收到原稿,2014-08-05收到修改稿

∗国家自然科学基金理论物理专项基金项目(11377153)、江西省教育厅科学技术基金项目(GJJ14464)、江西理工大学科研基金重点项目(NSFJ2014-K17)、江西理工大学博士启动基金项目(jxxjbs13024)、江西理工大学应用科学学院科研基金项目(YJ2014-11)及江西理工大学科研基金一般项目(nsfj2014-g26)资助

†fujun012@yeah.net