EGUP与黑洞熵的修正值∗

白吉龙 温廷敦

(中北大学理学院物理系太原030051)

EGUP与黑洞熵的修正值∗

白吉龙 温廷敦†

(中北大学理学院物理系太原030051)

目前,人们对黑洞Bekenstein-Hawking熵的量子修正值产生了极大的兴趣,尤其是黑洞熵对数修正项的系数.在广义不确定关系(GUP)的基础上,通过引入了推广的广义不确定关系(EGUP),运用面积定理计算了3类时空的黑洞熵的修正值,得到的黑洞熵的修正项的系数是正的.这种计算方法不仅对单视界时空适用,而且对有内视界的黑洞时空依然成立,并且在EGUP基础上计算出黑洞熵的修正值.相比GUP基础上得到的黑洞熵, EGUP可以应用于大尺度时空下,所以应用范围更广.此计算方法简洁明了,物理意义明确,可为黑洞熵对数修正值系数的确定提供参考.

黑洞物理学,引力,恒星:黑洞,宇宙大尺度结构

1 引言

从20世纪70年代Bekenstein提出黑洞视界和它的熵成正比之后[1−2],黑洞热力学的研究取得了很大的成就,但是对于黑洞熵的起源问题还不清楚.为此人们提出了各种求黑洞熵的方法,比如Hooft提出的Brick-Wall方法以及之后改进的薄层模型,弦理论和单圈量子引力理论等[3].最近对于黑洞熵修正值的研究[3−6],也是热点之一,通过不同的方法求得的黑洞熵的修正值,都得到了不少有价值的结论.对于研究黑洞熵,必须考虑到黑洞的量子效应,就是说当黑洞吸收和辐射粒子时必须考虑海森堡不确定关系,但是在黑洞这样的强引力场中必须对原本的海森堡不确定关系进行修正,用广义不确定关系(GUP)取代[7],以确保态密度方程在视界附近收敛.近年来,在GUP基础上计算黑洞熵得到了广泛的研究[8−11],把GUP引入态密度方程来计算黑洞Dirac场熵[12−13],以及通过GUP并运用WKB近似法计算黑洞标量场的熵[14−17].而在大尺度下,在广义不确定关系的基础上,人们引入了推广的广义不确定关系(EGUP)来计算黑洞熵的修正值[18].

本文在计算中认为Benkenstein-Hawking定理在推广的广义不确定关系下仍然成立,我们给出的方法对具体的时空没有要求.本文对3类具有代表性的黑洞时空进行了探讨,分别为Schwarzschild黑洞,Gar fi nkle-Horowitz-Strominger dilaton黑洞以及具有双视界的Reissner-Nordstrom黑洞.

2 推广的广义不确定关系

由于我们考虑的黑洞辐射是量子效应,则能量为Δ≈cΔp的粒子就应当满足海森堡不确定关系:

其中xi和pj分别为空间坐标和动量,ħ为约化普朗克常数,δij为克罗内克函数.而在引力场中应当引入修正项,修改为广义不确定关系[19]:

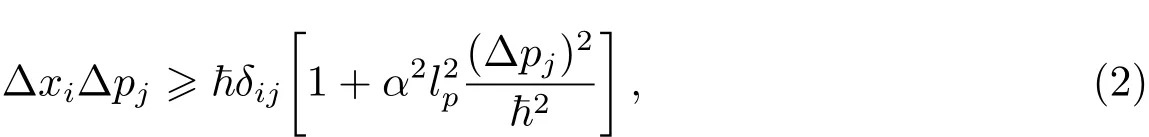
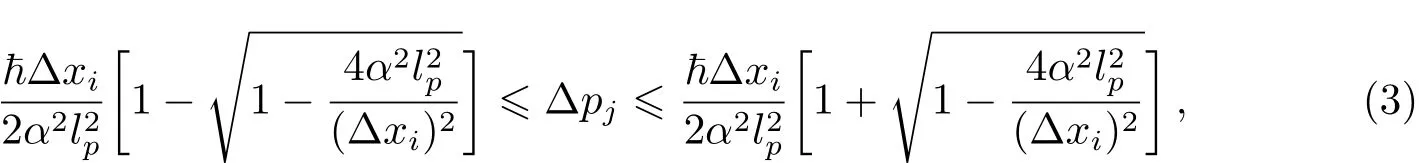
不等式(3)式的左边可以展开为Taylor级数[3],

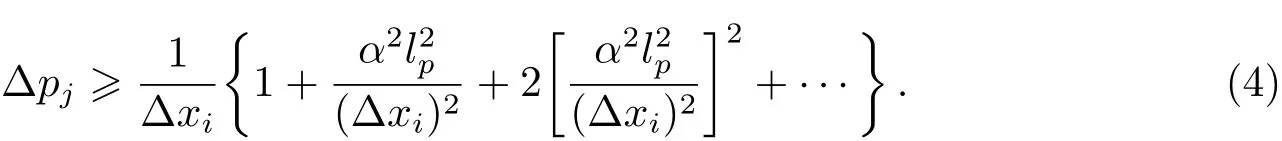
在广义不确定关系的基础上,根据时空对称性理论,可以得到[20−22]:

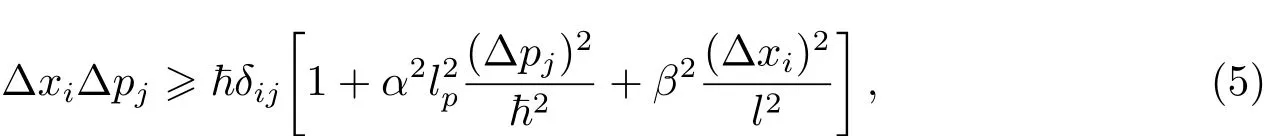
这里l是一个拥有大尺度的量,β是一个常数参量,和具体的时空有关,由上式可得:

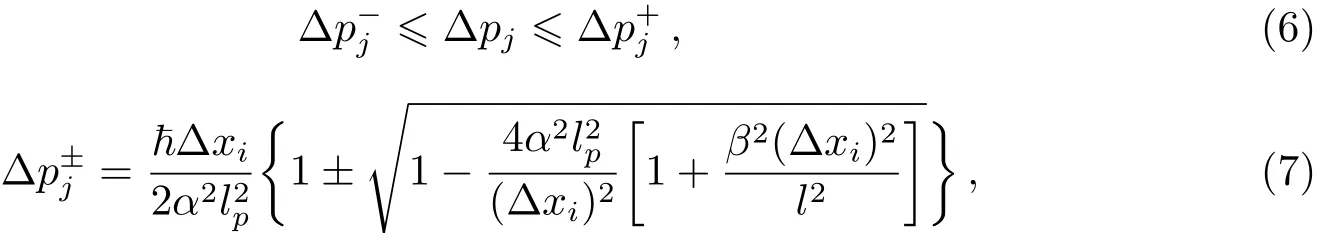
和

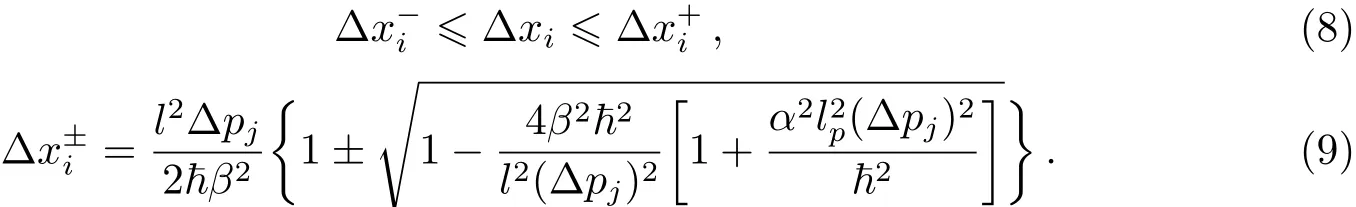
和广义不确定关系相比,EGUP同时拥有位置和动量不确定度的最小值如下:

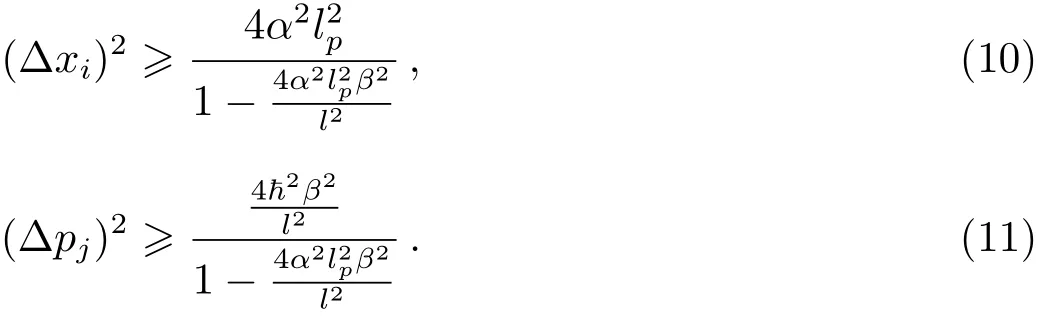
不等式(6)式的左边给出了海森堡不确定关系的修正值,如果存在关系则有:

根据上式即可推导黑洞熵的修正值.下面我们通过(12)式来计算3类黑洞的修正熵.

3 Schwarzschild黑洞

Schwarzschild黑洞时空线元为:

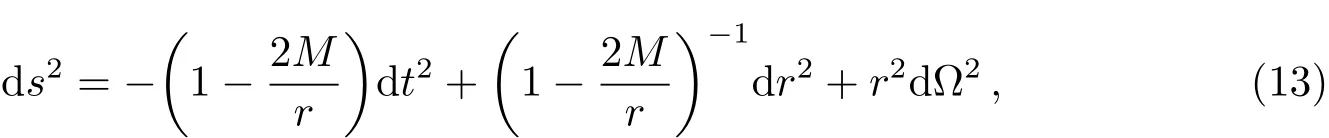
其中Ω为立体角,M为黑洞的质量.Hawking辐射的温度T、黑洞视界面积A和黑洞熵S分别为:

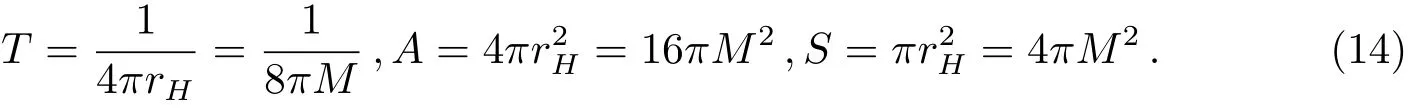
式中rH=2M是Schwarzschild黑洞视界的位置.

当黑洞吸收(或者辐射)一个能量为ΔM的粒子,则黑洞视界面积的增量(或者减小量)为:

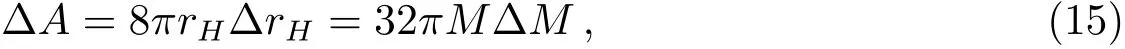
由于我们考虑的黑洞辐射是量子效应,则由(1)式和(15)式可得到黑洞视界面积的变化如下:

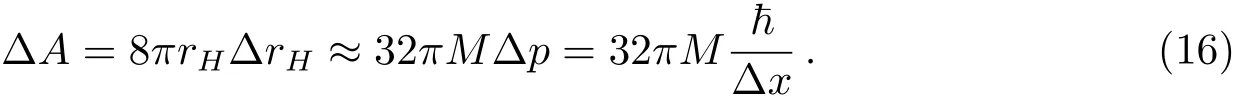
由推广的广义不确定关系(12)式和(15)式可知,黑洞视界面积的变化可表示为:

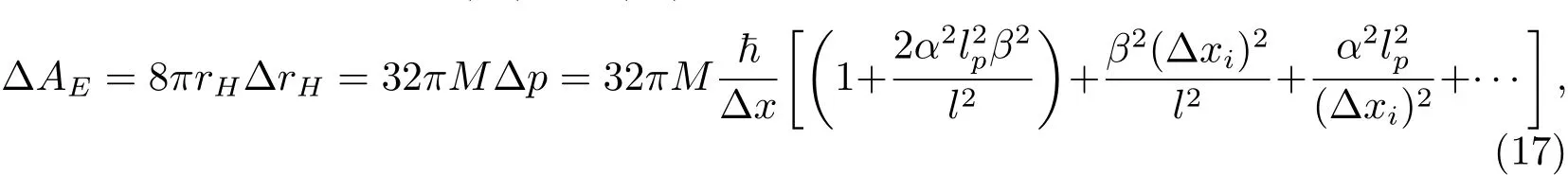
则由(16)式和(17)式可得:

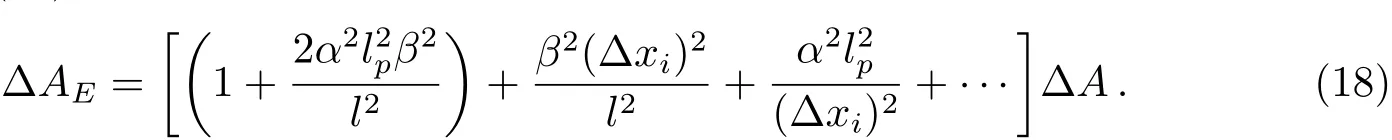
考虑到关系[3,23]:

将(19)式代入(18)式并积分可得:

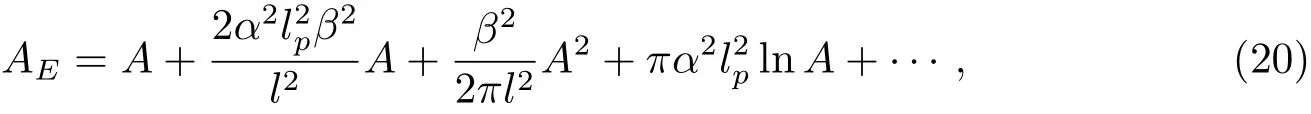
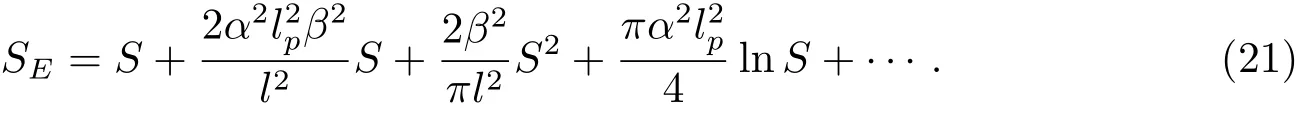
式中S即为Bekenstein-Hawking熵,结果显示修正项有1阶、2阶和对数项,而且这些修正项系数皆为正,由于l是拥有大尺度的量,所以1阶修正项和2阶修正项要比S小.

4 Gar fi nkle-Horowitz-Strominger dilaton黑洞

Gar fi nkle-Horowitz-Strominger dilaton黑洞时空线元为[24−25]:

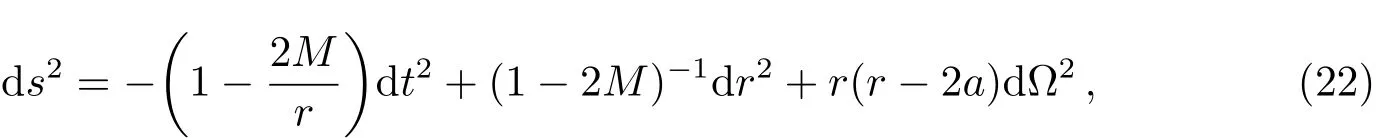
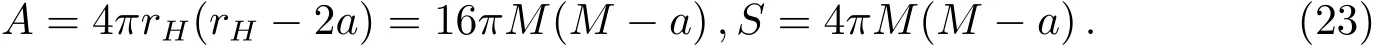
在a不变的情况下,我们可以得到:

在考虑了EGUP后,可得:

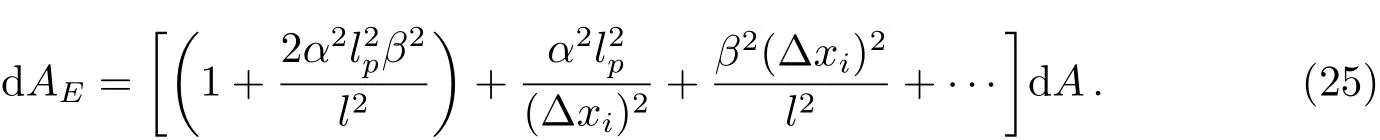
取Δx=2rH,则上式可写为:

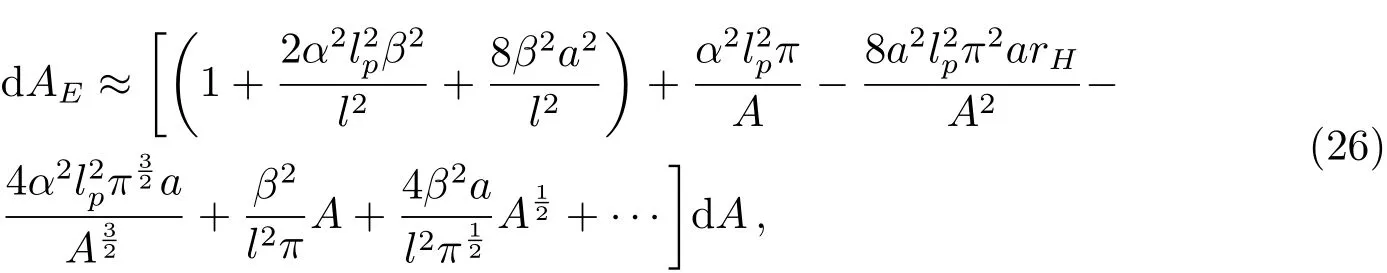
积分可得:

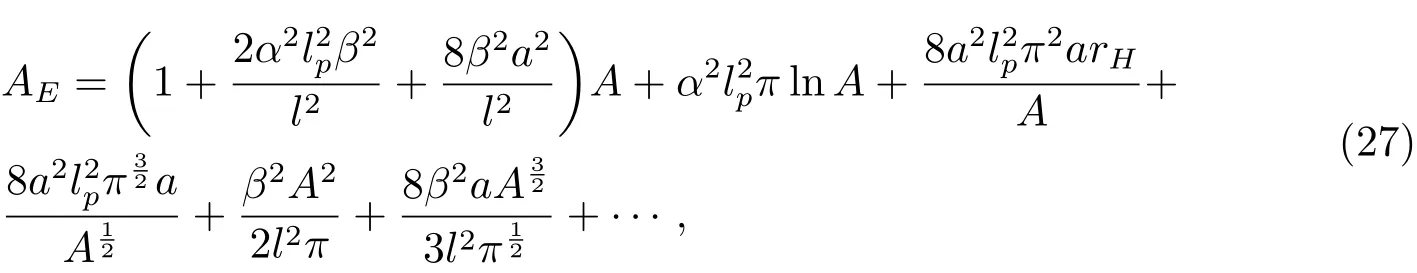
在上式计算中应用了a≪rH.根据Bekenstein-Hawking面积定理,即可得到考虑了EGUP后熵的表达式,即熵的修正式:

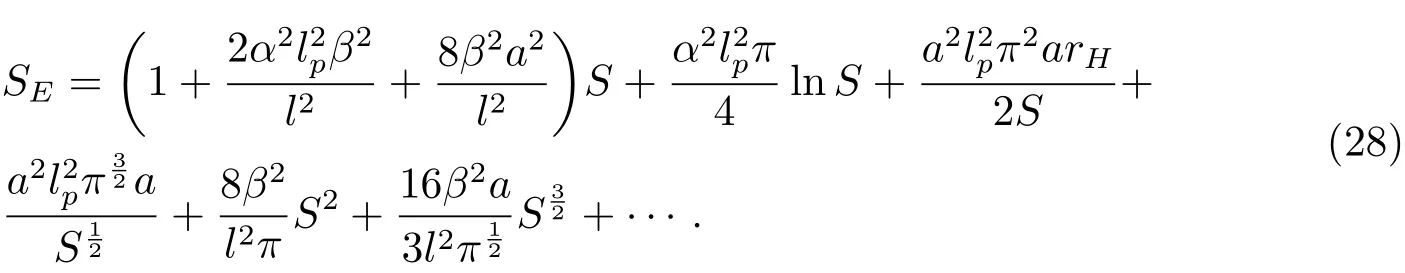
上式中S即为Bekenstein-Hawking熵.

5 Reissner-Nordstrom黑洞

Reissner-Nordstrom黑洞时空线元为:

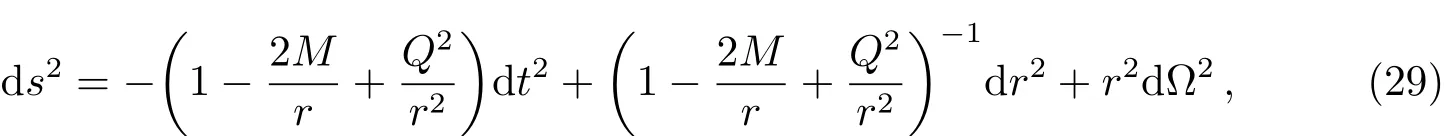
黑洞内外视界为:

黑洞外视界面积A和熵S分别为:

当Q不变时,有如下关系:

在考虑了EGUP后,可得:

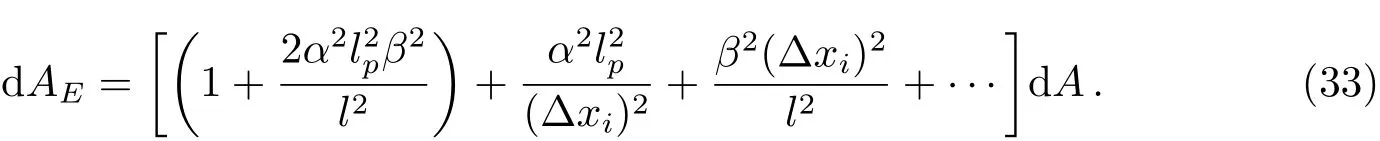
因此,对于Reissner-Nordstrom黑洞,我们取Δx=2(r+−r−),忽略高阶项,则上式可写为:

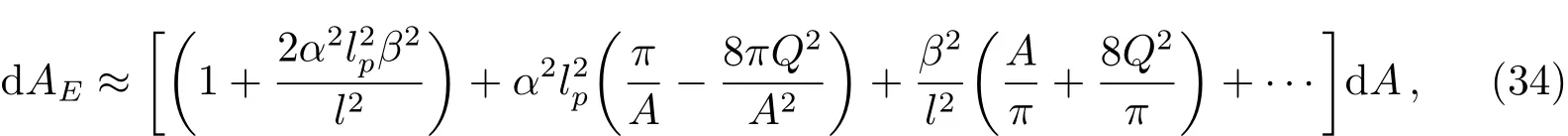
积分可得:

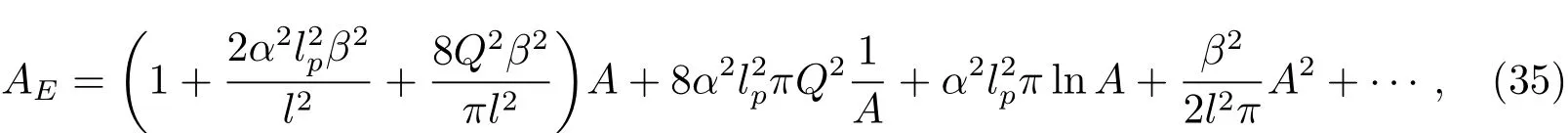
在上式的计算中应用了Q≪r+.根据Bekenstein-Hawking面积定理,即可得到考虑了EGUP后熵的表达式,即熵的修正式:

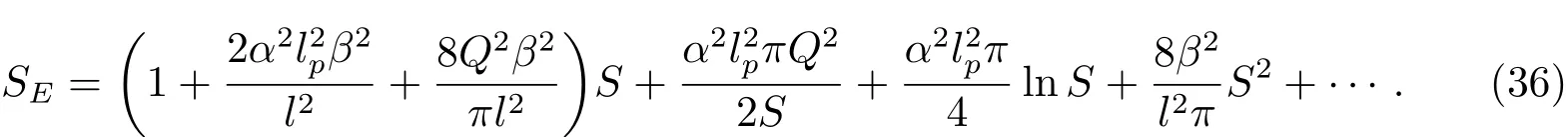
上式中S为Bekenstein-Hawking熵.

6 总结

用EGUP得到的不同黑洞熵的修正项,结果显示有1阶、2阶和对数项等,而且这些修正项的系数皆为正,且比Bekenstein-Hawking熵要小.EGUP是一个适用于大尺度的理论,与弦理论得到的很多结论是一致的,因此和GUP相比,适用范围更广.对于拥有单视界以及非极端内视界的黑洞均有效,所以可以对复杂时空的熵修正进行研究,并可以为黑洞熵对数修正项系数的确定提供参考.

[1]Bekenstein J D.PhRv,1973,7:2333

[2]Hawking S W.Nature,1974,248:30

[3]Medved A J M,Vegenas E C.PhRv,2004,70:124021

[4]Chatterjee A,Majumdar P.PhRvL,2004,92:141301

[5]Das S.CQGrv,2002,19:2355

[6]赵仁.雁北师范大学学报,2006,22:21

[7]Medved C A.PhRvD,1964,135:849

[8]Yang R J,Zhang S N.PhRvD,2009,79:124005

[9]Kim Y W,Park Y J.PhLB,2007,655:172

[10]Liu W B.ChPhL,2003,20:440

[11]Wang F J,Gui Y X,Zhang Y.GReGr,2009,41:2381

[12]杨学军,赵峥.物理学报,2011,60:060401

[13]韩亦文,洪云,杨树政.物理学报,2007,56:10

[14]贺峰,赵凡.物理学报,2009,58:740

[15]黄海,贺峰,孙航宾.物理学报,2012,61:110403

[16]刘晓莹,张甲.物理学报,2006,55:5638

[17]赵仁,李怀繁,张丽春.物理学报,2009,58:2193

[18]Park M.PhLB,2008,659:698

[19]Chang L N,Minic D,Okaruma N,et al.PhRv,2002,65:125028

[20]Kempf A.JMP,1994,35:4483

[21]Hinrichsen H,Kempf A.JMP,1996,38:1347

[22]Brett B,Marco C.GReGr,2005,37:1255

[23]Camellia G A,Majumdar P.PhRv,2004,70:107501

[24]Gar fi nkle D,Horowitz,Strominger A.PhRv,1991,43:3140

[25]Shen S,Jing J L.CQGrv,2005,22:533

Extended Generalized Uncertainty Principle and the Correction Value to the Black Hole Entropy

BAI Ji-long WEN Ting-dun
(Department of Physics,North University of China,Taiyuan 030051)

Recently,great attention has been paid to the quantum correction value of black hole’s Bekenstein-Hawking entropy,especially for the coefficient of the logarithmic correction term of the black hole entropy.On the basis of the GUP(Generalized Uncertainty Principle),we introduced the EGUP(Extended Generalized Uncertainty Principle),and calculated the correction value of three types of space-time by using the area theorem.The results showed that the coefficient of black hole entropy correction is positive.The calculation method is not only applied to the single horizon space-time, but also suitable for the double horizon space-time.The black hole entropy correction value was calculated based on the EGUP.Compared with the GUP,the EGUP can be applied in a large scale space-time,thus,its application scope is wider.The calculation method is concise,and the physical meaning is clear.It provides a reference for the determination of the coefficient of the logarithmic correction term to the black hole entropy.

black hole physics,gravitation,stars:black holes,large-scale structure of universe

P145;

A

10.15940/j.cnki.0001-5245.2015.01.001

2014-05-16收到原稿,2014-08-11收到修改稿

∗国家自然科学基金项目(60776062,50730009)资助†tdwen@nuc.edu.cn