柔性扑翼气动结构耦合特性数值研究

陈利丽，宋笔锋，宋文萍，杨文青

柔性扑翼气动结构耦合特性数值研究

陈利丽1，宋笔锋2，宋文萍2，杨文青2

(1.中国航空工业集团第一飞机设计研究院，西安710089;
2.西北工业大学翼型叶栅空气动力学国家重点实验室，西安710072)

微型扑翼体积小、重量轻，其柔性变形对气动特性有显著的影响。通过求解雷诺平均N-S方程(Reynolds－Averaged Navier-Stokes，RANS)和结构动力学方程，对微型柔性扑翼飞行器的气动结构耦合特性进行了数值模拟研究。针对微型扑翼的大幅运动，发展了适用于扑翼的气动结构耦合数值计算方法，研究了微型扑翼的气动结构耦合特性。通过求解雷诺平均Navier-Stokes(RANS)方程得到微型扑翼的非定常气动特性;利用哈密顿原理(Hamilton Principle)推导了扑翼的结构动力学方程，采用结构有限元方法对该动力学方程进行离散并求解，得到扑翼的动态结构特性;采用松耦合方法进行迭代。计算结果与风洞实验结果相比吻合良好，验证了所发展方法的有效性。在此基础上研究了惯性力和关键运动参数对柔性扑翼气动及结构特性的影响规律，有助于比较详细、全面地了解微型扑翼的气动机理，为柔性扑翼的设计提供了参考依据。

微型扑翼;气动结构耦合;雷诺平均Navier-Stokes;结构动力学;非定常气动特性

0 引言

微型扑翼研究工作者们在长期研究中发现，柔性结构变形对扑翼的气动特性有显著影响［1-7］。因此，在微型扑翼飞行器的结构设计中可以考虑根据气动方面的需要，控制柔性扑翼产生适当的结构变形来改善扑翼的气动特性。例如，在翼梢部分需要相对柔软的结构和更高的运动速度来提高推力特性;而翼根部分需要相对坚固的结构来抑制结构变形，从而保证翼型剖面维持良好的升力特性［8］。

影响扑翼柔性结构变形的因素主要有以下三方面:(1)气动载荷(扑翼自身的运动和飞行状态产生);(2)惯性载荷(扑翼自身的运动和结构重量产生);(3)结构弹性(扑翼结构刚度产生)。其中，气动载荷与结构弹性是相互耦合的，气动载荷与结构变形相互影响。因此，在对扑翼非定常气动特性进行数值模拟时，有必要考虑结构弹性的影响。惯性载荷取决于扑翼自身的运动以及结构质量分布。一旦确定以上条件，即可由结构有限元方法(Finite Element Method，FEM)求得扑翼的结构变形。

扑翼机构的运动方式主要取决于两个参数:挥舞角和扑动频率。扑翼的运动方式影响惯性载荷以及空气动力特性，进而影响扑翼的柔性结构变形。

由理论分析可知，对于做正弦规律运动的扑翼，其最大惯性载荷分别与扑动频率的平方和挥舞角呈正比关系。这说明扑翼的柔性结构变形对扑动频率的变化表现得更加“敏感”，并且增加扑动频率对机构来说更容易实现。因此，扑动频率可以用来作为控制柔性扑翼结构变形的主要参数。固定扑动频率、增大挥舞角使扑翼获得更高的瞬时扑动速度，与对惯性力的影响相比，将会带来更多的气动方面的影响。

21世纪以来，随着实验技术和计算技术的发展，国内外研究学者分别通过实验和计算两种方法对柔性扑翼气动结构耦合特性进行了一些研究。Heathcote等人［9］通过实验方法对做沉浮运动的柔性扑翼刚度对推力特性的影响进行了研究，结果表明，与刚性扑翼相比，柔性扑翼能够产生更大的推力，并通过水洞实验对半展弦比为3、做沉浮运动的NACA0012矩形机翼气动特性进行测量，发现展向柔性变形能够显著提高扑翼的推力。在数值计算方面，Wu等人［10］发展了一种多学科耦合实验方法，测量了六副不同结构(每副机翼均为板条-薄膜结构)的微型扑翼做单自由度扑动运动时的气动弹性响应和气动特性。通过数字图像关联系统测量结构变形，通过载荷传感器记录作用于扑翼上的气动载荷，利用数字粒子图像测控技术(DPIV)测量流场特性。他们的研究结果表明，结构变形对柔性扑翼气动特性有显著影响，通过适当的柔性结构变形，能够获得更好的气动特性。Singh等人［11-13］利用自行开发的实验装置和仿生扑动机构来测量机翼结构的推力特性，结果表明，在其实验状态范围内，惯性力对机翼结构变形起主导作用。由此说明，在相关气动结构耦合研究中考虑惯性力的影响是非常必要的。Zhu等［14］发展了一套基于三维边界元法和二维非线性薄钢板结构动力学模型方法的气动结构耦合分析求解器，并将数值模拟结果与Heathcote［9］做沉浮运动的柔性扑翼实验结果进行对比，验证了算法的正确性。

西北工业大学针对微型扑翼气动结构耦合特性开展了一些研究工作:杨文青等人［15］发展了基于非定常雷诺平均N-S方程和静态结构有限元方法的气动结构耦合求解器，初步研究了考虑柔性变形的微型扑翼气动特性。但是该方法没有考虑到惯性力和运动加速度的影响，而对于碳杆-薄膜结构扑翼飞行器，惯性力和运动加速度的影响是不应忽视的。

本文发展了一套适用于扑翼气动结构耦合特性的数值模拟方法:利用Hamilton原理，对动能和应变能进行变分，得到扑翼动力学方程，采用结构有限元方法对该方程进行离散并求解，得到微型扑翼的动态结构特性;通过求解三维非定常雷诺平均Navier-Stokes方程获得精确的非定常气动特性［16］;采用松耦合方法进行迭代;采用径向基函数(radial basis function，RBF)方法进行气动网格与结构网格之间的数据传递［17］。采用上述方法对柔性扑翼气动特性进行数值模拟，计算结果与风洞实验结果吻合良好，验证了该方法的有效性。在此基础上进一步对柔性扑翼的气动结构耦合特性展开详细的数值模拟研究，并对惯性载荷、气动载荷及其影响下的扑翼柔性结构变形进行定量分析，分别研究两个重要运动参数(扑动频率、挥舞角)对柔性扑翼气动结构特性的影响。

1 流动控制方程

积分形式的三维非定常可压缩雷诺平均N-S方程可写成如下形式:

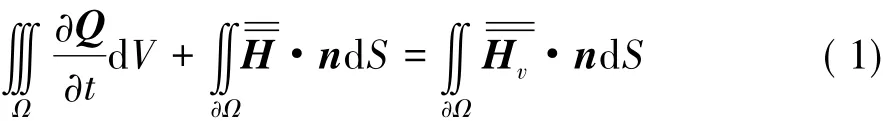
其中，

其中，q=(u，v，w)T为流体速度矢量，qb为柔性扑翼表面边界的运动速度矢量，Ix，Iy，Iz分别为直角坐标系单位坐标向量。τ和β分别为粘性应力和传热项。

采用有限体积法求解上述方程组［16，18］。时间推进采用基于LU-SGS迭代的全隐式格式，空间离散采用Jameson中心格式，湍流模型采用k-ω SST模型。绕扑翼的网格为C-O拓扑结构的结构化网格，采用基于广义无限插值理论的代数网格方法自动生成［19］，非常适合扑翼的扑动运动，完全适用于柔性扑翼的气动结构耦合计算，网格拓扑结构如图1所示。

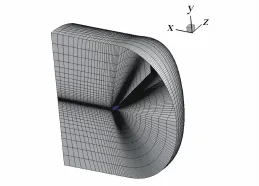
图1 扑翼C-O结构网格Fig.1Flapping wing C-O type grid

2 结构动力学方程

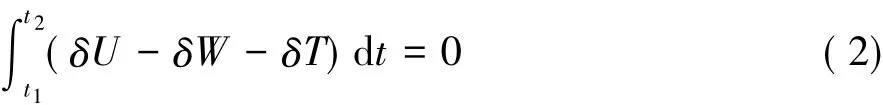
利用哈密顿原理，扑翼的结构运动方程可以表示为:其中，t1，t2表示任意时刻，δU、δW、δT分别代表应变能项、动能项和外力所做的功。

柔性扑翼结构如图2所示，由碳纤维骨架和聚醚薄膜蒙皮结构组成，考虑到聚醚薄膜蒙皮仅能承受张力，主要变形为碳纤维骨架所产生。碳纤维骨架作为主要的受力结构，其承受大部分弯矩和所有的剪力。

图2 柔性扑翼模型Fig.2Flexible flapping wing

扑翼模型的结构几何参数为:前梁2.0mm，斜梁1.5mm，翼肋1.2mm。

对碳纤维杆的材料特性进行测量，结果如图3所示。

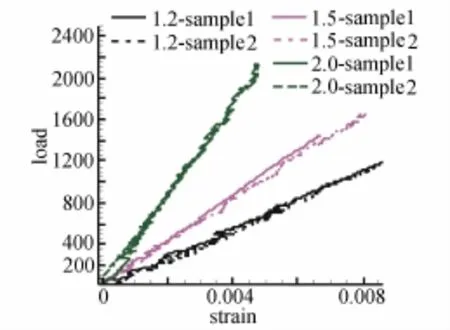
图3 碳纤维杆载荷-应变曲线Fig.3Load-strain curve of carbon fiber

由图可以看出，试验结果的重合性良好。经过对试验测量结果的整理，得到了碳纤维杆试件的弹性模量，见表1。

表1 碳纤维杆复合材料弹性模量Table 1Elastic modulus of carbon fiber

采用基于铁木辛哥梁结构理论的梁单元来模拟碳纤维杆结构。该单元模型适合于分析从细长到中等粗短的梁结构，并考虑了碳纤维杆剪切变形的影响。

首先，对应变能项进行变分。利用材料的本构关系，可以得到应变能的变分形式:

其中，［Q］为本构关系矩阵。

对动能项进行变分。图4为做俯仰挥舞运动的扑翼的参考坐标系。其中惯性坐标系Xi，Yi，Zi固连于翼根前缘位置处。挥舞角ψ表示挥舞坐标系Xf、Yf、Zf绕Xp轴旋转角度。俯仰角α为俯仰坐标系Xp、Yp、Zp绕Xp轴旋转角度。偏转角θ为梁(前梁、翼肋、斜梁)局部坐标系绕Zf轴旋转角度。坐标系之间的转换关系可以表示为如下形式:

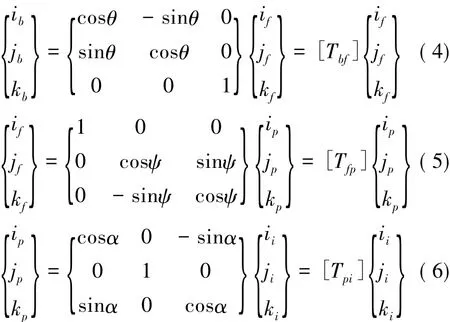
其中，运动参数α、ψ均为时间t的函数。

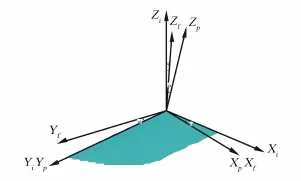
图4 扑翼坐标系Fig.4Flapping wing coordinate system

固连于梁上任一点(ξ1，0)在局部坐标系上的坐标可以表示为:

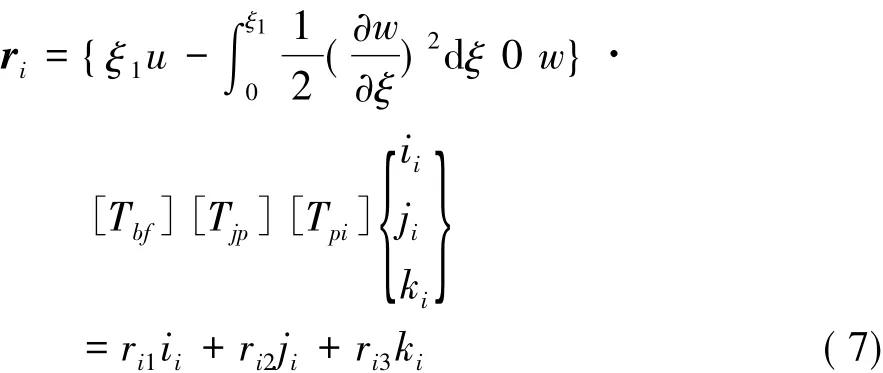
其中u、w为ξ、t的函数，分别表示轴向变形位移和挠度变形位移。

对位置坐标进行求导，可以得到任一点的速度表达式:

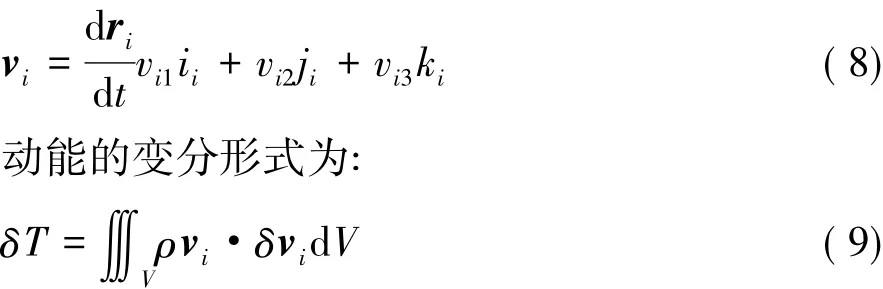
其中ρ为材料的密度。

将应变能、动能的表达式离散到结构单元内，对动能项进行变分，从中提取出质量矩阵、动态刚度矩阵和单元体积力项，分别为:

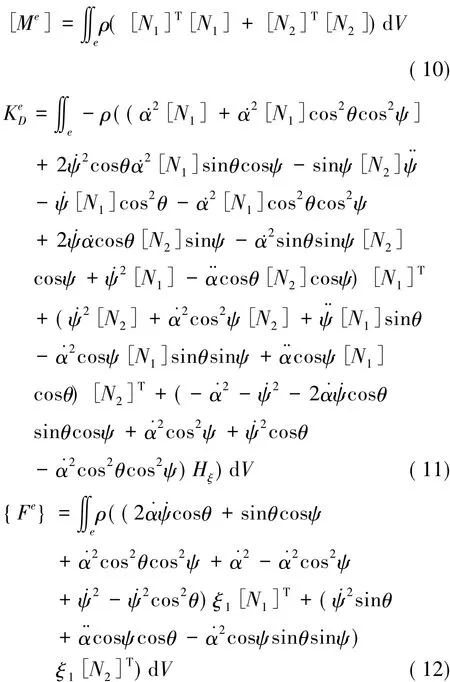
其中N1、N2分别表示u和w的形状函数。

利用单元节点之间的联系，对单元质量矩阵、静态/动态刚度矩阵和单元体积力矢量进行组装，可得到整体质量、刚度矩阵和整体体积力矢量。由此，可以得到离散形式的结构运动方程:

其中F(t)由气动力以及运动加速度产生的惯性力项组成。

对式(13)进行离散时间离散并求解［20］，可以得到t时刻的位移、速度以及加速度。

3CFD/CSD耦合方法

本文的CFD/CSD耦合采用松耦合策略，具体过程如下:

(1)通过求解非定常Navier-Stokes方程得到非定常气动力;

(2)把气动网格的气动力转换到结构网格上，对扑翼结构动力学方程进行求解得到相应时刻扑翼的结构变形位移;

(3)将结构网格的变形位移转换到气动网格上，更新柔性扑翼外形;

(4)检查结构变形是否收敛，如果收敛，则计算结束;

(5)更新结构变形后回到第1步。

采用该耦合方法，可以在3-4个周期内达到收敛。

4 算例验证与分析

对柔性扑翼模型进行了数值模拟，并将计算结果与风洞实验结果进行比较。

4.1 扑翼运动模式

扑翼机构的运动为挥舞运动，如图5所示。

图5 扑翼运动示意图Fig.5Flapping wing movement

扑翼运动规律表示如下:

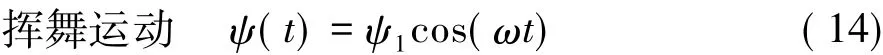
其中，ψ的取值均以上反为正，Ψ1为挥舞运动的振幅。

4.2 算法验证

4.2.1 网格和时间精度验证

首先对网格收敛性和时间精度进行了验证。分别计算了在三种不同网格密度和时间步数下的周期性升力系数，结果如图6和图7所示。

图6 不同网格密度计算结果比较Fig.6Comparison of result with different mesh sizes

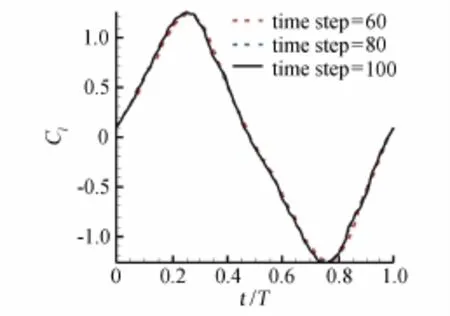
图7 不同时间步长计算结果比较Fig.7Comparison of result with different time steps

从上图可以看出，当网格密度达到152×56×56，时间迭代步数达到80步时，网格精度和时间精度均趋于收敛。

4.2.2 算例验证

将扑翼模型放入西北工业大学低湍流度风洞中进行非定常气动力的测量。风洞实验环境如图8所示。计算和实验状态为:风速8m/s，扑动频率6Hz，扑动幅度±35°。柔性机翼结构参数见表1。

在数值计算中，由于CFD计算对网格拓扑结构有限制，需要对实际柔性扑翼模型做适当简化。根据柔性翼翼肋直径，选取最大厚度为1.2%的薄翼型作为扑翼的翼剖面，如图9所示。用于CFD计算的网格单元数为152×56×56。扑翼结构计算模型如图10所示。

图10 结构计算模型Fig.10Computational structural model

计算结果与实验测量结果的比较如图11所示。

图11中，实线表示CFD/CSD耦合计算结果，虚线表示不考虑柔性结构变形的计算结果。可以看出，不考虑柔性结构变形计算出的平均升力系数随预安装角变化基本呈线性，而考虑柔性结构变形的计算结果呈现出与实验结果一致的非线性特性;平均推力系数的计算值均小于实验值，但趋势与实验值一致，且考虑柔性结构变形所得结果与实验值更为接近。对于计算结果与实验结果存在的差异，分析主要有以下原因:(1)实验中支架、洞壁等因素会对实验结果产生干扰;(2)计算模型的简化会对计算结果产生一定影响。从结果可以看出，对于研究的柔性扑翼模型，结构变形对气动特性有很大影响，因此在数值模拟中考虑柔性结构变形是十分必要的。

4.3 扑动频率对扑翼气动结构耦合特性的影响

本节研究了扑动频率对柔性扑翼气动及结构特性的影响，计算扑动频率从3Hz～12Hz范围内的变化情况，每隔3Hz计算一个结果。其余参数保持不变，分别为:风速=6m/s，挥舞角ψ1=35°，预安装角α0= 0°。扑翼的周期结构变形计算结果如图12所示。

翼梢前缘位置处柔性变形位移的大小反映了柔性扑翼结构的弯曲刚度特性，但是从结构变形位移云图上不能对柔性结构变形与气动特性之间的关系进行进一步直观定量的分析。为此，根据扑翼柔性结构变形的特点，将柔性变形分解为两部分:弯曲变形(沿展向)和扭转变形(沿弦向)，分别用翼梢前缘弯曲角度αbend和翼梢后缘扭转角度αtwist表示。柔性扑翼产生的αbend和αtwist分别随扑动挥舞角的变化形成一个闭合的相位环，变化过程如图13所示。

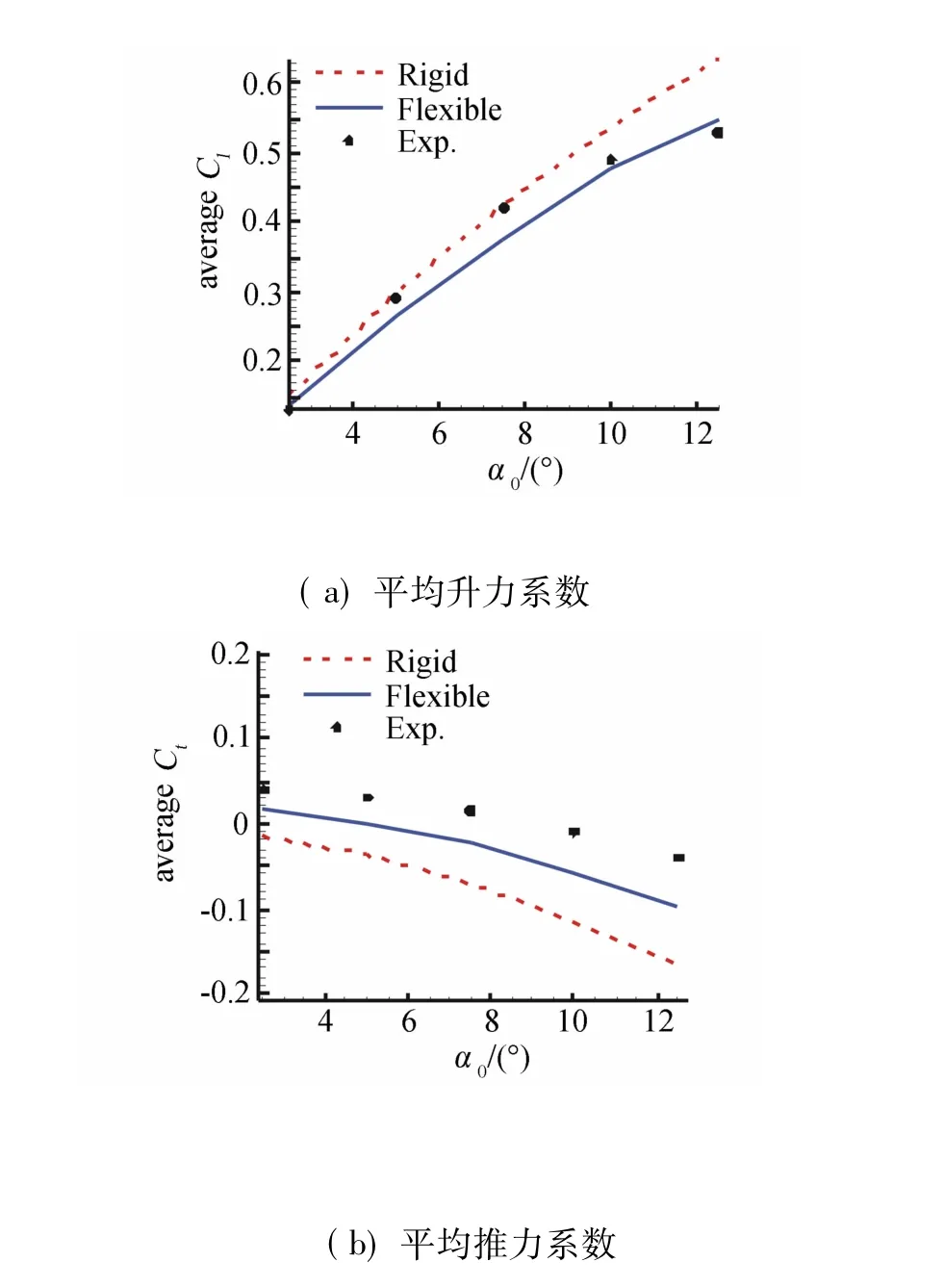
图11 计算结果与实验值比较Fig.11Comparison between computational and experimental result

图12 扑翼在3Hz、9Hz、12Hz的周期结构变形Fig.12Periodic structural deformation in 3Hz、9Hz、12Hz

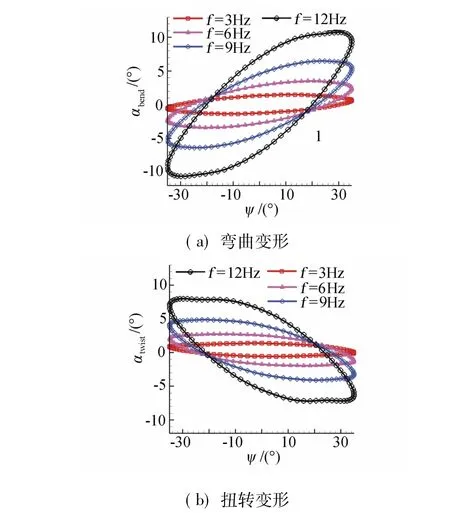
图13 扑翼在不同频率下的周期结构变形相位图Fig.13Periodic deformation phase in different frequencies

从图12和图13可以看出，柔性扑翼在扑动过程中均会产生柔性弯曲变形和扭转变形。在扑动频率为3Hz时，当扑翼从最高点往下扑时，在最高点处，扑翼产生了上翘的柔性弯曲变形;从最高点扑动到平衡位置过程中，扑翼的弯曲变形幅度逐渐增大，在平衡位置附近，扑翼变形达到最大;从平衡位置扑动到最低点过程中，扑翼上翘变形逐渐反弹，在最低位置附近，扑翼变形达到最小;从最低点上扑到平衡位置过程中，扑翼产生向下的弯曲变形，变形量先增大后减小，在7/8T时刻达到最小，从7/8T时刻扑动到最高点过程中，扑翼产生上翘的变形。

扑动频率增大到9Hz时，扑翼一周期各时刻柔性变形的趋势与3Hz时大致相同，主要区别有两点: (1)弯曲变形的幅度显著增大;(2)扑翼最大弯曲变形和最大扭转变形发生时刻提前，更靠近下扑和上扑初始位置。

扑动频率继续增大到12Hz时，扑翼的变形幅度持续增大，最大弯曲变形和最大扭转变形发生在下扑和上扑的初始时刻。

进一步研究扑翼气动特性随扑动频率的变化趋势以及柔性结构变形对扑翼气动特性的影响。周期性升力系数和推力系数变化曲线如图14所示。

图14 不同频率下周期性升力系数和推力系数的变化曲线Fig.14Periodic lift and thrust coefficient in different frequencies

从图14中可以观察到，对于刚性扑翼，随着扑动频率的增加，升力系数和推力系数曲线峰值均显著增加，并且增加幅度越来越大。对于柔性扑翼，在扑动频率较低(低于6Hz)时，与刚性扑翼相比，柔性扑翼周期性升力系数曲线峰值有所降低;当扑动频率较高(高于9Hz)时，与刚性扑翼相比，柔性扑翼周期性升力系数曲线峰值有所增长，并且随着扑动频率的增大，增长幅度越来越大。

平均升力系数和平均推力系数随扑动频率的变化如图15所示。

可以观察到，对于刚性扑翼，平均升力系数随扑动频率的增加而增大，平均推力系数随扑动频率的增加略微有所增大;对于柔性扑翼，平均升力系数与刚性扑翼相比有所降低，并且随扑动频率的增加呈减小趋势，平均推力系数与刚性扑翼相比有显著增大，频率越大，增大趋势越明显。

由以上结果分析可知，由于结构变形的影响，柔性扑翼气动特性随扑动频率变化的趋势与刚性扑动情况是不同的，并且随着扑动频率的增大，柔性变形对气动特性的影响变得越来越显著。采用柔性结构能够显著提高推力特性，但对升力特性则会产生稍许不利影响;增大扑动频率有利于柔性扑翼推力特性的产生，但对柔性扑翼升力特性则有不利影响。

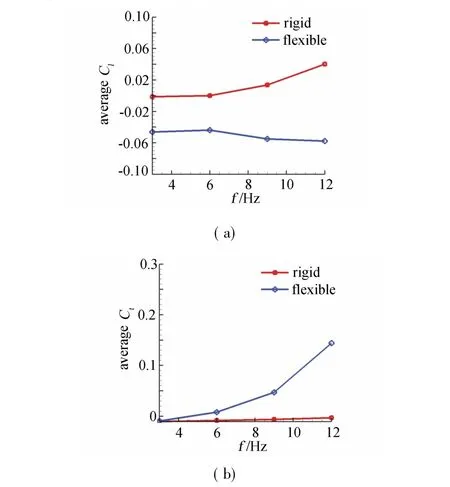
图15 平均升力系数和推力系数随着扑动频率的变化曲线Fig.15Variation of average lift and thrust coefficient with frequencies

4.4 挥舞角对扑翼气动结构耦合特性的影响

本节研究挥舞角对柔性扑翼气动及结构特性的影响，计算了挥舞角从15°～35°范围内变化的情况，每隔5°计算一个结果。其余参数保持相同，分别为:风速=6m/s，扑动频率=6Hz，预安装角α0=0°。

图16为扑翼在挥舞角为15°、25°和35°时的周期结构变形。柔性扑翼产生的αbend和αtwist随扑动过程中挥舞角变化过程如图17所示。

从图16和图17中可以看出，与随扑动频率变化趋势有所不同，柔性扑翼的弯曲变形和扭转变形幅度随挥舞角的增大呈线性增长，而最大弯曲变形和最大扭转变形发生时刻则基本不发生变化。由此可知，挥舞角变化只改变结构变形的峰值，不改变柔性变形的相位。

为研究扑翼气动特性随挥舞角的变化趋势，分别计算了不同挥舞角下刚性和柔性扑翼的气动特性。周期性升力系数和推力系数变化曲线如图18所示。

从图18中可以看到，对于刚性扑翼，随着挥舞角的增加，升力系数和推力系数曲线峰值均有所增加。柔性扑翼升力系数曲线峰值与刚性扑翼相比略微有所降低，但推力系数曲线峰值则有明显升高，并且随着挥舞角的增大，升高幅度越来越大。

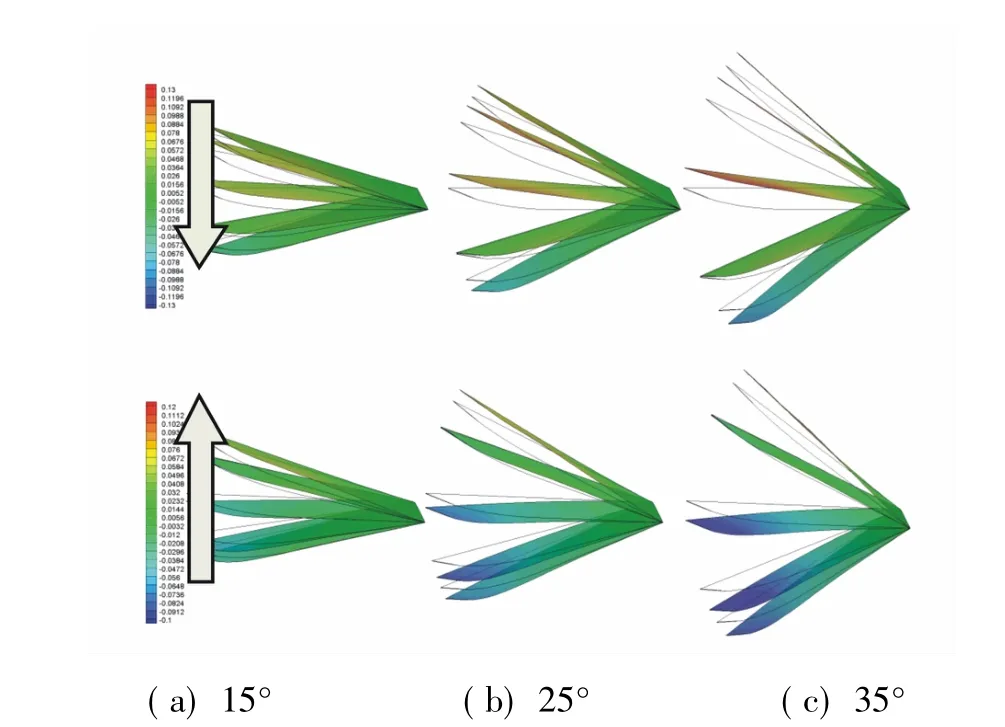
图16扑翼在15°、25°、35°的周期结构变形Fig.16Periodic structural deformation in15°、25°、35°

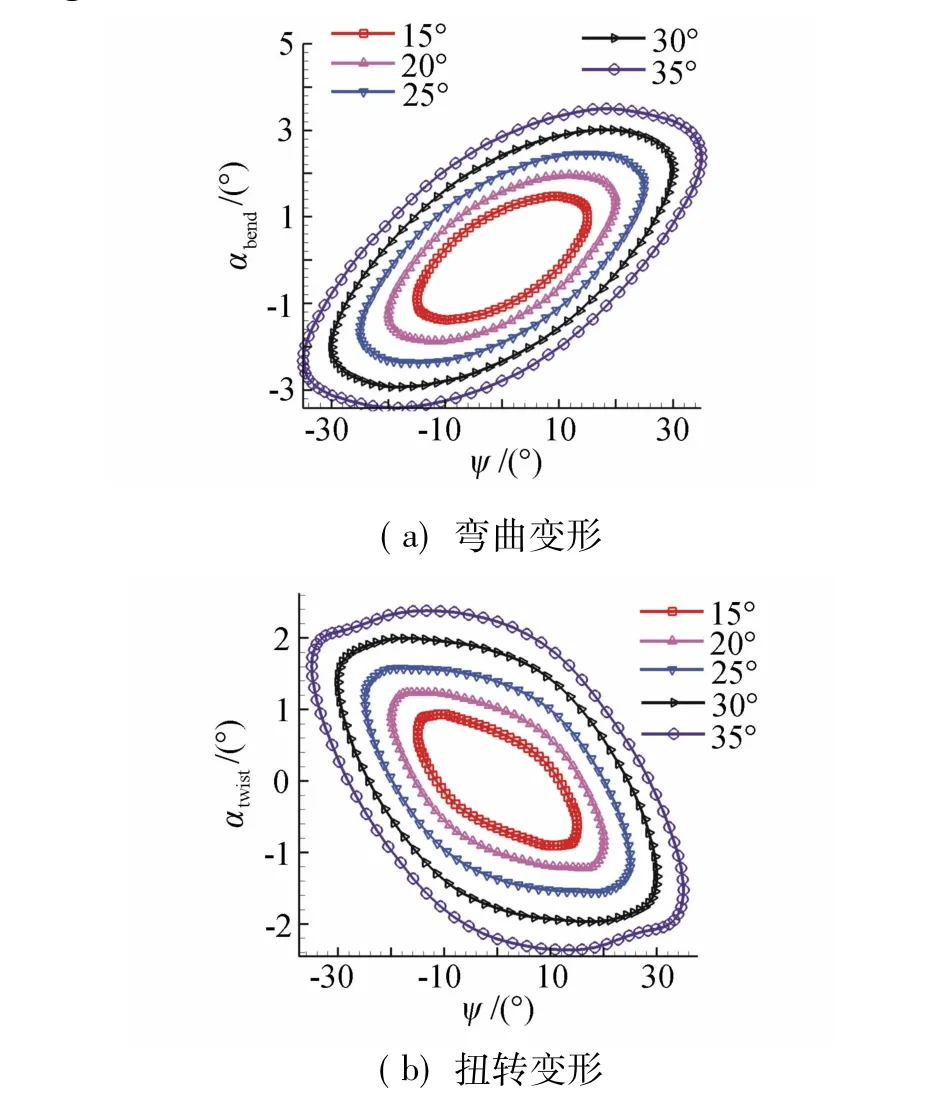
图17 扑翼在不同挥舞角下的周期结构变形相位图Fig.17Periodic deformation phase in different flapping angles

平均升力系数和平均推力系数随挥舞角的变化如图19所示。

由图19中可以观察到，对于刚性扑翼，随着挥舞角的增加，平均升力系数基本保持不变，平均推力系数有略微增长的趋势;对于柔性扑翼，平均升力系数随挥舞角的增加基本不发生变化，但与刚性扑翼相比有所降低，平均推力系数与刚性扑翼相比显著增大，随挥舞角的增加一直增大。

由此可知，增大挥舞角有利于柔性扑翼推力特性的产生，对柔性扑翼升力特性则几乎不产生影响。

图18 不同挥舞角下周期性升力系数和推力系数的变化曲线Fig.18Periodic lift and thrust coefficient in different flapping angles

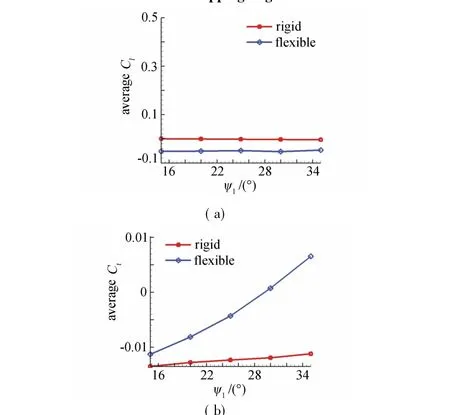
图19 平均升力系数和推力系数随着挥舞角的变化曲线Fig.19Variation of average lift and thrust coefficient with flapping angle

5 结论

本文从结构变形、气动特性两个方面研究了两个关键运动参数(扑动频率、挥舞角)对柔性扑翼气动结构耦合特性的影响、结构变形对柔性扑翼气动特性的影响以及柔性扑翼随运动参数的变化趋势，得到了柔性扑翼气动特性方面的一些基本规律，研究结果在各节中均有小结。从研究结果可以得出，柔性扑翼产生的结构变形对气动特性有显著影响，对柔性扑翼气动特性进行数值模拟时，考虑结构变形的影响是非常必要的。与挥舞角相比，扑动频率对柔性扑翼的气动结构特性影响表现的更为明显。

在气动特性方面，柔性扑翼结构对推力特性有显著地提升作用，并且随着扑动频率和挥舞角的增大这种作用越来越明显，而对升力特性却有不利的影响。

［1］Zeng R，Ang H S，Mei Y，et al.Flexibility of flapping wing and its effect on aerodynamic characteristic［J］.Chinese Journal of Computational Mechanics，2005，22(6):750-754.(in Chinese)曾锐，昂海松，梅源，等.扑翼柔性及其对气动特性的影响［J］.计算力学学报，2005，22(6):750-754.

［2］Unger R，Haupt M C，Horst P.Structural design and aeroelastic analysis of an oscillating airfoil for flapping wing propulsion［C］//In 46th AIAA Aerospace Sciences Meeting and Exhibit，Reno，Nevada，January 2008.AIAA 2008-306.

［3］Liani E，Guo S，Allegri G.Aerodynamics and aeroelasticity of flexible flapping wings［R］.2007.

［4］Kim D K，Lee J S，Lee J Y，et al.An aeroelastic analysis of a flexible flapping wing using modified strip theory［J］.Active and Passive Smart Structures and Integrated Systems，2008，6928:1-8.

［5］Hamamoto M，Ohta Y，Hara K，et al.Application of fluid-structure in-teraction analysis to flapping flight of insects with deformable wings［J］.Advanced Robotics，2007，21(1-2):1-21.

［6］Liani E，Guo S，Allegri G.Aeroelastic effect on flapping wing perfor-mance［C］//In 48th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference，Honololu，Hawaii，April 2007.AIAA 2007-2412.

［7］Ennos A R.The importance of torsion in the design of inset wings［J］.Journal of Experimental Biology，1988，140:137-160.

［8］Pin Wu.Experimental characterization，design，analysis and optimization of flexible flapping wings for micro air vehicles［D］.［PhD Dissertation］.University of Florida，2010.

［9］Heathcote S，Wang Z，Gursul I.Effect of spanwise flexibility on flapping wing propulsion［J］.Journal of Fluids and Structures，2008，24(2):183-199.

［10］Wu P，Ifju P，Stanford B，et al.A multidisciplinary experimental study of flapping wing aeroelasticity in thrust production［C］//In 50th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference，Palm Springs，CA，May 2009.AIAA 2009-2413.

［11］Singh B.Dynamics and aeroelasticity of hover capable flapping wings:experiments and analysis［D］.［PhD Dissertation］.Department of Aerospace Engineering，University of Maryland，College Park，Maryland，2006.

［12］Singh B，Chopra I.Insect-based flapping wings for micro hovering air ve-hicles:experimental investigationsp［C］//American Helicopter Society International Specialists Meeting on Unmanned Rotorcraft，Arizona，January 2004.

［13］Singh B，Chopra I.Dynamics of insect-based flapping wings:loads and validation［C］//In 47t/AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference，Newport，Rhode Island，May 2006.AIAA 2006-1663.

［14］Zhu Q.Numerical simulation of a flapping foil with chordwise or spanwise flexibility［J］.AIAA Journal，2007，45(10):2448-2457.

［15］Yang W Q，Song B F，Song W P.Fluid-structure coupling research for micro flapping-wing［C］//the 27th International Congress of Aeronautic Sciences，Nice，France.Sep，19-24，2010.

［16］Xie H，Song W P，Song B F.Numerical solution of navier-stokes equations for flow over a flapping wing［J］.Journal of Northwestern Polytechnical University，2008，26(1):104-109.(in Chinese)谢辉，宋文萍，宋笔锋.微型扑翼绕流的N-S方程数值模拟［J］.西北工业大学学报，2008，26(1):104-109.

［17］Bechert A，Wendland H.Multivariate interpolation for fluid-structure-interaction problems using radial basis functions［J］.Aerospace Science and Technology，2001，5(2):125-134.

［18］Song W P，Yang Y，Qiao Z D，et al.Unsteady N-S calculations using a dual-time stepping method for airfoils oscillating at high angle of attack［J］.Acta Aerodynamica Sinica，1999，17(4):466-471.(in Chinese)宋文萍，杨永，乔志德，等.双时间法求解大迎角翼型绕流非定常N-S方程［J］.空气动力学学报，1999，17(4):466-471.

［19］Xie H，Song W P，Song B F.Airfoil design of a micro-flapping wing based on CFD［J］.Journal of Northwestern Polytechnical University，2008，27(2):227-233.(in Chinese)谢辉，宋文萍，宋笔锋.基于CFD方法对微型扑翼翼型设计的研究［J］.西北工业大学学报，2008，27(2):227-233.

［20］Zhu B，Qiao Z D，Gao C.Numerical simulation of transonic flutter for airfoil using approximate boundary conditions［J］.Journal of Northwestern Polytechnical University，2008，26(2):254-258.(in Chinese)朱标，乔志德，高超.基于近似边界条件的翼型跨声速颤振数值模拟研究［J］.西北工业大学学报，2008，26(2):254-258.

Numerical aerodynamic-structural coupling research for flexible flapping wing

Chen Lili1，Song Bifeng2，Song Wenping2，Yang Wenqing2
(1.The AVIC First Aircraft Institute，Xi'an710089 China; 2.National Key Laboratory of Science and Technology on Aerodynamic Design and Research，School of Aeronautics，Northwestern Polytechnical University，Xi'an710072，China)

Due to the small size and light weight，flexible deformation plays an important part in flapping wing aerodynamics.the aero-elastic performances of Flapping-wing Micro Air Vehicle(FMAV) are researched by solving the Reynolds-Averaged Navier-Stokes(RANS)equations and structural dynamic equations.An aerodynamic-structural coupling computational framework is developed，which is able to simulate aerodynamic-structural coupling characteristics of flexible flapping wings.The flapping wing's unsteady aerodynamic characteristics is obtained by solving Reynolds Average Navier-Stokes(RANS)equations.Structural dynamic equations capable of describing the flapping wing's movement are derived by using Hamilton principle，then discreted through finite element method and solved by Newmark solution to get structural characteristics.Loose coupling method is used.On the basis of the above work，CFD/ CSD(Computational Fluid Dynamics/Computational Structural Dynamics)grid data exchange method，dynamic grid technology as well as coupling method are further investigated，and finally a complete set of CFD/CSD coupling solver is developed.Computational results show good agreement with experimental results，which prove that the method developed in this paper are valid and suit for simulation of flexible flapping wing.Effect of inertia loads and kinetic parameters arealso investigated，which can help to understand the mechanisms of flexible flapping wing's aeroelasticity and give a guidance in the design of flexible flapping wing.

micro flapping wing;aerodynamic-structural coupling;Reynolds-averaged Navier-Stokes;structural dynamics;unsteady aerodynamic characteristics

V211.3

Adoi:10.7638/kqdlxxb-2012.0210

0258-1825(2015)01-0125-08

2012-12-19;

2014-12-23

中国博士后科学基金(20100481369)

陈利丽(1985-)，女，安徽合肥人，博士研究生，主要从事微型飞行器方向研究.E-mail:lilichen@mail.nwpu.edu.cn

陈利丽，宋笔锋，宋文萍，等.柔性扑翼气动结构耦合特性数值研究［J］.空气动力学学报，2015，33(1):125-133.

10.7638/kqdlxxb-2012.0210.Chen L L，Song B F，Song W P，et al.Numericalaerodynamic-structural coupling research for flexible flapping wing［J］.Acta Aerodynamica Sinica，2015，33(1):125-133.