基于岩石物理的致密碎屑岩气藏岩性及流体概率预测

洪 忠,张猛刚,朱筱敏

(1.中国石油天然气股份有限公司勘探开发研究院西北分院,甘肃兰州730020;2.中国石油大学(北京)地球科学学院,北京102249)

基于岩石物理的致密碎屑岩气藏岩性及流体概率预测

洪 忠1,张猛刚1,朱筱敏2

(1.中国石油天然气股份有限公司勘探开发研究院西北分院,甘肃兰州730020;2.中国石油大学(北京)地球科学学院,北京102249)

我国致密碎屑岩气藏具有低孔、低渗、储层非均质性强等特点。由于致密气藏埋深较大,目的层地震资料通常信噪比低、主频低,利用单一叠前弹性参数预测有效气层的精度有限。为提高致密气藏的预测精度,以建立适用于低孔、低渗气藏的岩石物理模型为基础,优选出对气层识别敏感的弹性参数组合。通过确定性岩石物理模型和统计岩石物理方法实现测井资料中没有的储层及泥岩的岩石物理表征,并和原测井数据结合建立各类岩性概率密度函数。最终基于地震弹性参数反演数据和概率密度函数,利用贝叶斯岩性判别方法预测岩性流体概率。结果表明:Xu-White模型适用于表征工区低孔、低渗砂岩。运用多弹性参数贝叶斯判别方法能提升岩性识别的成功率。多变量Monte Carlo随机模拟方法有效地拓展了泥岩的岩石物理表征。岩性及流体概率预测结果与实际钻井结果一致,证明了该套方法预测致密碎屑岩气藏的有效性。

Xu-White模型;多变量Monte Carlo随机模拟;贝叶斯岩性判别;致密碎屑岩气藏

致密碎屑岩气藏通常埋深较大,具有低孔隙度、低渗透率、孔隙结构复杂、流体非均匀饱和等特点。储层含气后纵波阻抗降低,和围岩的差异小,甚至两者的纵波阻抗值域重合,难以应用叠后地震资料来有效预测气层。引入包含横波信息的叠前地震资料虽然提高了识别气藏的能力,但单一叠前弹性参数有效识别各类岩性的精度还是有限。自Mukerji等[1]和Avseth等[2]首先尝试应用统计岩石物理方法并结合叠前弹性参数开展定量储层预测研究以来,基于岩石物理和贝叶斯框架,充分利用多弹性参数联合信息的地震储层预测方法已广泛应用于定量地震储层解释中。Mukerji等[3]综合应用马尔科夫-贝叶斯统计、贝叶斯岩性判别和叠前弹性反演及随机模拟方法,定量刻画了北海浊积岩体系储层岩性及流体的平面分布。Avseth等[4-6]根据AVO属性的截距和梯度特征,利用贝叶斯判别分类方法成功划分了北海浊积岩岩性及流体类型。Bachrach[7]联合随机岩石物理模拟及基于贝叶斯框架的地震储层预测方法预测了储层的孔隙度和饱和度。Spikes等[8]基于岩石物理模型提出了应用概率地震反演方法来预测岩性和流体。González等[9]以岩石物理为约束条件,结合多点统计技术提出了一套新的地震岩性反演方法。Bosch等[10]系统总结了统计岩石物理和地质统计方法在定量地震储层预测中的作用。Grana等[11-15]综合地震反演、岩石物理及地质统计学方法,开展了一系列测井岩性及流体解释和定量地震储层参数概率预测的研究。国内学者近几年来在定量地震储层预测领域的研究也取得了长足的进步。邓继新等[16]率先利用统计岩石物理方法联合预测储层饱和度和孔隙度。郭伟等[17]利用贝叶斯统计分类技术对浊积岩储层进行了岩性及流体判别。毛宁波等[18]利用贝叶斯判别方法进行流体识别,优选出对流体敏感的属性及属性组合。晏信飞等[19]应用贝叶斯岩性判别技术对川中地区致密砂岩储层岩性及流体进行了检测。胡华锋等[20]基于贝叶斯反演框架,综合应用统计岩石物理模型及蒙特卡洛随机模拟技术实现了多种储层物性参数的联合反演。

根据致密碎屑岩气藏的地球物理响应特点,本文以鄂尔多斯盆地西南部二叠系山西组山一段含气储层为研究对象,以建立研究区的岩石物理模型为基础,将确定性岩石物理模型和统计岩石物理模型相结合,利用贝叶斯判别方法预测致密砂岩气藏的岩性及流体概率。

1 工区概况及测井数据校正

1.1 工区概况

鄂尔多斯盆地西南部上古生界主力储层位于二叠系山西组山一段及下石河子组盒八段,其中山一段有效储层为典型的低孔、低渗致密含气砂岩。山一段储层发育三角洲平原、三角洲前缘砂泥岩薄互层砂体,有效储层厚度多小于10m。其岩性以石英砂岩、岩屑石英砂岩为主。储层孔隙类型以岩屑溶孔、粒间溶孔为主,其次为晶间孔,原生孔隙不发育(图1)。储层平均孔隙度为5.58%,平均渗透率为0.17×10-3μm2[21]。根据工区山一段沉积发育及储层类型特点,将岩性划分为干砂岩、气砂岩及泥质岩3类。

1.2 测井数据特点

研究目的层山一段(S1),测井资料有W1井、W2井和W3井。各井山一段均钻遇具工业价值的气层。3口井测井曲线都包括纵波速度、横波速度、密度、自然伽马、中子孔隙度、深侧向电阻率、浅侧向电阻率曲线及针对储层段进行测井解释的孔隙度及含水饱和度资料。工区测井曲线存在以下问题:①泥岩段扩径现象严重,获得的测井资料虽然在泥岩扩径段对密度和声波曲线进行了校正,但过于简单的扩径校正方法使纵波速度和密度呈明显的线性关系(图2a),这样的异常线性关系不适合作为岩石物理建模的基础资料;②相当一部分的砂岩储层由岩屑石英砂岩构成,因此，储层段也存在扩径现象,严重影响了实测横波的质量。以W2井为例(图2b),该井山一段储层在岩性很稳定的情况下,由于扩径的影响,横波速度出现大的尖峰跳跃,显然这种现象不合理。综合以上两种情况,为满足后续岩石物理建模工作的要求,需要对各井目的层扩径段曲线进行测井环境校正。

图1 鄂尔多斯盆地西南部山一段储层孔隙类型特征

1.3 测井数据校正

采用回归分析方法对扩径段测井曲线进行环境校正。基本思路是:在目的层非扩径段,分别针对砂岩和泥岩,建立待校正曲线和受扩径影响小、稳定测井曲线间的回归关系;然后,将建立的回归关系推广到扩径段,由稳定曲线反推待校正曲线来达到曲线环境校正的目的。研究区深侧向电阻率曲线受扩径影响小,可作为首选校正参考曲线。利用上述方法分别对W1井、W2井、W3井砂岩扩径段、泥岩扩径段的纵、横波速度及密度进行校正。对于砂岩扩径段横波速度的校正,由于其在非扩径段纵、横波间的拟合系数低,采用Xu-White岩石物理模型,通过输入储层段的泥质含量、总孔隙度及含水饱和度来正演横波速度。以W1井、W2井校正结果为例(图3),从W1井、W2井的纵横波速度比与纵波阻抗交会图上可以看到,W1井校正前数据线状分布的现象得到根本改善;同时,W2井储层段纵横波速度比不合理的值域分布也校正到正常范围。

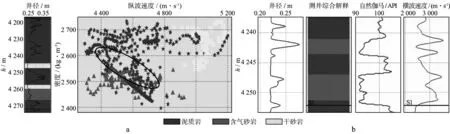
图2 W1井(a)和W2井(b)山一段测井曲线特征

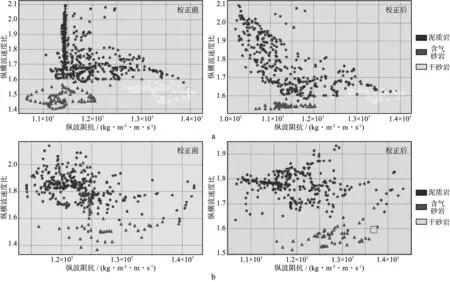
图3 W1井(a)和W2井(b)山一段测井曲线环境校正前、后交会结果

2 岩石物理建模

2.1 Xu-White岩石物理建模

研究区砂岩储层具有低孔、低渗特点。因此,需要同时考虑工区不同岩性的孔隙特点及泥质含量等因素,有针对性地选取岩石物理模型进行建模。Kuster等[22]提出适用于低孔岩石的包含体模型。Xu等[23-24]将Gassmann方程、Kuster-Toksöz模型及差分等效介质理论结合起来,提出了利用泥质含量、孔隙度大小及扁率来估算泥质砂岩纵、横波速度的方法。本文尝试选取Xu-White泥质砂岩模型对工区低孔砂岩储层进行建模。

Xu-White模型计算饱和孔隙的速度有高频和低频两种模式[25]。在高频模式下,夹杂体的体积模量被设置为流体模量,即直接应用Kuster-Toksöz模型计算出高频饱和流体速度。在低频模式下,夹杂体的体积模量被设置为0,先应用Kuster-Toksöz模型计算干岩石的弹性模量,然后通过Gassmann方程进行流体置换计算饱和流体岩石的弹性参数。本文以建立研究区温压模型为基础,将储层段测井解释的泥质含量、总孔隙度及含水饱和度数据作为基本输入参数。采用低频模式下的Xu-White模型开展岩石物理建模工作,主要步骤如下。

1) 计算岩石基质等效弹性模量。

Xu-White模型首先利用Wyllie公式计算基质混合后的纵、横波时差,然后计算基质的弹性模量。总孔隙大小由石英粒间孔隙和黏土束缚孔隙组成。同时,石英和黏土含量及总孔隙的和为1,即:

(1)

(2)

式中:φ,φs,φc分别为总孔隙度、石英粒间孔隙及黏土束缚孔隙;Vs,Vc分别为石英和黏土含量。

运用Wyllie公式计算基质混合后的纵、横波时差及密度,有:

(3)

(4)

(5)

(6)

(7)

(8)

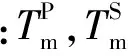
2) 计算饱和流体的体积模量。

Xu-White模型利用Wood方程计算饱和流体的体积模量Kfl及密度ρfl。

(9)

(10)

式中:Kw,Kg,ρw,ρg分别为水和天然气的体积模量及密度;Sw为含水饱和度。

3) 计算干岩石弹性模量。

Xu-White模型采用Kuster-Toksöz模型计算干岩石弹性模量。Kuster-Toksöz模型本质上是包含体模型,假设的前提之一是包含体分布太稀疏以至于不相互影响或重叠,因此Kuster-Toksöz孔隙度适用于低孔隙度岩石[22]。除了考虑包含体的弹性性质,Kuster-Toksöz模型同时还考虑了体积百分比和形状对岩石弹性特征的影响。

(11)

(12)

式中:Kd,μd分别为干岩的体积模量和剪切模量;αs,αc,φs分别为石英、黏土孔隙纵横比及石英粒间孔隙度;f(αs,αc,φs)和g(αs,αc,φs)为石英、黏土孔隙纵横比及石英粒间孔隙度的函数。因为Kuster-Toksöz模型只在孔隙度很小时适用,因此引入微分等效介质理论来克服这一限制,通过向背景材料中逐渐加入包含物来模拟双相混合物,具体方法见文献[23]和[24]。

4) 饱和流体岩石的流体替换。

采用Gassmann方程进行流体替换,计算饱和流体岩石的弹性模量,进而计算其密度(ρ)及纵、横波速度(vP,vS)。

ρ=φρfl+(1-φ)ρm

(13)

(14)

(15)

5) 岩石物理参数调节。

应用Xu-White模型可同时正演出纵、横波速度及密度。通常纵波速度及密度测井资料是具备的。因此,比较预测曲线与实测曲线,通过调节输入参数的大小,反复迭代,使预测曲线与实测曲线实现最佳匹配,从而提高横波速度预测的精度。实际上,该方法是在一定约束条件下反演横波速度,相关学者也开展了此类方法的研究[26-32]。实测纵波速度的质量相对较好,因而被作为最佳约束目标函数。在调节输入参数方面,张元中等[30]运用实际地层和饱和水纵波速度之间函数关系式,通过调节函数关系式中的参数来使实测和预测纵波速度间的差异最小,进而保证横波速度预测的精度;林凯等[31]通过在干岩泊松比和基质体模量的各自范围内反复取值,使实测和预测纵波速度间的差异在允许误差范围内,从而提高纵、横波速度预测的精度。砂泥岩扁率为干岩模量的函数,本文通过调节石英和黏土的扁率,实现干岩模量的最优化估算,最终完成Xu-White模型的高质量建模。

2.2 Xu-White模型建模效果及原因分析

以W1井为例(图4),可以看到，在储层段中,Xu-White模型正演的纵波速度和纵波曲线拟合程度最高,横波速度次之,密度在干砂岩段误差稍大,但总的来说弹性参数的正演曲线和原始曲线匹配程度较好。

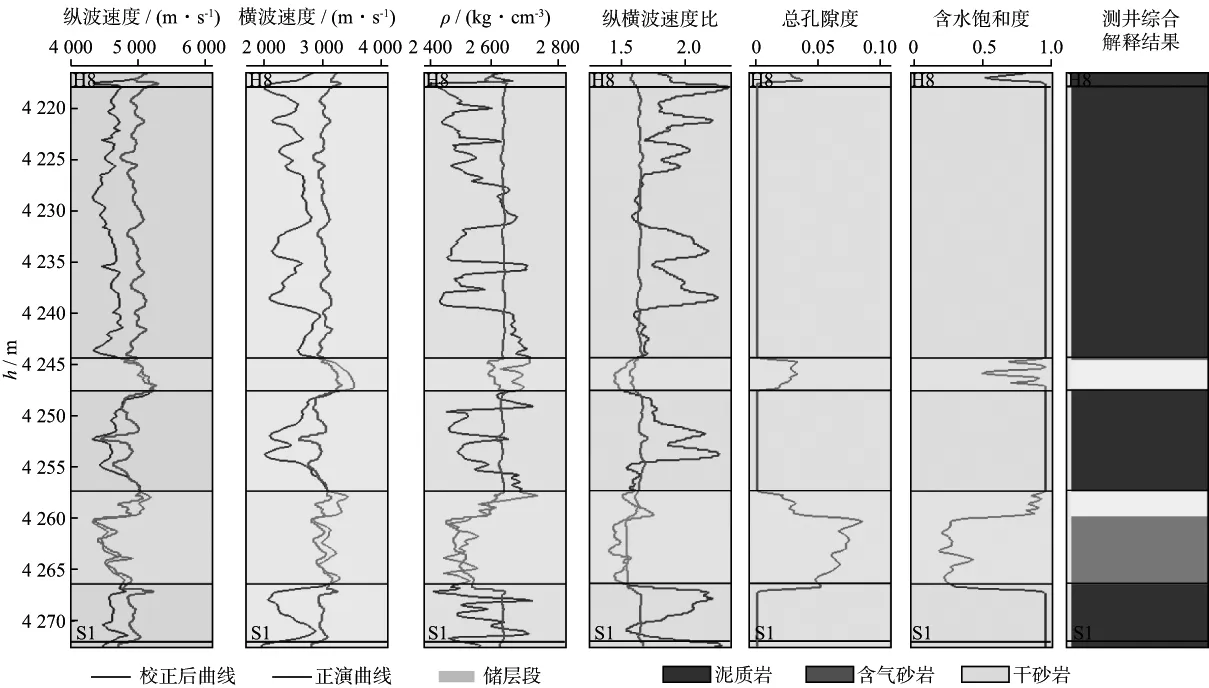
图4 W1井山一段Xu-White模型岩石物理建模

设计包含不同泥质含量、不同孔隙度、不同饱和度的虚拟井来模拟合理范围内所有可能的测井储层参数。石英和黏土的扁率则为运用Xu-White模型正演W1井时对应最优化的扁率值。通过输入以上模拟储层参数及最优化石英和黏土扁率,应用低频模式下的Xu-white模型来建立弹性参数交会解释模板(图5)。

从图5可看到,W1井、W2井和W3井山一段含气砂岩及干砂岩纵波阻抗和纵横波速度比的交会分布特征和Xu-White模型岩石物理解释模板匹配程度较高。然而,同时可以看到泥岩段的点多在Xu-White模型范围之外。

以上现象表明,Xu-White模型适用于表征研究区低孔、低渗透砂岩,但不适用于表征研究区的泥岩段弹性参数。工区砂岩储层具有低孔、低渗特点,其目的层薄片(图1)反映了微裂隙的存在。微裂隙在流体充填后会对岩石速度产生明显影响。砂岩含气后纵横波速度比显著变小(图5),表明受微裂缝的影响,含气砂岩纵波速度会明显变小。这一认识可以通过微分等效模量模型等双孔隙介质模型来解释。微裂隙的纵横比在模型中设为0.01,将该纵横比作为输入,计算出的饱和流体岩石的速度会发生很大变化。因此,这也是对致密砂岩能够进行流体检测的岩石物理基础。实测纯泥岩的弹性参数与Xu-White模型匹配较差(图5),可能是由于岩石物理量版的建立涉及到Gassmann方程的计算。Gassmann方程适用的假设条件包括:①岩石(基质和骨架)宏观上是均匀各向同性的;②所有孔隙都是连通的;③孔隙中充满流体。Gassmann方程只适合砂岩地层,没有考虑岩性变化带来的影响。因此,实测泥岩段的点多在Xu-White模型量版范围之外。

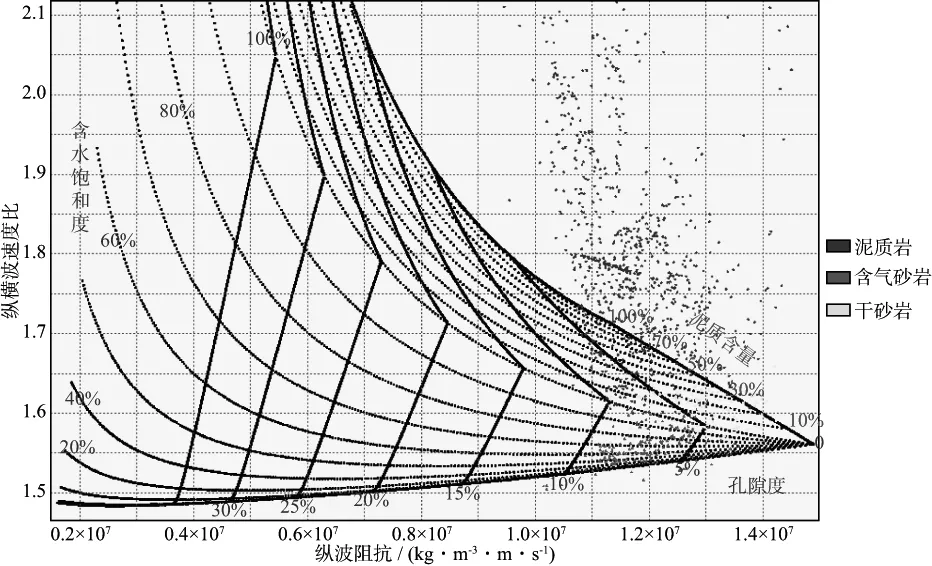
图5 Xu-White模型岩石物理解释模板及W1,W2,W3井弹性参数交会结果

2.3 数据拓展

研究区3口井储层段的弹性参数及储层参数数据有限,并不能涵盖井之外所有的储层参数数据。获取一个全面的储层参数训练数据,是将贝叶斯岩性定量判别推广到地震的必要步骤,因此,需要利用合理的方法对已有的储层参数数据进行拓展。之前研究表明,Xu-White模型最适用于研究区低孔、低渗砂岩的弹性参数正演模拟。经统计,工区山一段储层孔隙度为5%～7%。在Xu-White岩石物理解释模板上,将孔隙度符合该范围、含水饱和度为0～100%的储层数据(即纵横波速度比和纵波阻抗)和原井上的储层数据联合起来,组成全面的储层参数训练数据。

同理,也需要对非储层段的弹性参数数据进行扩充。由于没有适用于模拟研究区泥岩段弹性参数的理论岩石物理模型,本文采用蒙特卡洛多变量数值模拟方法对泥岩的纵横波速度比及纵波阻抗数据进行拓展[33]。该方法利用了变差函数协方差矩阵空间特征的同时,也使模拟结果保留了原数据的空间结构特征,具体方法如下。

1) 以同时模拟纵横波速度比和纵波阻抗为例,分别对两曲线滤波,得到滤波后曲线m1,m2。求取各自原曲线与滤波曲线的差,即残差。

2) 将各自残差数据标准化,使其方差为1。求取各自标准化数据的变差函数γ(d),d=0,1,2,…,n。将变差函数拟合成理论变差模型,如高斯变差模型。由于两变量间具有相关性,变差函数的变程可选择任意两变量的变程之一或均值。

3) 排列N×N理论变差函数的协方差矩阵C,其元素Cij=γ(|i-j|)(i,j=0,1,2,…,n),即:

(16)

4) 求取两变量间的协方差矩阵S。

(17)

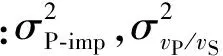
5) 应用Kronecker乘法,计算K。

K=S⊗C

(18)

式中:“⊗”表示Kronecker乘法运算。

6) 对K进行Cholesky分解,得到下三角矩阵R。

K=RRT

(19)

7) 产生随机变向量U,U有2n个样点,服从标准正态分布,计算两变量的最终随机模拟结果:

(20)

式中:VvP/vS,VP-imp分别表示纵横波速度比和纵波波阻抗的数值模拟结果。

以W1井为例,应用该方法数值模拟纵横波速度比及纵波波阻抗数据。如图6所示,仅保留泥岩段数据,将多次模拟结果叠合在交会结果上。从图6 可以看出,随机模拟的数据点符合泥岩的分布特征,可作为泥岩段的拓展数据并入训练样本中。

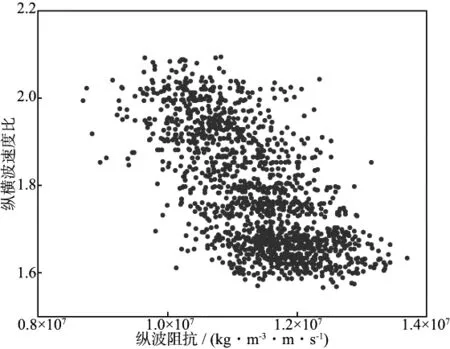
图6 蒙特卡洛多变量数值模拟结果的交会结果

3 贝叶斯岩性判别

3.1 方法原理

贝叶斯公式可表示为:

(21)

式中:x表示单变量或多变量的输入;cj(j=1,2,…,N)表示N个不同的类别;P(cj),P(x|cj)分别为先验概率和条件概率密度函数。

贝叶斯方法在具体的岩性判别应用中,x为单变量或多变量的测井、地震属性;cj表示不同的储层状态类别;P(cj)描述了cj储层状态下的先验概率,可由井数据等统计估算;P(x|cj)为cj储层状态下的条件概率密度函数,由训练数据估算;P(x)为尺度因子,是一个定值;P(cj|x)则表示在一定属性状态下属于某种储层状态的概率。

3.2 一维贝叶斯判别

纵横波速度比及纵波波阻抗的组合能有效区分工区山一段的各类岩性。因此,根据联合测井和拓展的纵横波速度比及纵波波阻抗所组成的训练数据,利用非参数估计方法[6],分别估算干砂岩、含气砂岩及泥质岩类的条件概率密度函数P(x|cj)(图7)。根据研究区目的层段测井资料的统计,干砂岩、含气砂岩、泥岩的先验分布概率P(cj)分别为0.10,0.15,0.75。最后,根据井资料所统计出的各岩性先验分布概率,利用贝叶斯分类判别方法,分别对各井做贝叶斯岩性判别,结果如图8所示,各井每列分别为山一段原始岩性、贝叶斯判别岩性和含气砂岩的概率。从图8可以看到,W1井、W2井各种岩性的判别成功率较高,W3井对于干砂岩的误判稍多。

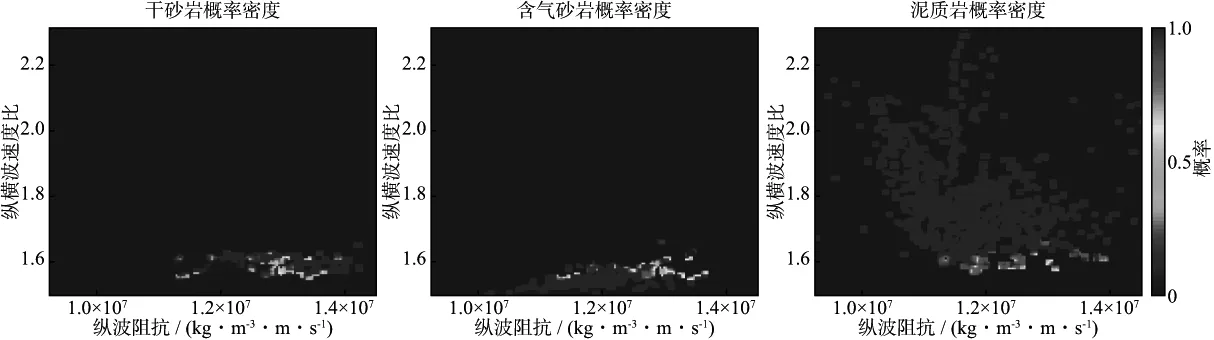
图7 利用非参数估计方法得到的不同岩性条件概率密度函数

图8 利用贝叶斯分类判别方法得到的不同岩性条件概率密度函数

图9显示了不同井位和不同岩性的贝叶斯岩性判别成功率对比结果。从图9a可以看到,结合纵波波阻抗和纵横波速度比的双参数判别各井岩性的成功率最高,运用单参数纵横波速度比判别的成功率次之,而运用纵波波阻抗判别的成功率最低。细分到岩性,从图9b可以看到,运用单参数纵波波阻抗判别泥质岩类及干砂岩误差较大,这是由于两者间的纵波波阻抗值重叠较多;运用单参数纵横波速度比判别泥质岩类和含气砂岩的成功率较高,这是因为两者间纵横波速度比值差别大,容易区分。由于干砂岩在工区中也存在低纵横波速度比的值域分布,仅运用该参数容易将干砂岩误判成含气砂岩,因此判别成功率低。从图9b还可以看出,运用双参数贝叶斯判别,对于干砂岩的判别成功率有了很大提升,进一步验证了多弹性参数贝叶斯判别方法识别岩性的优势。

3.3 二维地震贝叶斯岩性预测

对过W2井的二维地震测线进行叠前、叠后联合反演,获取高质量的纵波阻抗和纵横波速度比数据,尽量减少由地震反演带来的误差和不确定性。基于地震弹性参数数据,利用之前求取的各岩性概率密度函数,进行贝叶斯岩性判别,结果如图10所示。从图10可以看出,W2井山一段储层表现为低纵波波阻抗、低纵横波速度比、贝叶斯岩性判别结果为连续分布的含气砂岩,与实际钻探结果一致,验证了应用岩石物理建模和贝叶斯判别方法预测致密含气砂岩的有效性。

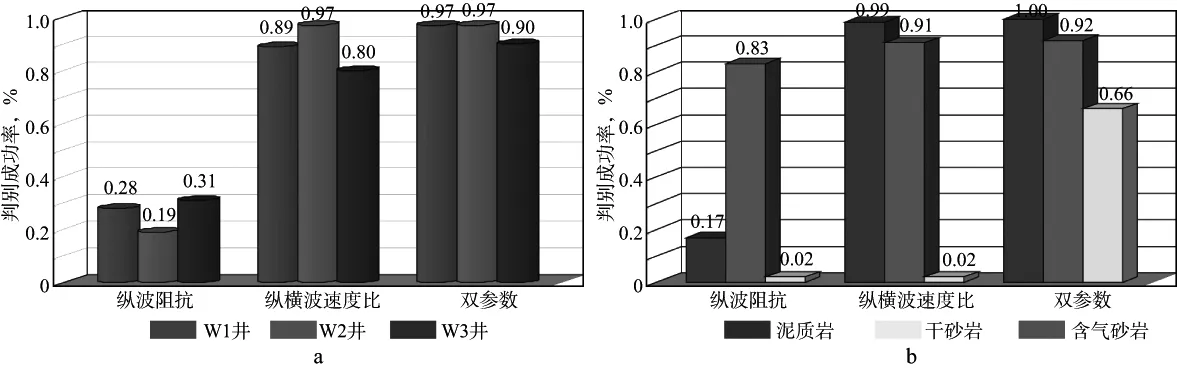
图9 不同井位(a)和不同岩性(b)的贝叶斯岩性判别成功率对比

图10 过W2井的地震纵波阻抗(a)、纵横波速度比(b)及岩性流体预测(c)剖面

本文没有考虑频散效应,而频散因素造成致密储层地震频段和测井频段弹性参数间的差异是不容忽视的问题。目前,常用的Backus平均方法[25]虽从数学角度解决了地震频段和测井频段尺度的问题,但其缺乏物理意义。基于岩石物理理论,建立跨频段岩石物理模型可以定量解决储层频散的问题[34-35],从而能提高储层预测的精度。然而,针对不同类型的储层,如何建立跨频段岩石物理模型工业化应用流程,还需进一步研究。

4 结论

1) 岩石物理建模是岩性及流体概率预测的基础。Xu-White模型最适用于表征工区山一段低孔、低渗含气储层。

2) 与利用单一弹性参数识别有效储层相比,量化对比结果表明,运用多弹性参数贝叶斯判别方法能提升岩性识别的成功率。

3) 蒙特卡洛多变量数值模拟方法计算过程虽复杂,但最大程度地保留了原数据的空间结构特征。在定量地震解释中，当无法利用合适的确定性岩石物理模版来拓展某岩性的岩石物理表征时，可以尝试应用统计岩石物理方法来拓展其岩石物理表征。

4) 叠前弹性参数反演的质量是地震岩性及流体概率预测的关键。实践表明,在各种叠前弹性参数反演算法中,纵波阻抗反演精度最高,通常能满足定量解释的需要。横波阻抗次之,因此需从反演的各个环节,尽可能地提高横波阻抗的反演精度。

[1] Mukerji T,Jørstad A,Mavoko G,et al.Applying statistical rock physics and seismic inversions to map lithofacies and pore fluid probabilities in a North Sea reservoir[J].Expanded Abstracts of 68thAnnual Internat SEG Mtg,1998,894-897

[2] Avseth P,Mukerji T,Mavko G,et al.Statistical discrimination of lithofacies from pre-stack seismic data constrained by well log rock physics:application to a North Sea turbidite system[J].Expanded Abstracts of 68thAnnual Internat SEG Mtg,1998,890-893

[3] Mukerji T,Jørstad A,Avseth P,et al.Mapping lithofacies and pore-fluid probabilities in a North Sea reservoir:seismic inversions and statistical rock physics[J].Geophysics,2001,66(4):998-1001

[4] Avseth P,Mukerji T,Mavko G,et al.Statistical rock physics combing rock physics,information theory,and geostatistics to reduce uncertainty in seismic reservoir characterization[J].The Leading Edge,2001,20(3):313-319

[5] Avseth P,Flesche H,Wijngaarden A.AVO classification of lithology and pore fluids constrained by rock physics depth trends[J].The Leading Edge,2003,22(10):1004-1011

[6] Avseth P,Mukerji T,Mavko G.Quantitative seismic interpretation[M].New York:Cambridge University Press,2005:1-376

[7] Bachrach R.Joint estimation of porosity and saturation using stochastic rock-physics modeling[J].Geophysics,2006,71(5):O53-O63

[8] Spikes K,Mukerji T,Dvorkin J,et al.Probabilistic seismic inversion based on rock-physics models[J].Geophysics,2007,72(5):R87-R97

[9] González E F,Mukerji T,Mavko G.Seismic inversion combining rock physics and multiple-point geostatistics[J].Geophysics,2008,73(1):R11-R21

[10] Bosch M,Mukerji T,Gonzalez E F.Seismic inversion for reservoir properties combining statistical rock physics and geostatistics:a review[J].Geophysics,2010,75(5):75A165-75A176

[11] Grana D,Rossa E D.Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion[J].Geophysics,2010,75(3):O21-O37

[12] Grana D,Dvorkin J.The link between seismic inversion,rock physics,and geostatistical simulations in seismic reservoir characterization studies[J].The Leading Edge,2011,30(1):54-61

[13] Grana D,Mukerji T,Dvorkin J,et al.Stochastic inversion of facies from seismic data based on sequential simulations and probability perturbation method[J].Geophysics,2012,77(4):M53-M72

[14] Grana D,Pirrone M,Mukerji T.Quantitative log interpretation and uncertainty propagation of petrophysical properties and facies classification from rock-physics modeling and formation evaluation analysis[J].Geophysics,2012,77(3):WA45-WA63

[15] Grana D,Paparozzi E,Mancini S,et al.Seismic driven probabilistic classification of reservoir facies for static reservoir modelling:a case history in the Barents Sea[J].Geophysical Prospecting,2013,61(3):613-629

[16] 邓继新,王尚旭.基于统计岩石物理的含气储层饱和度与孔隙度联合反演[J].石油天然气学报,2009,31(1):48-52 Deng J X,Wang S X.Joint inversion of saturation and porosity in gas reservoirs based on statistical rock physics[J].Journal of Oil and Gas Technology,2009,31(1):48-52

[17] 郭伟,何顺利,邓继新.岩石物理在浊积岩储层岩性与气水识别中的运用[J].勘探地球物理进展,2010,33(5):363-371 Guo W,He S L,Deng J X.Application of rock phsics in lithology discrimination and fluid detection of turbidite reservoir[J].Progress in Exploration Geophysics,2010,33(5):363-371

[18] 毛宁波,王浩,谢涛,等.贝叶斯判别法在GD地区叠前地震属性交会中的应用[J].石油天然气学报,2010,32(5):95-98 Mao L B,Wang H,Xie T,et al.Application of Bayesian discretion method of intersection of pre-stack seismic attributes in GD area[J].Journal of Oil and Gas Technology,2010,32(5):95-98

[19] 晏信飞,曹宏,姚逢昌,等.致密砂岩储层贝叶斯岩性判别与孔隙流体检测[J].石油地球物理勘探,2012,47(6):945-949 Yan X F,Cao H,Yao F C,et al.Bayesian lithofacies discrimination and pore fluid detection in tight sandstone reservoirs[J].Oil Geophysical Prospecting,2012,47(6):945-949

[20] 胡华锋,印兴耀,吴国忱.基于贝叶斯分类的储层物性参数联合反演方法[J].石油物探,2012,51(3):225-231 Hu H F,Yin X Y,Wu G C.Joint inversion of petrophysical parameters based on Bayesian classification[J].Geophysical Prospecting for Petroleum,2012,51(3):225-231

[21] 王红伟,陈调顺,刘宝宪,等.鄂尔多斯盆地西南部地区上古生界砂体地震预测及勘探新突破[J].地球物理学进展,2013,28(4):2132-2138 Wang H W,Chen D S,Liu B X,et al.Seismic prediction of sand body in upper Paleozoic and new exploration breakthrough in the southwest Ordos basin[J].Progress in Geophysics,2013,28(4):2132-2138

[22] Kuster G T,Toksöz M N.Velocity and attenuation of seismic waves in two-phase media:part 1,theoretical formulations[J].Geophysics,1974,39(5):587-606

[23] Xu S,White R E.A new velocity model for clay-sand mixtures[J].Geophysical Prospecting,1995,43(1):91-118

[24] Xu S,White R E.A physical model for shear-wave velocity prediction[J].Geophysical Prospecting,1996,44(5):188-195

[25] Mavko G,Mukerji T,Dvorkin J.The rock physics handbook[M].2nded.New York:Cambridge University Press,2009:1-524

[26] 张杨.利用Xu-White模型估算地震波速度[J].成都理工大学学报(自然科学版),2005,32(2):188-194 Zhang Y.Xu-White model for seismic wave velocity prediction[J].Journal of Chengdu Univeristy of Technology(Science & Technology Edition),2005,32(2):188-194

[27] 郭栋,印兴耀,吴国忱.横波速度计算方法与应用[J].石油地球物理勘探,2007,42(5):535-538 Guo D,Yin X Y,Wu G C.Computational approach of S-wave velocity and application[J].Oil Geophysical Prospecting,2007,42(5):535-538

[28] 乔悦东,高云锋,安鸿伟.基于Xu-White模型的优化测井横波速度预测技术研究与应用[J].石油天然气学报,2007,29(5):100-105 Qiao Y D,Gao Y F,An H W.Study and application of optimal technique of shear-wave velocity prediction based on Xu-White model[J].Journal of Oil and Gas Technology,2007,29(5):100-105

[29] 谢月芳,张纪.岩石物理模型在横波速度估算中的应用[J].石油物探,2012,51(1):65-70 Xie Y F,Zhang J.Application of rock physical model in S-wave velocity estimation[J].Geophysical Prospecting for Petroleum,2012,51(1):65-70

[30] 张元中,周开金,赵建斌,等.砂泥岩地层横波测井曲线预测方法研究[J].石油物探,2012,51(5):508-514 Zhang Y Z,Zhou K J,Zhao J B,et al.Shear-wave logging curve prediction method for shaly sand formation[J].Geophysical Prospecting for Petroleum,2012,51(5):508-514

[31] 林凯,贺振华,熊晓军,等.基于基质矿物模量自适应提取横波速度反演方法[J].石油地球物理勘探,2013,48(2):262-267 Lin K,He Z H,Xiong X J,et al.S-wave velocity inversion based on adaptive extraction of matrix mineral modulus[J].Oil Geophysical Prospecting,2013,48(2):262-267

[32] 姜仁,曾庆才,黄家强,等.岩石物理分析在叠前储层预测中的应用[J].石油地球物理勘探,2014,49(2):322-328 Jiang R,Zeng Q C,Huang J Q,et al.Application of rock physics analysis in pre-stack seismic reservoir prediction[J].Oil Geophysical Prospecting,2014,49(2):322-328

[33] Dvorkin J,Gutierrez M A,Grana D.Seismic reflections of rock properties[M].New York:Cambridge University Press,2014:98-100

[34] 巴晶,晏信飞,陈志勇,等.非均质天然气藏的岩石物理模型及含气饱和度反演[J].地球物理学报,2013,56(5):1697-1706 Ba J,Yan X F,Chen Z Y,et al.Rock physics model and gas saturation inversion for heterogeneous gas reservoir[J].Chinese Journal of Geophysics,2013,56(5):1697-1706

[35] Li J Y,Chen X H.A rock-physical modeing method for carbonate reservoirs at seismic scale[J].Applied Geophysics,2013,10(1):1-13

(编辑：顾石庆)

Prediction on lithology and fluid probabilities of tight clastic gas reservoir based on rock physics

Hong Zhong1,2,Zhang Menggang1,Zhu Xiaomin2

(1.NorthwestBranchInstitute,ResearchInstituteofPetroleumExploration&Development,Lanzhou730020,China;2.CollegeofGeosciences,ChinaUniversityofPetroleum,Beijing102249,China)

The tight clastic gas reservoir in China is characterized by low porosity,low permeability and strong heterogeneity.Meanwhile,due to the deep burial depth,the seismic data of tight clastic gas reservoir owns low signal-to-noise ratio and low dominant frequency.The precision of predicting effective gas layer is limited with the aid of a single pre-stack elastic parameter.In order to improve the prediction precision of tight gas reservoir,the rock physical model adaptive to the gas reservoir with low-porosity and low-permeability was established as a fundamental work.Accordingly,the rock physical model based elastic parameter combination sensitive to gas reservoir was selected.Deterministic rock physical model and statistical rock physics method are applied to expand the rock physical characterization of reservoirs and mudstone that are absent in well logging data.Then,the expanded data and original well logging data are integrated to establish probability density function of every type of lithology.Finally,the Bayesian lithological identification method is utilized to predict the lithology and fluid probabilities on the basis of seismic elastic parameter inversion data and probability density functions.The application results show that the Xu-White model is adaptive to characterize the low porosity and low permeability gas sandstone of the target area.Bayesian lithological identification with multiple elastic parameters is able to considerably improve the prediction precision of lithology.The Monte Carlo stochastic simulation of multi-variations can feasibly expand the mudstone rock physical characterization.The final lithology and fluid probability prediction result highly matches the practical production of exploratory wells,which proves that proposed lithology and fluid predicting workflow is helpful in characterizing the tight clastic gas reservoir.

Xu-White model,Monte Carlo stochastic simulation with multi-variations,Bayesian lithology identification,tight clastic gas reservoir

2015-01-30;改回日期：2015-04-21。

洪忠(1985—),男,硕士,主要从事地震解释及储层预测研究工作。

国家自然科学基金项目“陆相坳陷湖盆浅水三角洲地震沉积学模型”(41272133)资助。

P631

A

1000-1441(2015)06-0735-10

10.3969/j.issn.1000-1441.2015.06.012