基于网格分析法的页岩储层等效孔隙纵横比反演
2015-06-24钱恪然李向阳郭诗乐
钱恪然,张 峰,李向阳,3,章 惠,郭诗乐
(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249;2.中国石油大学(北京)CNPC物探重点实验室,北京 102249;3.英国地质调查局,爱丁堡 EH9 3LA,英国;4.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)
基于网格分析法的页岩储层等效孔隙纵横比反演
钱恪然1,2,张 峰1,2,李向阳1,2,3,章 惠4,郭诗乐1,2
(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249;2.中国石油大学(北京)CNPC物探重点实验室,北京 102249;3.英国地质调查局,爱丁堡 EH9 3LA,英国;4.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)
页岩储层通常具有复杂的孔隙空间,等效孔隙纵横比作为描述储层孔隙空间的重要参数,对地层的弹性波速度影响显著。因此,准确预测储层的等效孔隙纵横比对页岩储层建模及横波预测具有重要意义。为了分析页岩储层的等效孔隙纵横比,提出了一种自洽模型与网格分析法相结合的孔隙纵横比反演方法。自洽模型可以利用孔隙纵横比、矿物体积百分比等物性信息来模拟弹性波速度等弹性信息。网格分析法通过将测井值正态分布展开来模拟测量误差,从而降低由测量误差导致的反演不确定性,最终反演得到可靠的孔隙纵横比概率密度分布。通过对北美Barnett页岩储层的实际应用,结果表明,该方法与常规方法相比,其反演结果更加稳定,同时,利用该反演结果还可预测得到较为准确的横波速度。
页岩储层;孔隙纵横比;网格分析法;自洽模型;岩石物理
随着非常规油气勘探的不断发展,页岩勘探已逐步成为物探工作者的研究热点[1-4]。与常规砂岩储层不同,页岩储层通常具有复杂的孔隙结构。复杂的孔隙结构对于页岩的物性和弹性性质均有非常大的影响[5-9],因此,分析页岩的孔隙结构具有重要意义:①复杂的孔隙结构使得页岩储层具有较强的各向异性特征,分析页岩的孔隙结构有助于反演储层的各向异性参数,提高页岩资料处理的精度[10]。②页岩储层通常具有低孔低渗的特征,为了改善储层的孔渗条件,提高页岩气产量,水力压裂是页岩气开发的关键技术之一[11-12]。脆性是指导水力压裂的重要参数,而孔隙结构对储层脆性的影响十分明显。因此,分析页岩的孔隙结构,可以帮助定位脆性层段,进而指导压裂。③游离气是页岩气产量的重要组成类型之一[13],游离气通常附着于页岩储层的微裂缝和裂纹之中。因此,分析页岩的孔隙结构还可以为气藏储量评价提供参考依据。
综上所述,如何准确地模拟和分析页岩的孔隙结构则显得尤为关键。当前,岩石物理学家通过将孔隙结构假想为理想的椭球体,利用椭圆的长、短轴之比来描述孔隙的扁平形态,进而间接地描述复杂的孔隙结构。如Xu-White模型基于泥质含量百分比,将总孔隙分为泥岩相关孔隙和砂岩相关孔隙,并分别用两种不同的孔隙纵横比来描述不同的孔隙类型,达到模拟复杂的孔隙结构的目的[14]。
然而,孔隙纵横比作为一个假想的参数,无法通过测井技术直接测量。因此,在许多岩石物理模型和经验模板的构建中,其通常被设为一个固定的参数[14-15]。虽然这些固定的孔隙纵横比值可以较好的拟合某特定工区的数据资料,但其适用性较差。
为了克服这一缺点,近年来,许多学者逐渐尝试利用各种反演方法来间接反演孔隙纵横比。Yan等[16]利用神经网络算法分别反演了Xu-White模型的两种孔隙纵横比。Xu等[17]基于微分等效理论对Xu-White模型进行修改,使其适用于碳酸盐岩储层,并反演了储层的孔隙类型。Guo等[18]进一步对Xu-Payne提出的碳酸盐岩模型进行改进并将其应用于页岩储层,反演得到页岩储层的孔隙纵横比。
常规的孔隙纵横比反演方法多为穷举法,即,将所有可能的孔隙纵横比值代入已知模型,比较正演模型速度与实测速度,当两者误差极小时所对应的孔隙纵横比即为所求的结果。当测井数据准确时,常规方法可以有效地反演出孔隙纵横比。但是,由于孔隙纵横比对弹性波速度十分敏感,所以当测井数据含有很小的测量误差就会引起较大的孔隙纵横比预测误差。因此,常规穷举法对含有测量误差的测井数据的反演结果并不可靠。为了降低由测量误差引起的预测误差,提高预测结果的可信度,本文引入网格分析法,通过概率统计法提高样本数,将测量误差和模型参数误差对反演结果的影响代入反演流程,由于我们考虑到了可能的误差数据,使得代入反演的样本数提高,降低了反演结果对测量误差的敏感性,提高了反演结果的可信度。最后,将该方法应用于北美Barnett页岩储层某井的实际数据,并讨论了测量误差对反演结果的影响。应用结果显示网格分析法与常规方法相比,可以得到更为稳定的反演结果。
1 方法原理
1.1 自洽理论
包裹体理论将孔隙假想为理想的椭球体,并用孔隙纵横比来控制孔隙的形态,使得通过理论公式来描述复杂的孔隙结构成为可能。因此,包裹体理论被广泛运用于页岩岩石物理建模中。
自洽理论(self-consistent approximation,SCA)是典型的包裹体等效介质理论,该理论最早由Norris等[19]提出,理论的基本思路是将需要模拟的复杂介质中各个矿物组分及孔隙当成相互独立的单一相,将多相介质放置在一个弹性参数可调的背景介质中,且背景介质无限大。通过调整背景介质的弹性参数,使其不断接近多相介质,直至当有一平面波入射时,多相介质不发生散射,此时背景介质的弹性模量等同于多相介质的弹性模量。SCA的等效示意图如图1所示,灰色和蓝色的椭球体为不同的矿物相,黑色的扁平椭球体为孔隙,灰色的背景介质为假想的等效介质。现今应用最广泛的是Berryman[20-21]提出的N相混合物的自洽近似公式:
(1)
(2)
(3)
(4)
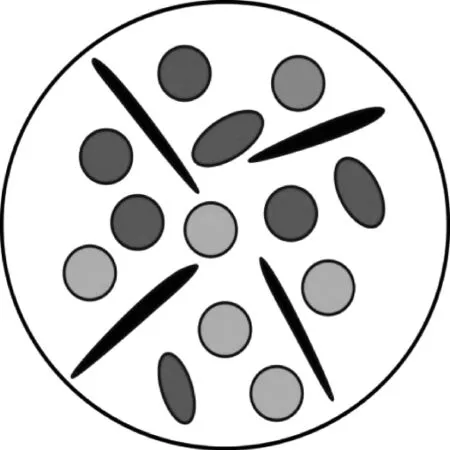
图1 SCA等效理论示意
1.2 孔隙纵横比敏感性分析
如前所述,现阶段针对页岩储层孔隙纵横比的反演研究仍沿用碳酸盐岩孔隙结构的反演思路[17-18,22-25]。反演主要包括正过程和反过程两部分,正过程主要指将测井资料获得的确定的矿物组分百分比、孔隙度等物性参数和可变的孔隙纵横比输入岩石物理模型,计算得到相应的模型P波速度(vP_m)和模型S波速度(vS_m)。而反过程则是利用实测的弹性波速度与正过程计算得到的模型速度相比较,当实测速度与模型速度误差最小时,所对应的孔隙纵横比即为所求结果。
由于孔隙流体的弹性张量与矿物的弹性张量差别较大,所以改变孔隙纵横比对岩石的性质(如速度)的影响十分显著,换而言之,孔隙纵横比对速度的敏感性较强。为了验证孔隙纵横比的敏感性,我们将表1中给出的Barnett页岩储层的平均矿物体积百分比和其他物性参数输入SCA模型,得到的正演P波速度vP_1,此时各相的纵横比均为1。接着,将各包裹体的纵横比依次从1变成0.01,而不改变其他的参数,此时得到的正演P波速度记为vP_0.01。vP_gap=vP_1-vP_0.01则反映了改变某一相的纵横比对最终等效速度的影响。
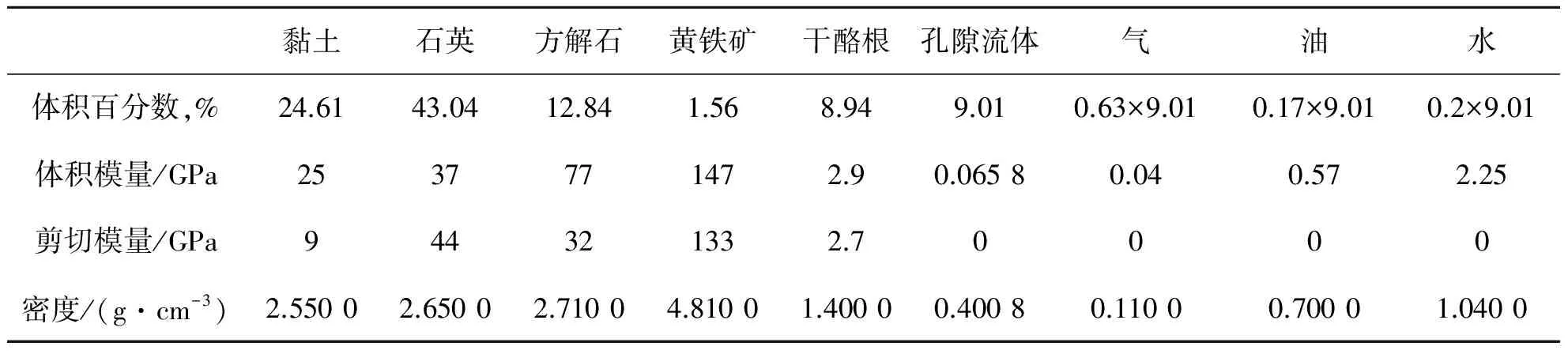
表1 Barnett页岩储层各矿物物性参数(引自Mavko岩石物理手册[29])
图2反映了改变单一纵横比对等效速度的影响,纵坐标为vP_gap,横坐标表示不同的包裹体。由图可知,改变孔隙纵横比对最终等效速度的影响远大于其它相。因此,相比较而言,孔隙纵横比是影响最终等效速度的主要参数。
因此在常规反演流程中,孔隙纵横比的反演结果比较依赖于反过程中实测速度的准确性,如何避免由于测量数据精度不高而带来的纵横比反演的不确定性是一个值得思考的问题。网格分析法作为一种概率统计方法,使得讨论孔隙纵横比的不确定性成为可能。
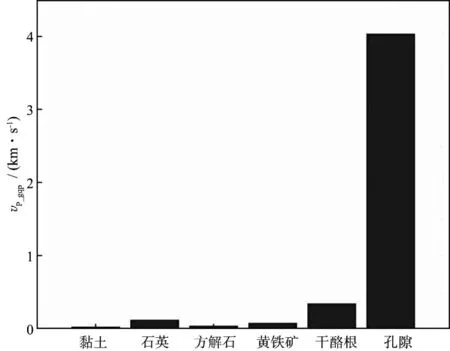
图2 改变不同包裹体的纵横比对等效速度的影响
1.3 网格分析法
网格分析法是一种概率统计方法[26],近年来被应用于地球物理反演中[27-28],用来降低反演结果的不确定性。在反演过程中,网格分析法模拟了一组可能的观测值,该组数据满足正态分布且以实测值为期望,使得反演过程以实测数据为先验信息,同时考虑了测量误差的影响。最终比较模拟值与正演值,满足一定目标函数的正演值被采纳,最终得到待反演参数的概率密度分布。
该方法通过正态分布模拟增加了样本数,使得在反演过程中,考虑了潜在的测量误差。得到的反演结果也由原来的单一值改进为该参数的发生概率。因此,该方法可以较好地降低反问题中由于测井数据测量不准导致的反演结果的不准确性。本文中,由于待反演参数(孔隙纵横比)对拟合参数(弹性波速度)较为敏感,所以更能体现该方法的优势。
本文将SCA等效理论与网格分析法相结合,对Jiang[27]提出的反演流程进行了改进,进一步提高了反演的准确性,具体流程如图3所示。
该流程需要在每个深度重复,主要步骤可以归纳为:
1) 通过测井资料获取每个深度的矿物组分和孔隙度,将孔隙度正态分布展开,期望为实测值φobs,标准差为0.02,采样点数为100。
2) 将正态分布展开后的孔隙度、矿物组分及可变的孔隙纵横比输入SCA模型。孔隙纵横比的变化范围0~1,变化间隔为0.001。由于孔隙度的正态分布采样点数为100,且每个孔隙度值和每个孔隙纵横比值对应一个正演结果。因此,可以得到100×1000个模拟P波速度(vP_m)。
3) 通过测井资料获取每个深度的P波速度,将测量值正态分布展开,期望为测量值vP_obs,标准差为0.1,采样点数为100。
4) 将所有模拟的P波速度(vP_m)与正态分布后的实测速度(vP_obs)比较,当满足目标函数|vP_m-vP_obs|<0.01时,该模型速度所对应的孔隙纵横比即被采纳。
5) 每个孔隙纵横比对应的采纳次数除以所有孔隙纵横比的采纳次数即为每个孔隙纵横比的发生概率。
分别对实测的孔隙度和P波速度进行正态分布展开,由于测量值最有可能接近真实值,所以将正态分布的期望设为测量值本身。同时,假设孔隙度测井和速度测井值的误差范围大约为2%和0.1km/s,因此,将误差设为正态分布的标准差。正态分布的采样点数影响着反演结果的精度以及计算效率。通过试验发现,当标准差取100时,能达到精度和计算效率的相对平衡。同时,正态分布的标准差还决定着网格的长度,当速度和孔隙度正态分布展开后,正演结果将与一个网格内的所有正态分布值进行比较。因此,可以形象地将这种搜索算法称为网格搜索法。

图3 孔隙纵横比概率密度反演流程
2 实际资料应用效果分析
2.1 研究区介绍
所用资料的目标层位为Barnett页岩层。Barnett页岩层是美国著名的高产页岩气层。Barnett地层含有较多的脆性矿物(如石英和长石的体积达到35%~50%),而黏土矿物较少[11]。因此,该地层是水力压裂的有利地层。同时,Barnett页岩层的上覆地层为Marble Falls层,下伏地层为Ellenburger层。上、下地层的孔隙度均明显小于目的层段,这为气藏的储存形成了天然的屏障。
图4为Barnett页岩层某井的测井曲线。通过岩心分析和测井解释报告可知,目的层具有较典型的页岩层测井响应特征。具体表现为高自然伽马值、低弹性波速度、高孔隙度以及低密度的特征。
2.2 孔隙纵横比模板建立
前文已阐述了孔隙纵横比对于页岩储层评价的重要性,在此,基于SCA等效理论建立孔隙纵横比的反演模板,并利用网格分析法来反演Barnett页岩层的孔隙纵横比。
根据测井报告和岩心数据,可计算得到Barnett储层的平均矿物百分比和平均孔隙度(如表1所示)。表1的第2列至第6列分别表示Barnett储层的5种主要矿物组分的体积百分比、体积模量、剪切模量以及密度,所有的物性参数值均引自Mavko的岩石物理手册[29]。利用Barnett页岩层段的35个岩心的孔隙流体分析结果,计算得到目的层段孔隙流体的平均体积百分比分别为:气63%,油17%,水20%。利用Wood公式,我们可以计算得到三相流体混合后的等效流体性质,如表1 第7列所示。
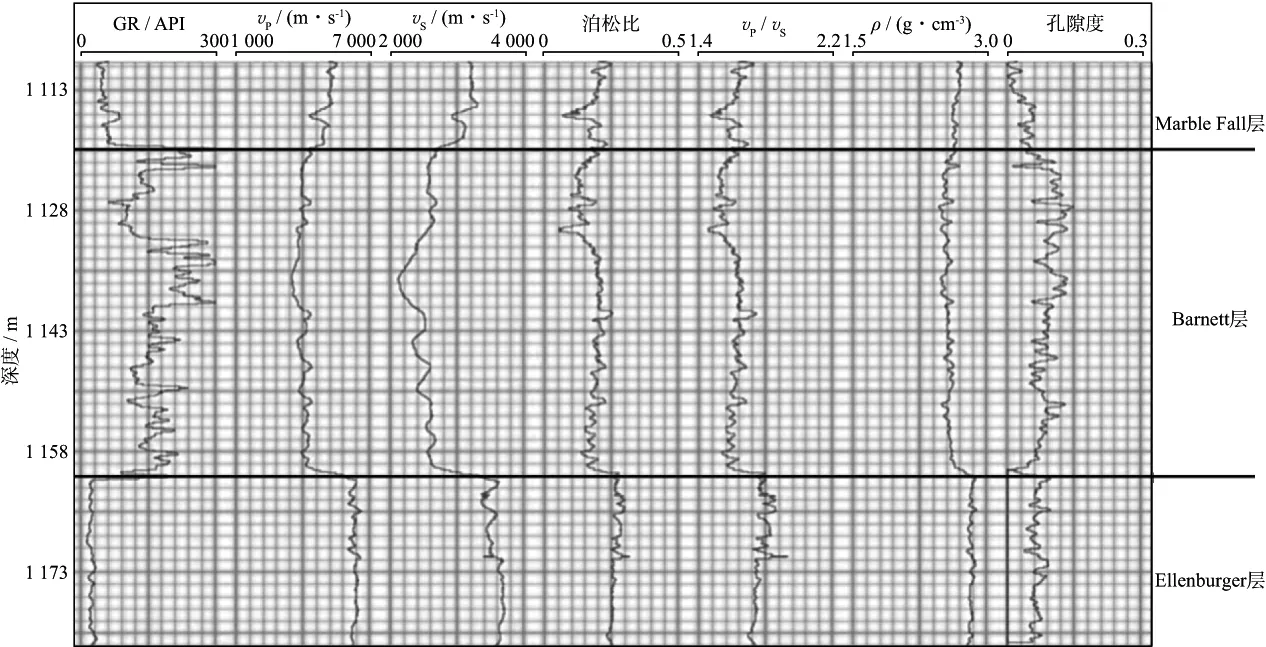
图4 Barnett页岩储层测井曲线
由于等效速度对孔隙纵横比的敏感程度远高于其他矿物组分的纵横比,因此在反演孔隙纵横比时,可以将其他矿物的纵横比粗略地设为定值。在本文中,我们将黏土、石英、方解石、黄铁矿和干酪根的纵横比均设为1。
将表1中各矿物的体积百分比、弹性参量和纵横比输入SCA模型,同时改变孔隙度和孔隙纵横比,得到如图5a所示的孔隙纵横比反演模板。模板的横轴为孔隙度,纵轴为P波速度。背景色为孔隙纵横比,暖色代表高孔隙纵横比,冷色代表低孔隙纵横比。黑色的点为目的层段的实际数据点。通过模板所示,模拟的P波速度随着孔隙度的增加而减小,同时也随孔隙纵横比的减小而减小。图5b 反映了不同孔隙纵横比时所对应的实际孔隙形态。
2.3 孔隙纵横比反演
利用已构建的孔隙纵横比反演模板(图5a),并结合网格分析法,对目的储层的孔隙纵横比进行反演。
按照图3的反演流程,首先将每个深度的孔隙度正态分布展开,期望为实测值φP_obs,标准差为0.02,采样点数为100。图6a为孔隙度曲线,图6b为正态分布展开后的孔隙度曲线。背景色为概率密度。
随后,将声波速度测井曲线正态分布展开,期望为测量值vP_obs,标准差为0.1,采样点数为100。如图7所示,图7a为测井值vP,图7b为以测井值为期望展开的概率密度分布曲线,背景色为概率密度。
此时,图5a的反演模板就演变为图8的网格分析模板。从图中可以看到,每个黑色的点代表每个深度的测井值,当孔隙度和P波速度分别以正态分布展开后,单个的数据点也展开为一个网格(如粉色所示)。每一个粉色网格内所包含的背景色所对应的孔隙纵横比,都是该深度点的可能孔隙纵横比。
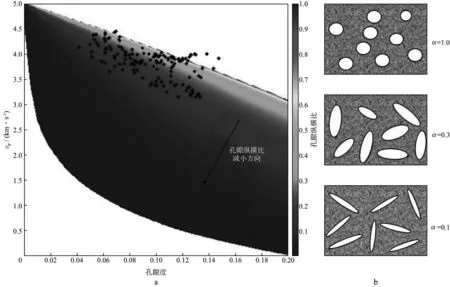
图5 基于SCA理论计算得到的孔隙纵横比反演模板(a)及不同孔隙纵横比对应的页岩孔隙形态(b)
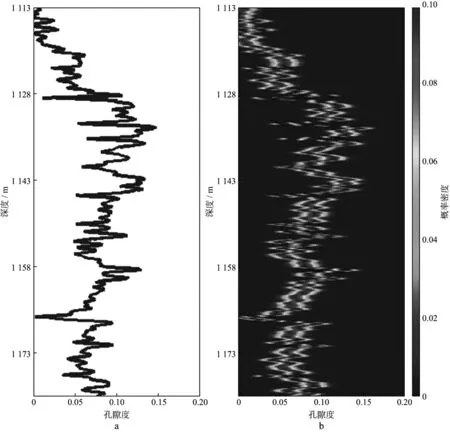
图6 实测孔隙度曲线(a)和正态分布展开后的孔隙度概率密度分布(b)
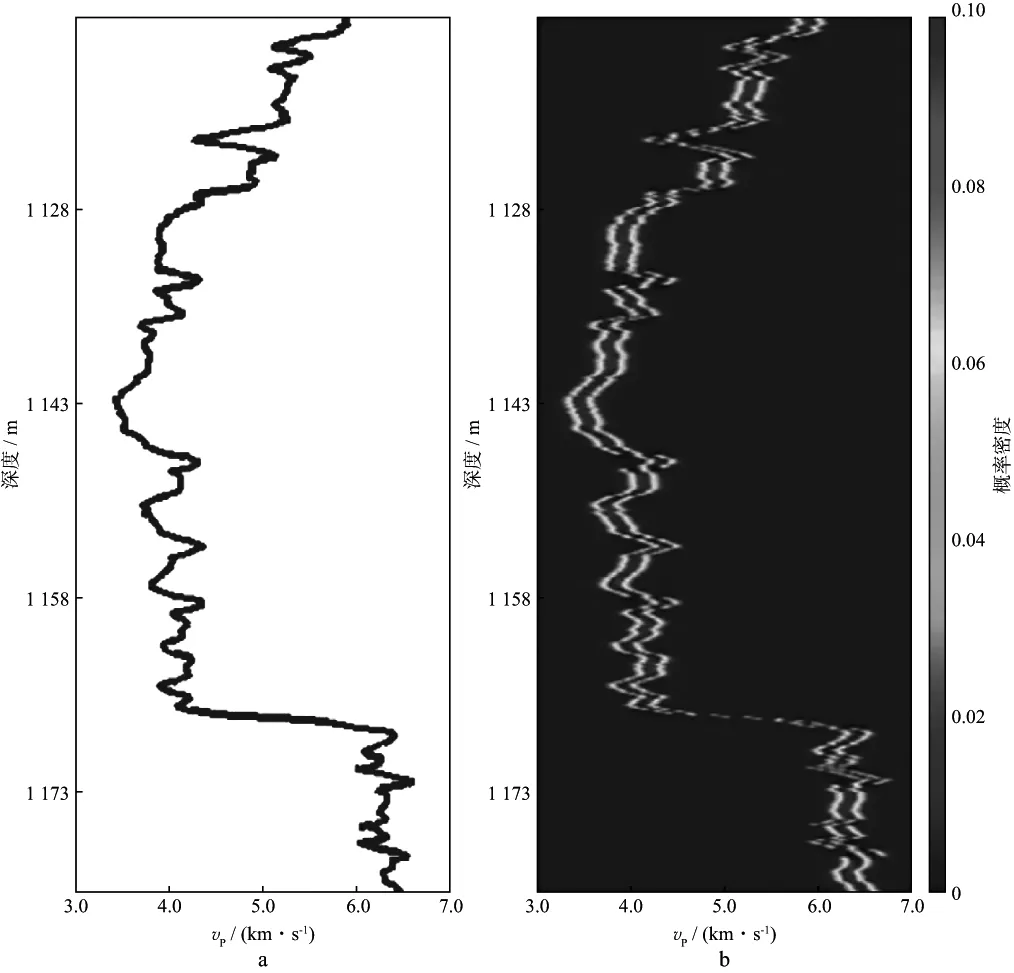
图7 实测纵波速度曲线(a)和正态分布展开后的纵波速度概率密度分布(b)
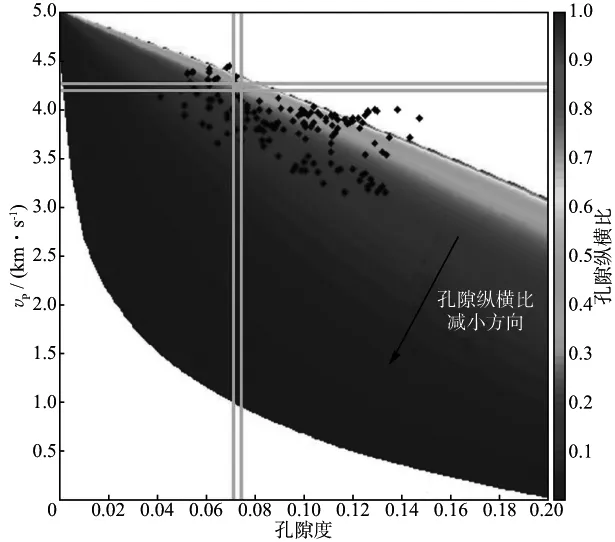
图8 基于岩石物理模板的网格分析法示意(粉色矩形为所设网格)
孔隙纵横比的变化范围0~1,每个深度的孔隙度满足正态分布,采样点数为1000。由于每个孔隙度值和每个孔隙纵横比值对应一个正演结果。因此,可以得到100×1000个模拟P波速度(vP_m)。将所有模拟的P波速度(vP_m)与正态分布后的实测速度(vP_obs)比较,当满足目标函数|vP_m-vP_obs|<0.01时,该模型速度所对应的孔隙度即被采纳。每个孔隙纵横比对应的采纳次数除以所有孔隙纵横比的采纳次数即为每个孔隙纵横比的发生概率。
与常规方法比较,网格分析法考虑了更多误差可能性。以图8为例,常规方法将测井得到的孔隙度和速度投影到模板上后,该点所对应的背景色的数值即为待求的孔隙纵横比。而网格分析法以测井得到的孔隙度和速度作为网格中心构建一个网格(如粉色矩形所示),网格的长和宽分别由孔隙度和速度的测量误差决定。网格内所有的背景色所对应的值都有可能是该深度点的待求孔隙纵横比。换而言之,常规方法是将一个点(即测量的真实值)代入模板反演,最终得到一个准确的反演值。而网格分析法是将一个网格内所有的点都代入模板,最终得到待反演参数所有可能性的发生概率。当网格的长和宽都为1时,网格分析法即简化为常规方法。
图9为最终的孔隙纵横比反演结果,黑色直线标注出了目的页岩储层(Barnett储层)。Barnett储层深度为1120.140~1164.366m,上覆地层为Marble Fall储层,下伏地层为Ellenburger地层。图中横坐标为孔隙纵横比,纵坐标为深度,背景色表示孔隙纵横比的发生概率。同时,为了对比网格搜索法和常规反演方法的预测结果,我们考虑了网格长和宽为1时的特殊情况(此时网格分析法即简化为常规方法),常规方法的反演结果如红色曲线所示。
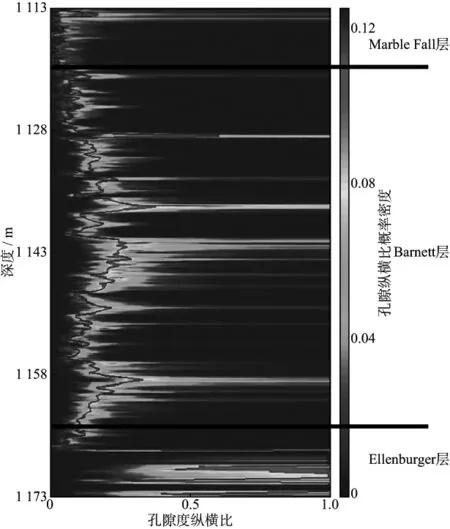
图9 反演得到的孔隙纵横比概率密度分布
从目的层段的反演结果来看,红色曲线的变化趋势和背景色极大值的变化趋势基本相同,说明该井段的数据资料较好,常规方法和网格分析法都具有反演页岩储层孔隙纵横比的能力。为了验证反演结果的可靠性,我们将利用纵波速度作为约束参数反演得到的每个深度孔隙纵横比概率密度的极大值作为等效纵横比,输入SCA模型,正演得到预测的横波速度,并与实测横波速度相比较(如图10a所示),红实线表示实测横波速度,蓝虚线代表预测的横波速度。同时,将横波速度作为目标参数反演得到孔隙纵横比,进而预测纵波速度,预测结果如图10b所示。可以发现预测结果与实测结果吻合较好,验证了反演结果的可靠性与实用性。
2.4 孔隙纵横比概率密度误差分析
与常规方法相比,网格分析法不但可以提供最优的孔隙纵横比反演值,还可以提供反演参数的概率密度信息(如图9背景色所示)。为此,将进一步分析概率密度反演结果,并讨论测量误差对反演结果的影响。
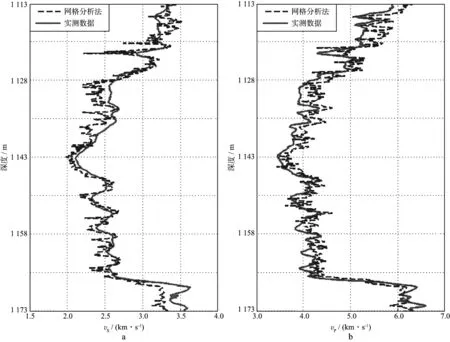
图10 实测横波速度和预测横波速度对比(a)以及实测纵波速度和预测纵波速度对比(b)
如上所述,网格分析法是统计类反演法,常规方法为确定性反演方法。通常情况下,确定性方法只能得到唯一解,而统计算法能够提供更多的信息。统计算法通过增加样本数,达到缩小置信空间增加反演结果可信度的目的。然而,统计算法由于提供了更多解的可能性,如何确定解的非唯一性和稳定性是需要面对的问题。
针对本文讨论的具体问题,我们将假想的测量误差分别代入速度和孔隙度测井数据,以此来分析当测量数据含有噪声时,常规方法与网格分析法反演结果的稳定性。
基于图9的分析可知,网格分析法与常规方法的反演结果总体较为吻合。因此,假设测井数据无误差。同时,由于在图3的反演流程中速度和孔隙度的正态分布标准差分别被设为0.10和0.02,意味着网格分析法假设的速度和孔隙度的误差范围分别为±0.1km/s和±2%,因此,我们分别将±0.1km/s和±2%的随机干扰加入速度和孔隙度测井曲线,并重复图3的反演流程,最终的反演结果如图11所示。
图11a和图11b分别为加噪前、后的反演结果,红实线为常规反演结果。对比图11可以发现,网格分析法的结果(特别是每个深度的概率密度最大的极值点)在加噪前后变化不大,而常规方法的反演结果则差别较大。常规方法的预测结果在加噪后表现得更为震荡,整体值略高于加噪前,且局部出现奇异值(如白色箭头所示)。这表明在加噪以后,网格分析法表现得更为稳定。同时,常规方法的预测结果偏离了概率密度的极大值,但其仍在概率密度的预测范围之内,这可能是由于随机噪声范围(±0.1km/s和±2%)满足网格分析法的正态分布所导致的结果。
此外,对某一深度而言,概率密度值的范围通常随孔隙纵横比的增大而增大(例如1143.00m附近的概率密度结果较为分散,而1150.62m深度处的结果相对集中)。需要指出的是,分散的概率密度结果并不能反映该深度的孔隙含有多种孔隙纵横比,这可能是由统计算法的多解性所造成。为了验证加入噪声后反演结果的可靠性,我们将利用P波作为约束条件计算得到的孔隙纵横比重新输入模型,将计算得到的横波速度与实测横波速度进行比较,结果如图12所示,其中蓝虚线为网格分析法的预测结果,黑实线为常规方法的预测结果,红实线为实测S波速度。
由图12可知,加噪前,除了个别异常点外,网络分析法预测的横波速度与常规方法预测的横波速度均接近实测数据。而加噪后,常规方法受噪声的干扰较大,而网格分析方法仍能得到较为准确的结果。特别是对于概率密度较为分散的深度段(黑色箭头所示),由于常规方法预测得到孔隙纵横比较大,因此,与其对应的横波速度预测值也相对较高。
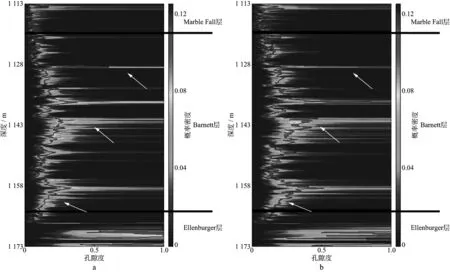
图11 加噪前(a)、后(b)孔隙纵横比概率密度分布与常规反演结果(红色实线)对比
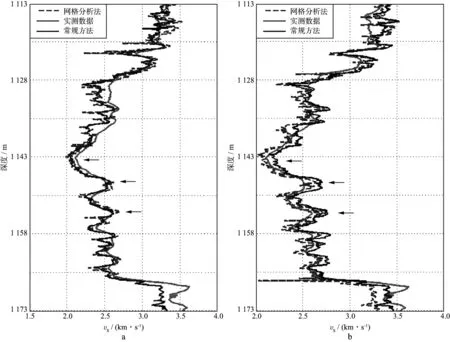
图12 加噪前(a)、后(b)实测横波速度与通过反演结果计算的预测结果对比
3 结论与认识
本文介绍了一种基于SCA等效理论和网格分析法的页岩储层孔隙纵横比反演方法。网格分析法通过将实测测井值正态分布展开,将测井的误差考虑进反演算法中,最终得到待反演参数的概率密度分布。降低了由测量值不准引起的预测误差,提高了预测结果的可信度。最后,将该方法应用于北美Barnett页岩储层的测井数据,反演得到较为可靠的孔隙纵横比概率密度分布,并利用反演结果预测了目的层的弹性波速度。
此外,由于页岩储层的孔隙结构十分复杂,真实的孔隙结构远比模型更为复杂,本文对孔隙类型的讨论也仅限于地层满足模型假设的前提条件。同时,本文只利用了常规的测井资料进行分析。若工区具有更多的非常规资料(如成像测井等),则可以构建更为准确的岩石物理模型,进而得到更加可靠的孔隙结构信息。最后,网格分析法虽然提供了更多的有效信息,但同时也增加了计算量。在今后的研究中,需要寻找精度与效率之间的平衡点。
[1] 董宁,霍志周,孙赞东,等.泥页岩岩石物理建模研究[J].地球物理学报,2014,57(6):1990-1998 Dong N,Huo Z Z,Sun Z D.et al.An investigation of a new rock physics model for shale[J].Chinese Journal of Geophysics,2014,57(6):1990-1998
[2] 孙赞东,贾承造,李相方.非常规油气勘探与开发[M].北京:石油工业出版社,2011:1-1348 Sun Z D,Jia C Z,Li X F.Unconventional oil and gas exploration and development[M].Beijing:Petroleum Industry Press,2011:1-1348
[3] 张金川,金之钧,袁明生.页岩气成藏机理和分布[J].天然气工业,2004,24(7):15-18 Zhang J C,Jin Z J,Yuan M S.Reservoir mechanism of shale gas and its distribution[J].Natural Gas Industry,2004,24(7):15-18
[4] 于炳松.页岩气储层孔隙分类与表征[J].地学前缘,2013,20(4):211-220 Yu B S.Classification and characterization of gas shale pore system[J].Earth Science Frontiers,2013,20(4):211-220
[5] 印兴耀,刘欣欣,曹丹平.基于Biot相洽理论的致密砂岩弹性参数计算方法[J].石油物探,2013,52(5):445-451 Yin X Y,Liu X X,Cao D P.Tight sandstone elastic parameters calculation method based on Biot consistent theory[J].Geophysical Prospecting for Petroleum,2013,52(5):445-451
[6] 印兴耀,李龙.基于岩石物理模拟的纵横波速度反演方法[J].石油物探,2015,54(3):249-253 Yin X Y,Li L.P-wave and S-wave velocities inversion based on rock physics model[J].Geophysical Prospecting for Petroleum,2015,54(3):249-253
[7] 胡起,陈小宏,李景叶.基于各向异性岩石物理模型的页岩气储层横波速度预测[J].石油物探,2015,54(3):254-261 Hu Q,Chen X H,Li J Y.Shear wave velocity prediction for shale gas reservoirs based on anisotropic rock physics model[J].Geophysical Prospecting for Petroleum,2015,54(3):254-261
[8] 未晛,王尚旭,赵建国,等.致密砂岩纵、横波速度影响因素的实验研究[J].石油物探,2015,54(1):9-16 Wei X,Wang S X,Zhao J G,et al.Laboratory investigation of influence factors on vp and vs in tight sandstone[J].Geophysical Prospecting for Petroleum,2015,54(1):9-16
[9] 赵群,曲寿利,薛诗桂,等.碳酸盐岩溶洞物理模型地震响应特征研究[J].石油物探,2010,49(4):351-358 Zhao Q,Qu S L,Xue S G,et al.Study on the seismic response characteristics on the physical model of carbonate cave[J].Geophysical Prospecting for Petroleum,2010,49(4):351-358
[10] Sayers C M.The effect of kerogen on the elastic anisotropy of organic-rich shales[J].Geophysics,2013,78(2):D65-D74
[11] Guo Z Q,Li X Y,Liu C,et al.A shale rock physics model for analysis of brittleness index,mineralogy and porosity in the Barnett Shale[J].Journal of Geophysical Engineering,2013,10(2):1-10
[12] 杨心超,朱海波,崔树果,等.P波初动震源机制解在水力压裂微地震监测中的应用[J].石油物探,2015,54(1):43-50. Yang X C,Zhu H B,Cui S G,et al.Application of P-wave first-motion focal mechanism solutions in microseismic monitoring for hydraulic fracturing[J].Geophysical Prospecting for Petroleum,2015,54(1):43-50
[13] 董宁,许杰,孙赞东,等.泥页岩脆性地球物理预测技术[J].石油地球物理勘探,2013,48(增刊1):69-74 Dong N,Xu J,Sun Z D,et al.Shale brittleness prediction by geophysical methods[J].Oil Geophysical Prospecting,2013,48(S1):69-74
[14] Xu S,White R E.A new velocity model for clay-sand mixtures[J].Geophysical Prospecting,1995,43(1):91-118
[15] Xu S,White R E.A physical model for shear-wave velocity prediction[J].Geophysical Prospecting,1996,44(4):687-717
[16] Yan J,Li X Y,Liu E R.Effects of pore aspect ratios on velocity prediction from well-log data[J].Geophysical Prospecting,2002,50(3):289-300
[17] Xu S,Payne M A.Modeling elastic properties in carbonate rocks[J].The Leading Edge,2009,28(1):66-74
[18] Guo Z Q,Li X Y,Chapman M.Correlation of brittleness index with fractures and microstructure in the Barnett Shale[J].Expanded Abstracts of 74thEAGE Annual Conference,2012,F022
[19] Norris A N,Sheng P,Callegari A J.Effective-medium theories for two-phase dielectric media[J].Journal of Applied Geophysics,1985,57(6):1990-1996
[20] Berryman J G.Long-wavelength propagation in composite elastic media[J].The Journal of the Acoustical Society of America,1980,68(6):1820-1831
[21] Berryman J G.Mixture theories for rock properties[C]∥Ahrens T J.Rock physics & phase relations:a handbook of physical constants.Washingtong D C,USA:American Geophysical Union,1995:205-228
[22] 张金强,曲寿利,孙建国,等.一种碳酸盐岩储层中流体替换的实现方法[J].石油地球物理勘探,2010,45(3):409-442 Zhang J Q,Qu S L,Sun J G,et al.A fluid substitution realization method in carbonate reservoir[J].Oil Geophysical Prospecting,2010,45(3):409-442
[23] Kumar M,Han D H.Pore shape effect on elastic properties of carbonate rocks[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005,1477-1481
[24] Ruiz F,Chen A.A rock physics model for tight gas sand[J].The Leading Edge,2010,29(12):1484-1489
[25] 原宏壮.各向异性介质岩石物理模型及应用研究[D].山东:中国石油大学,2007 Yuan H Z.Study of anisotropic rock physics model and application[D].Shandong:China University of Petroleum,2007
[26] Sen M,Stoffa P L.Global optimization methods in geophysical inversion[M].New York,USA:ELSEVIER Science Publishers B V,1995:1-281
[27] Jiang M,Spikes K T.Estimation of the porosity and pore aspect ratio of the Haynesville Shale using the self-consistent model and a grid search method[J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012,1-5
[28] Jiang M,Spikes K T.Estimation of reservoir properties of the Haynesville Shale by using rock-physics modelling and grid searching [J].Geophysical Journal International,2013,195(1):315-329
[29] Mavko G,Mukerji T,Dovrkin J.The rock physics handbook[M].New York,USA:Cambridge University Press,2009:1-524
(编辑:朱文杰)
Inversion of effective pore aspect ratio for shale reservoir using grid search method
Qian Keran1,2,Zhang Feng1,2,Li Xiangyang1,2,3,Zhang Hui4,Guo Shiyue1,2
(1.StateKeyLaboratoryofPetroleumResourceandProspecting,ChinaUniversityofPetroleum,Beijing102249,China;2.CNPCKeyLaboratoryofGeophysicalProspecting,ChinaUniversityofPetroleum,Beijing102249,China; 3.BritishGeologicalSurvey,EdinburghEH9 3LA,UK;4.SinopecGeophysicalResearchInstitute,Nanjing211103,China)
The pore spaces of shale reservoir are usually complicated.Effective pore aspect ratio is a significant parameter to characterize pore spaces of formations,which obviously impact the elastic velocities of formations.Therefore,the accurate estimation of effective pore aspect ratio for shale reservoir is meaningful in rock physics modeling and S-wave velocity prediction.In order to estimate the pore structure of tight formation,a workflow is proposed for pore aspect ratio inversion by combining self-consistent approximation (SCA) method and grid search method.Elastic properties of formation can be estimated by inputting physical parameters,such as pore aspect ratio and mineral concentration,to SCA model.Grid research method can reduce the uncertainty during the inversion of pore aspect ratio by normally distributing the logging data.The combination of two methods can enhance the stability of inversion results.The workflow is performed to the Barnett shale reservoir in North America,and the results provide us a robust prediction of pore aspect ratio.Finally,the S-wave velocity can be predicted accurately by using the inverted pore aspect ratio.
shale formation,pore aspect ratio,grid search method,self-consistent approximation model,rock physics
2015-05-05;改回日期:2015-08-13。
钱恪然(1988—),男,博士在读,现主要从事页岩储层岩石物理建模研究工作。
国家重点基础研究发展计划(973计划)项目(2013CB228603)和国家自然科学基金项目(U1262208,41204072,41474096)联合资助。
P631
A
1000-1441(2015)06-0724-11
10.3969/j.issn.1000-1441.2015.06.011
