随机型混流双边装配线仿真分析

段移庭

(广东工业大学 机电工程学院，广州 510006)

装配线可以分为单边装配线 (只使用一边)和双边装配线 (左侧和右侧同时使用)两大类［1］。在实际生产中的应用，例如大型产品、汽车、冰箱等，与单边装配线相比，双边装配线具有能缩短装配线长度，减少产品的下线时间，降低工具、夹具及物料处理的成本等优点［1－2］。混流双边装配线能够快速响应市场的高速变化，以最低的生产成本和最高的生产效率满足产品多样化的需求［3］。根据作业时间的特点可以将混流双边装配线分为确定型和随机型，确定型混流双边装配线平衡问题研究主要是在关于产品如何投产排序、如何实现平准化，达到负荷均衡的目的［4］;然而，现实生产情况中往往会遇到很多不确定的因素，例如工人不确定的装配作业时间，机器故障影响等等，这些都会影响到实际的生产效率［5］。所以考虑作业时间因素的影响，能够更加接近实际的生产情况。

在已求得确定型混流双边装配线平衡问题的排序结果基础上，通过eM－Plant仿真软件建立模型，考虑作业时间不确定因素，对所建立的模型进行仿真。根据仿真结果分析随机因素对混流双边装配线平衡的影响。

1 混流双边装配线问题描述

以文献［6］中某公司生产冰箱的混流双边装配线作为研究对象，文中构建了冰箱的双边混流装配线平准化和投产排序模型，并对模型求解，得到了合理的平衡方案结果。该混流双边装配线平衡模型描述如下:主要有A、B、C、D四种产品需要被装配，它们所需求的比例分别为6∶6∶5∶5，装配线节拍为20，作业元素优先关系如图1所示。文献 ［6］在不考虑工人不确定的装配时间、机器故障等的影响情况下，得到了确定型混流双边装配线平衡方案。该模型平准化方案如下:装配线共被分配9个成对工作站，18个工作站，开启使用15个工作站，共需操作人员16个;该模型的投产排序结果如下所示:AA－BB－DD－CC－DD－BB－AA－CC－BB－DD－CC－AA－BB－AA－CC－DD－BB－AA－CC－DD－BB－AA。

2 随机型混流双边装配线仿真建模

为了分析不确定因素对装配线平衡的影响，在文献［6］已有的模型基础上加入装配时间随机分布的因素，即考虑工人行走、机器故障不确定时间而影响作业时间的现象。在研究混流双边装配线平衡的问题中，作业时间不确定性的随机因素对线平衡的影响问题很难通过数学建模和求解的方法来处理［7］，笔者采用离散随机事件仿真方法来对作业不确定性随机因素对装配线平衡的影响进行分析。eM－Plant是一个面向对象的图形化的建模和仿真集成软件，可以应用于制造系统的仿真、优化［8－9］。

图1 作业元素优先关系图

采用eM－Plant仿真软件对随机混流双边装配线进行仿真建模及分析。图2为用eM－Plant仿真软件对混流双边型装配线所建的仿真模型，图2中，Source为冰箱装配线仿真模型的冰箱主件进口，在此设定实体的到达模式和排队规则 (即产品的投放比例，可以通过表格T设定)，其中Assembly i(i=1，2，…，9)为装配线各个工作站，该模型一共9组工作站，Process为工作站组的单个工作站 (单边)。主件实体按照确定的比例等时间间隔到达并按照先进先出 (FIFO)的排队规则接受装配线的服务。

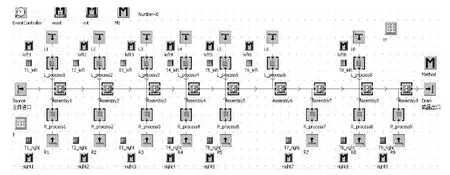
图2 混流双边装配线仿真模型

假设装配时间服从某种正态分布，均值为表1中各工作站各个产品的装配时间，方差为0.8。

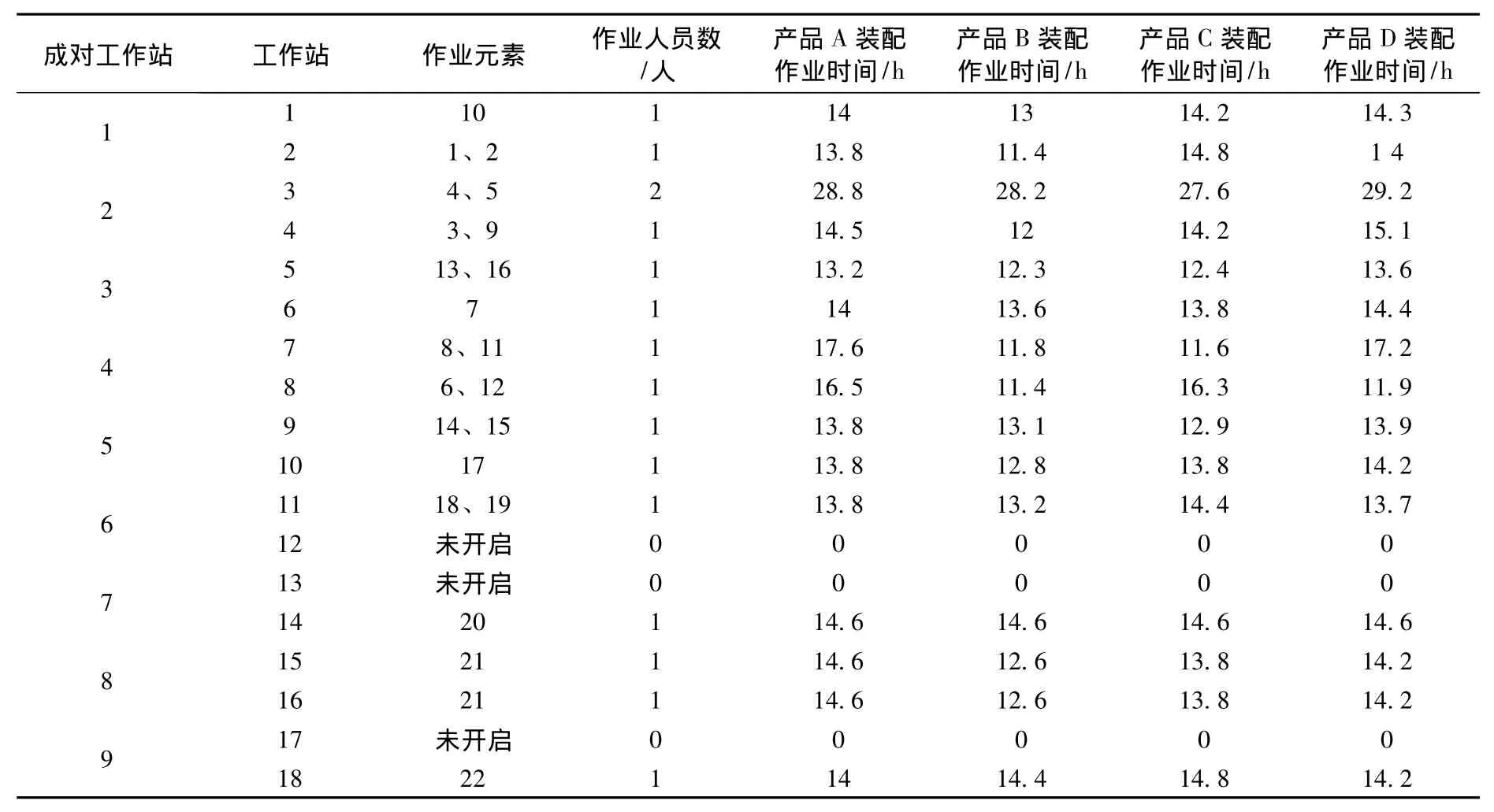
表1 混流双边装配线平衡分配的结果

所考虑的随机因素是作业时间的不确定性，产品在工作站中装配处理的模式 (服务时间分布情况)由Process来定义，根据不同产品处理时间的模式分别来设置不同的概率分布。例如产品A在工作站1中的装配作业分布为:N(14，0.8)，可以通过Method程序 (left)来判断和控制产品A在工作站1中作业模式，如下:

模型中表格Ti(i=1，…，9)用来记录不同产品在不同工作站的处理时间，表格TF用来统计各个工作站组的作业时间和装配线的平衡率。

3 仿真模型运行与结果分析

建立的仿真模型的仿真时间为8 h，启动运行后，任意截取运行时间为2 h 7 min时的装配线状况如图3所示。从图3中可以看出工作站8处于等待空闲状态，说明该分配方案在考虑作业时间随机性的特点后，对装配线平衡产生了影响，下面再观察装配线平衡率的情况。

图3 混流双边装配线仿真模型运行状态

图4为截取的运行结果数据统计表格，图中表格第一列到第九列分别统计不同产品在各个工作站组的平均装配作业时间，第10列统计的是不同产品的装配线平衡率。从图4中可以看出，当装配线线趋向稳定后，平衡率仅为71%，因此该平衡方案在考虑随机作业时间因素后，不再是最佳平衡结果，仍然有改善空间。

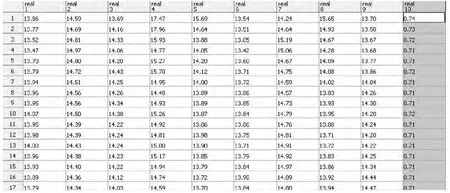
图4 仿真运行结果

4 结语

在现有确定型混流双边装配线的基础之上，考虑到实际装配过程会遇到的不确定因素:不确定的装配作业时间，建立了随机型混流双边装配线模型。仿真结果表明，加入随机扰动后，影响了装配线上各工作站的平衡状况，出现工位等待现象，从而说明，在研究双边装配线平衡过程中，不能忽视随机因素带来的影响。所以，后续的研究需要在加入随机因素后继续求解混流双边装配线平衡方案。

［1］Bartholdi J．Balancing two － sided assembly lines:A case study［J］．International Journal of Production Research，1993．31(10):2447 －2461．

［2］Qin X M．A heuristic method for two-sided assembly line balancing problem［J］．Journal of Shanghai Jiaotong University，2005，10(1):61 －65．

［3］陈心德，吴忠．生产运作管理［M］．北京:清华大学出版社，2005．

［4］Christian B，Armin S．A survey on problems and methods in generalized assembly line balancing［J］．European Journal of Operational Research，2006，168:694 －715．

［5］刘凯，苏平，赵卫．考虑工人行走的作业时间随机分布的U型线平衡［J］．工业工程，2012，15(4):124－130．

［6］杨涛．双边混流装配线平准化及其在冰箱装配中应用［D］．杭州:浙江工业大学，2010．

［7］李东，汪定伟．基于仿真的优化方法综述［J］．控制工程，2008(6):672－677．

［8］施於人．eM-Plant仿真技术教程［M］．北京:科学出版社，2009．

［9］于兆勤．混合型装配线平衡问题的不确定性仿真研究［J］．中国机械工程，2008，19(11):1297－1302．