海冰动力过程的改进离散元模型及在渤海的应用
2015-06-24季顺迎王安良米丽丽刘煜李宝辉
季顺迎,王安良,米丽丽,刘煜,李宝辉
(1. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116023;2. 国家海洋环境预报中心 国家海洋局海洋灾害预报技术研究重点实验室,北京 100081)
海冰动力过程的改进离散元模型及在渤海的应用
季顺迎1,王安良2,米丽丽1,刘煜2,李宝辉2
(1. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116023;2. 国家海洋环境预报中心 国家海洋局海洋灾害预报技术研究重点实验室,北京 100081)
海冰的断裂、重叠和堆积等离散分布特性广泛地存在于极区和副极区的不同海域,并对海冰的生消、运移过程有着重要影响。针对海冰在不同尺度下的离散分布特点,发展海冰动力过程的离散元方法有助于完善海冰数值模式,提高海冰数值模拟的计算精度。为此,本文针对海冰生消运移过程中的非连续分布和形变特性,发展了适用于海冰动力过程的改进离散元模型(MDEM)。不同于传统离散元方法,该模型将海冰离散为具有一定厚度、尺寸和密集度的圆盘单元。海冰单元设为诸多浮冰块的集合体,其在运移和相互接触碰撞过程中,依照质量守恒发生单元尺寸、密集度和厚度的相应变化。基于海冰离散性和流变性的特点,该模型采用黏弹性接触本构模型计算单元间的作用力,并依据Mohr-Coulomb准则计算海冰法向作用下的塑性变形及切向摩擦力。为验证该模型的可靠性,本文对海冰在规则水域内的运移和堆积过程进行了分析,离散元计算结果与解析值相一致;此外,对旋转风场下海冰漂移规律的模拟进一步验证了本文方法的精确性。在此基础上,对渤海辽东湾的海冰动力过程进行了48 h数值分析,计算结果与卫星遥感资料和油气作业区的海冰现场监测数据吻合良好。在下一步工作中将考虑海冰离散元模拟中的热力因素影响,发展具有冻结、断裂效应的海冰离散元模型,更精确地模拟海冰动力-热力耦合作用下的生消和运移过程。
海冰动力学;离散元模型;堆积冰;渤海
1 引言
近年来,随着极区海冰覆盖面积和冰量的急剧变化,海洋资源开采向寒区的不断延伸,北极夏季航道的初步开通,海冰这一自然现象及其引发的工程灾害引起了人们更加密切的关注。海冰在极区与大气、海洋的相互作用是影响全球气候演变趋势的重要因素,在渤海、Baltic海和Okhotsk海等副极区海域又是影响油气开发、冰区航运和水产养殖的重要环境条件[1—3]。海冰在不同尺度下均表现出很强的离散分布特性,如大中尺度下的非连续流变行为,以及小尺度下的断裂、重叠和堆积现象[4—8]。为对不同尺度下海冰的动力-热力过程进行精确、高效的数值模拟,需要针对海冰的离散分布规律及其动力学特性建立相适应的数值方法和本构模型。
自20世纪70年代以来,对极区及副极区的海冰演化过程进行数值模拟,人们分别建立了欧拉坐标下的有限差分法(FDM)[9—12]、拉格朗日坐标下的光滑质点流体动力学方法(SPH)[13—14],以及两种坐标相结合的质点网格法(PIC)[15—18]。在以上数值方法中,FDM方法是发展最早,也是目前应用范围最广的海冰数值方法,并已应用于北极、Baltic海和渤海等海域[9—10,12,19]。最近,有限体积法、有限元方法、质量点法和混合拉格朗日-欧拉法等也被应用于海冰的动力学数值计算[20—23]。在海冰动力学的数值方法中,一般采用黏塑性[9,12,24—25]、弹塑性[26]或黏弹塑性[14,27—28]本构模型进行海冰内力的计算。特别是,光滑质点流体动力学方法可有效克服因网格差分而产生的平流项扩散的现象[29—30],可提高对局地海域海冰动力现象模拟以及边缘线预测的精度,而被引入到海冰动力学过程的数值模拟中。
上述数值方法均将海冰视为连续介质,能够理想地模拟海冰在宏观尺度下的流变特性和平均分布状态,具有计算效率高的特点。然而,大量的现场监测和卫星遥感资料表明,海冰在极区及其冰缘区、副极区等不同海域均表现出很强的离散分布特性,且平整冰、堆积冰、冰脊和水道相互交织出现[31—33]。冰块尺寸在不同尺度下有很大的变化范围,可从极区大尺度下的100 km以上到小尺度下的1 km以下[3,34]。在波浪作用下,海冰还可破碎为10 m甚至更小的冰块。海冰的这种离散分布特性早在20世纪80年代初就得到了人们的重视,并明确指出海冰具有类似颗粒材料的力学行为[4,35]。Shen等最早将颗粒流理论应用到海冰动力学中,建立了海冰碰撞流变学,并用于碎冰区的海冰动力学数值模拟[36]。针对海冰的离散分布特性,基于颗粒介质理论的海冰动力学本构模型也相继发展起来[37-38]。但这些本构模型并不能考虑细观尺度下海冰的分布形态、碰撞接触作用,其计算参数也没有考虑海冰类型、冰块尺寸等细观因素的影响。最近,Hopkins的一系列研究表明,海冰离散元模型不但可用于小尺度下冰块间的碰撞作用,中尺度下冰脊、冰隙的演化规律,甚至还可对极区大尺度下的海冰动力过程进行数值模拟[39—40]。在以上海冰的离散元模型中,依据海冰的分布状态将其离散成多个具有厚度、尺寸和速度的计算单元。当考虑冰块冻结时,该方法还能够合理地模拟海冰动力学过程中的断裂、重叠和堆积现象,具有物理意义明确、计算精度高的优点。然而,由于海冰在不同尺度下分布形态的差异以及相互作用的复杂性,对非规则形状海冰单元的构造,以及单元间的接触碰撞模型还需要进一步研究。
近年来,离散元模型的发展和完善对其在海冰动力学数值模拟中的应用有很大的促进作用。但也注意到,离散元模型在海冰动力方程的计算中采用显式计算,时间步长小,其计算效率明显低于其他计算模型,目前还不能满足海冰数值预报和长期海冰动力学模拟的时效要求。此外,采用传统的离散元方法需要对每个冰块建立相应的计算模型。由于海冰单元数目巨大,这在当前计算条件下难以实现;对每个冰块的初始位置、尺寸、厚度等参数进行精确确定也是目前海冰监测技术不能达到的。为此,基于海冰动力学SPH数值模拟的思路,将每个海冰单元设为诸多浮冰块的集合体,其刚度设为密集度的函数并考虑海冰单元的塑性变形。通过对传统海冰离散元模型进行改进可对海冰动力学过程进行相对精确、高效的数值模拟。
本文通过发展海冰动力过程的改进离散元模型,对不同边界条件下海冰运移、堆积过程进行数值分析以检验该模型的可靠性。通过对辽东湾海冰动力演化过程的离散元模拟,对油气作业区的海冰参数进行提取,并与现场海冰监测资料进行了对比分析,进一步验证改进离散元模型的有效性和精确性。
2 海冰动力过程的改进离散元模型
在海冰动力学的改进离散元模型中,海冰单元设为诸多冰块的集合体,相互接触、碰撞作用受其平均厚度、密集度、单元尺寸等参数影响。当单元间的法向应力超过其压缩强度时,海冰发生塑性变形,并由此导致单元尺寸的变化。海冰单元的运动规律受控于风和流的拖曳力、海面倾斜引起的海冰压强梯度力、冰间作用力等因素。
2.1 海冰单元的运动方程
海冰的运动主要受控于单元间的作用力、风和流的拖曳力、科氏力,以及海面倾斜引起的压强梯度力,其动力方程由牛顿定律来描述,即:
(1)
式中,M为单位面积海冰质量,即M=NρiHi,V为海冰速度矢量,f为科氏参数,且f=2ωesinφ,ωe为地球转角速度,φ为地理纬度,K为垂直于海面的单位矢量,ξw为瞬时海面梯度,海冰在单位面积上风和流的拖曳力为Vai和Vwi,其中Ca和Cw为风和流的拖曳系数,Vai和Vwi为相对于海冰的风速和流速矢量,·σ为海冰单元间相互作用引起的单位面积上的内力矢量。
2.2 海冰单元间的接触模型
海冰单元之间的作用力主要包括单元间在法向和切向上因相互重叠而引起的弹性力和因相对速度引起的黏性力。此外,切线方向上还需考虑基于Mohr-Coulomb准则的滑动摩擦。海冰单元MA和MB间的接触模型如图1所示,其中Kn和Kt分别为海冰单元间的法向和切向刚度系数,Cn和Ct分别为海冰单元间的法向和切向黏性系数。
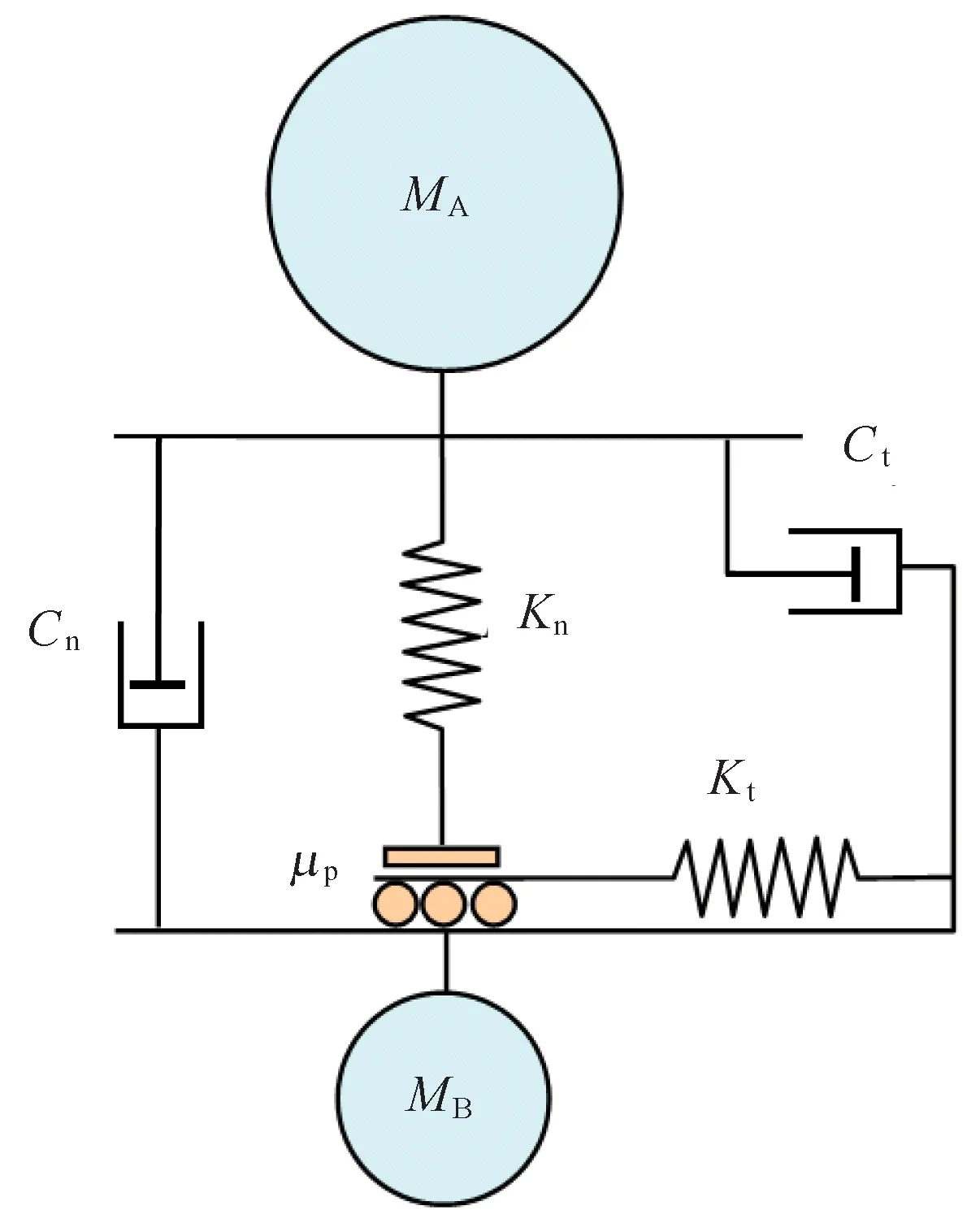
图1 海冰单元间的接触模型Fig.1 Contact model of sea ice elements
在法线方向,海冰单元间的接触力为:
(2)

在切线方向,基于Mohr-Coulomb摩擦定律,海冰单元的作用力为:
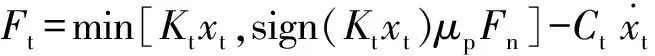
(3)

海冰单元的法向和切向刚度与其密集度密切相关。这里依据河冰和海冰力学性质与其密集度的对应关系,可取[14,41]:
(4)
式中,E为海冰弹性模量,Hi为海冰厚度,Ni为海冰单元的密集度,Nmax为其最大值,这里取Nmax=100%,j值通常取为15。此外,海冰力学参数还可设为密集度的负指数函数[9]。在离散元模型中,一般取单元的切向刚度Kt=0.5Kn。
海冰单元的黏性系数Cn可由其质量、法向刚度和无量纲黏性系数确定,即[42]:
(5)

当采用线黏弹性模型计算海冰单元的作用力时,两个自由单元间的接触时间被定义二元接触时间,即[42]:
(6)
式中,Tbc为海冰单元的二元接触时间,即两个海冰单元从碰撞到分离的接触时间。在线黏弹性模型中,它是一个与单元大小和材料性质相关的常数,其可用于确定海冰动力学计算的时间步长Δt。一般取时间步长Δt为二元接触时间Tbc的1/50。
2.3 海冰单元的塑性变形
当海冰单元在外力作用下相互挤压时,单元间的法向应力可由法向力Fn和接触面积S确定,即σn=Fn/S。在海冰动力学的改进离散元模型中,海冰单元为诸多碎冰块的集合体。其法向压缩强度可根据单元内浮冰块在竖直方向上的静水压力,并由Mohr-Coulomb摩擦定律进行确定[14,39]。该方法已成功地应用于海冰动力学的SPH数值模拟中[13—14]。当海冰单元的法应力超过其压缩强度时,将会发生塑性形变。相应地,海冰单元将缩小,并引起单元密集度和厚度的改变。
依据颗粒材料的塑性失效准则并考虑冰内静水压力效应,海冰单元的压缩强度σc写为[41]:
(7)
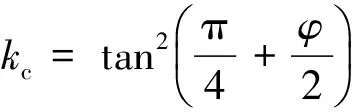
(8)
式中,ρi,ρw分别为海冰和海水的密度,g为重力加速度。
当海冰单元发生塑性形变后,其面积会相应减小,并由此导致密集度的增加,海冰发生辐合现象。当海冰密集度达到最大值Nmax时,若海冰内力进一步增大,此时单元内的海冰将发生堆积现象。相反,当海冰单元间的应力小于其压缩强度时,海冰单元在静水压力作用下发生辐散现象,并由此导致海冰单元面积的增加和密集度的降低。该海冰在内力作用下的辐合和辐散过程示意图如图2所示。在该辐合和辐散过程中,海冰单元的质量保持恒定,而其面积、密集度和厚度发生相应变化。

图2 海冰辐合-辐散过程及海冰单元相应面积、密集度的变化Fig.2 Divergent and convergent processes and the corresponding area,concentration of sea ice elements
3 规则区域内海冰动力过程的数值模拟
为验证MDEM模型的可靠性和准确性,下面分别对规则区域内两个典型的海冰动力过程进行数值分析。一是变宽度水道中海冰在风和流拖曳下的漂移和堆积过程,另一个是矩形区域内海冰在旋转风场作用下的动力过程。
3.1 变宽度水道内海冰的漂移和堆积过程
在海冰动力学研究中,水道内海冰漂移和堆积的动力过程分析是检验海冰数值方法的一个有效途径,其平均冰厚的分布特征得到了现场观测数据、室内模型实验和理论模型解析解的验证[23,41,43—44]。在此基础上,本文采用变宽度水道形式,并在水道内放置一个障碍物。通过分析海冰的绕流特征进一步检验改进离散元模型对海冰动力过程模拟的适用性。
本文采用的变宽度水道如图3所示,总长度L=170 km,左侧和右侧宽度分别为W1=30 km和W1=14 km。海冰初始厚度Hi0=1.0 m,初始密集度Ni0=100%,冰区初始长度L1=30 km,其他主要计算参数列于表1中。数值模拟的第1 d、2 d、3 d和7 d的海冰单元速度矢量和平均厚度分布如图4所示。在风和流的作用下,海冰绕过三角形障碍物向右漂移,并在右侧边界发生堆积。堆积高度随时间的推移而不断增加,由此导致海冰内力不断增强。当海冰内力与风、流的拖曳力达到平衡时,海冰单元运动趋于静止,堆积高度达到稳定。在海冰漂移和堆积过程中,海冰单元的速度、尺寸和厚度均发生改变。

图3 变宽度水道内海冰的初始分布Fig.3 Initial distribution of ice cover in a various-width channel
表1 海冰动力过程的改进离散元模拟中主要计算参数
Tab.1 Main computational parameters in MDEM simulation of sea ice dynamic processes

参数定义数值参数定义数值E弹性模量/MPa100μp海冰单元间摩擦系数0 5Ca风的拖曳系数0 0015Cw流的拖曳系数0 0045Va风速/m·s-120 0Vw流速/m·s-10 0

续表1

图4 不同时刻的海冰速度和平均冰厚分布Fig.4 The distribution of ice velocity and average ice thickness at different time
以上结果表明,海冰单元在风和流的驱动下向右侧漂移过程中,海冰的速度、厚度不断变化。特别在第1 d绕过三角形障碍物过程中,海冰在障碍物附近的速度明显减小,冰厚也相对较厚。在障碍物后方形成一个明显的水域,海冰呈现显著的绕流特性。此外,受水道边界摩擦的影响,边界附近的冰速明显减小,其平均冰厚也小于水道中部冰厚。
为进一步验证模型对冰厚模拟的准确性,这里将海冰稳定后的平均厚度与解析解进行对比。本文海冰稳定条件是指海冰颗粒单元的速度的最大值接近于零。考虑边界摩擦时,海冰的稳态堆积高度可由经典的冰坝理论计算[27]。它将海冰应力在水道宽度方向进行平均,并通过求解风和流的拖曳力、海冰内力以及边界摩擦力的平衡方程确定海冰的堆积高度,即[14]:
(9)
式中,Hi0为海冰的初始厚度,B为水道的宽度,这里参照图3知B=W2。
将以上水道内海冰厚度的离散元模拟结果与式(9)的解析解列于图5中,可以发现平均冰厚与解析解有较高的拟合度,由此验证了改进离散元模拟在海冰动力学模拟中的准确性。
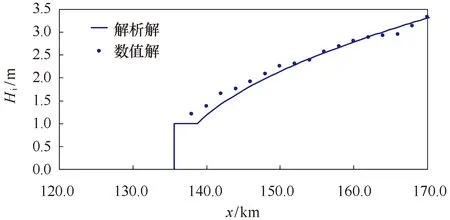
图5 海冰平均厚度的离散元计算值与解析解的对比分析Fig.5 Comparison of average ice thickness simulated with DEM to analytical solution
3.2 旋转风场作下海冰动力过程
为检验海冰动力学数值方法的有效性,Flato建立了经典的旋转风场作用下的海冰运动算例[15]。在500 km×500 km的计算域内,风场中心位于(250 km,220 km)处,海冰初始分布于计算域的上半区域,如图6所示。海冰初始厚度Hi0=1.0 m,初始密集度Ni0=80%,海冰单元的初始直径D0=4.0 km。计算域中位置r处的风速为:
(10)
式中,W为风速矢量,K为垂直水面的单位向量,r和r分别为计算域中任一点的位置矢量与其到风场中心的距离,风速参数ω=0.5×10-3rad/s,λ=8×105m2/s。

图6 旋转风场及海冰初始分布Fig.6 The initial distribution of sea ice in rotational wind field
采用改进离散元模型对旋转风场作用下的海冰动力过程进行了10 d数值计算,第2 d、5 d、10 d的冰速和平均冰厚分布如图7所示。可以发现,海冰在风和流的拖曳作用下在旋转风场内围绕风场中心做涡旋运动。在海冰运动过程中,左侧边界附近的海冰单元与边界发生挤压和堆积使平均冰厚增加,而右侧边界附近的海冰单元因远离边界漂移使平均冰厚减小;此外,从平均冰厚的等值线分布可以发现,在涡旋中心两侧会形成两个明显的涡,并在海冰漂移过程中发生移动和变形。以上计算结果表明,改进的离散元模型可对旋转风场作用下海冰的动力演化过程进行精确数值模拟。
4 渤海海冰动力过程的数值模拟
为进一步验证改进离散元模型在海冰动力学模拟中的适用性,下面将其用于渤海海冰动力演化过程的数值分析,并通过海冰卫星遥感资料和油气作业区海冰监测数据对计算结果进行检验。
4.1 辽东湾海冰分布的演化
在海冰动力学的MDEM模拟中,气象条件采用辽东湾JZ20-2平台上实测的时间间隔为10 min的风速,水文条件采用Leendertse二维非线性长波模式在欧拉坐标计算得到的潮流场。
海冰初始冰厚和密集度可由油气平台的海冰现场监测图像和卫星遥感图像提取[45—47]。这里对2010年1月22日10时50分的卫星遥感图像进行海冰的参数提取。海冰卫星遥感图像如图8a所示,由此提取的海冰单元分布如图8b所示,其颜色定性地表示海冰单元的局部厚度。依据辽东湾JZ20-2油气平台上实测的海冰厚度,由海冰单元参数确定的海冰厚度和密集度分布如图8b~d所示。在海冰动力学模拟中,海冰单元的初始直径为2.0 km,共有5 618个单元,其他主要计算参数取表1中的数值。通过采用改进离散单元模型对海冰动力过程的48 h数值模拟,海冰单元位置、海冰密集度、冰厚和冰速分布分别如图9和10所示。
从模拟结果可以发现,海冰单元位置分布规律与卫星遥感资料基本一致。在数值模拟的48 h内,风速在2~8 m/s之间,气温在-5~-8℃之间,气象条件变化平缓,海冰运动主要受控于潮流,且冰厚受热力因素影响较小。对于海冰的动力过程,MDEM方法较好地模拟了辽东湾海冰的动力演化规律。它通过对海冰单元在拉格朗日坐标下的运移、碰撞和重叠特性的离散元分析,通过改变单元的位置、尺度、密集度和冰厚等海冰参数,较精确地描述海冰的运移过程。特别是,它通过对海冰单元漂移速度和运动轨迹的数值计算,能较准确地确定冰缘线位置,而不存在欧拉坐标下的数值扩展现象。
但我们也发现模拟的冰缘线面积较实际冰缘线面积略大。这主要是因为由拉格朗日坐标下海冰单元向欧拉坐标下海冰参数的等值线插值过程中,有一个向外扩散的趋势。此外,本文采用MDEM方法对海冰演化过程中尚未考虑热力因素的影响,还需在后续工作中进一步完善以更合理地模拟海冰的生消和运移过程。

图7 旋转风场作用下海冰速度和平均冰厚分布Fig.7 Distributions of ice velocity and average ice thickness in the rotational wind field
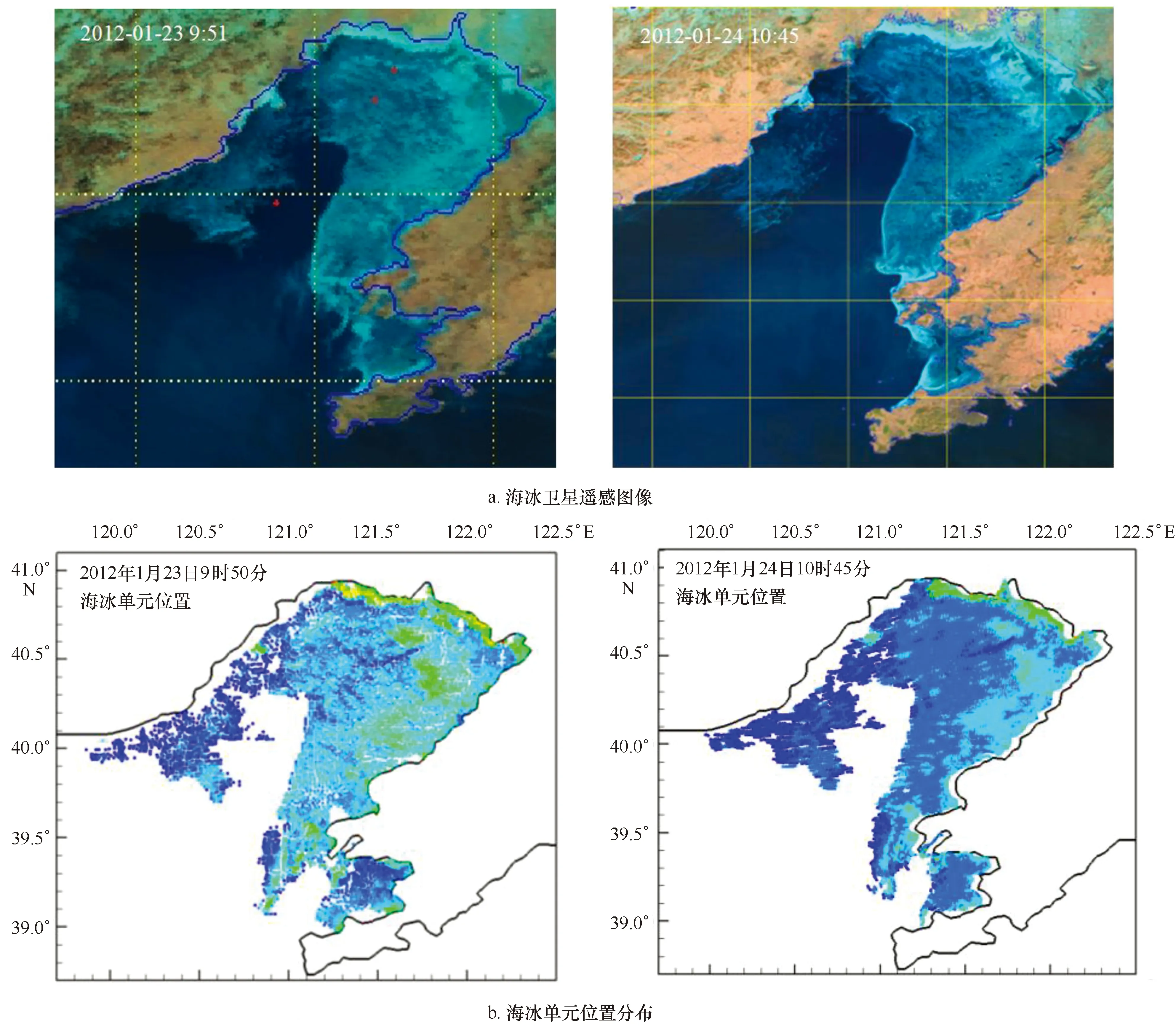
图9 海冰卫星遥感图像及MDEM模拟的海冰位置Fig.9 Satellite images of sea ice and the simulated location of sea ice elements with MEDM
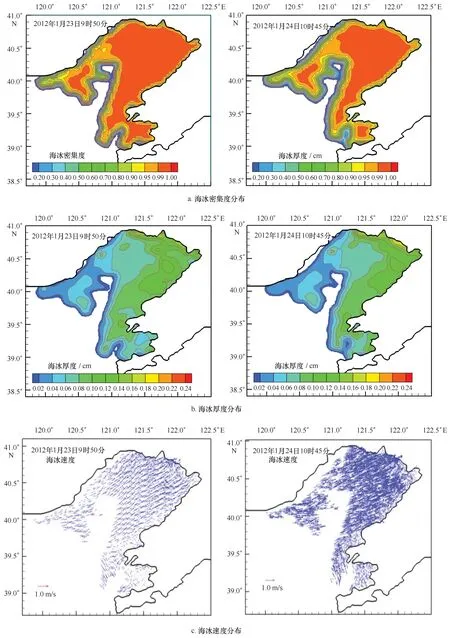
图10 MDEM模拟的海冰密集度、厚度和速度分布Fig.10 Distribution of ice concentration,thickness and velocity simulated with MDEM
4.2 辽东湾JZ20-2油气海域的海冰参数演化
在渤海海冰动力学模拟中,油气作业区海冰参数的确定对保障油气安全作业具有很强的工程意义,也是冰期油气作业中海冰管理工作的重要组成部分。在以上辽东湾海冰动力过程的改进离散元模拟中,可以对JZ20-2油气作业区(40°30′N,121°21′E)的海冰参数进行提取。这里采用SPH方法中的Gauss函数由该油气作业区的海冰单元插值得到该海域的海冰厚度、密集度、速度等参数。图11为JZ20-2油气作业区附近一个海冰单元的漂移轨迹,可以发现其受往复潮流和西北向风的拖曳作用,在往复运动过程中向西南方向漂移。图12和图13给出了该海域插值得到的海冰速度和厚度在48 h内的变化过程,实测值由该油气平台上的海冰现场监测及数字图像处理系统获得[45]。可以发现,海冰在半日潮作用下往复运动,其厚度保持相对稳定。结果表明,MDEM方法对该海域海冰参数的模拟结果与现场监测数值基本一致。
由于受海冰监测资料的限制,本文尚未对大风、寒流条件下的极端天气条件进行MDEM数值模拟。这在后续研究中将重点关注不同天气条件下的海冰动力演化规律,对海冰的重叠、堆积过程进行数值分析和实测数据验证,进一步检验MDEM方法对海冰动力过程的适用性。
5 结论
针对海冰的离散分布特点以及海冰漂移、重叠中的形变特征,本文发展了海冰动力过程的改进离散单元模型。它在拉格朗日坐标下将海冰离散为多个具有密集度、厚度的海冰单元,通过海冰单元间的摩擦、碰撞计算海冰内力。海冰单元间采用具有Mohr-Coulomb摩擦准则的黏弹性接触模型,并考虑海冰单元在法向力作用下的塑性变形。在海冰单元质量守恒条件下,计算单元相应的尺寸、密集度和厚度,由此获得海冰动力过程中的形变规律和重叠堆积特征。为验证该模型的可靠性,对变宽度水道内海冰的漂移和堆积过程进行了数值模拟,冰厚分布与解析值相吻合;通过对旋转风场内海冰漂移过程的数值分析,进一步验证了该模型对描述海冰动力学特性的精确性。最后,采用改进的离散单元模型对渤海海冰的动力过程进行了48 h数值模拟,计算结果与卫星遥感资料和油气作业区海冰现场监测数据相吻合。
海冰动力过程的改进离散单元模型具有物理意义明确、计算简单、精度高等优点,可对海冰在重叠堆积过程中产生的塑性变形进行有效的计算。在本文工作基础上将进一步考虑海冰的动力辐散现象,并针对热力因素的影响建立海冰单元的冻结和断裂模型,更好地应用于海冰的动力-热力过程的数值分析。

图11 辽东湾JZ20-2海域海冰单元漂移轨迹Fig.11 Drifting trajectory of one sea ice element at the JZ20-2 sea area of Liaodong Bay
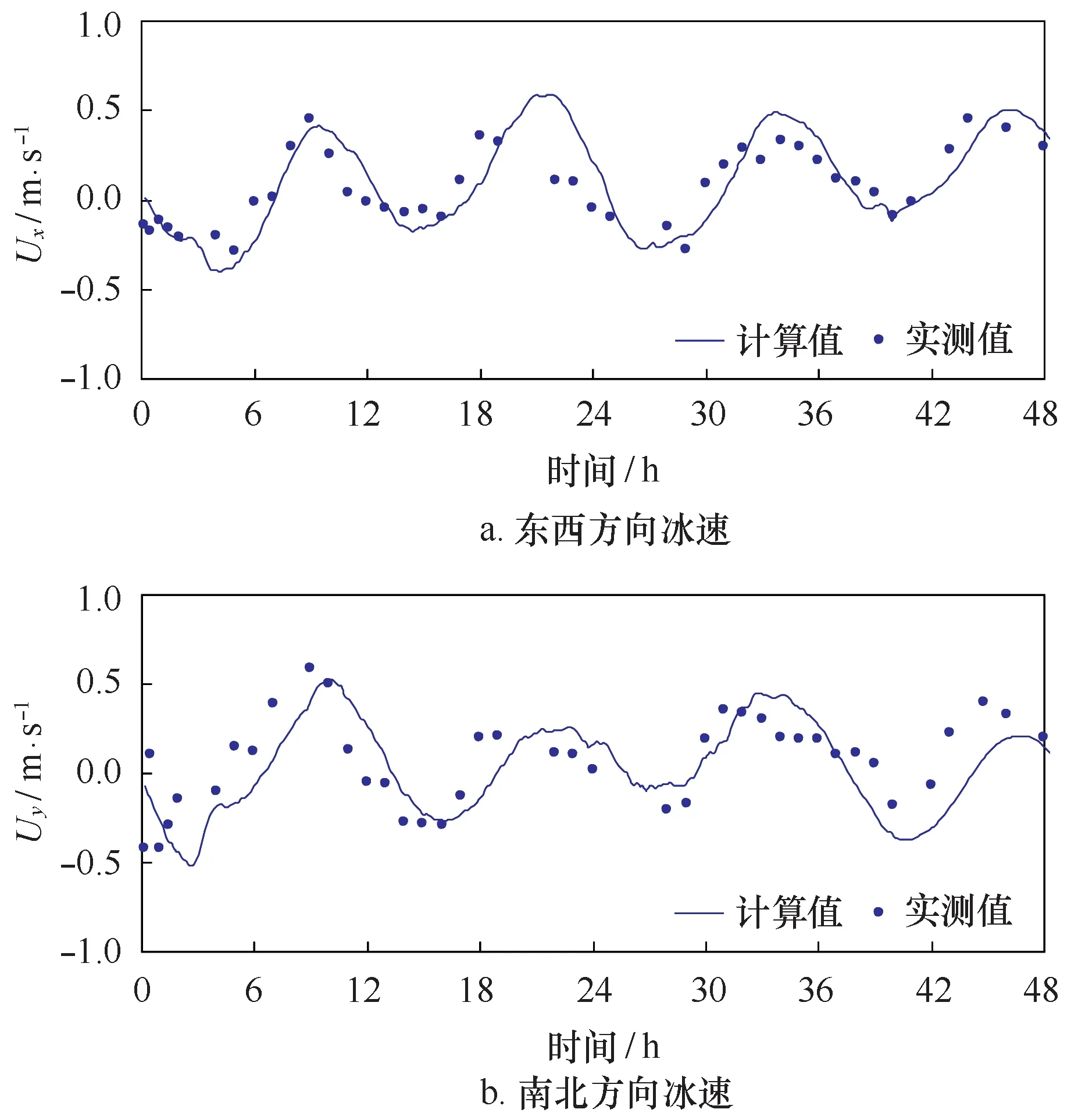
图12 辽东湾JZ20-2海域48 h模拟和实测冰速Fig.12 Simulated and measured ice velocity at the JZ20-2 sea area of Liaodong Bay for 48 hours
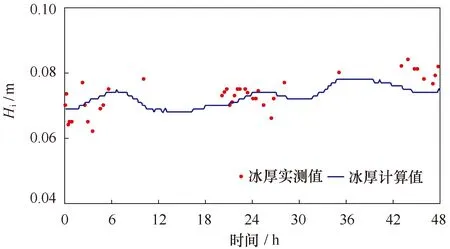
图13 JZ202海域48 h内的模拟和实测冰厚Fig.13 Simulated and measured ice thickness at the JZ20-2 sea area of Liaodong Bay for 48 hours
[1] 季顺迎,岳前进. 工程海冰数值模型及应用[M]. 北京:科学出版社,2011.
Ji Shunying,Yue Qianjin. Engineering Sea Ice Numerical Model and its Application[M]. Beijing: Science Press,2011.
[2] Holland M M,Stroeve J. Changing seasonal sea ice predictor relationships in a changing Arctic climate[J]. Geophysical Research Letters,2011,38: L18501.
[3] Dempsey J P. Research trends in ice model[J]. International Journal of Solids and Structures,2000,37(2): 131-153.
[4] Lepparanta M,Lensu M,Lu Q M. Shear flow of sea ice in the Marginal Ice Zone with collision theology[J]. Geophysica,1990,25(1/2):57-74.
[5] Tremblay L B,Mysak L A. Modeling sea ice as a granular material,including the dilatancy effect[J]. Journal of Physical Oceanography,1997,27(2): 2342-2360.
[6] OverLand J E,McNutt S L,Salo S,et al. Arctic sea ice sa a granular plastic[J]. Journal of Geophysical Research,1998,103(C10): 21845-21868.
[7] Hibler W D. Sea ice fracturing on the large scale[J]. Engineering Fracture Mechanics,2001,68(4): 2013-2043.
[8] Schulson E M. Compressive shear fault within arctic sea ice: Fracture on scale large and small[J]. Journal of Geophysical Research,2004,109(C07016): 1-23.
[9] Hibler W D. A Dynimic Thermodynamic sea ice model[J]. Journal of Geophysical Oceanography,1979,9(3):817-846.
[10] Zhang Z H,Lepparanta M. Modeling the influence of ice on sea level variations in the Baltic Sea[J]. Journal of Geophysical Research,1995,31(2): 31-45.
[11] 吴辉碇. 海冰的动力-热力过程的数学处理[J]. 海洋与湖沼,1991,20(4): 321-327.
Wu Huiding. Mathematic representations of sea ice dynamic thermodynamic processes[J]. Oceanologia et Limnologia Sinica,1991,20(4): 321-327.
[12] 苏洁,吴辉碇,白珊,等. 渤海冰-海洋耦合模式:Ⅱ.个例试验[J]. 海洋学报,2005,27(2): 18-27.
Su Jie,Wu Huiding,Bai Shan,et al. A coupled ice-ocean model for the Bohai Sea:Ⅱ. Case study[J]. Haiyang Xuebao,2005,27(2): 18-27.
[13] Gutfraind R,Savage S B. Smoothed Particle Hydrodynamics for the simulation of broken-ice field: Mohr-Coulomb-Type rheology and frictional boundary conditions[J]. Journal of Computational Physics,1997,134(3): 203-215.
[14] 季顺迎,沈洪道,王志联,等. 基于Mohr-Coulomb准则的黏弹塑性海冰动力学本构模型[J]. 海洋学报,2005,27(4): 19-30.
Ji Shunying,Shen Hongdao,Wang Zhilian,et al. A viscoelastic-plastic constitutive model with Mohr-Coulomb yielding criterion for sea ice dynamics[J]. Haiyang Xuebao,2005,27(4): 19-30.
[15] Flato G M. A particle-in-cell sea-ice model[J]. Atmosphere and Oceanography,1993,31(3): 339-358.
[16] Huang Z J,Savage S B.Particle-in-cell and finite difference approaches for the study of marginal ice zone problems[J]. Cold Regions Science and Technology,1998,28(1):1-28.
[17] 刘煜,吴辉碇,张占海,等. 基于质点-网格模式的海冰厚度变化过程数值模拟[J]. 海洋学报,2006,28(2): 14-21.
Liu Yu,Wu Huiding,Zhang Zhanhai,et al. Modeling for the dynamic process of ice thickness variation using a particle-in-cell ice model[J]. Haiyang Xuebao,2006,28(2): 14-21.
[18] Kubat I,Sayed M,Savage S,et al. Numerical simulations of ice thickness redistribution in the Gulf of St. Lawrence[J]. Cold Regions Science and Technology,2010,60(2): 15-28.
[19] Zhang J,Rothrock D A. Effect of sea ice rheology in numerical investigations of climate[J]. Journal of Geophysical Research,2005,110: C08014.
[20] Hutchings J K,Jasak H,Laxon S W. A strength implicit correction scheme for the viscous-plastic sea ice model[J]. Ocean Modelling,2004,7(2): 111-133.
[21] Wang L R,Ikeda M. A Lagrangian description of sea ice dynamics using the finite element method[J]. Ocean Modelling,2004,7(3): 21-38.
[22] Sulsky D,Schreyer H,Peterson K,et al. Using the material-point method to model sea ice dynamics[J]. Journal of Geophysical Research,2007,112: C02S90.
[23] 李海,季顺迎,沈洪道,等. 海冰动力学的混合拉格朗日-欧拉数值方法[J]. 海洋学报,2008,30(2):1-11.
Li Hai,Ji Shunying,Shen Hongdao,et al. A hybrid Lagrangian-Eulerian numerical model for sea ice dynamics[J]. Haiyang Xuebao,2008,30(2):1-11.
[24] Lemieux J F,Tremblay B,Sedlcek J,et al. Improving the numerical convergence of viscous-plastic sea ice models with the Jacobian-free Newton Krylov method[J]. Journal of Computational Physics,2010,229: 2840-2852.
[25] Tsamados M,Feltham D L,Wilchinsky A V. Impact of a new anisotropic rheology on simulations of Arctic sea ice[J]. Journal of Geophysical Research,2013,doi:10.1029/2012JC007990.
[26] Coon M D,Knoke G S,Echert D C,et al. The architecture of an anisotropic elastic-plastic sea ice mechanics constitutive law[J]. Journal of Geophysical research,1998,103(C10): 21915-21925.
[27] Hunk E C,Dukowicz J K. An elastic-viscous-plastic model for sea ice dynamics[J]. Journal of Physical Oceanography,1997,27(2): 1849-1867.
[28] Losch M,Danilov S. On solving the momentum equations of dynamic sea ice models with implicit solvers and the elastic-viscous-plastic technique[J]. Ocean Modelling,2012,41(4): 42-52.
[29] 王刚,岳前进,李海,等. 基于SPH方法的渤海海冰动力学数值模拟[J]. 大连理工大学学报,2007,47(3): 323-328.
Wang Gang,Yue Qianjin,Li Hai,et al. Numerical simulation of sea ice dynamics with Sph approach in Bohai Sea[J]. Journal of Dalian University of Technology,2007,47(3): 323-328.
[30] Liu M B,Liu G R. Smoothed Particle Hydrodynamics(SPH): an overview and recent developments[J]. Archives of Computational Methods in Engineering,2010,17(3):25-76.
[31] Dai M,Shen H H,Hopkins M A,et al. Wave rafting and the equilibrium pancake ice cover thickness[J]. Journal of Geophysical Research,2004,109: C07023.
[32] Herman A. Influence of ice concentration and floe-size distribution on cluster formation in sea-ice floes[J]. Central European Journal of Physics,2012,10(3): 715-722.
[33] Wilchinsky A V,Feltham D L. Rheology of discrete failure regimes of anisotropic sea ice[J]. Journal of Physical Oceanography,2012,42(4): 1065-1082.
[34] 季顺迎,李春花,刘煜. 海冰离散元模型的研究回顾及展望[J]. 极地研究,2012,24(4): 315-330.
Ji Shunying,Li Chunhua,Liu Yi. A review of advances in sea-ice discrete element models[J]. Chinese Journal of Polar Research,2012,24(4): 315-330.
[35] Rothrock D,Thomdike A S. Measuring the sea ice grian size distribution[J]. Journal of Geophysical Research,1984,89(C4):6477-6486.
[36] Shen H H,Hibler W D,Lepparanta M. On applying granular flow theory to a deforming broken ice field[J]. Acta Mechanics,1986,63(3): 143-160.
[37] Wichinsky A V,Feltham D L. Anisotropic model for granulated sea ice dynamics[J]. Journal of the Mechanics and Physics of Solids,2006,54(4):1147-1185.
[38] Sedlacek J,Lemieux J F,Mysak L A,et al. The granular sea ice model in spherical coordinates and its application to a global climate model[J]. Journal of Climate,2007,20(1):5946-5961.
[39] Hopkins M A,Frankenstein S,Thorndike A S. Formation of an aggregate scale in Arctic sea ice[J]. Journal of Geophysical Research,2004,109: C01032.
[40] Hopkins M A,Thorndike A S. Floe formation in Arctic sea ice[J]. Journal of Geophysical Research,2006,111: C11S23.
[41] Shen H T,Shen H H,Tsai S M. Dynamic transport of river ice[J]. Journal of Hydraulic research,1990,28(6): 659-671.
[42] Babic M,Shen H H,Shen H T. The stress tensor in granular shear flows of uniform,deformable disks at high solids concentrations[J]. Journal of Fluid Mechanics,1990,219(4): 81-118.
[43] Pariset E,Hausser R,Gagnon A. Formation of ice cover and ice jams in rivers[J]. Journal of Hydraulics Division,ASCE,1966,92(HY6):1-24.
[44] 沈洪道. 冰动力学的拉格朗日离散元模式[J]. 海洋预报,1999,16(3): 71-84.
Shen Hongdao. Lagrangian discrete-parcel model for ice dynamics[J].Marine Forecasts,1999,16(3): 71-84.
[45] 季顺迎,王安良,王宇新,等. 渤海海冰现场监测的数字图像技术及其应用[J]. 海洋学报,2011,33(4): 79-87.
Ji Shunying,Wang Anliang,Wang Yuxin,et al. A digital image technology and its application for the sea ice field observation in the Bohai Sea[J]. Haiyang Xuebao,2011,33(4): 79-87.
[46] Kwok R,Cunningham G F. ICES at over Arctic sea ice: Estimation of snow depth and ice thickness[J]. Journal of Geophysical Research,2008,113:C08010.
[47] Sun B,Wen J,He M,et al. Sea ice thickness measurement and its underside morphology analysis using radar penetration in the Arctic Ocean[J]. Science China,2003,46(11): 1151-1160.
Modified discrete element model for sea ice dynamics and its applications in the Bohai Sea
Ji Shunying1,Wang Anliang2,Mi Lili1,Liu Yu2,Li Baohui2
(1.StateKeyLaboratoryofStructuralAnalysisforIndustrialEquipment,DalianUniversityofTechnology,Dalian116023,China; 2.KeyLaboratoryofResearchonMarineHazardsForecasting,StateOceanicAdministration,NationalMarineEnvironmentalForecastingCenter,Beijing100081,China)
Breakup,rafting and ridging of ice cover exists widely in the polar and sub-polar regions. These processes affact the growth,vanishing and drifting of sea ice significantly. Considering the discrete distribution of sea ice on various scales,a discrete element model (DEM) should be developed to improve the sea ice numerical model and its computational precission. Thus,a modified discrete element model (MDEM) is established in this study to simulate the sea ice dynamics. Different with the traditional DEM,the ice cover is subdivided into a series of disks with their own characteristics including thickness,velocity,size and concentration,adopting the concept of smoothed particle hydrodynamics (SPH) of sea ice dynamics. Each sea ice element which is an assembly of ice floes changes in its size,concentration and thickness,according to the mass conservation law during drifting and inter-element collisions. According to the non-continuous distribution and rheology characteristics of ice cover,the viscous-elastic constitutive model is adopted. And the Mohr-Coulomb friction law is considered to determine the plastic deformation and tangential friction. To assess the reliability of this MDEM for sea ice dynamics,the drifting and ridging of ice cover in a various-width channel is simulated,and the simulated distribution of ice thickness is validated by the analytical solution. The drifting of sea ice in a rotational wind field is also simulated efficiently with high precision. Moreover,the sea ice dynamics in the Bohai Sea is simulated for 48 h. The simulated results match well with the satellite remote images and field observed data. In the future study,the MDEM will be improved by coupling dynamics and thermodynamics of sea ice. The growth,vanishing and drifting of sea ice will be simulated more accurately by consideringthe refrozen effect and breakage feature of ice cover.
sea ice dynamics; discrete element model; ice ridge; Bohai Sea
10.3969/j.issn.0253-4193.2015.05.006
2013-04-28;
2015-01-11。
国家自然科学基金项目(41176012);国家海洋公益性行业科研专项经费项目(201105016, 201205007);高等学校博士学科点专项科研基金项目(20130041110010)。
季顺迎(1972年—),男,河北省武邑县人,博士,教授,从事工程海冰数值模型研究。E-mail:jisy@dlut.edu.cn
P731.15
A
0253-4193(2015)05-0054-14
季顺迎,王安良,米丽丽,等. 海冰动力过程的改进离散元模型及在渤海的应用[J]. 海洋学报,2015,37(5):54-67,
Ji Shunying,Wang Anliang,Mi Lili,et al.Modified discrete element model for sea ice dynamics and its applications in the Bohai Sea[J]. Haiyang Xuebao,2015,37(5):54-67,doi:10.3969/j.issn.0253-4193.2015.05.006
