复合层合梁层裂损伤与超声导波的相互作用研究

许伯强,来 锴,徐桂东,徐晨光

(江苏大学 理学院,江苏 镇江 212013)

复合层合梁层裂损伤与超声导波的相互作用研究

许伯强,来 锴,徐桂东,徐晨光

(江苏大学 理学院,江苏 镇江 212013)

基于谱有限元法(SFEM),建立了压电晶片驱动/传感与各向异性层状复合梁耦合的谱有限元模型,数值模拟研究了耦合系统超声导波的激发、传播特征,并分析了导波与损伤的相互作用。模型中复合梁采用铁木辛柯梁理论、压电晶片层采用欧拉伯努利梁理论,利用哈密顿原理得到梁/压电晶片的时域耦合运动控制方程和边界条件,通过快速傅里叶变换将耦合运动控制方程转换至频域可导出谱有限元模型。与有限元分析结果比较表明,所建模型可精确模拟复合梁中导波的传播且计算效率高。进而分析了导波和层裂损伤的相互作用,结果表明导波在缺陷处会产生反射,且反射信号到达压电传感器的时间和幅值与缺陷的位置及长度有关。

复合材料层合梁;层裂损伤;谱有限元模型;压电晶片驱动/传感

复合材料由于比强度和比模量高等固有优势已在航空航天、汽车、机械制造等领域得到广泛应用[1]。在机械荷载、环境温度变化等因素作用下,复合材料易产生脱层损伤,其降低了材料的压缩强度和刚度,严重时可能引起材料失效,以致酿成灾难性事故。因此,为了确保复合材料结构的可靠性和安全性,对其进行脱层损伤监测尤为重要。

超声导波具有传播距离长、能量损失小,对构件内部微小损伤敏感等优点,已被用于各种不同材料构件的损伤检测[2]。基于压电效应的压电晶片因其易于操控、廉价等特点已成为一种新型的超声换能器。由于超声导波在损伤复合构件中传播的复杂性,建立压电晶片与结构的耦合动力学响应数值模型,构建快速、有效的损伤算法,将有助于压电晶片在结构损伤监测中的应用。诸多数值方法如有限元法(FEM)[3]和“频域”谱元法[4]已被用于对导波传播的数值分析。Xu等人提出了一种超声导波在各向同性/各向异性的薄膜/衬底材料中的FEM模型[5]。Pesin和Pustovoytov利用有限元法对热轧板的表面裂纹到边缘缺陷的转变进行了研究和模拟分析[6]。有限元法求解高频超声导波的问题时,因导波波长较短,需要对求解域划分更精细的网格,且为了避免梁结构边界处导波的反射,通常会考虑增加模型的几何尺寸,这将极大了增加模型的计算资源[7]。Doyle首次提出谱有限元法(SFEM)研究结构中超声导波的传播[8]。该方法结合了有限元法的灵活性和谱分析快速的优势,仅用少量单元就能得到控制方程的高精度解、且运算速度快。Lee和Kim[9]首先基于伯努利梁理论建立了各向同性梁和压电片耦合的双层复合梁的谱元模型。后来,Park等[10]又基于铁木辛柯梁理论发展了这一模型。然而,由于复合梁的各向异性的特性,需进一步发展基于铁木辛柯梁理论的各向异性梁和压电片耦合的谱元模型。

1 控制方程

1.1 耦合复合梁的运动假设

如图1所示,压电复合梁是由复合基梁和压电晶片构成。坐标系(x,y,z)为复合梁的全局坐标系。基梁是由多层各向异性的复合材料层铺叠而成,基梁铺层的主坐标系(1,2,3)是以相对于x轴转过一任意角φ确定的。

图1 复合梁的几何尺寸和坐标

基于铁木辛柯梁理论和欧拉伯努利梁理论,复合梁和压电晶片的位移场定义为

(1)

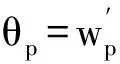
(2)

在电压激励下,仅考虑压电晶片做轴向振动,则相应的压电本构关系定义为

1.2 控制方程和边界条件

依据参考文献[12]可得复合梁的总动能T,总应变能V和总虚功δW分别为

(4)

其中,fu、fw和fθ是沿x轴分布的外部载荷;N、V和M是施加于边界x=0和l处的轴向力,横向剪切力和弯矩。

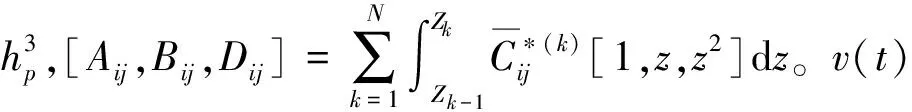
(5)

力的边界条件

(6)

电位移

(7)

2 谱元模型

2.1 耦合复合梁单元的谱元模型

通过快速傅里叶变换将运动方程和边界条件转换至频域。基梁中性轴上响应量和电压的谱形式为

Wn(x),Φb(x),Vn}eiωnt

(8)

将以上谱形式代入边界条件和控制方程可得到波数k和波模比r。通过频域控制方程和边界条件构造形函数矩阵和力矩矩阵,采用矩阵缩减方法可得到复合梁单元的谱元方程[10]

K(ω)d=f

(9)

式中,d是单元的节点位移向量;f是单元的节点力向量;K(ω)是单元的动态刚度矩阵。

2.2 脱层复合梁单元的谱元模型

如图2(a)所示的复合梁内含脱层,脱层贯穿宽度方向。假设脱层面的上下子层之间无接触,各界面处的横截面都是直的。文献[13]提出将4个单元如图2(b)所示的谱有限元元方程组装,得到脱层复合梁单元的谱有限元模型。根据节点3～5,6～8的位移关系、左界面AB和右界面CD的力平衡,可将4个单元的谱有限元方程写为

(10)

图2 脱层复合梁的建模

缩合节点4和7的自由度,可得到最终的平衡方程形式

(11)

3 数值结果和讨论

图3 悬臂对称层叠复合梁

3.1 压电晶片层对色散曲线的影响

图4显示了表面完全黏合压电晶片层和无压电晶片的[0/90/90/0]s对称层叠复合梁的色散曲线。图4结果表明:(1)在基梁中有3种波模式S0、A0和A1(分别表示轴向波,弯曲波,剪切波),只有信号频率超过截止频率才会出现A1波传播模态,当低于截止频率时剪切波为耗散模态。(2)压电晶片层的存在使波数k在同频率下变大,这是由于压电晶片层的存在改变了复合梁单元的厚度。且与无压电晶片层的情况相比,截止频率由于压电晶片层而降低。(3)当信号频率低于截止频率时,A1波的群速度为零,即此时仅存在A0波和S0波这两种传播波模态。

图4 压电晶片对[0/90/90/0]s对称复合梁色散曲线的影响

3.2 复合材料叠层的铺层角度的影响

图5展示了4个不同铺层角度[α/90/90/α]s对称复合梁A0波的色散和群速度曲线。很显然,随着波数铺层旋转角度α从0°增加到60°,在考察频率范围内,波数逐渐增加且A0波的群速度逐渐降低。这表明铺层角度α显著影响了基梁中波的传播特性。另外,随着角度α的增加,A0波的波数和群速度的变化量逐渐变小。

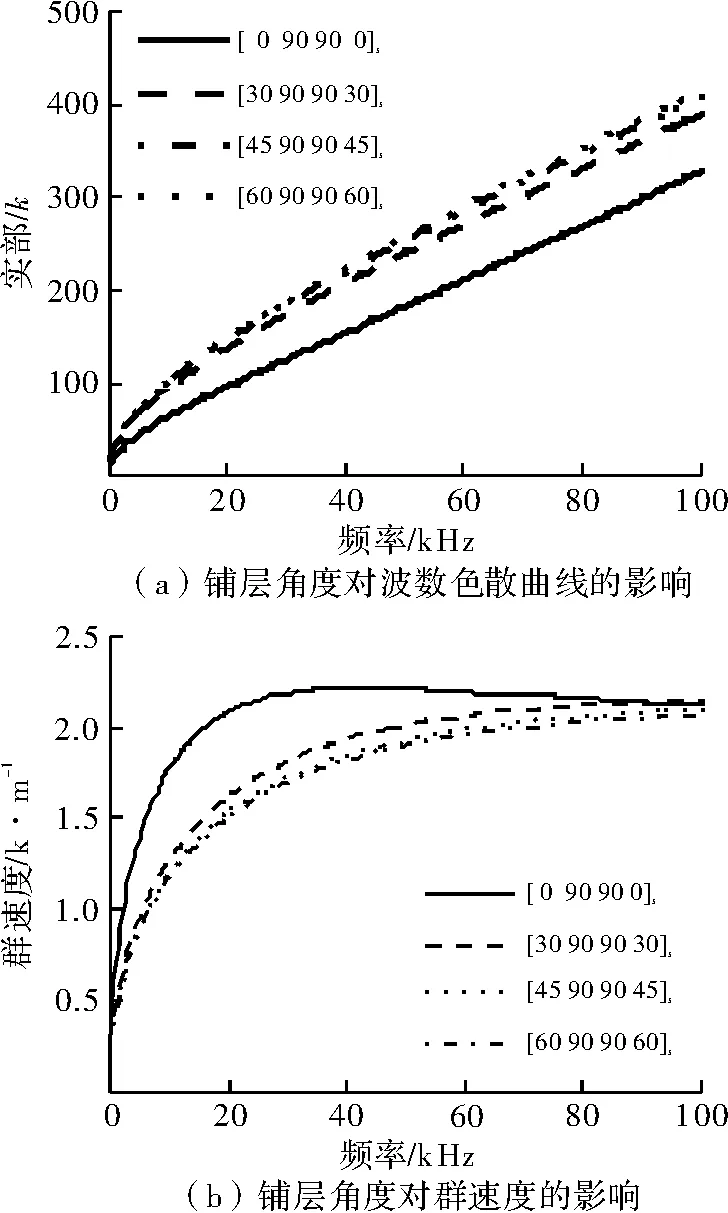
图5 对称复合梁铺层对弯曲波波数和群速度的影响

3.3 复合梁中的导波

本研究中的悬臂复合梁的铺层角度排列顺序为[0/90/90/0]s,如图3(a)所示。该数值分析中的几何参数是l1=2 000mm,l2=500mm,l3=1 000mm。激励信号为汉宁窗函数调制的五峰正弦电压信号,电压峰峰值是200V,中心频率为70kHz。图6比较了SFEM和FEM得到的传感信号。对于相同复合梁动态响应的检测,SFEM模型仅需5个单元,FEM模型需93 397个单元,这使得SFEM的计算时间需要大约5min,而FEM的计算时间却需要8h。图6表明两种方法得到的归一化电压基本一致,表明了本谱有限元模型的高效性和准确性,图中两条曲线的小差别是由于两种方法的运动假设不同。图7展示的是无损梁和脱层梁上传感器接收到的信号,模型如图3(b)所示,l1=1 000mm,l2=500mm,l3=500mm,l4=500mm。图中可看出,与无损梁相比,含脱层缺陷梁中的波多了一个来自该缺陷的反射波,这是由于缺陷的声阻抗与材料的声阻抗不同,波在缺陷处被反射而出现缺陷波信号。

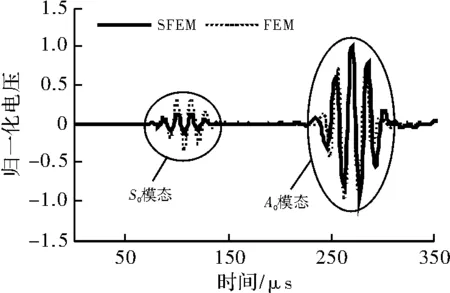
图6 谱有限元法和有限元法结果的比较

图7 无损梁和脱层梁的比较电压信号(脱层位于4、5层之间)

3.4 脱层对导波的影响

为探究脱层位置和长度对复合梁动态特性的影响,考虑如图3(b)所示的复合梁,脱层位于基梁的中平面上。图8(a)展示了几何参数为l1=1 000mm,l2=500mm,l3=500mm,l4=500mm的复合梁的动态响应。考虑了3个脱层长度(ld=20,50,80mm)。由图8(a)可观察到一个来自脱层的反射波,反射波位于入射波和来自左边界的反射波之间,且随着脱层长度的增加,反射波的幅值也变大。图8(b)展示了无损复合梁和脱层(ld=50mm)复合梁的传感电压。很明显,图中位于入射波和边界反射波之间的第一个小波包是l3=300mm时脱层的反射波,第二个小波包是在l3=500mm时脱层的反射波,这说明脱层距激励器越远,脱层反射波信号到达的时间就越晚。根据图示导波传播特征,文中可直接利用波速和缺陷波信号到达的时间得到脱层的位置。

图8 脱层对电压信号的作用

4 结束语

本文基于谱有限元方法,建立了各向异性层状复合梁和压电晶片耦合,以及包含脱层复合梁单元的谱有限元模型,研究了压电复合梁中导波传播特性及导波与脱层缺陷的相互作用。与传统有限元分析结果比较,证实了该谱有限元模型的高效和精确性。数值模拟得到复合梁在不同层叠角度及有无压电晶片时的导波传播色散曲线,脱层缺陷位置和长度变化时接收的导波信号,结果表明:复合梁的层叠角度会导致导波传播色散特性的改变;压电晶片的存在使波的色散更明显,尤其是在高频;导波在脱层缺陷处会产生反射,并且反射信号到达压电传感器的时间和幅值与缺陷的位置及长度有关。根据缺陷波到达的时间、波速和缺陷波的幅值,可对脱层缺陷进行准确定位及损伤程度判断。本文建立的谱有限元模型显示了其对损伤复合梁脱层位置的评价能力,相关结果为实验研究提供了分析基础。

[1]ReddyJN.Mechanicsoflaminatedcompositeplates:theoryandanalysis[M].NewYork:CRCPress,1997.

[2] 李红.超声导波在粘弹性介质中传播与能量衰减的特性研究[D].镇江:江苏大学,2011.

[3]WuF,ChangFK.Debonddetectionusingembeddedpiezoelectricelementsforreinforcedconcretestructures-partII:analysisandalgorithm[J].StructuralHealthMonitoring,2006,5(1):17-28.

[4]PengH,YeL,MengG,etal.ConciseanalysisofwavepropagationusingthespectralelementmethodandidentificationofdelaminationinCF/EPcompositebeams[J].SmartMaterialsandStructures,2010,19(8):11-14.

[5]LuoYing,LiHong,XuBaiqiang.Spectralfiniteelementmethodmodelingofultrasonicguidedwavespropagationinlayeredviscoelasticfilm/substratematerials[J].JournalofAppliedPhysics,2010,108(12):123505-123512.

[6]PesinA,PustovoytovD.Researchofedgedefectformationinplaterollingbyfiniteelementmethod[J].JournalofMaterialsProcessingTechnology,2015,220(6):96-106.

[7] 许伯强,刘洪凯,徐桂东,等.基于应力-位移混合有限元法的激光超声数值模拟[J].激光技术,2014,38(2):230-235.

[8]DoyleJF.Wavepropagationinstructures:spectralanalysisusingfastdiscretefouriertransforms[M].NewYork:Spring-Verlag,1997.

[9]LeeU,KimJ.Dynamicsofelastic-piezoelectrictwo-layerbeamsusingspectralelementmethod[J].InternationalJournalofSolidsandStructures,2000,37(32):4403-4417.

[10]ParkHW,KimEJ,LimKL,etal.Spectralelementformulationfordynamicanalysisofacoupledpiezoelectricwaferandbeamsystem[J].ComputersandStructures,2010,88(9-10):567-580.

[11]陈建桥.复合材料力学概论[M].北京:科学出版社,2006.

[12]WangG.Analysisofbimorphpiezoelectricbeamenergyharvestersusingtimoshenkoandeuler-bernoullibeamtheory[J].JournalofIntelligentMaterialSystemsandStructures,2013,24(2):226-239.

[13]SrinivasanG,MassimoR,SathyanarayaH.Computationaltechniquesforstructuralhealthmonitoring[M].Heidelberg:SpringerLondonLtd,2011.

[14]MahapatraD,GopalakrishnanS.Aspectralfiniteelementforanalysisofwavepropagationinuniformcompositetubes[J].JournalofSoundandVibration,2003,268(3):429-463.

[15]JaffeH,BerlincourtDA.Piezoelectrictransducermaterials[J].ProceedingsoftheIEEE,1965,53(10):1372-1386.

Study of Interactions Between Delamination Damage in a LaminatedComposite Beam and Ultrasonic Guided Wave

XU Boqiang,LAI Kai,XU Guidong,XU Chenguang

(School of Science,Jiangsu University,Zhenjiang 212013,China)

Based on the spectral finite element method(SFEM),a spectral finite element model is developed for a delaminated laminated composite beam coupled with a surface-bonded piezoelectric actuator/sensor.Ultrasonic guided wave excitation and propagation characteristics of the coupling system are researched by numerical simulation,and the interactions between the guided wave and the defect are analyzed.The composite beam is based on the Timoshenko beam theory and the piezoelectric wafer layer is represented by the Euler Bernoulli beam theory in the model.The beam/piezoelectric wafer coupled governing motion equations and the boundary conditions in time domain are obtained by using the Hamilton’s principle,and then the spectral finite element model is formulated by transforming the coupled governing equations into frequency domain via the discrete Fourier transform.The high calculation efficiency and the ability of the present model to accurately predict the wave propagation in the composite beam are verified by comparing with the finite element method results.Then the interactions between the waves and the damage are discussed.The results show that the guided wave can generate reflection wave from the defect,and that the arrival time and the amplitude of the reflection wave are related to the location and the length of the defect.

laminated composite beam;delamination damage;spectral element method;piezoelectric actuator/sensor

2015- 03- 30

国家自然科学基金资助项目(11172114);江苏省六大人才高峰基金资助项目(2012-ZBZZ-027)

许伯强(1963—),男,博士,教授,博士生导师。研究方向:超声无损检测与评价,先进传感器设计。E-mail:bqxu@mail.ujs.edu.cn。来锴(1989—),女,硕士研究生。研究方向:复合材料损伤检测。

10.16180/j.cnki.issn1007-7820.2015.11.015

TN04;O422

A

1007-7820(2015)11-055-06