基于有限元的冷床格栅裂纹热力耦合分析与优化

宋则进 金沙沙

(中冶京诚工程技术有限公司 北京100176)

基于有限元的冷床格栅裂纹热力耦合分析与优化

宋则进①金沙沙

(中冶京诚工程技术有限公司 北京100176)

针对中厚板冷床设备在生产中产生的裂纹缺陷，分析拉裂纹的产生原因。展开了设计改进，采用有限元软件等方法进行分析，对冷床格栅进行了应力与变形分析，找到了开裂的原因，并且通过控制该机设备结构，优化设计，选择合适的材料，解决此类问题。

冷床格栅 有限元 裂纹 热力耦合分析

1 引言

步进式冷床是热轧中厚板冷却的主要设备，用于冷却轧制后的钢板。中厚板热矫后温度为 500℃～900℃，要求均匀迅速冷却至 100℃～150℃以下，在冷却钢板的同时将钢板移送至下一道工序，并保证钢板在冷却过程中的平直度、尽可能避免钢板下表面产生划伤。因此冷床在精整区起到十分重要的作用，近十多年来得到广泛应用。步进式冷床是一种大型结构冷床，它由上下料装置和具有良好的平面性的多组固定梁及格栅、活动梁及格栅组成。活动梁及格栅可通过液压或电动升降传动装置及移送传动机构使其上下及前后运动，达到冷却和输送钢板的目的。通常的步进冷床分为常规型和特厚板型。国内某钢厂是一条5000mm中厚板生产线，设备投产后该线上的特厚板冷床固定梁格栅上出现横向裂纹，钢厂对裂纹的出现没有良好的对策，现场维修效果不佳(如图1)通过焊接修补裂纹，但没有成功，裂纹继续扩大，因此通常的方法是更换格栅梁，这些格栅的出现，不但影响冷床的正常运行，而且也导致了很大的经济损失。通过对格栅裂纹这种缺陷进行分析、研究，制定一系列的措施，来解决这一问题。提高生产效率，减少经济损失。对于冷床这种工况温度高、载荷大的设备，传统的单一强度校核已经无法满足要求，需要通过有限元法来研究应力与变形，指导设计。

图1 冷床格栅裂纹

2 固定梁格栅有限元模型的建立

2.1 固定梁格栅结构

原格栅梁是一个网格式的空间结构，由纵梁、横梁组成，纵梁起承载作用。承受的载荷主要由纵梁承担，且纵梁工作温度高、上下表面温差大，纵梁的寿命决定了格栅的寿命。固定梁格栅为整体式结构，原格栅的三维模型见图2，通过结构优化，修改后的结构见图3。降低格栅热流密度较高处高度，增加格栅厚度，增加间距。

图2 原格栅的三维模型图

图3 修改后格栅的三维模型图

2.2 有限元模型与网格划分

采用自动划分的方法获得的网格，由于没有指定网格划分方法和大小，单元畸变度达到了0.99。复杂几何区域的网格单元会变扭曲。劣质的单元会导致劣质的结果，或者在某些情况无结果，有很多方法来检查单元网格质量 (mesh metrics)。例如 ，一个重要的度量是单元畸变度( Skewness )。畸变度是单元相对其理想形状的相对扭曲的度量，是一个值在0 (极好的) 到1 (无法接受的)之间的比例因子。

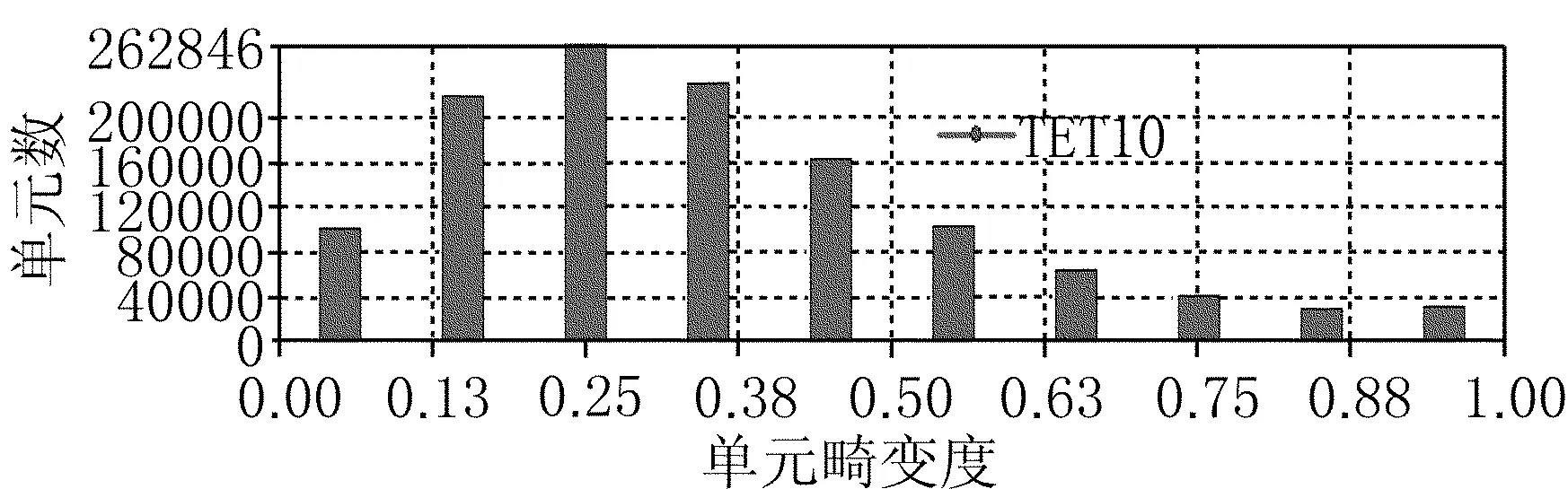
图4 平均单元网格质量(mesh metrics)

在ANSYS中应用以下原理划分网格：利用四面体单元(Tetrahedrons)划分实体，相关度中心定义为fine：relevance和element值定义为100和0.01采用自Solidedge导入的建模方法，建立实体模型，保存成iges格式后，导入ANSYS进行有限元分析。充分利用三维设计软件建模方便和易于修改的特点，简化了建立三维有限元模型的繁琐过程。整个模型共划分为1974848个单元，1204562个节点。

表1 不同温度下导热系数

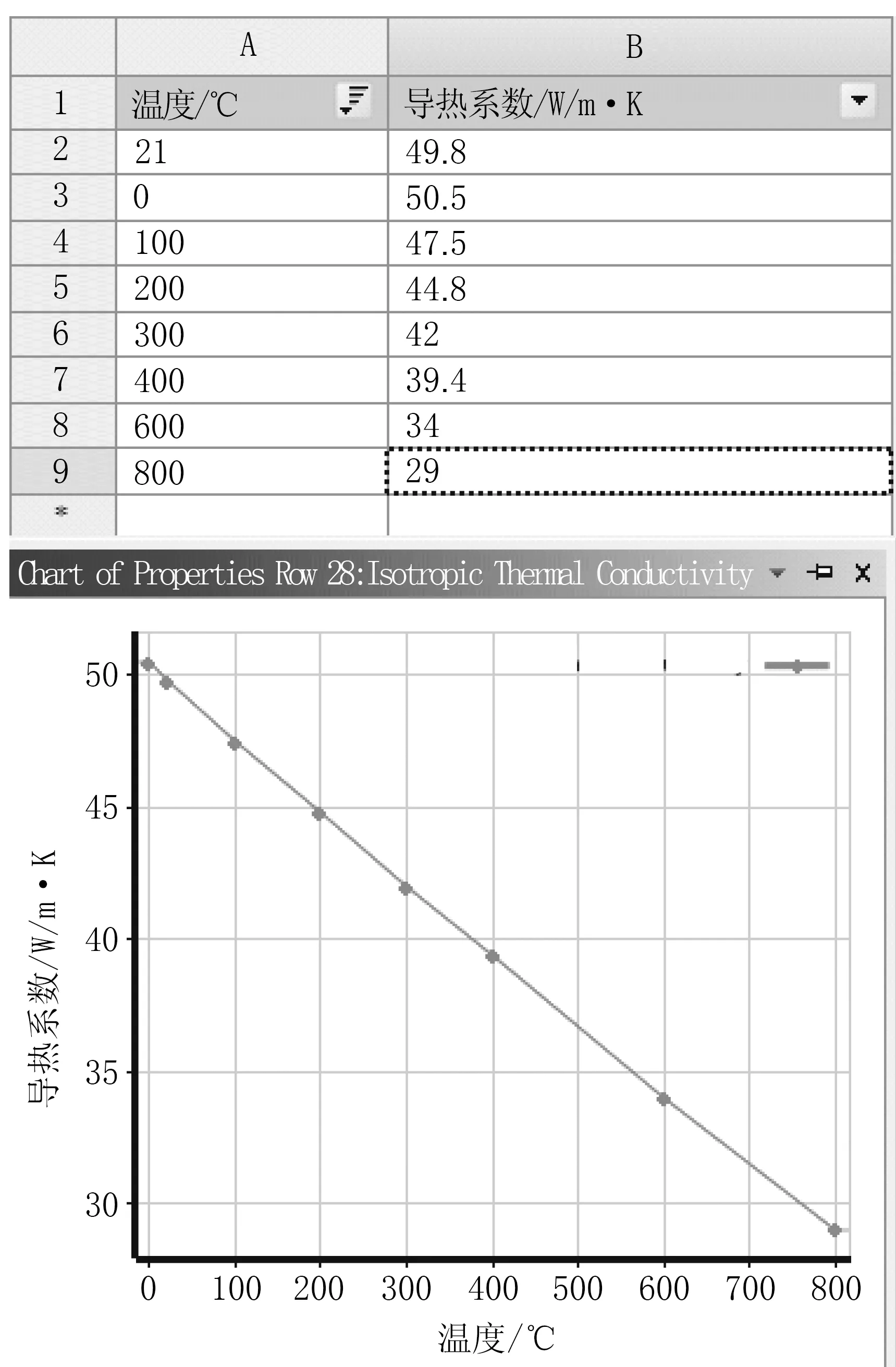
图5 线膨胀系数曲线

单元畸变度降低到了0.34可以接受的程度。

2.3 材料特性参数确定

格栅材料为铸造碳钢QT230-450，修改后的格栅材料为铸造碳钢QT310-570，特性参数如下：

弹性模量：见曲线图6

泊松比：0.30

屈服极限：310MPa

抗拉强度：570MPa

密度：7850kg/m3

导热系数：见曲线

线膨胀系数：见曲线图5

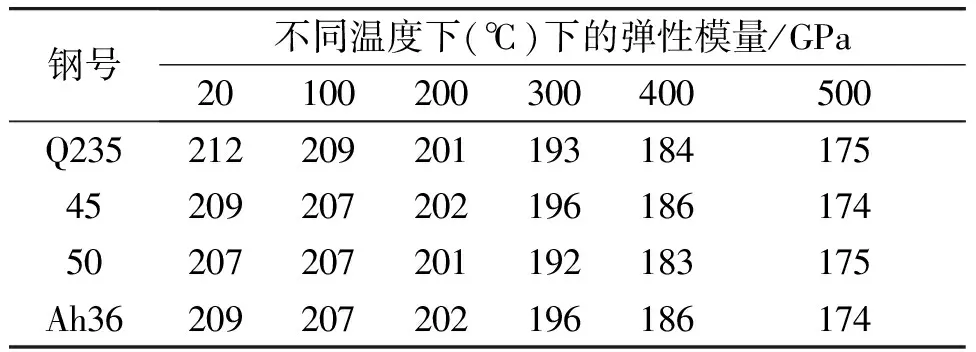
表2 不同温度下弹性模量

表3

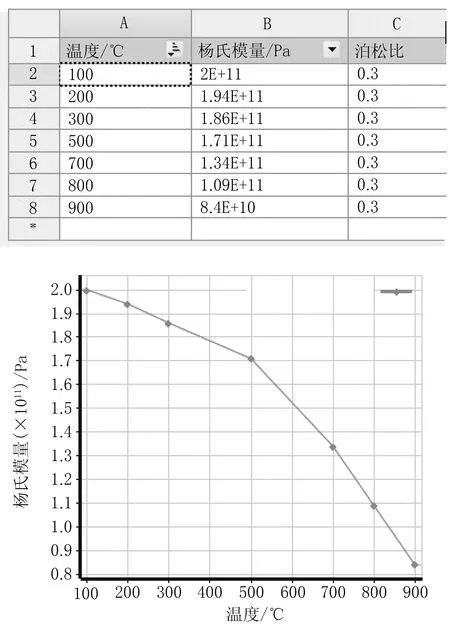
图6 弹性模量系数曲线

通过分析比较不同温度对α-Fe弹性模量的数据，在一定温度区间回归得到α-Fe的弹性模量E的近似关系式(1)(2)，得到表2和图6弹性模量系数曲线：

Eα-Fe=230660-76.665(T+273)(20℃-583℃)

(1)

Eα-Fe=385350-257.41(T+273)(583℃-911℃)

(2)

3 冷床热分析数学模型程

一般而言，热分析可分为稳态热分析和瞬态热分析两种。其中，温度场随时间而变化的传热过程称为瞬态传热，反之则为稳态传热。在进行瞬态热分析以前，通常需要通过稳态热分析来确定初始温度分布；而对于一个从瞬态逐渐过渡到稳态的传热问题，则将稳态热分析作为瞬态热分析的最后一部工作，用以确定系统在稳态时所处的状态。根据能量守恒原理，上述两种情况的热平衡方程可以统一表达为公式(3)：

(3)

式中 A—热扩散率，m2/s； λ—导热系数，W/m·K; qv—内热源强度，W/m。

热分析过程是指对一个系统在加热或是冷却过程中其热场分布状态及其变化规律的分析和描述。分析的方法分为实验分析法．数值解析法和计算法共三种。

其中，数值解析法以数学为基础求解定解问题，得出的解用函数形式表达。虽然此法求得的解精确可靠，但通常只能用于有规则边界条件的问题；实验法是利用热像仪等分析仪器进行测试分析的方法，其操作简单，缺点是只能获得被测对象的表面温度，并且要求必须有被测实物等；数值计算法是一种以离散数学为基础的求解方法，常见的是有限元法和有限差分法。此法求解精度高，适宜于解算复杂模型，是当前广泛应用的一种方法。

综合分析冷床工作，可以按稳态进行热分析，热场可以用偏微分方程描述。在各种热场问题的模型及其数值解的方法中，有限元分析法特别适合解决具有复杂边界的偏微分方程及求解过程的向量化。这时，可以把热平衡方程用矩阵形式表达为：

(4)

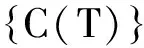
物体的材料参数等不随温度的变化而变化，即二者分别为K和C时，式(4)即为系统稳态热分析表达式。

4 ANSYS有限元计算结果

4.1 边界条件

设置格栅梁两端在Y,Z方向的位移为零，X方向自由，载荷均布在格栅梁顶面-Z方向。格栅梁的载荷分3种情况考虑:①只考虑机械载荷作用;②只考虑温度载荷作用;③考虑机械载荷与温度载荷的共同作用。当温度900℃的钢板长时间停留在冷床上的时候，格栅梁的温度最高、上下表面温差最大，且承担的机械载荷为循环周期内的最大载荷，将格栅梁的机械载荷与温度载荷作为本次分析的载荷条件。

铸造碳钢QT310-570的抗拉强度为570MPa，取安全系数为1.5，则许用应力为:380MPa。

4.2 机械载荷单独作用时的格栅梁强度分析

在格栅梁两端分别施加约束：UY-0，UZ-0，在格栅梁顶面的-Z方向施加最大面载荷25KN，并施加重力。由应力云图与位移云图可以看出，虽然格栅梁中部应力值较大，但最大应力为6.5MPa；其余部分的应力值较小，在1.0～3.0MPa之间。因此，在机械载荷单独作用下，格栅梁完全能满足刚度要求。而且如果是机械载荷产生的裂纹，应该在格栅梁下部，这与现场实际情况不符，所以机械应力并不是设备裂纹的主要原因。

4.3 温度载荷单独作用时的格栅梁热应力分析

采用间接法进行温度载荷单独作用时的热应力分析，先对格栅梁进行稳态热分析，在格栅梁的顶面施加900℃的温度载荷和其他表面施加30℃的环境传导温度，可得到格栅梁的温度云图如图9所示。在格栅梁两端施加约束，读入热分析结果并将其作为载荷。得到格栅梁位移云图、主应力云图见图10。

由格栅梁的温度云图可知，在同一高度方向上温度相同，在横截面上自顶至底温度呈线性降低，顶面温度最高，底面温度最低，格栅交联处的温度及热通量最高，这与给定温度条件是一致的。

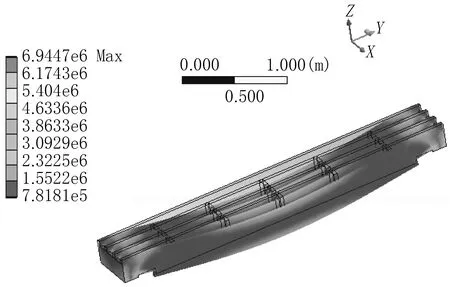
图7 格栅梁主应力云图(只有机械载荷)

图8 格栅梁位移云图(只有机械载荷)

图9 格栅梁的温度云图

由格栅梁Y分量位移云图可知，由于热应力的结果，格栅梁顶的中间部分位移最大，呈扇形向上。因此，在温度载荷单独作用下，应力值已经达到280MPa，可见温度是格栅梁主要应力源。

由格栅梁主应力云图可得:在温度载荷单独作用下，格栅梁完全能满足强度要求。

图10 格栅梁的主应力云图(只有温度载荷)

图11 格栅梁主应力云图(机械载荷与温度载荷共同作用时)

图12 格栅梁位移云图(机械载荷与应力载荷共同作用时)

4.4 机械载荷与温度载荷联合作用时的梁热应力分析

采用间接法进行机械载荷与温度载荷联合作用时的热应力分析，先对格栅梁进行稳态热分析，在格栅梁的顶面施加温度载荷及面载荷，并施加重力，读入热分析结果并将其作为载荷。求解后得到格栅梁位移云图见图12，格栅梁主应力云图见图11。由格栅梁位移云图可知，在温度载荷与机械载荷的联合作用下，不考虑建模产生的压力集中部位，在最大弯曲变形处的最大应力为290MPa左右，格栅梁底部的中间段向上弯曲，最大向上弯曲量在该区域，这也与现场裂纹出现的位置相一致，因此，在温度载荷与机械载荷联合作用下，新设计的格栅梁完全能满足刚度要求。

5 结论

1)通过优化设计改进方案，在没有增加设备重量，投资的情况下，可以采取渐变式的壁厚过渡形式、格栅梁连接处设计过渡圆角、增加壁厚、增加材料强度等措施降低该部分的主拉应力。

2)在格栅梁表面格栅交叉处存在严重应力集中现象，应力集中、裂纹与载荷是格栅梁开裂的主要原因。针对格栅梁交叉处的应力集中现象，格栅梁受到机械载荷与温度载荷的共同作用，温度载荷是影响格栅梁应力分布与变形的首要因素。

3)降低格栅梁的温度是减小格栅梁热应力的最直接、最有效的措施，冷床作为运动的过渡的钢板运输设备，应避免厚板长时期停留在冷床上，至少应该原地踏步，以减少向格栅梁的传热。

4)关于宝钢现场出现的另一种格栅梁向下方“塌腰”的问题，从格栅梁的应力与变形来看，在正常铸造工艺与烧结生产情况下，不可能“塌腰”，“塌腰”另有它因。可能是由于生产不正常导致格栅梁温度过高，从而造成蠕变失效;也可能是铸造工艺、成分控制等不符合要求所致，具体原因还有待进一步研究。

[1]左晓明.基于ANSYS的生物质餐具成型模具热分析及优化[J].机械设计与制造,2010(12).

[2]陈耀武,赵良知,黄锦强.基于Pro/E与ANSYS的一模多腔模具热分析[J].模具技术,2007(6).

[3]李春玲.柴油机气缸盖温度场数值模拟[J].柴油机设计与制造,2006(2).

[4]曾智灵,任立军.基于ANSYS的连铸机拉矫辊热结构耦合分析[J].重型机械,2008(2).

Thermal Coupling Analysis and Optimization on Cooling Bed Grille Crack Based on Finite Element

Song Zejin Jin Shasha

(Capital Engineering and Research Incorporation Limited, Beijing 100176)

According to the crack defect of cooling bed in the production, analysis the causes of crack. By using finite element software, the stress and deformation analysis of cooling bed grille, found the causes of cracking, and through the control of the equipment structure, optimization design, selection of appropriate materials, to solve the problem.

Cooling bed grille Finite element Crack Thermal coupling analysis

宋则进，男，1978年出生，2006年毕业于东北大学研究生院机械工程系机械设计理论专业，硕士研究生，高级工程师，从事冶金机械设备方面的研发及设计工作

TG333.3

A

10.3969/j.issn.1001-1269.2015.02.005

2014-07-22)