2种改进的PWM方法及其在径流区间估计中的应用
2015-06-24袁永生戴启璠
康 慧,袁永生,戴启璠
(1.河海大学 理学院,江苏 南京 210098; 2.江苏省灌溉总渠管理处,江苏 淮安 223200)
2种改进的PWM方法及其在径流区间估计中的应用
康 慧1,袁永生1,戴启璠2
(1.河海大学 理学院,江苏 南京 210098; 2.江苏省灌溉总渠管理处,江苏 淮安 223200)
对于小样本的时间序列应用2种改进的PWM方法,分别用修正的Bootstrap方法和随机加权法对样本进行再抽样,然后根据PWM方法进行区间估计,并以潘家口水库径流量为例,对2种改进的PWM方法与传统方法进行比较,改进的PWM方法的精度更高,在相同的置信水平下,置信区间更短.
径流量;修正的Bootstrap法;随机加权法;改进的PWM法;
在数理统计中,区间估计是一个分析问题、处理问题的极其重要的方法,由于它的简单,易理解的特性,使得它在实际中也有非常广泛的应用.在大样本的情形下基于大数定理和中心极限定理的区间估计方法的理论研究和应用都已经非常成熟.但是,传统的用于大样本情形的区间估计方法在样本数量上是有一定的要求的,从而在某种程度上并不适合于小样本情形:原因是传统的区间估计方法受异常点影响较大,当样本较小时或存在异常点时,使用传统区间估计方法易导致置信区间的精度不高,不能准确地估计位置参数.
在多件情形下,样本的观测数目都是有限的.因此小样本问题越来越突出,有效的小样本区间估计在各个领域都显得非常重要.但是,前面说过,对于小样本数据,传统的区间估计方法很难或者不能取得理想的效果,在实际的应用中很难能得到我们希望的结果.因此,寻求一种与样本数目无关的区间估计方法,既能够适用于大样本情形,又能够适用于小样本情形的区间估计方法至关重要,这个问题在实际的应用中也有非常重要意义.
1 Bootstrap方法与随机加权法
1.1 修正的Bootstrap法
在统计学中,Bootstrap法[1]是指利用原始样本数据进行再抽样,得出新的样本数据及统计量的一种样本再生方法.Bootstrap方法[2]根据已经给定的原始样本数据来复制原始观测信息,该方法不需要对原始分布进行主观假设或者增加新的样本信息,就可以对总体的分布进行统计推断.
设原始样本为x1,x2,…,xn,修正的Bootstrap方法[3-4]的步骤:
1) 在内随机产生n个(0,1)内的小数ri,i=1,2,…,n,其中n为原始样本容量;
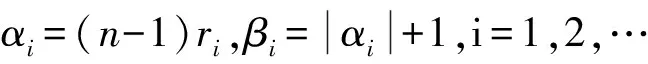
3) 以此作为一个新的样本.如此继续重复抽样B次,得到B个Bootstrap样本.
得到的新样本通过数据分析,目前还没有找到其存在的缺陷.文献[4]证实了这种抽样方法的可行性.
1.2 随机加权法(Bayesian Bootstrap)
随机加权法[5]是一种直接利用原始样本数据,借助计算技术,通过对观测数据的重新再抽样,产生原始样本的再生样本,以此来模拟总体分布.该方法的优点与Bootstrap方法类似[6-7],都不需要对未知总体分布做相关的假设,消除主观因素对于估计结果的影响.其主要思想表述如下:
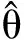
其中对于N组Diricklet随机向量的产生有[8]:
令ν(i)=(νi1,νi2,…,νin),i=1,2,…,N,
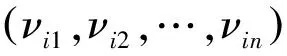
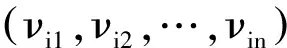
随机加权法的思想实质就是重复再抽样,对小样本数据Borel函数进行加权处理,得到其再生样本,从而获得相关的分布信息.这种方法跟Bootstrap方法是并列的,当样本量n固定时,随机加权法实际上是一种Bootstrap的极限情况.而经过初步研究分析表明:在小样本情况下,随机加权法要比Bootstrap法效果好些[5].
因此,对于修正的Bootstrap方法,考虑Bootstrap方法和随机加权法及两者的关系,对随机加权法取同样的函数,建立新的改进的PWM方法[6,9].
2 改进的PWM方法
PWM方法是一种区间预测法,结果为一个区间,从而使预测的允许范围扩大,一定程度上可满足实际的工作需要.为了准确捕捉样本的数据特征,PWM通过引进深度函数[10]及权函数[11]降低异常点的权重,缓解异常点对整体数据的影响,对数据进行特定的加工,充分利用样本数据特征从而使区间估计更具稳健性,且在相同置信水平下置信长度比其他的区间估计法更短.而改进PWM法在保留PWM优点的基础上,考虑了更全面的可能的数据情况,从而对不同的样本动态调整其权重,使预测结果更可信.
2.1 改进的PWM方法1
步骤如下:

2) 定义深度函数
PD(xi,X)=
3) 定义权函数
该权函数为负指数型权函数,其中k是正整数,c是权重的控制系数,控制着相对的权重,m为影响半径.当然也可以使用其他类型的权函数.
4) 定义深度加权平均PWM

当然,可以证明PWM具有渐进正态性[11],且有PWM(X)→u(n→∞).
5) 利用改进的Bootstrap抽样方法对原始样本进行抽样,得到B个样本,对每一个样本都按照上述步骤,得到B个PWM值:PWM1,PWM2,…,PWMB,对这B个PWM值按照小到大进行排序,得到PWM(1),PWM(2),…,PWM(B),然后按照百分位法截尾,得到置信水平为1-α的置信区间是
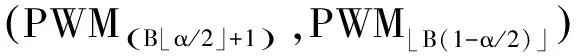
2.2 改进的PWM方法2
对于改进的PWM方法2来说,前4步同改进的PWM方法1相同,只需将其第5步修改如下:
利用随机加权法对原始样本进行抽样,得到B个样本,对每一个样本都按照上述步骤,得到B个PWM值:PWM1,PWM2,…,PWMB,对这B个PWM值按照小到大进行排序,得到PWM(1),PWM(2),…,PWM(B),然后按照百分位法截尾,得到置信水平为1-α的置信区间是

3 2种改进的PWM方法之间及与经典方法和百分位法的优良性比较
本文分别取正态总体N(0,1),泊松分布总体P(4)及指数分布总体Exp(1/4),运用Matlab软件进行模拟抽样,取出服从这3种分布的随机样本,令样本数目分别为7、10、20,并且令重抽样次数M为500.应用经典方法、百分位法以及改进的PWM方法1和改进的PWM方法2进行区间估计,程序运行一次得到的结果整理见表1.通过表1可以看出:在同一总体分布下,改进的PWM方法要比传统的百分位方法和经典方法结果更好,其精度更高,也即得到的置信区间长度更短,而相比之下,应用随机加权法的改进的PWM方法2比应用修正的Bootstrap方法的改进的PWM方法1更好,得到的置信区间平均长度最短.
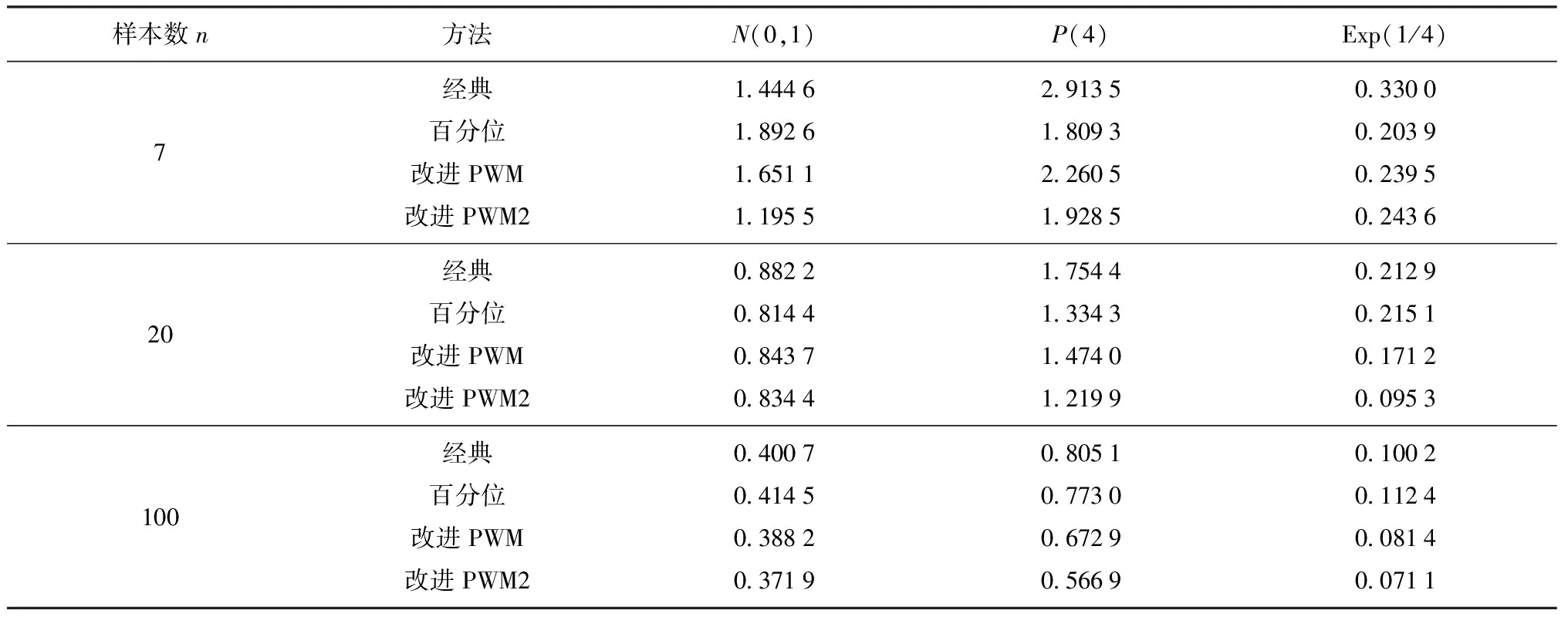
表1 4种方法下正态N(0,1)、泊松P(4)、指数Exp(1/4)分布的置信水平为95%的随机模拟500次置信区间的平均长度
4 实例分析
本文数据来自海河水利委员会的原始实测数据,使用滦河潘家口1980年至2009年30年的径流量数据,而由于时间序列的非平稳性,我们对其进行取对数并一阶差分处理.运用经典方法和百分位法以及两种改进的PWM方法对平稳后的数据进行区间估计,并对其结果进行分析.取置信水平为95%,重抽样样本数N为500,结果见表2.
由该实例我们可验证我们前面对于优良性的比较结果,改进的PWM方法要比传统的经典方法和百分位法的精度高,即其置信区间长度要小,这是由于对于小样本来说异常点的影响是非常重要的,改进的PWM方法通过取动态的权函数减弱了异常点对于整个时间序列的影响,通过取深度函数放大了对结果有益的数据的作用,这大大提升了区间估计的稳健性,对于径流量来说,它的影响因素很多,在样本数据上是有很大的随机性,很容易受到异常点的影响,因此改进的PWM方法的结果会更好一些.又由表2可知改进的PWM方法2的精度要比改进的PWM方法1要高,这也证明了我们构造改进的PWM方法2的可行性.

表2 4种方法下对平稳的潘家口径流量数据的置信水平为95%的随机模拟500次置信区间的平均长度
5 结语
影响径流量变化的因素很多,有些因素属于基本因素,它对事物的发展起决定作用,会使径流量时间序列呈现一定的规律性;有些因素是属于偶然的非基本因素,对事物的发展只起局部的非决定性作用,使径流表现出不规则的波动,出现过大或过小异常点.本文通过时原始样本进行重新抽样,构造了新的改进的PWM方法,并进行了对比.修正的Bootstrap方法本身对于小样本抽样来说已经有其非常好的性质,随机加权法与Bootstrap方法的本质是一样的,只是在其对原样本重新抽样过程中所做的处理不同,这也是今后可以进行改进的一个方向.
[1] 吴建荣. 泛函型统计量的Bootstrap与随机加权法[J].苏州大学学报:自然科学版,1992,8(3):249-254.
[2] 贾占强,蔡金燕,梁玉英. 基于改进Bootstrap和Bayesian Bootstrap的小样本产品实时性能可靠性评估[J].计算机应用研究,2009,26(8):2851-2854.
[3] 张守玉,封伟书. 基于Bootstrap方法的正态分布样本数据生成研究[J].装配指挥技术学院学报,2009,20(2):97-100.
[4] 曹欣,孙新利,李振. 改进灰自助法及其在可靠性评定中的应用[J].山东大学学报:工学版,2010,40(1):144-148.
[5] 郑忠国. 随机加权法[J].应用数学学报,1987,10(2):247-253.
[6] 刘新爱,张磊. 基于自助法和随机加权法的导弹精度评定的探讨[J].弹箭与制导学报,2006,26(1):195-197.
[7] 毛平. Bootstrap方法及其应用[D].湘潭:湘潭大学,2013.
[8] 张守玉,封伟书. 基于随机加权法的装备平均维修时间验证研究[J].装备指挥技术学院学报,2009,20(3):100-103.
[9] 张守玉,刘博强. 小样本下装备平均维修时间验前分布确定方法研究[J].装备指挥技术学院学报,2010,21(5):93-96.
[10] ZUO Yi-jun. Data depth trimming counterpart of the classical t(or T2)procedure[J]. Journal of Probability and Statistics, 2009:1-9.
[11] ZUO Yi-jun,CUI Heng-jian,HE Xu-ming.On the Stahel-Donoho estimator and depth-weighted means of multivariate data[J]. Annals of statistics, 2004:167-188.
(责任编辑 梁志茂)
Two improved PWM methods and their application to theinterval estimation for runoff
KANG Hui1,YUAN Yong-sheng1,DAI Qi-fan2
(1.College of Science,Hohai University,Nanjing 211100,China;2.Administrative Office of Irrigation Canals of Jiangsu Province,Huai′an 223200,China)
For using the improved PWM,we exponentially down-weight the abnormal points to alleviate their influence and dynamically adjust the weights to the different data to gain more robustness. Meanwhile,we get a shorter confidence interval with the improved PWM than other estimation methods.So in the condition of small sample,we can use the improved PWM method of interval estimation.The two improved PWM methodsare the random weighting method and the improved bootstrap method respectively.We take PanjiakouReservoir as an example to compare the effects of the two improved PWM methodswith those of the traditional methods. The result shows that the improved PWM methods have high precision, and the confidence interval is shorter at the same confidence level.
runoff; improved Bootstrap method;random weighting method;improved PWM method
2014-11-25.
江苏省水利科技创新基金(2011059) ; 河海大学自然科学基金(2009426311).
康慧(1990-) ,女,硕士研究生.主要研究方向:数理统计及其应用.
袁永生(1964-) ,男,教授,硕士生导师.主要研究方向:概率统计及工程中的数学问题.
O212
A
1672-8513(2015)04-0300-04
